Лабораторная по структурам и алгоритмам компьютерной обработки данных. стуктуры 5 Роговский 12002001. Институт инженерных и цифровых технологий кафедра математического и программного обеспечения информационных систем

• Название: Институт инженерных и цифровых технологий кафедра математического и программного обеспечения информационных систем
• Анкор: Лабораторная по структурам и алгоритмам компьютерной обработки данных
• Дата: 22.12.2021
• Размер: 89.58 Kb.
• Имя файла: стуктуры 5 Роговский 12002001.docx
• Тип: Отчет; #314069

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«БЕЛГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ НАЦИОНАЛЬНЫЙ

ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ»

(НИУ «БелГУ»)

ИНСТИТУТ ИНЖЕНЕРНЫХ И ЦИФРОВЫХ ТЕХНОЛОГИЙ
КАФЕДРА МАТЕМАТИЧЕСКОГО И ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ ИНФОРМАЦИОННЫХ СИСТЕМ

Структура и алгоритмы компьютерной обработки данных

Отчет по лабораторной работе №5
Студента 2 курса группы 12002001

Роговского Никиты Станиславовича

Проверила:

Черноморец Д.А.

Белгород 2021

Тема работы: Структуры данных для хранения графов

Цель: изучение основных структур данных, использующихся для хранения графов, и приобретение навыка разработки программ, преобразующих одни структуры в другие.
Вариант 3

Задание: Разработать алгоритм преобразования списка рёбер в матрицу смежности.
Теоретическая часть

Граф – это пара G=, где V – конечное непустое множество вершин, Е – множество ребер (пар вершин). Граф состоит из множества элементов данных, называемых вершинами и множества ребер, соединяющих эти вершины попарно.

Если пары Е неупорядочены – граф неориентированный, иначе – граф ориентированный (орграф). Если часть ребер ориентирована, а часть нет, то такой граф называется смешанным. Вершины V1 и V2 называются смежными, если существует ребро Е=(V1,V2), соединяющее их. Ребра называют смежными, если они имеют хотя бы одну общую вершину. Говорят, что ребро Е=(V1,V2) инцидентно вершинам V1 и V2.

Графы можно задавать в виде матрицы смежности и списка рёбер.

Матрицей смежности графа G=(V, E) называется матрица A порядка n×n, где n – количество вершин графа. Элементы матрицы смежности a_ij определяются следующим образом:

а_ij = 1, если (v_i, v_j)ÎЕ, v_i,v_jÎV;

a_ij = 0, если (v_i,v_j)ÏЕ.

Список рёбер графа — это список, в котором перечислены все рёбра графа. Элемент списка будет хранить в себе начало, конец дуги и указатель на следующее ребро:


Список рёбер
Пример орграфа, его списка рёбер и матрицы смежности: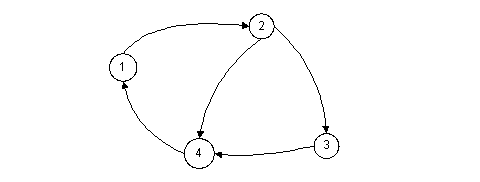


Орграф

Начало дуги	1	2	2	3	4
Конец дуги	2	3	4	4	1

Список рёбер

0	1	0	0
0	0	1	1
0	0	0	1
1	0	0	0

Матрица смежности
Практическая часть
Код программы:

#include

using namespace std;
struct EdgesListItem

{

int start, end;

EdgesListItem* next;

EdgesListItem(const int start, const int end)

{

this->start = start;

this->end = end;

this->next = nullptr;

}

};
class EdgesList

{

public:

EdgesList();

EdgesList();

void Input(const int& e);

void AddItem(EdgesListItem* const item);

void Get(int& i, int& j, EdgesListItem*& temp, const int& counter);
private:

EdgesListItem* head;

};
EdgesList::EdgesList()

{

head = nullptr;

}
EdgesList::EdgesList()

{

EdgesListItem* temp = head;

while (head != nullptr)

{

head = head->next;

delete temp;

temp = head;

}

}
void EdgesList::Input(const int& e)

{

int start, end;

EdgesListItem* item;

for (int i = 0; i < e; i++)

{

cout << "Введите начало дуги: ";

cin >> start;

cout << "Введите конец дуги: ";

cin >> end;

item = new EdgesListItem(start, end);

this->AddItem(item);

}

}
void EdgesList::AddItem(EdgesListItem* const item)

{

EdgesListItem* temp = head;

if (temp == nullptr)

head = item;

else

{

while (temp->next != nullptr)

{

temp = temp->next;

}

temp->next = item;

}

}
void EdgesList::Get(int& i, int& j, EdgesListItem*& temp, const int& counter)

{

if (i == 0)

temp = head;

if (counter > 0)

{

i = temp->start;

j = temp->end;

}

temp=temp->next;

}
class AdjacencyMatrix

{

public:

AdjacencyMatrix(int& n);

AdjacencyMatrix();

void AdjacencyMatrixFill(int& i, int& j);

void Output();

private:

int n;

int** matrix;

};
AdjacencyMatrix::AdjacencyMatrix(int& n)

{

this->n = n;

matrix = new int* [n];

for (int i = 0; i < n; i++)

matrix[i] = new int[n];
for (int i = 0; i < n; i++)

for (int j = 0; j < n; j++)

matrix[i][j] = 0;

}
AdjacencyMatrix::AdjacencyMatrix()

{

for (int i = 0; i < n; i++)

delete[] matrix[i];

delete[] matrix;

}
void AdjacencyMatrix::AdjacencyMatrixFill(int& i, int& j)

{

matrix[i - 1][j - 1] = 1;

}
Метод вывода матрицы смежности:

void AdjacencyMatrix::Output()

{

cout << endl << "Матрица смежности:" << endl;

for (int i = 0; i < n; i++)

{

for (int j = 0; j < n; j++)

{

if (j != 0)

cout << " ";

cout << matrix[i][j] << ' ';

}

cout << endl;

}

}
В главной функции программы пользователь вводит количество дуг и вершин графа, создаётся матрица смежности, происходит ввод элементов списка рёбер, после чего для перевода списка рёбер в матрицу смежности запускается цикл, по окончании которого выводится результат:

void main()

{

setlocale(LC_ALL, "Russian");

int i = 0, j = 0, n, e;

EdgesList EL;

EdgesListItem* temp;

cout << "Введите количество дуг: ";

cin >> e;

cout << "Введите количество вершин: ";

cin >> n;

int counter = e;

AdjacencyMatrix matrix(n);

EL.Input(e);

while (counter > 0)

{

EL.Get(i, j, temp, counter);

matrix.AdjacencyMatrixFill(i, j);

counter--;

}

matrix.Output();

}


Тестирование:

Пример 1:



Орграф

Начало дуги	1	2	2	3	4
Конец дуги	2	3	4	4	1

Список рёбер

0	1	0	0
0	0	1	1
0	0	0	1
1	0	0	0

Матрица смежности

Результат работы программы: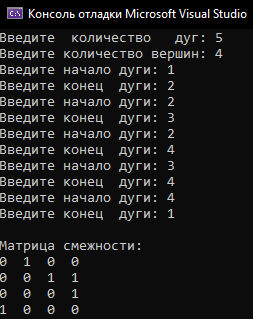


Пример 2: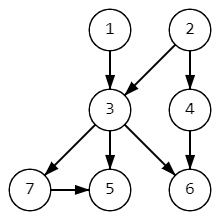



Орграф

Начало дуги	4	3	3	3	1	2	2	7
Конец дуги	6	6	5	7	3	3	4	5

Список рёбер

0	0	1	0	0	0	0
0	0	1	1	0	0	0
0	0	0	0	1	1	1
0	0	0	0	0	1	0
0	0	0	0	0	0	0
0	0	0	0	0	0	0
0	0	0	0	1	0	0

Матрица смежности

Результат работы программы: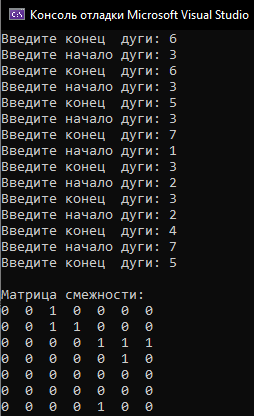