Итоговая работ 10 класс. Инструкция по выполнению итоговой диагностической работы На выполнение итоговой диагностической работы по математике дается 40 минут
 Скачать 4.54 Mb. Скачать 4.54 Mb.
|
|
Итоговая диагностическая работа по математике 10-е классы 2021-2022 учебный год Инструкция по выполнению итоговой диагностической работы На выполнение итоговой диагностической работы по математике дается 40 минут. Работа состоит из двух частей, включающих в себя 9 заданий. Часть 1 содержит 10 заданий (задания 1–7) базового уровня сложности, проверяющих наличие практических математических знаний и умений. Ответом к каждому из заданий 1–7 является целое число или конечная десятичная дробь. Часть 2 содержит два задания №8-10 – повышенного и высокого уровня сложности. При его выполнении надо записать полное решение и записать ответ. Решения и ответы заполняется яркими чёрными или синими чернилами. Допускается использование гелевой, капиллярной или перьевой ручки. При выполнении заданий Вы можете пользоваться черновиком. Обращаем Ваше внимание, что записи в черновике не будут учитываться при оценивании работы. Советуем выполнять задания в том порядке, как они даны. Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если после выполнения всей работы у Вас останется время, Вы сможете вернуться к пропущенным заданиям. Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов. Желаем успеха! Вариант 1 Часть 1
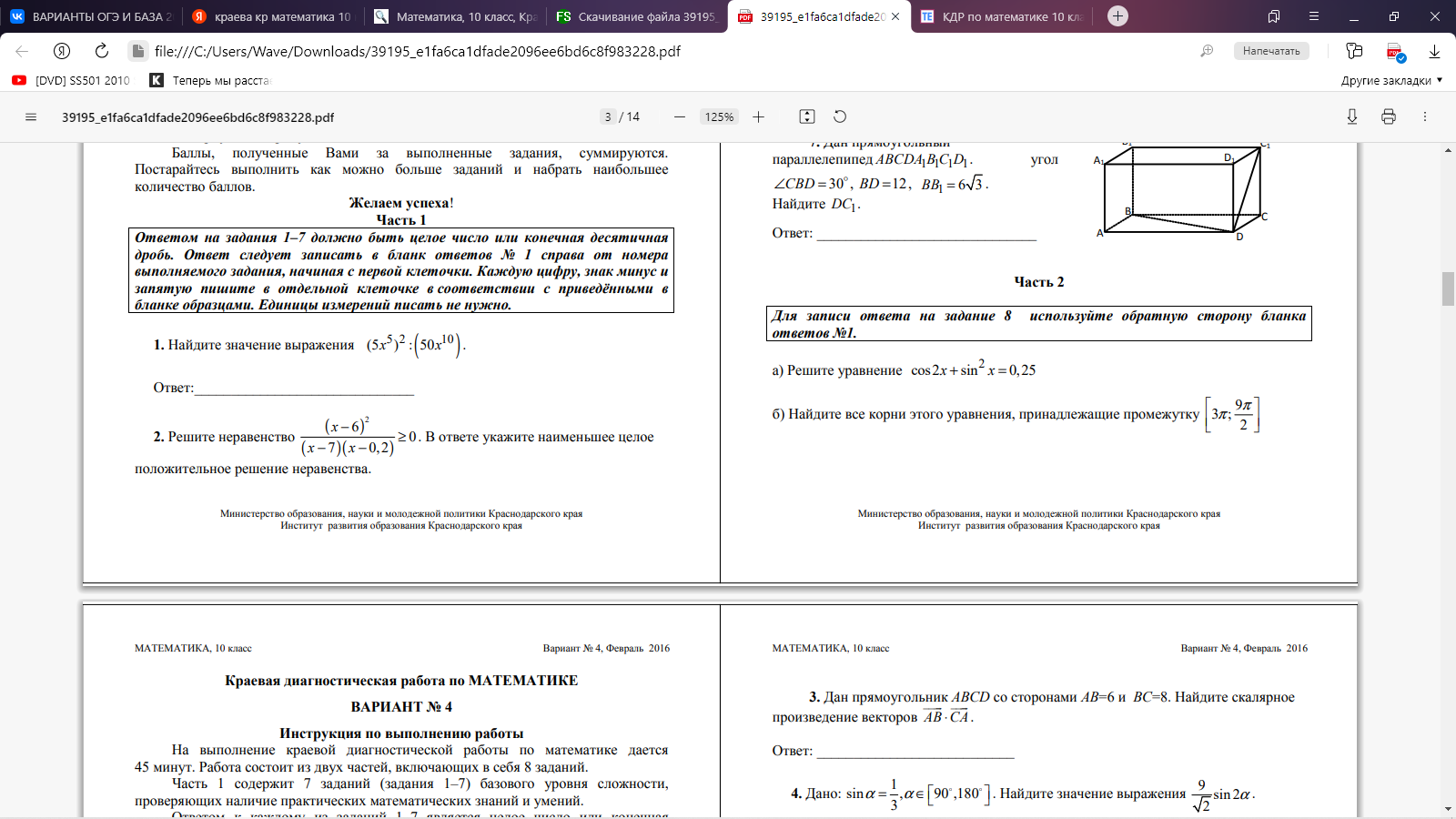  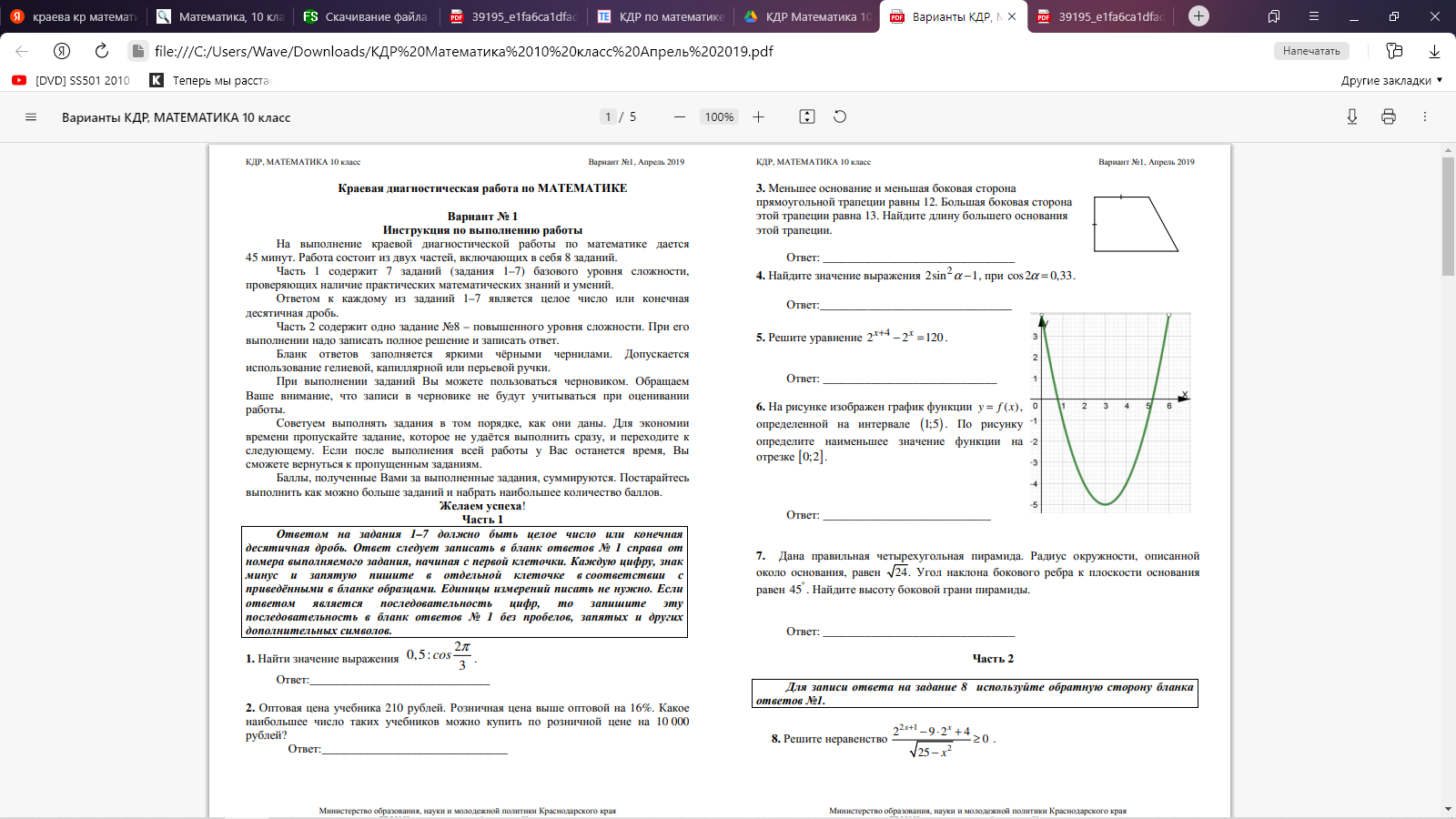 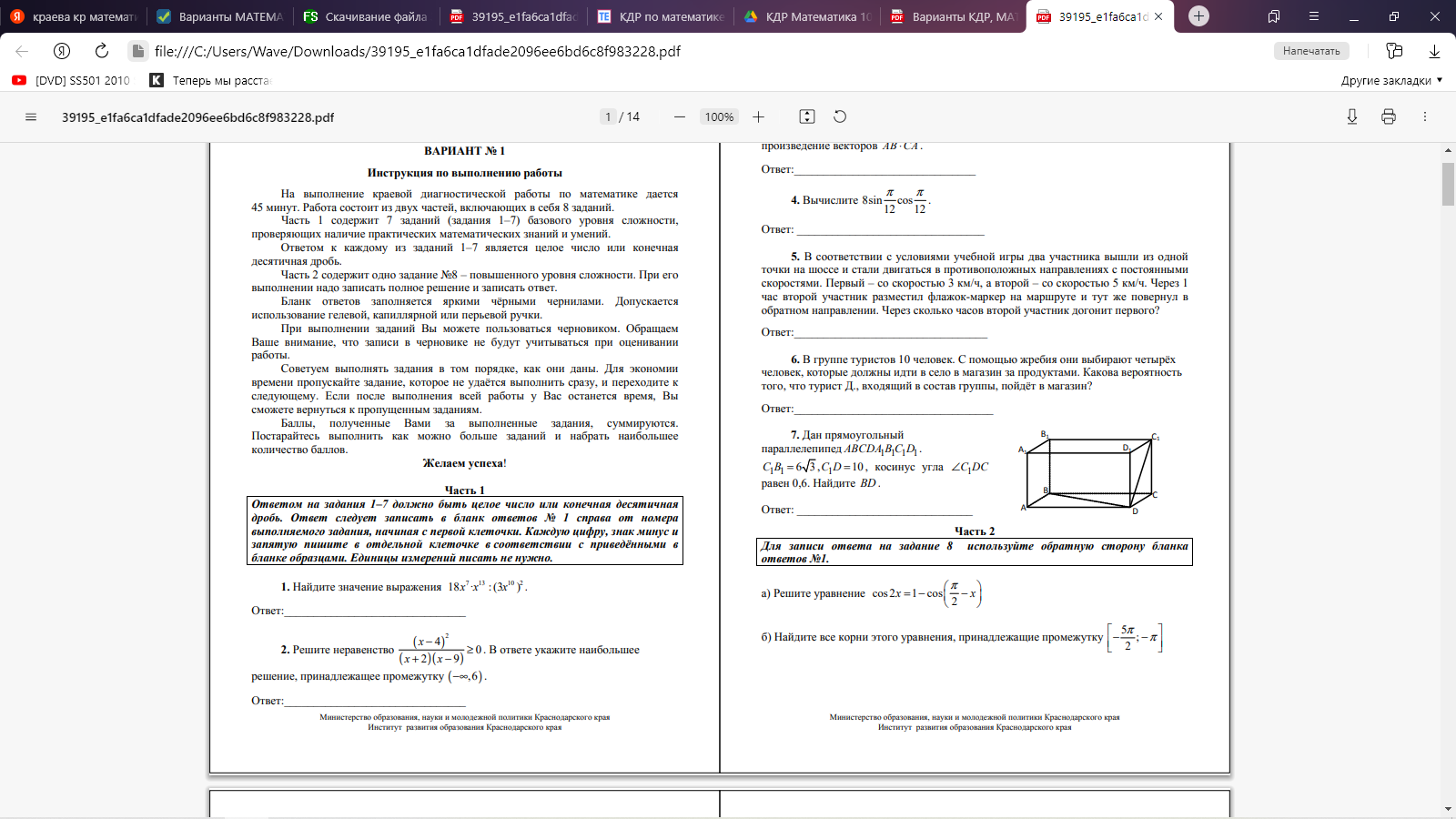 Часть 2. 8. Определите промежутки монотонности функции и характер экстремума: f(x)=x3 +x2 –x-1 9. 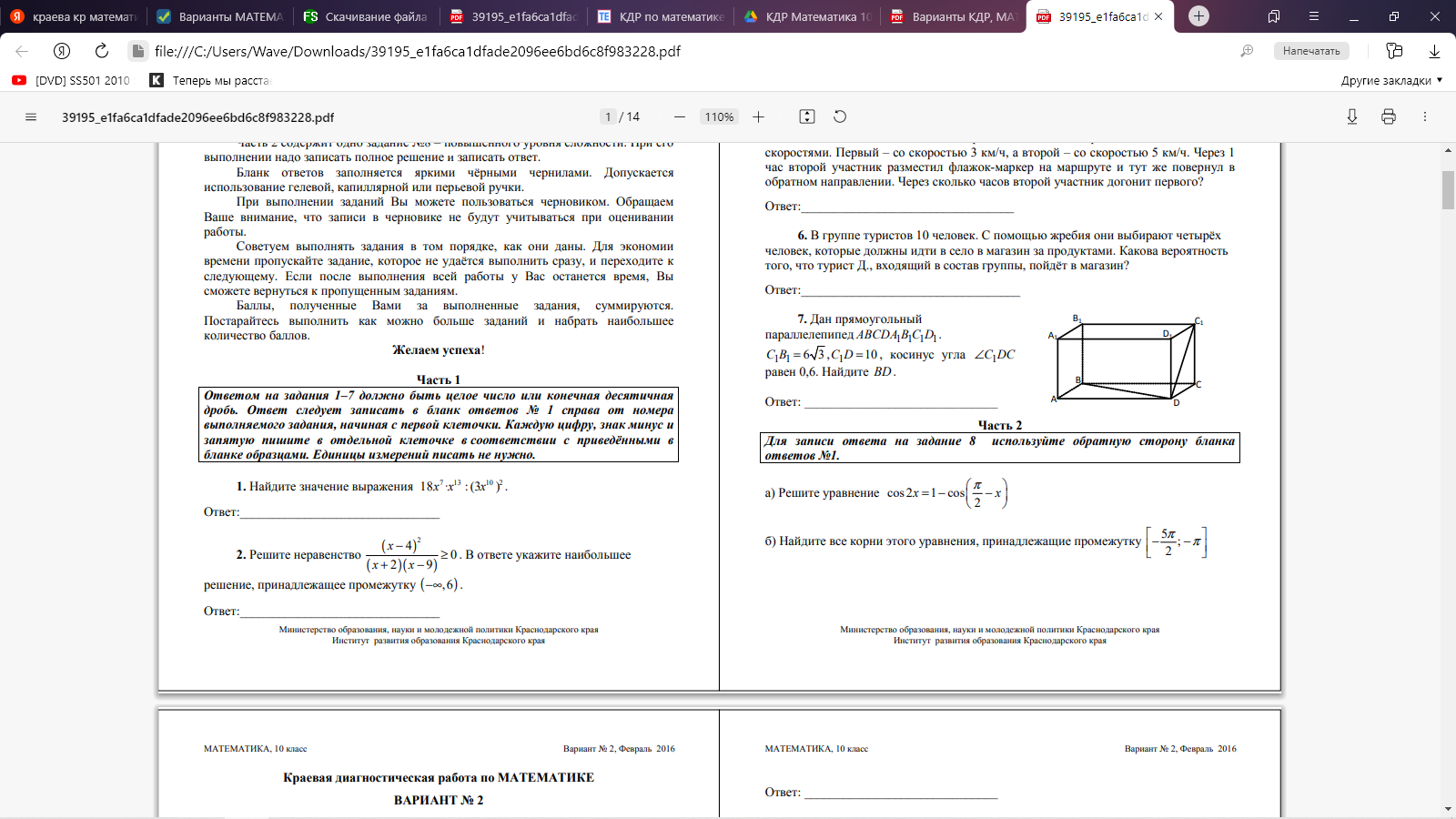 10. Дана пирамида SABC, в которой SC=SB=AB=AC= √17, SA=BC=2 √ 5 . а) Докажите, что ребро SA перпендикулярно ребру BC. б) Найдите расстояние между ребрами BC и SA. Вариант 2 Часть 1
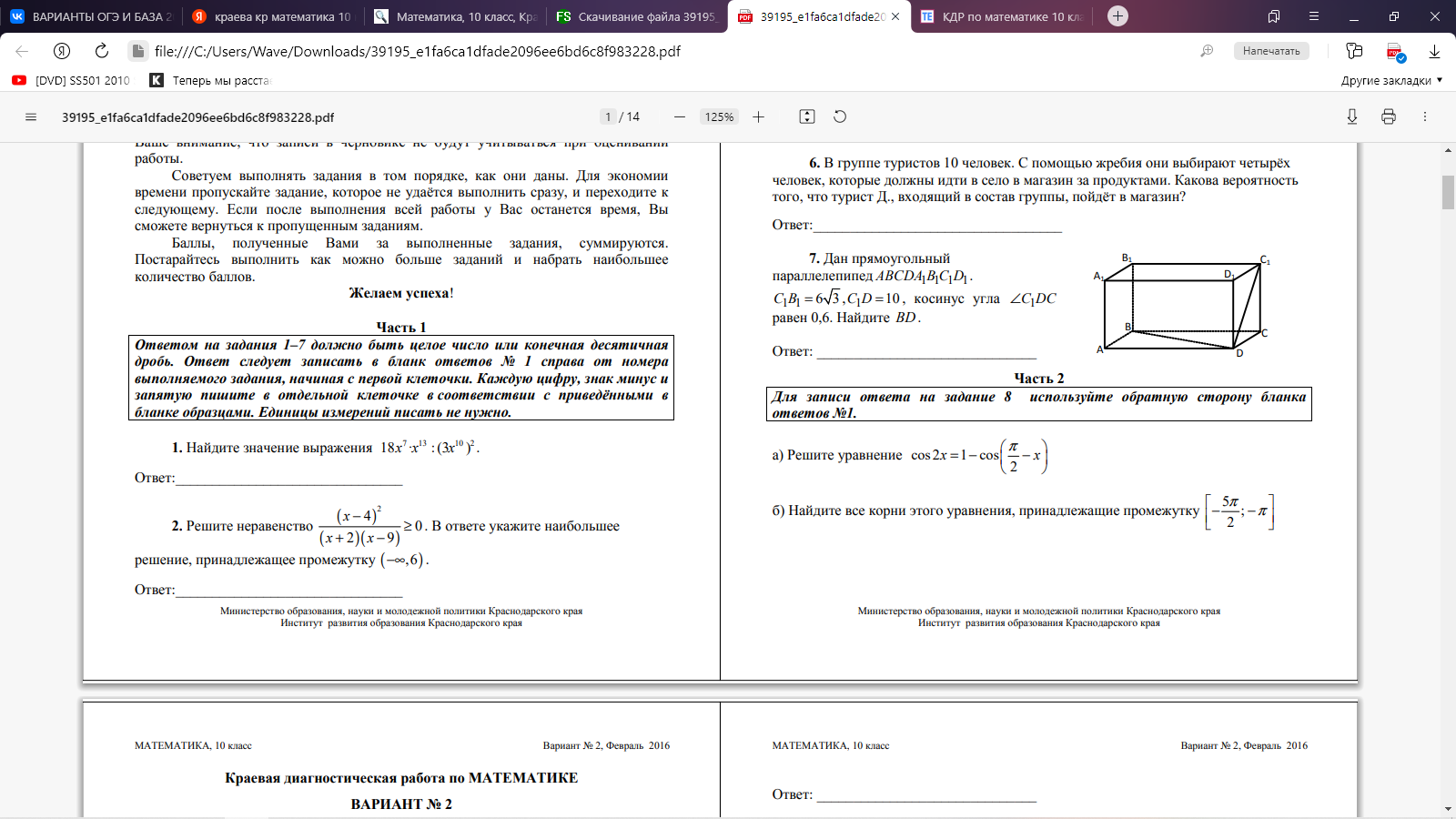  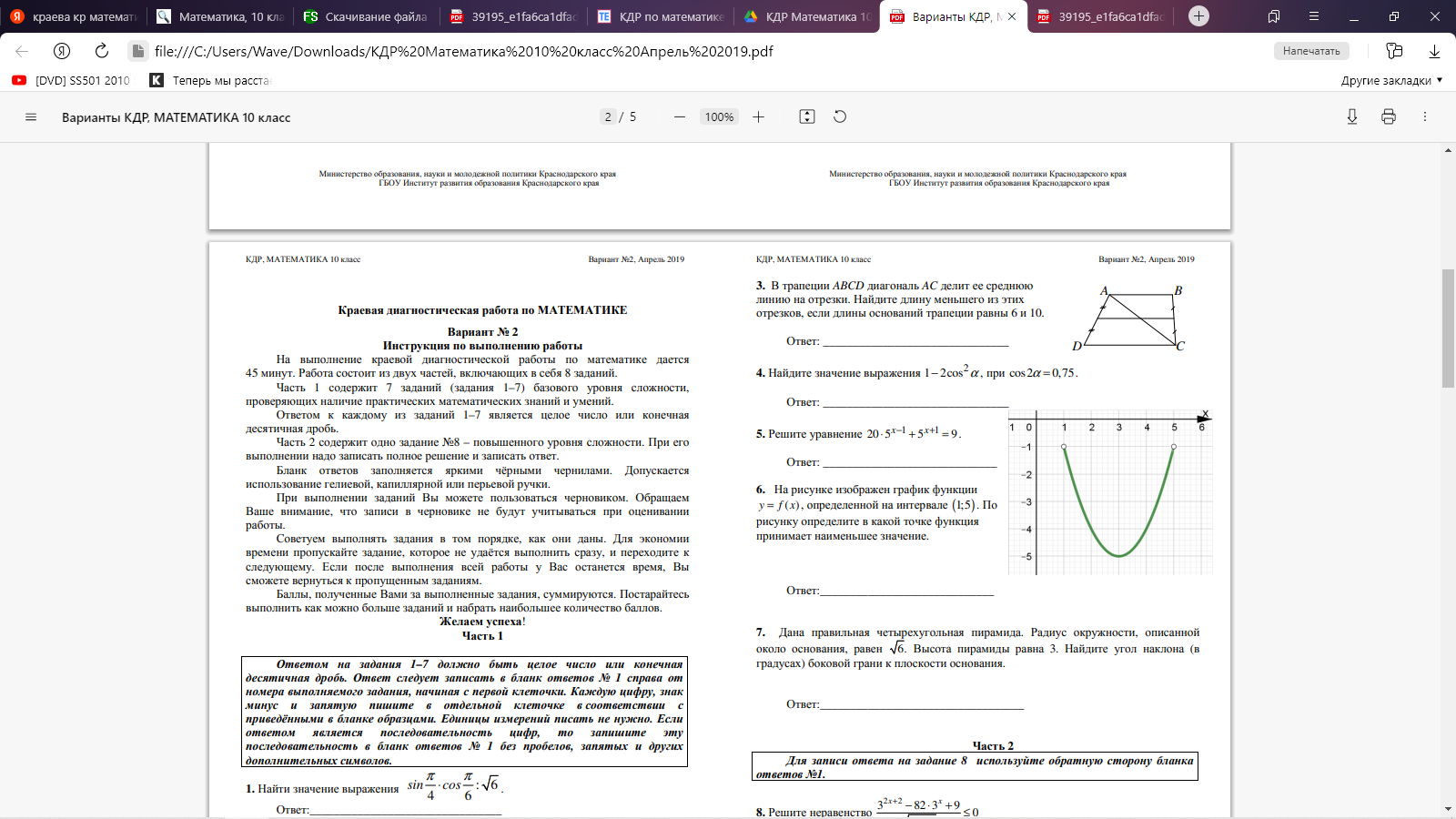 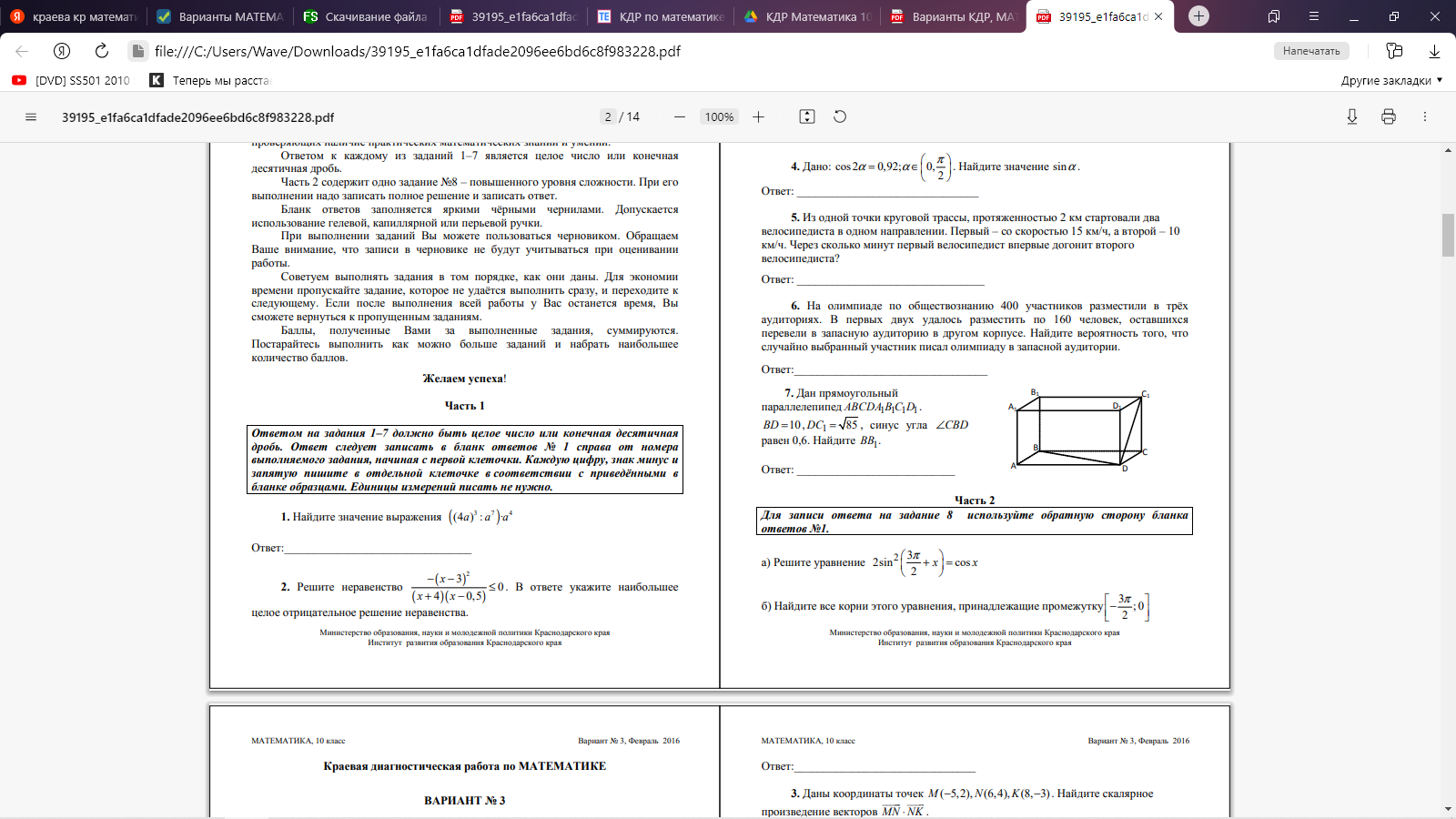 Часть 2. 8. Определите промежутки монотонности функции и характер экстремума: f(x)=-x3 +2x2 –x-1 9. 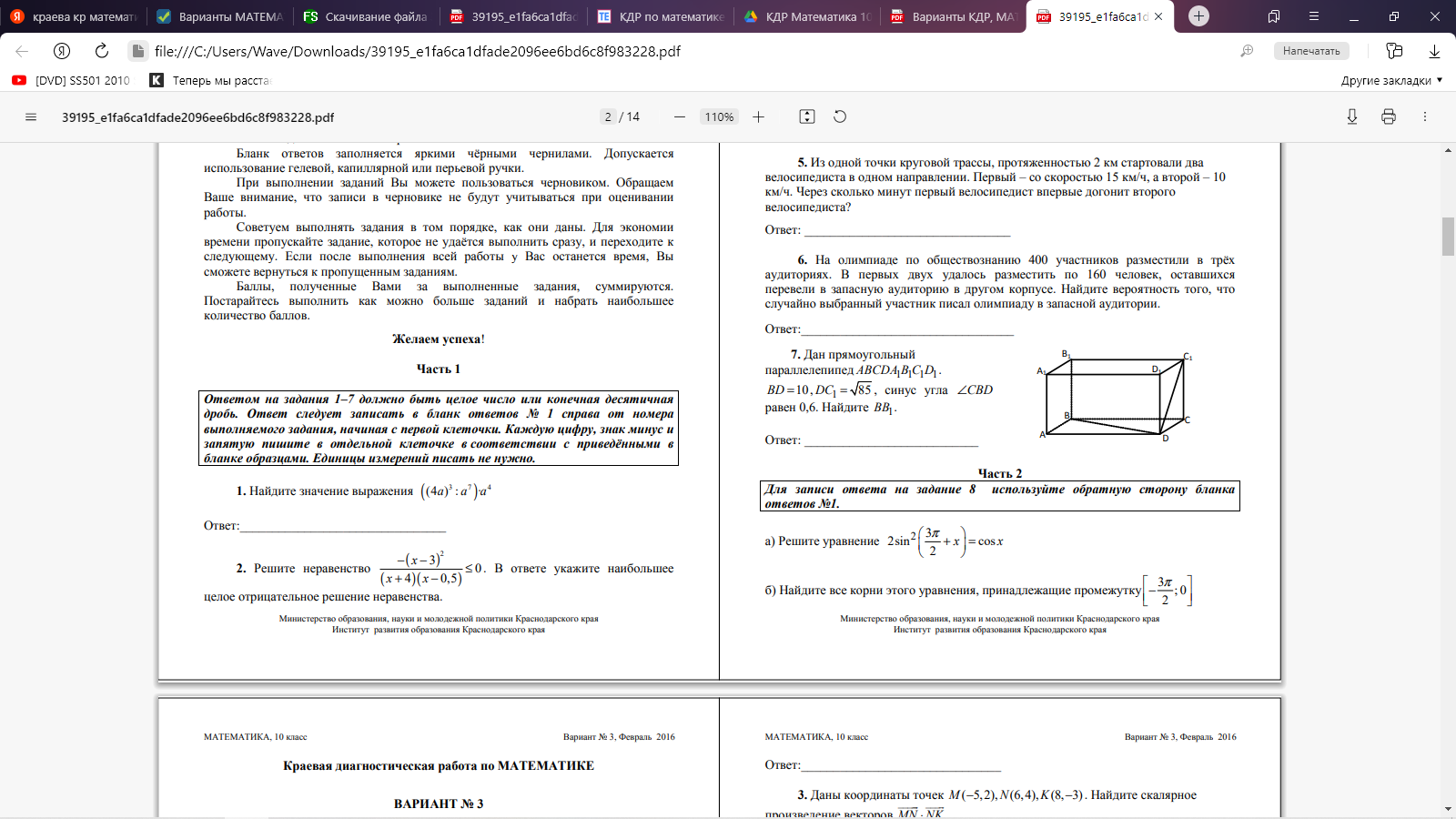 10. Дана пирамида SABC, в которой SC=SB=AB=AC= √19, SA=BC=2 √ 6 . а) Докажите, что ребро SA перпендикулярно ребру BC. б) Найдите расстояние между ребрами BC и SA. Вариант 3 Часть 1
  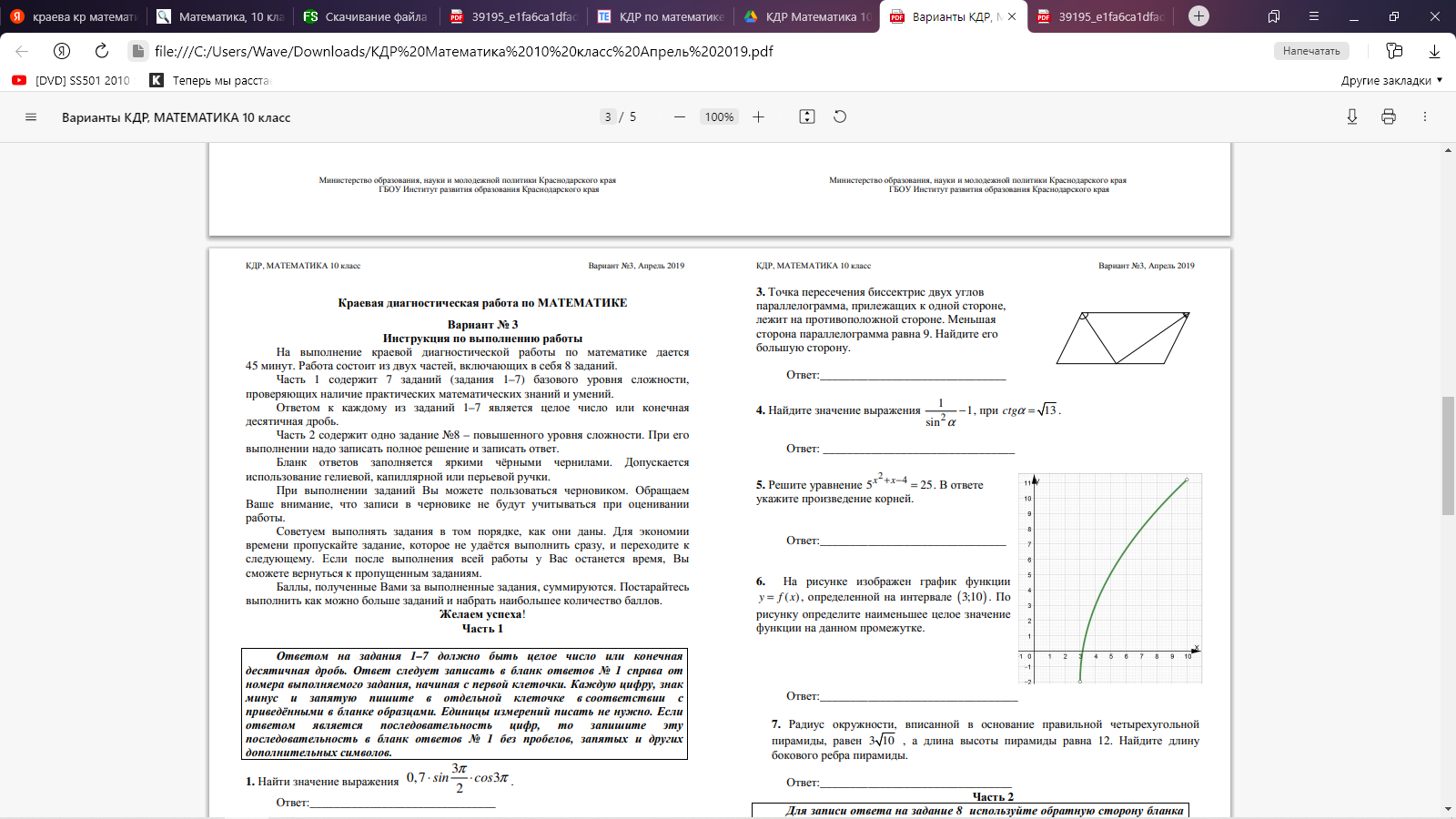 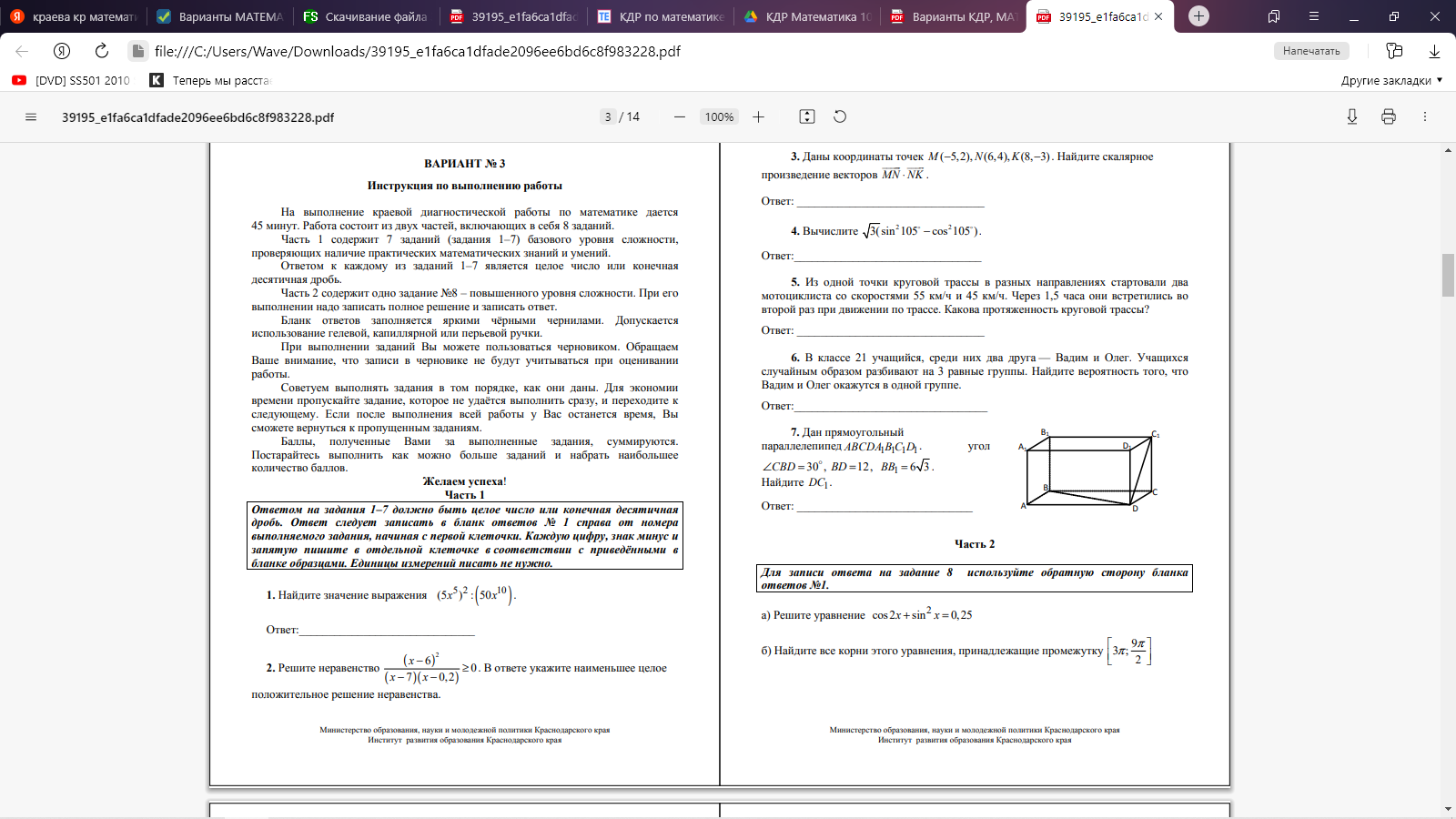 Часть 2. 8. Определите промежутки монотонности функции и характер экстремума: f(x)=2x3 +x2 –4x-1 9. 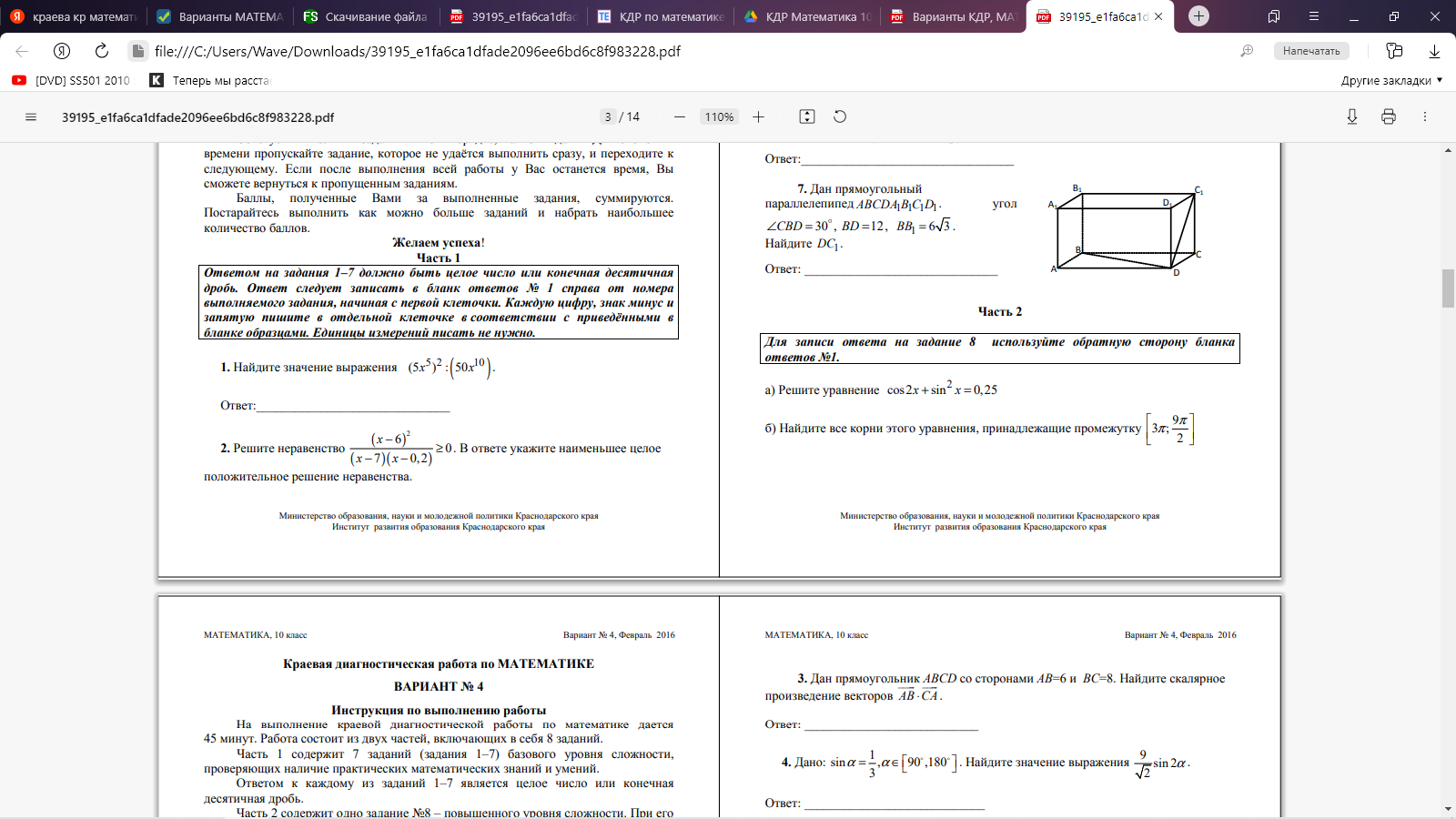 10. Все рёбра правильной треугольной призмы ABCA1B1C1 имеют длину 6. Точки M и N— середины рёбер AA1 и A1C1 соответственно. а) Докажите, что прямые BM и MN перпендикулярны. б) Найдите угол между плоскостями BMN и ABB1. Вариант 4 Часть 1
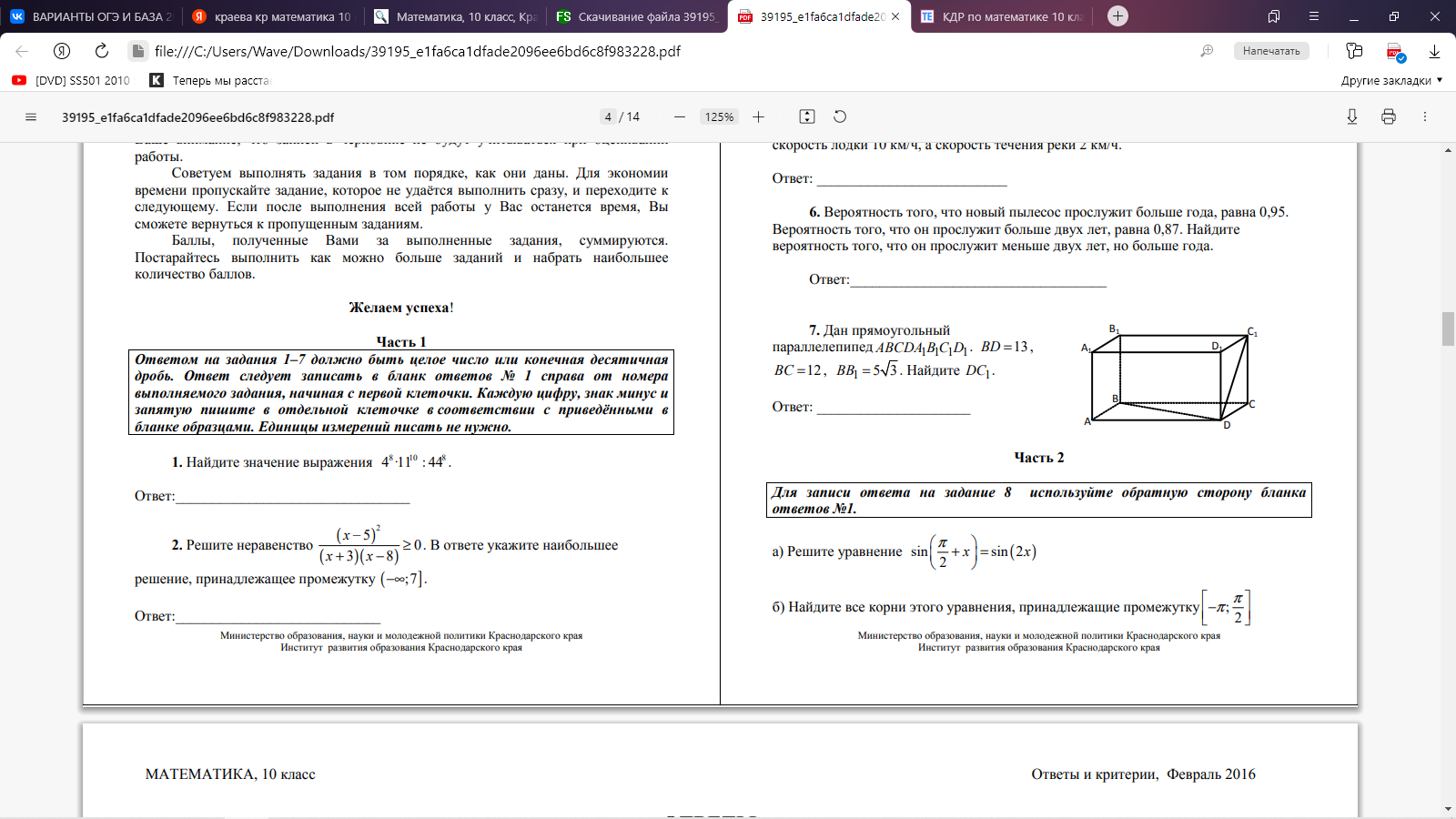    Часть 2. 8. Определите промежутки монотонности функции и характер экстремума: f(x)= -2x3 -x2 +4x-1 9.  10. Все рёбра правильной треугольной призмы ABCA1B1C1 имеют длину 12. Точки M и N— середины рёбер AA1 и A1C1 соответственно. а) Докажите, что прямые BM и MN перпендикулярны. б) Найдите угол между плоскостями BMN и ABB1. Вариант 5* Часть 1
 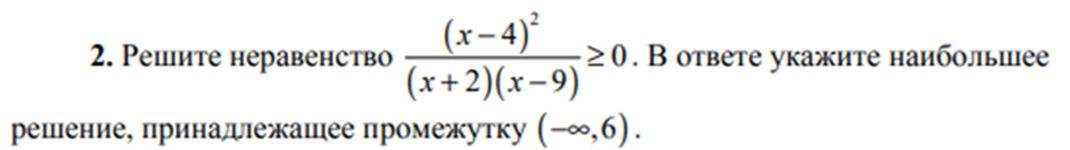   Часть 2. 8. Определите промежутки монотонности функции и характер экстремума: f(x)= -2x3 -x2 +4x-1 9. 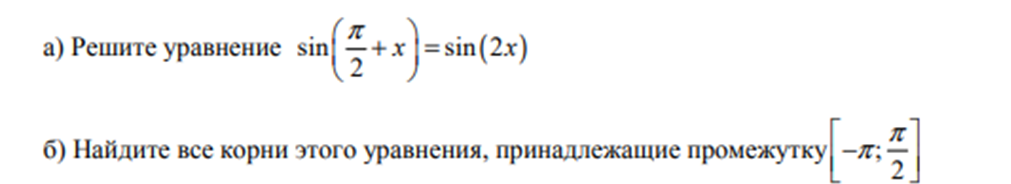 Ответы
КРИТЕРИИ ОЦЕНИВАНИЯ Max=13 1-4 – оценка 2 5-6 –оценка 3 7-9- оценка 4 10-13- оценка 5 |
