Шеркунов лабораторная 1. Инструкция пользователя 5

Название	Инструкция пользователя 5
Дата	19.01.2023
Размер	122.34 Kb.
Формат файла
Имя файла	Шеркунов лабораторная 1.docx
Тип	Инструкция #895301

Министерство науки и высшего образования Российской Федерации

Федеральное государственное автономное образовательное учреждение

высшего образования

«Уральский федеральный университет имени первого Президента России Б.Н.Ельцина»

Институт радиоэлектроники и информационных технологий – РТФ

Анализ сложности алгоритмов сортировки строк

Отчёт по лабораторной работе

по дисциплине «Алгоритмы, структуры данных и анализ сложности»

Вариант 3

Выполнил: Шеркунов Е.Г.

Студент группы: РИ-300015

Преподаватель: доцент, к.ф.-м.н. Трофимов С. П.

2022

Задание

Реализовать алгоритм сортировки строк:

3. SortTree

Выбор алгоритма по номеру в группе:
№=(V-1)%8+1 = (27 - 1)%8+1 = 3

Для алгоритма определить сложность относительно наиболее характерной операции (сравнение, перестановка и др.). Вид функции сложности F(n) подобрать в соответствии с теорией. Найти также коэффициент пропорциональности C. Для аппроксимации можно использовать метод наименьших квадратов и сервис «Поиск решения».

План проведения эксперимента с алгоритмом называется массовой задачей. Представьте план в виде xml-файла.

Результаты решения массовой задачи записать в текстовый файл в 2 столбика: длина массива, количество операций. Файл импортировать в Excel. В «шапке» листа указать параметры тренда, вычислить квадратичные невязки и минимизировать их сумму с помощью «Данные-Поиск решения»

Теоретическая часть

Основная идея заключается в построении бинарного дерева поиска из элементов массива с последующей распечаткой отсортированного массива путём обхода узлов построенного дерева.

В качестве вершины дерева выбирается первый элемент массива. Бинарное дерево строится так, чтобы левый потомок был меньше родителя, а правый потомок – больше или равен родителя. Распечатка дерева проходит рекурсивно. Начинается с вершины дерева. Сначала печатаем левое поддерево, затем вершина, затем правое поддерево.

Особенности алгоритма:

1.Процедура добавления объекта в бинарное дерево имеет среднюю алгоритмическую сложность порядка O(log(n)). Соответственно, для n объектов сложность будет составлять O(n*log(n)), что относит сортировку с помощью двоичного дерева к группе «быстрых сортировок». Однако, сложность добавления объекта в разбалансированное дерево может достигать O(n), что может привести к общей сложности порядка O(n²).

2.Требует не менее чем 4n ячеек дополнительной памяти (каждый узел должен содержать ссылки на элемент исходного массива, на родительский элемент, на левый и правый лист), однако, существуют способы уменьшить требуемую дополнительную память.

3.Использует операцию сравнения.

Инструкция пользователя

При запуске программы создается в рабочей директории results.xls файл. В нём создаются два столбца, разделенных одной табуляцией: «Длина массива» и «Количество операций». Первая строка – их наименование, последующие - целые числа. Целые числа в столбце «Длина массива» создаются с помощью массивов, заполненных случайными числами, свойства массивов задаются в .xml файле. В столбце «Количество операций» числа создаются исходя из работы алгоритма «SortTree», они равны счетчику самой частой операции, либо количеству swap-ов, либо количеству ветвлений. В этой работе будем считать количество сравнений.

Инструкция программиста

В программе, написанной на языке C#, алгоритм сортировки представлен в классе Tree. Для его реализации была написана функция Sort:

public static Tuple, int> Sort(IEnumerable items)

принимающая массив перечисляемых эелементов и сортирующая его алгоритмом SortTree. Для возможности оценивать производительность сортировки функция возвращает значение счётчика той операций, которая вызывалась чаще всего.

Количество сравнений для конкретного узла хранится в отдельной переменной переменной:

public int CompNumber
Для формирования дерева используется функция Insert:

public void Insert(T value)
Функция GetExperimentResults:

private static void GetExperimentResults()

выполняющая экспериментальные вычисления и создает .txt файл.

GetOperationsCount:

private static int GetOperationsCount(int minElement, int maxElement, int repeatsCount, int arrayLength)

принимающая параметры для создания массивов строк (их длину, диапазон значений элементов, количество массивов); она формирует массивы, запускает функцию сортировки для них и возвращает счётчик самой часто вызываемой операции.

Тестирование

Кроме основных и вспомогательных, программа также содержит функцию Test. Она содержит тесты, проверяющие корректность работы алгоритма сортировки и выполняется в момент запуска программы. Если один или несколько тестов завершились неудачно, на консоль будут выведены соответствующие сообщения, и программа завершит работу. Часть кода тестов представлена ниже, с полным кодом можно ознакомиться в Приложении.

Рисунок 1 – Часть кода тестирующей функции Test

Помимо тестирования, программа предоставляет возможность провести эксперимент с SortTree сортировкой на больших массивах данных. Для этого в xml-файле Experiment был создан план эксперимента. Он включает в себя несколько элементов nodes, каждый из которых описывает свою часть эксперимента: какое количество массивов будет сгенерировано, какой длины, с какими значениями и по какому принципу эти массивы будут изменяться (здесь реализовано изменения длины массива в арифметической и геометрической прогрессиях).

Данный документ обрабатывается в функции GetExperimentResults: значения атрибутов каждого элемента эксперимента будут получены и использованы для генерации массивов (все значения их элементов выбираются случайным образом из заданного диапазона) и последующей сортировки.

Полученные результаты (длины массивов и кол-во операций для их сортировки) заносятся в results.xls файл. В добавление к ним рассчитываем также значения тренда для каждого случая и строим графики функции сложности. Скорее всего, они будут отстоять далеко друг от друга, поэтому для их сближения применим метод наименьших квадратов: рассчитываем для каждого случая квадратичные невязки, а затем получим коэффициент для функции сложности с помощью сервиса Excel «Поиск решения».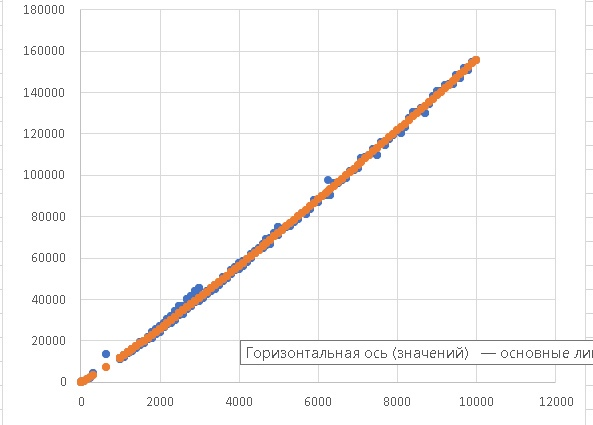

Рисунок 2 – Графики функции сложности после применения сервиса «Поиск решения»
В нашем случае для сортировки SortTree строк мы получаем коэффициенты пропорциональности a = 3,88805955137016, b = 0, c = 1,99992355295243 а функция сложности для данного алгоритма принимает вид F(n) = a * n * log(n) + b * n + c

Выводы

В данной работе мы познакомились с одним из алгоритмов сортировки – сортировкой SortTree, написали программу для сортировки массивов строк с его использованием, а также провели эксперимент для оценки сложности данного алгоритма. Полученная программа работает исправно и позволяет достаточно быстро сортировать массивы из тысяч строк. Это же подтверждается и результатами эксперимента: алгоритм имеет сложность вида O (n * log(n)).

Всё это говорит о том, что SortTree сортировка является одной из самых эффективных для сортировки большого объёма данных, однако алгоритм также имеет и недостатки, например неустойчивость и выигрыш в производительности только на больших значениях n. Таким образом, в определённых ситуациях целесообразнее использовать другие алгоритмы сортировки, более эффективные для выбранной задачи.

Литература

Федоряева Т. И. Комбинаторные алгоритмы: Учебное пособие /Новосиб. гос. ун-т. Новосибирск, 2011. 118 с.
Материалы курса «Алгоритмы и структуры данных» в УрФУ

https://www.geeksforgeeks.org/tree-sort/ SortTree

4) Котеров Д. В. и Костарев А. Ф. PHP 5 / 2008. 1094 с.

Приложение

Код классов Program и Tree:

class Program

{

private static bool Test()

{

var isAllTestsCompleted = true;

{

var startarray = new[] {10, 9, 8, 7, 6, 5, 4};

var expectedarray = new[] {4, 5, 6, 7, 8, 9, 10};

var sortedatarray = Tree.Sort(startarray);
if (!Enumerable.SequenceEqual(sortedatarray.Item1, expectedarray))

{

Console.WriteLine("Test1 wasn't passed");

isAllTestsCompleted = false;

}

}

{

var startarray = new[] {273, 89, 400, 121, 83, 340};

var expectedarray = new[] {83, 89, 121, 273, 340, 400};

var sortedatarray = Tree.Sort(startarray);
if (!Enumerable.SequenceEqual(sortedatarray.Item1, expectedarray))

{

Console.WriteLine("Test2 wasn't passed");

isAllTestsCompleted = false;

}

}

{

var startarray = new[] {"bdg", "avc", "hdf", "dg", "aa", "chd"};

var expectedarray = new[] {"aa", "avc", "bdg", "chd", "dg", "hdf"};

var sortedatarray = Tree.Sort(startarray);
if (!Enumerable.SequenceEqual(sortedatarray.Item1, expectedarray))

{

Console.WriteLine("Test1 wasn't passed");

isAllTestsCompleted = false;

}

}
return isAllTestsCompleted;

}

static void Main()

{

//Console.WriteLine(Test());

GetExperimentResults();

Console.ReadKey();

}
private static int GetOperationsCount(int minElement, int maxElement, int repeatsCount, int arrayLength)

{

var operationsCount = 0;

for (var i = 0; i < repeatsCount; i++)

{

var array = new int[arrayLength];

var random = new Random();

for (var j = 0; j < array.Length; j++)

array[j] = random.Next(minElement, maxElement);

operationsCount += Tree.Sort(array).Item2;

}
return operationsCount;

}

private static void GetExperimentResults()

{

var xDoc = new XmlDocument();

var out_csv = new StringBuilder();

xDoc.Load(Path.Combine(Environment.CurrentDirectory, "Experiment.xml"));

var xRoot = xDoc.DocumentElement;

var experiment = xRoot.SelectSingleNode("experiment");

foreach (XmlNode node in experiment.ChildNodes)

{

var minElement =

int.Parse(node.SelectSingleNode("@minElement").Value); // Получение значений атрибутов каждого node

var maxElement = int.Parse(node.SelectSingleNode("@maxElement").Value);

var startLength = int.Parse(node.SelectSingleNode("@startLength").Value);

var maxLength = int.Parse(node.SelectSingleNode("@maxLength").Value);

var repeat = int.Parse(node.SelectSingleNode("@repeat").Value);

var name = node.SelectSingleNode("@name").Value;

if (name == "Arithmetic Progression")

{

var diff = int.Parse(node.SelectSingleNode("@diff").Value);

Console.WriteLine("Эксперимент: " + name);

for (var length = startLength; length <= maxLength; length += diff)

{

var compareCount = GetOperationsCount(minElement, maxElement, repeat, length) / repeat;

var arrLength = length;

out_csv.AppendLine(string.Format("{0} \t {1}", arrLength, compareCount));

Console.WriteLine("Длинамассива: " + length + "\t" + "Кол-вомассивов: " + repeat + "\t" +

"Операцийвсреднем: " + compareCount);

}

}
if (name == "Geometric Progression")

{

var znamen = double.Parse(node.SelectSingleNode("@Znamen").Value);

Console.WriteLine("Эксперимент: " + name);

for (var length = startLength; length <= maxLength; length = (int)Math.Round(length * znamen))

{

var compareCount = GetOperationsCount(minElement, maxElement, repeat, length) / repeat;

var arrLength = length;

out_csv.AppendLine(string.Format("{0} \t {1}", arrLength, compareCount));

Console.WriteLine("Длинамассива: " + length + "\t" + "Кол-вомассивов: " + repeat + "\t" +

"Операцийвсреднем: " + compareCount);

}

}
File.AppendAllText(Path.Combine(Environment.CurrentDirectory, "report.txt"), out_csv.ToString());

Console.WriteLine("\n");

}

}

}

public class Tree where T : IComparable

{

public T Value;

public Tree Left, Right;

public int CompNumber;

public Tree()

{

Value = default(T);

Left = Right = null;

}
public void Insert(T value)

{

if (Value == null || Value.Equals(default(T)))

{

Value = value;

}

else if (value.CompareTo(Value) <= 0)

{

if (Left == null)

Left = new Tree();

CompNumber++;

Left.Insert(value);

}

else

{

if (Right == null)

Right = new Tree();

CompNumber++;

Right.Insert(value);

}

}
public void GetItems(List destinationCollection, List CompareCount)

{

if (Left != null)

{

Left.GetItems(destinationCollection, CompareCount);

}

destinationCollection.Add(Value);

CompareCount.Add(CompNumber);

if (Right != null)

{

Right.GetItems(destinationCollection, CompareCount);

}

}
public static Tuple, int> Sort(IEnumerable items)

{

var tree = new Tree();

foreach (var item in items)

tree.Insert(item);

var list = new List();

var CompareCount = new List();

int totalCompareCount = 0;

tree.GetItems(list, CompareCount);

foreach (var compares in CompareCount)

totalCompareCount += compares;

return new Tuple, int>(list, totalCompareCount);

}

}

Содержимое xml-файла Experiment: