Курсовая инвестиции. Курсовая Инвестиции. Инвестиционный портфель и портфельное инвестирование
 Скачать 109.25 Kb. Скачать 109.25 Kb.
|
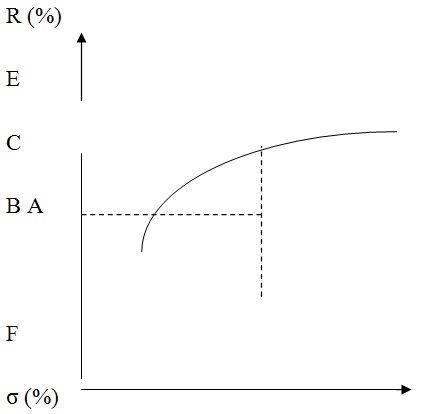 Рисунок 1 – Кривая эффективных портфелей [3, с.375]. Согласно трактовке Марковица, если имеется некий портфель А, то он является субоптимальным или неэффетивным, так как портфель В мог бы обеспечить тот же самый уровень ожидаемой доходности с меньшей степенью риска, в то время как портфель С при той же степени риска мог бы обеспечить более высокую ожидаемую доходность. Таким образом, все эффективные портфели должны лежать на кривой EF, которая часто называется «эффективной границей Марковица». Портфели, которые лежат в средней части кривой, обычно содержат много ценных бумаг, в то время как ближе к краям всего несколько. Точка F ассоциируется с тем, что все инвестиции вложены в акции одного вида, с максимальной ожидаемой доходностью. А точка Е соответствует тому положению, когда сочетание нескольких акций в портфеле обеспечивает наименьшую степень риска портфеля. Итак, модель Марковица не дает возможности выбрать оптимальный портфель, а определяет лишь набор эффективных портфелей. Каждый из этих портфелей обеспечивает наибольшую ожидаемую доходность для определенного уровня риска. Купить все эффективные портфели не представляется возможным. Кроме того, сформированный однажды эффективный портфель не остается таким постоянно, поэтому его приходится постоянно пересматривать. Ценные бумаги, входящие в портфель инвестора, можно разделить условно на две группы. В первую группу войдут ценные бумаги, имеющие малый риск и умеренную доходность. Во вторую группу войдут ценные бумаги, имеющие большую доходность и соответственно больший риск. Подход Г. Марковица предполагает, что все инвестиции вложены в рисковые активы. Теперь предположим, что инвестору разрешается вкладывать средства в безрисковые активы, т. е. если имеется N активов, то (N-1) – это количество рисковых активов и один безрисковый. Допустим также, что инвестор может привлекать займы по безрисковой ставке и использовать их для вложения в рисковые активы. Под безрисковым активом понимается актив, по которому доход является строго определенным. По определению стандартное отклонение по безрисковому активу равно нулю. Следовательно, ковариация между доходностями безрискового актива и любого рискового актива равна нулю. В качестве безрискового актива должен выступать актив, имеющий фиксированный доход и нулевую вероятность неуплаты. К таким активам могут быть отнесены государственные краткосрочные облигации, срок погашения которых совпадает с периодом владения. Покупка безрискового актива представляет собой безрисковое кредитование, так как при этом инвестор предоставляет деньги взаймы. Предположим, что инвестор выбирает портфель, составленный из рисковых активов, и намеревается комбинировать этот портфель с вложением части средств в безрисковый актив. На рисунке 2 представлен график, который сочетает рисковые и безрисковые активы. [3, с. 378]. Портфель, формируемый включением актива в рисковый портфель, должен лежать на прямой, которая соединяет точку соответствующего безрискового актива (Rf) с точкой, характеризующей портфель, составленной из определенного сочетания ценных бумаг (D). Эта прямая представляет собой комбинации портфелей, состоящих из различных долей безрискового и рискового активов. Предположим, что инвестор может увеличить свой капитал для вложения в данные бумаги за счет безрисковых займов. В частности, можно предположить, что эти займы привлекаются за счет кредита брокера. Для целей настоящего анализа предпологается, что процентная ставка по привлечению кредитных средств равна процентной ставке по безрисковым вложениям. 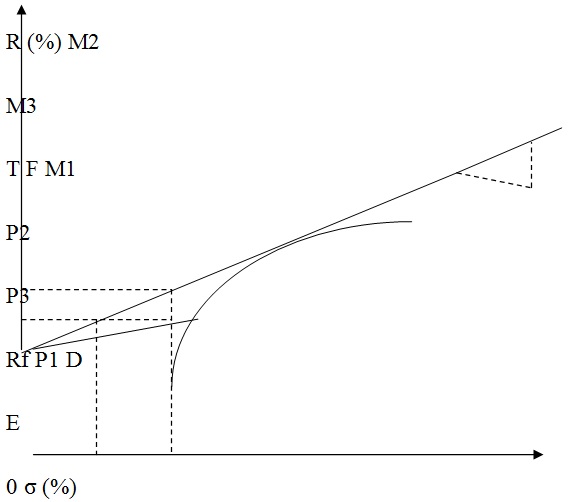 Рисунок 2 - График портфелей, сочетающих рисковые и безрисковые активы [3, с. 378]. Если доля в рисковые активы составляет WR и безрисковый заем WF, то: WR + WF = 1,2 + (-0,2) = 1 (2), [3, с. 379]. Нетрудно доказать, что портфели, состоящие из безрисковых займов и рисковых активов, будут лежать на продолжении прямой линии RfT, как и портфели, которые включали безрисковое кредитование. При этом, чем больше сумма привлеченных средств, тем выше и правее располагается точка портфеля. Точное расположение каждой точки зависит от величины займа. Какое бы количество средств мы не привлекали, если эти средства вместе с собственным капиталом помещаются в рисковый портфель, то он будет лежать на прямой RfT. Эта прямая будет представлять собой не что иное, как эффективное множество, т.е. портфели, предлагающие наилучшие возможности, будут располагаться именно на этой прямой, так как каждый из них лежит левее и выше остальных. Портфелей, лежащих влево от прямой, не существует, а любому портфелю, лежащему вправо от прямой, например портфелю М1, может быть противопоставлен портфель М3, который имеет такую же доходность, но меньшее стандартное отклонение, или портфель М2, обеспечивающий более высокую доходность при том же стандартном отклонении. Таким образом, если мы вводим условие, что инвестор имеет возможность предоставлять или получать безрисковые займы, то при этом условии ни один из портфелей, кроме портфеля Т, не является эффективным. Эффективным портфелем в эффективном множестве модели Марковица является единственный портфель Т, который находится в точке касания прямой и эффективной границы модели Марковица. Любая другая структура портфеля с использованием займов и кредитов не будет являться эффективной, так как любой из этих портфелей будет лежать правее линии RfT, а это означает, что всегда найдется портфель, который лежит на прямой. [3, с. 379-380]. Как было сказано выше, модель Г. Марковица не дает возможности выбрать оптимальный портфель, а определяет набор эффективных портфелей. Главным недостатком данной модели является то, что она требует очень большого количества информации. Гораздо меньше информации используется в модели У. Шарпа. Модель Шарпа можно считать упрощенной версией модели Марковица. Если модель Марковица можно назвать мультииндексной, то модель Шарпа называют диагональной моделью или моделью единичного индекса. [3, с.380] Согласно У. Шарпу, прибыль на каждую отдельную акцию строго корректирует с общим рыночным индексом, что значительно упрощает процедуру нахождения эффективного портфеля. Применение модели Шарпа требует значительно меньшего количества вычислений, поэтому она оказалась более пригодной для практического использования. Анализируя поведение акций на рынке, Шарп пришел к выводу, что вовсе не обязательно определять ковариацию каждой акции друг с другом. Вполне достаточно установить, как каждая акция взаимодействует со всем рынком. И поскольку речь идет о ценных бумагах, то, следовательно, нужно взять в расчет весь объем рынка ценных бумаг. Однако нужно иметь в виду, что количество ценных бумаг и прежде всего акций в любой стране достаточно велико. С ними осуществляется ежедневно громадное количество сделок, как на биржевом, так и внебиржевом рынке. Цены на акции постоянно изменяются, поэтому определить какие-либо показатели по всему объему рынка оказывается практически невозможным. В то же время установлено, что если мы выберем некоторое количество определенных ценных бумаг, то они смогут достаточно точно охарактеризовать движение всего рынка ценных бумаг. В качестве такого рыночного показателя можно использовать фондовые индексы. По теории У. Шарпа, риск портфеля снижается, если число акций в портфеле увеличивается. Средний портфель, составленный из двух случайно выбранных акций, будет иметь стандартное отклонение около 25%. Если число акций довести до 10, то риск снижается примерно до 18%. Портфель, состоящий из всех акций, который принято называть рыночным портфелем, должен был бы иметь стандартное отклонение около 15,1%. Таким образом, половина риска, присущего средней отдельной акции, может быть исключена, если акции будут находиться в портфеле, состоящем из 40 и более акций. Тем не менее, риск всегда остается, как бы широко ни был диверсифицирован портфель. [26, с.79] Деятельность инвесторов всегда связана с риском. Специфический фирменный риск обусловлен такими явлениями, как изменения в законодательстве, забастовки, маркетинговая программа, заключение контрактов и т.п. Рыночный риск, влияющий на все фирмы, может быть обусловлен такими явлениями, как война, инфляция, спад производства, повышение процентных ставок и пр. Поэтому, вкладывая деньги в бумаги, инвесторы в любом случае рискуют. В процессе регулирования портфельных инвестиций могут меняться цели вкладчика, это приводит к изменению портфеля. Обновление портфеля сводится к пересмотру соотношения между доходностью и риском входящих ценных бумаг. В дальнейшем целью регулирования портфельных инвестиций является поддержание тех инвестиционных качеств объекта инвестирования, ради которых был создан портфель ценных бумаг. Портфель подлежит периодической ревизии (пересмотру), с тем чтобы его содержимое не пришло в противоречие с изменившейся экономической обстановкой, инвестиционными качествами отдельных ценных бумаг, а также целями инвестора. Институциональные инвесторы проводят ревизию своих портфелей довольно часто, нередко — ежедневно. 3. ПРОБЛЕМЫ ПОРТФЕЛЬНОГО ИНВЕСТИРОВАНИЯ И ПУТИ РЕШЕНИЯ Прежде всего, следует отметить невозможность ведения нормальных статистических рядов по большинству финансовых инструментов, то есть отсутствие исторической статистической базы, что приводит к невозможности применения в современных российских условиях классических западных методик, да и вообще любых строго количественных методов анализа и прогнозирования. Следующая проблема общего характера - это проблема внутренней организации тех структур, которые занимаются портфельным менеджментом. Как показывает опыт общения с нашими клиентами, особенно региональными, даже во многих достаточно крупных банках до сих пор не решена проблема текущего отслеживания собственного портфеля (не говоря уж об управлении). В таких условиях нельзя говорить о каком-либо более или менее долгосрочном планировании развития банка в целом. Проблемы взаимодействия клиентов и доверительных управляющих. Проблема выбора управляющего в настоящее время решается на уровне личных отношений. Сейчас сложилась практика, когда инвесторы выбирают себе доверительного управляющего не по таким объективным критериям, как финансовая устойчивость, отношение к клиенту, наличие квалифицированного персонала и т. п., а по знакомству, что зачастую приводит к серьезным конфликтам и разочарованиям. Даже если банк или финансовая компания декларируют, что занимаются данным видом деятельности, получить у них исчерпывающую информацию, необходимую для принятия решения об инвестировании, затруднительно. Примерным ориентиром могли бы служить типовые формы договоров и схемы распределения прибыли, однако нормы договорных взаимоотношений на российском рынке пока еще не выработаны, и бытующие формы договоров и оговариваемые ими условия отличаются друг от друга весьма значительно. Названия заключаемых договоров обычно содержат такие понятия как "траст" или "доверительное управление". Тем не менее, часто банки и иные финансовые организации довольствуются брокерскими операциями. Договоры, заключаемые фактически на брокерское обслуживание, содержат в себе инородные блоки о разделении прибыли и т. п. В настоящее время остро стоит проблема прозрачности действий управляющих и их низкой ответственности перед клиентами. Практика показывает, что существует определенная тенденция (особенно среди небанковских доверительных управляющих), когда четкое разделение собственных средств управляющего и средств клиентов не проводится, а ведется синтетический учет одновременно нескольких портфелей, и группировка договоров и платежей осуществляется не по принадлежности операции к портфелю того или иного клиента, а по типу актива. Удивительно, но хотя это в первую очередь отвечает их интересам, клиенты очень редко требуют от управляющих твердых договоренностей относительно отчетности. Ведь если речь идет о трасте в смысле доверительного управления, клиент обязательно должен требовать полной прозрачности действий управляющего. К сожалению, ситуация, когда управляющий, пользуясь непрозрачностью отчетности, трактует статистические данные в свою пользу, очень распространена. Проблемы моделирования и прогнозирования Большой блок проблем связан с процессом математического моделирования и управления портфелями ценных бумаг. Портфель финансовых активов - это сложный финансовый объект, имеющий собственную теоретическую базу. Таким образом, при прогнозировании встают проблемы моделирования и применения математического аппарата, в частности, статистического. Конечно, в ряде случаев, когда можно говорить не о портфеле, а о некоторых элементах " портфельного подхода", удается обойтись более простыми приемами, но перед каждым, кто занимается данной проблематикой, рано или поздно встают серьезные расчетные и исследовательские задачи. Причем универсального подхода к решению всех возникающих задач не существует, и специфика конкретного случая требует модификации базовых моделей. На данный момент адекватного математического аппарата для всех возможных схем еще не разработано. Это связано как с небольшим опытом развития подобных взаимоотношений в России, так и с объективной математической сложностью возникающих моделей. Особенно велико разнообразие моделей в трасте доверительного управления, а именно он наиболее распространен в России. Проблемы оптимального достижения целей инвестирования. Независимо от выбираемого уровня прогнозирования и анализа, для постановки задачи формирования портфеля необходимо четкое описание параметров каждого инструмента финансового рынка в отдельности и всего портфеля в целом (то есть точное определение таких понятий, как доходность и надежность отдельных видов финансовых активов, а также конкретное указание, как на основании этих параметров рассчитывать доходность и надежность всего портфеля). Таким образом, требуется дать определение, доходности и надежности, а также спрогнозировать их динамику на ближайшую перспективу. При этом возможны два подхода: эвристический - основанный на приблизительном прогнозе динамики каждого вида активов и анализе структуры портфеля, и статистический - основанный на построении распределения вероятности доходности каждого инструмента в отдельности и всего портфеля в целом. Второй подход практически решает проблему прогнозирования и формализации понятий риска и доходности, однако степень реалистичности прогноза и вероятность ошибки при составлении вероятностного распределения находятся в сильной зависимости от статистической полноты информации, а также подверженности рынка влиянию изменения макропараметров. После описания формальных параметров портфеля и его составляющих необходимо описать все возможные модели формирования портфеля, определяемые входными параметрами, которые задаются клиентом и консультантом. Используемые модели могут иметь различные модификации в зависимости от постановки задачи клиентом. Клиент может формировать как срочный, так и бессрочный портфель. Портфель может быть пополняемым или отзываемым. Под пополняемостью портфеля понимается возможность в рамках уже действующего договора увеличивать денежное выражение портфеля за счет внешних источников, не являющихся следствием прироста первоначально вложенной денежной массы. Отзываемость портфеля - это возможность в рамках действующего договора изымать часть денежных средств из портфеля. Пополняемость и отзываемость могут быть регулярными и нерегулярными. Пополняемость портфеля регулярна, если имеется утвержденный сторонами график поступления дополнительных средств. Модификации моделей могут определяться и задаваемыми клиентом ограничениями на риски. Уместно вводить также ограничение на ликвидность портфеля (оно вводится на случай возникновения у клиента непредусмотренной в договоре необходимости срочного расформирования всего портфеля). Уровень ликвидности определяется как число дней, необходимое для полной конвертации всех активов портфеля в денежные средства и перевода их на счет клиента. Следующий блок проблем связан уже непосредственно с решением оптимизационных задач. Необходимо определиться с главным критерием оптимизации в процедуре формирования портфеля. Как правило, в качестве целевых функций (критериев) могут выступать лишь доходность и риск (или несколько видов рисков), а все остальные параметры используются в виде ограничений. При формировании портфеля возможны три основные формулировки задачи оптимизации: · целевая функция - доходность (остальное - в ограничениях); · целевая функция - надежность (остальное - в ограничениях); · двухмерная оптимизация по параметрам "надежность-доходность" с последующим исследованием оптимального множества решений. Зачастую бывает, что небольшим уменьшением значения одного критерия можно пожертвовать ради значительного увеличения значения другого (при одномерной оптимизации такого рода возможности отсутствуют). Естественно, что многомерная оптимизация требует применения более сложного математического аппарата, но проблема выбора математических методов решения оптимизационных задач - это тема особого разговора. Проблема постановки задачи управления портфелем Следующий уровень в модифицировании базовых моделей возникает при переходе от статических задач (формирование портфеля) к динамическим (управление портфелем). Разумно полагать, что в течение заранее оговоренного промежутка времени (срока действия договора) клиент не может изменить инвестиционные приоритеты. Однако возможность уточнения прогноза по ходу реализации задачи вносит в нее определенный динамизм. Кроме того, срок окончательных расчетов может быть однозначно не определен, и тогда с позиций статистического подхода мы имеем дело со случайным процессом. ЗАКЛЮЧЕНИЕ Основываясь на информации, изложенной в работе, можно сформулировать следующие выводы: Инвестиционный портфель представляет собой определенный набор из корпоративных акций, облигаций с различной степенью обеспечения и риска, а также бумаг с фиксированным доходом, гарантированным государством, т. е. с минимальным риском потерь по основной сумме и текущих поступлений. |
