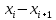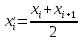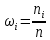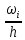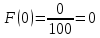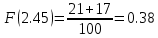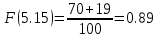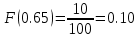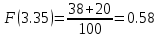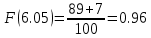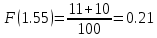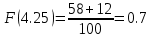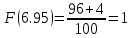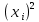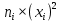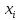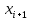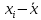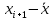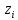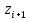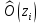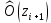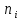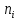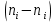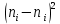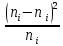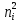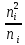7 матан. Иркутский государственный университет путей сообщения
 Скачать 92.38 Kb. Скачать 92.38 Kb.
|
|
Федеральное государственное бюджетное образовательное учреждение высшего образования «Иркутский государственный университет путей сообщения» (ФГБОУ ВО ИрГУПС) Забайкальский институт железнодорожного транспорта - филиал федерального государственного бюджетного образовательного учреждения высшего образования «Иркутский государственный университет путей сообщения» (ЗабИЖТ ИрГУПС) Факультет «Наземные транспортные системы» Кафедра «Прикладная механика и математика»
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА по дисциплине «Математика» РГР.5110140.23.05.05.122-2020.ПЗ
Чита 2020 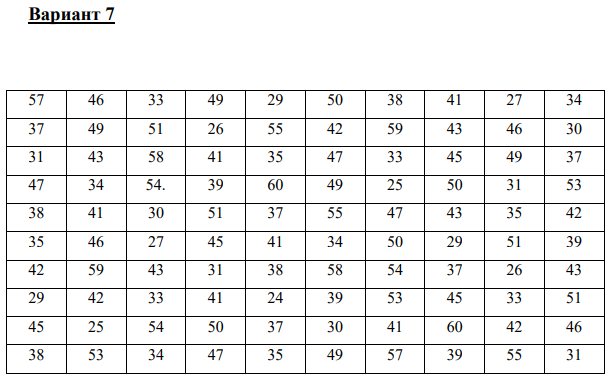 Записываем вариационный ряд (располагаем значение результатов эксперимента в порядке возрастания):
Размах варьирования: 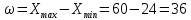 Формула Стёрджесса: 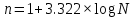 (n-число групп; N-объём выборки) Объём выборки: 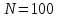 , ,Следовательно: 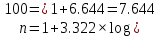 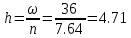 Количество интервалов: 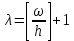 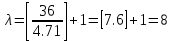
Строим полигон частот: 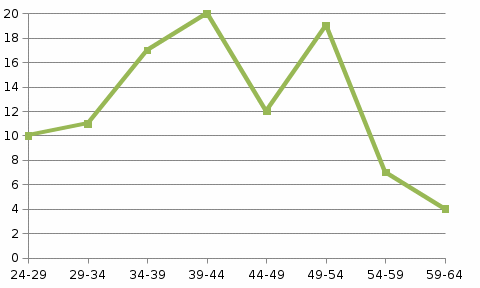 Строим гистограмму относительных частот: 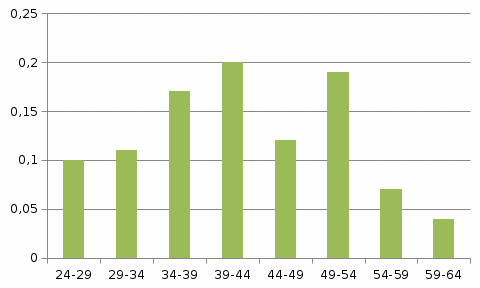 Найдем значения эмпирической функции распределения (функции распределения выборки) – функции, определяющей для каждого значения x относительную частоту события X < x. 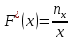
График функции распределения: 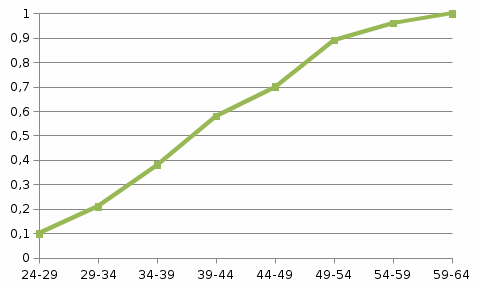 Находим числовые характеристики выборки: Выборочное среднее: 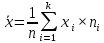 Выборочная дисперсия: 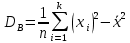 Расчётная таблица:
Получаем: 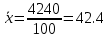 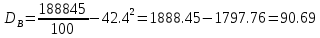 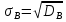 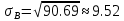 Несмещённой называют статистическую оценку Смещённой называют оценку, математическое ожидание которой не равно оцениваемому параметру. Выборочная дисперсия является смещенной оценкой генеральной дисперсии, а исправленная дисперсия - несмещенной оценкой: 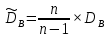 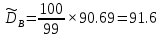 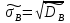 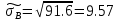 Согласно критерию Пирсона необходимо сравнить эмпирические и теоретические частоты. Эмпирические частоты даны. Найдём теоретические частоты. Для этого пронумеруем Х, т.е. перейдём к случайной величине 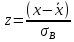 и вычислим концы интервалов: , и вычислим концы интервалов: , 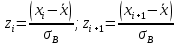 причём наименьшее значение z, точнее z1 положим стремящимся к -∞, а наибольшее, точнее zm+1- стремящемся к +∞ причём наименьшее значение z, точнее z1 положим стремящимся к -∞, а наибольшее, точнее zm+1- стремящемся к +∞( 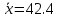 , ,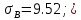 Расчётная таблица:
Находим теоретические вероятности 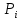 и теоретические частоты: и теоретические частоты: 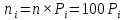 . (Значения и . (Значения и 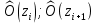 находим по таблице Лапласа.) находим по таблице Лапласа.)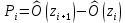 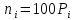 Расчётная таблица:
Вычислим наблюдаемое значение критерия Пирсона: 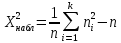 Расчётная таблица:
Контроль: 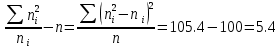 По таблице критических точек распределения 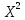 , уровню значимости , уровню значимости 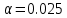 и числу степеней свободы и числу степеней свободы 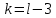 ( (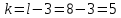 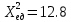 Так как: Так как: 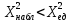 , то гипотеза Н0 о нормальном распределении генеральной совокупности принимается. , то гипотеза Н0 о нормальном распределении генеральной совокупности принимается.Найдем доверительный интервал для математического ожидания для нормального распределения и неизвестной дисперсии. Воспользуемся формулой: 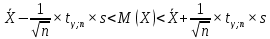 (где 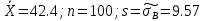 ; ; 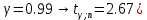 Считаем: 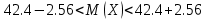 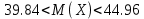 Построим доверительный интервал для среднего квадратического отклонения: 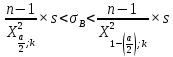 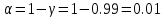 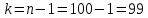 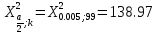 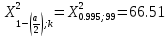 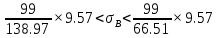 Ответ: Ответ: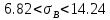 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||