|
|
информатика. Методическая разработка _Иррационал теңдеулерді шешу әдістемесі_. Иррационал тедеулерді шешу Анытама
Иррационал теңдеулерді шешу
Анықтама. 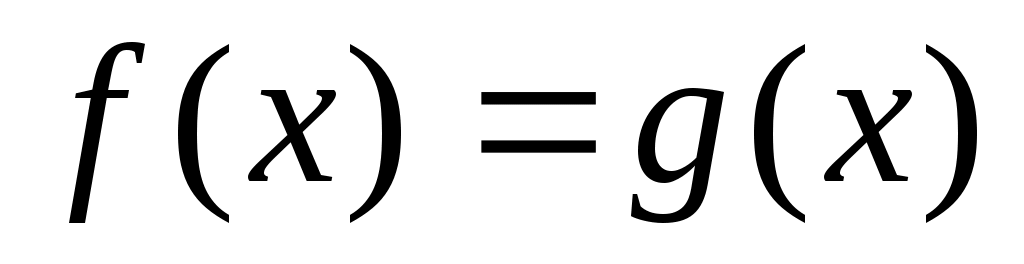 теңдеуі иррационал теңдеу деп аталады, егер f(x) пен g(x) алгебралық өрнектер болса және кем дегенде біреуі иррационал өрнек болса. теңдеуі иррационал теңдеу деп аталады, егер f(x) пен g(x) алгебралық өрнектер болса және кем дегенде біреуі иррационал өрнек болса.
Иррационал теңдеулер нақты сандар жиынында қарастырылады. Мұндай теңдеулерді шешкенде көбінесе табылған түбірлерді теңдеудегі орнына қойып тексеру қажет. Ал, теңдеудің мүмкін мәндер облысы табылған жағдайда тексеру жүргізу қажет емес.
Иррационал теңдеулерді шешудің негізгі әдістерінің бірі – теңдеудің екі бөлігін де бірдей дәрежеге шығару болып табылады. n-жұп болған жағдайда, 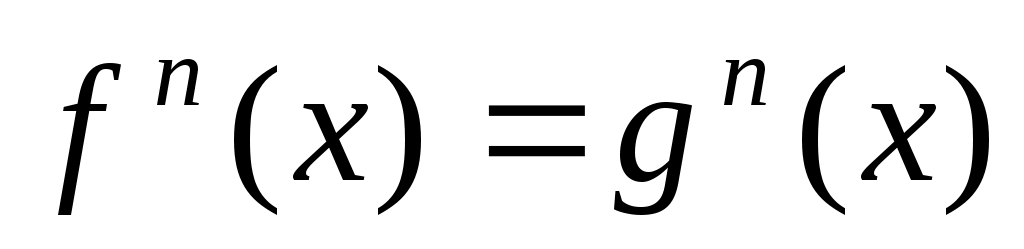 теңдеуі теңдеуі 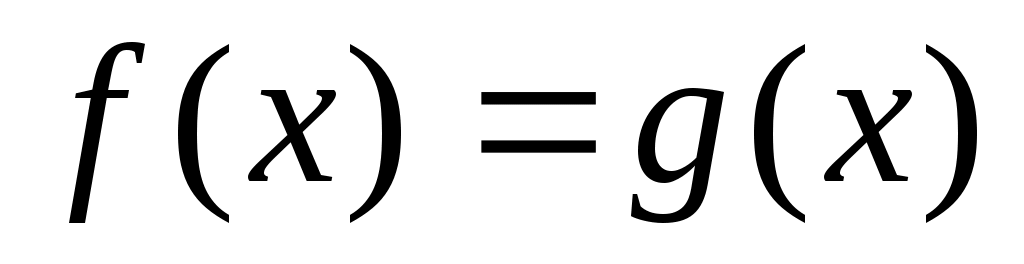 теңдеуінің салдары болады. Ал, n-тақ болған жағдайда бұл екі теңдеу мәндес болады. Демек, теңдеудің екі бөлігін де жұп дәрежеге шығарғанда бөгде түбір пайда болуы ықтимал. Сондықтан мұндай түрлендіру жасалған жағдайда табылған түбірлерді тексеру қажет. теңдеуінің салдары болады. Ал, n-тақ болған жағдайда бұл екі теңдеу мәндес болады. Демек, теңдеудің екі бөлігін де жұп дәрежеге шығарғанда бөгде түбір пайда болуы ықтимал. Сондықтан мұндай түрлендіру жасалған жағдайда табылған түбірлерді тексеру қажет. 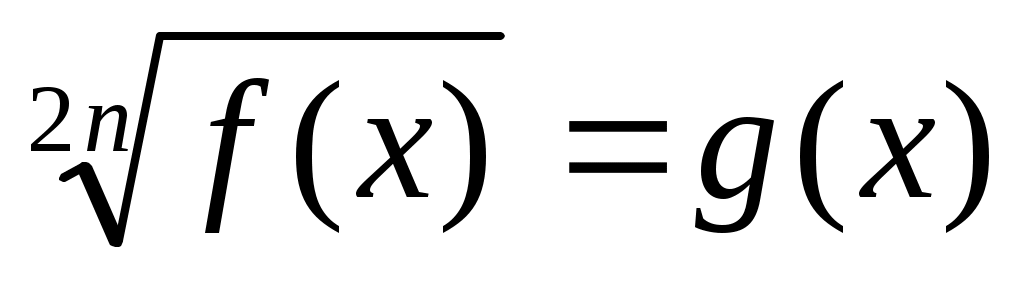 теңдеуі теңдеуі 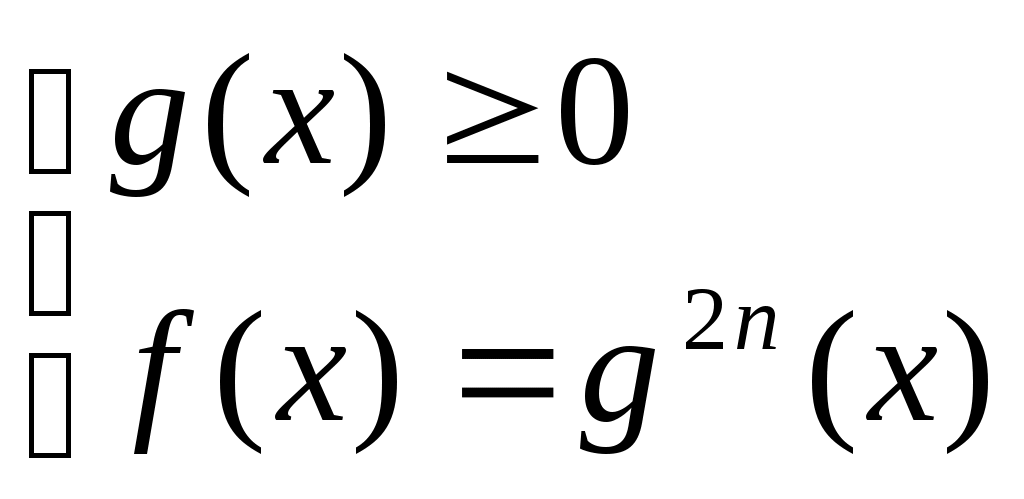 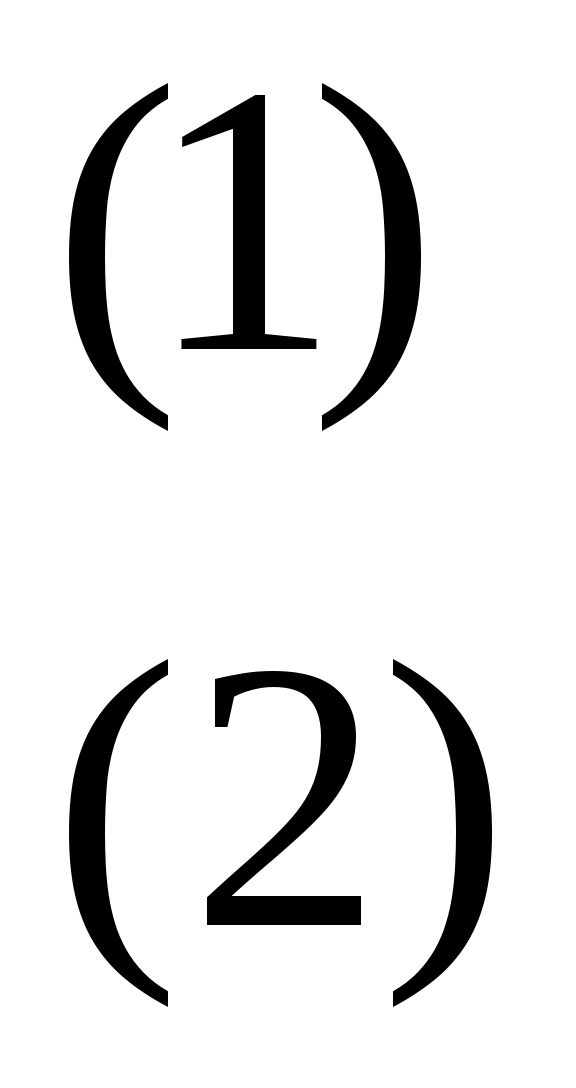 жүйесімен мәндес. Бұл жүйеге жүйесімен мәндес. Бұл жүйеге 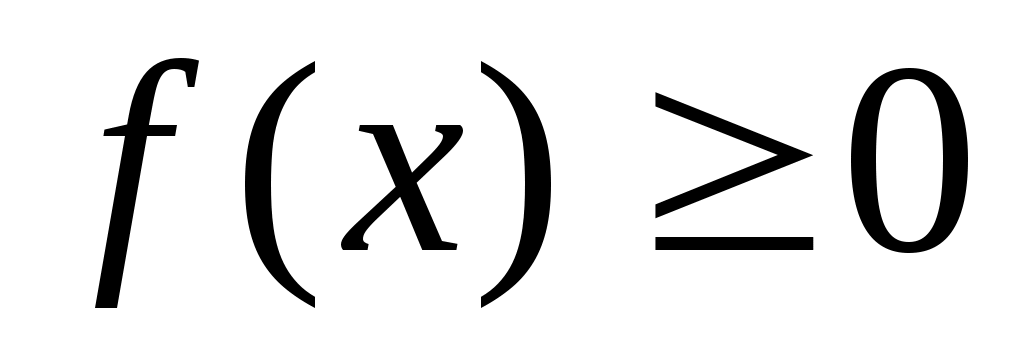 теңсіздігін жазу артық. Өйткені ол (2) теңдеуінің салдары. теңсіздігін жазу артық. Өйткені ол (2) теңдеуінің салдары.
Енді нақты мысалдардан иррационал теңдеулерді шешудің әртүрлі әдістерін қарастырайық.
1-әдіс. Теңдеудің екі бөлігін бірдей дәрежеге шығару.
Мысал 1. 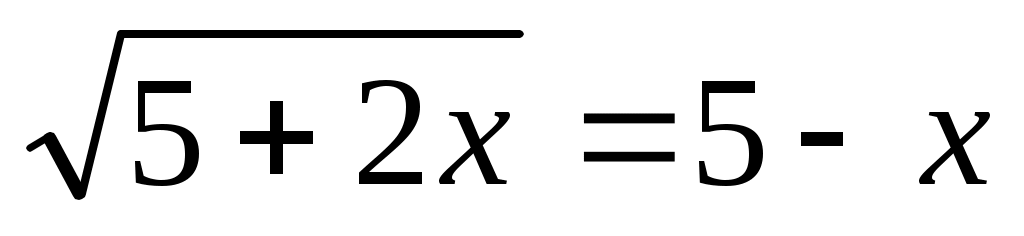 (1) (1)
Шешуі:Берілген теңдеу төмендегі жүйемен мәндес болады.
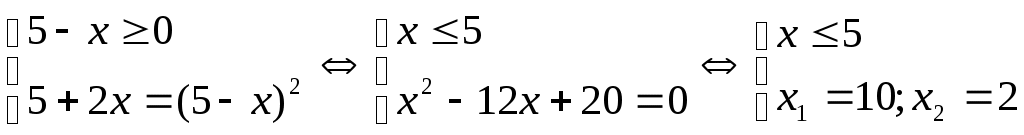
Бұдан 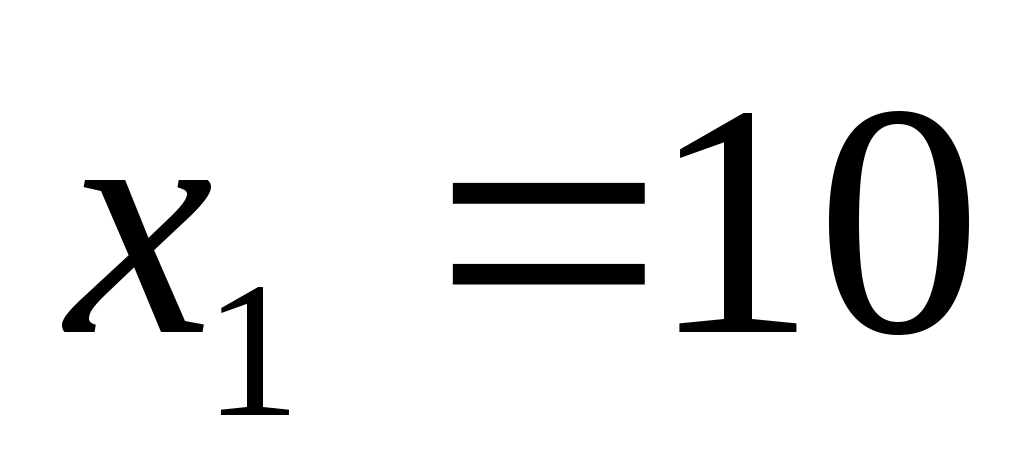 түбірі жүйедегі бірінші теңсіздікті қанағаттандырмайтынын көреміз. Демек, (1) теңдеудің шешімі түбірі жүйедегі бірінші теңсіздікті қанағаттандырмайтынын көреміз. Демек, (1) теңдеудің шешімі 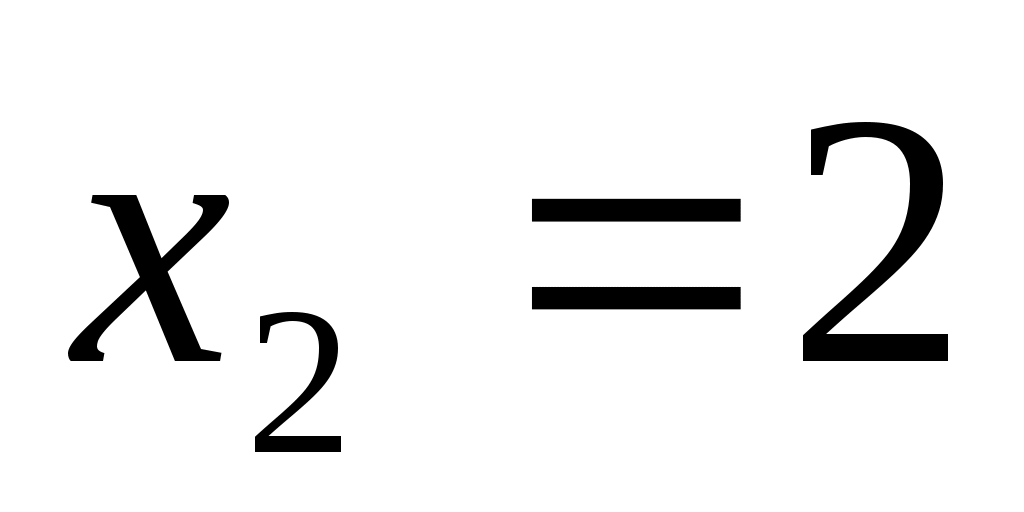 болады. болады.
Жауабы: 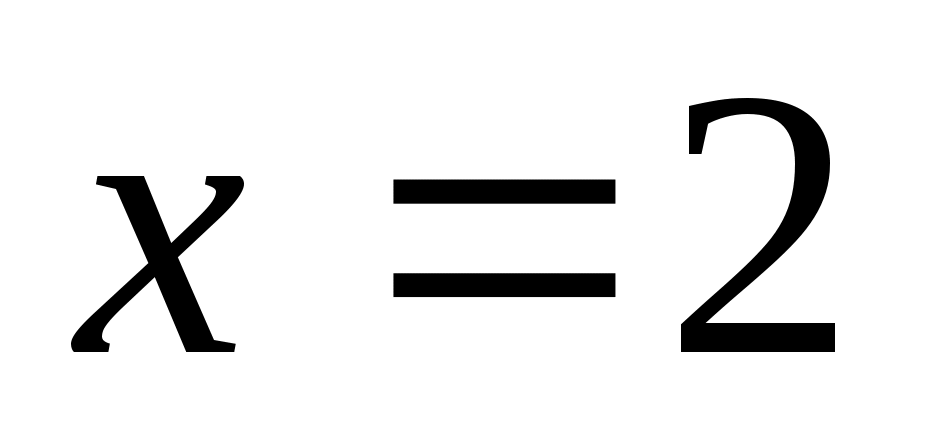
2-әдіс. Функцияның монотондық қасиетін пайдалану.
Анықталу облысы х≥ -2,5. Теңдеудің сол жағы монотонды өспелі, ал оң жағы монотонды кемімелі деп қарастыруға болады. Мұндай жағдайда олардың мәндері бір нүктеде ғана тең болуы мүмкін. Яғни бір ғана шешімі болуы мүмкін. Ол х=2
Мысал 2. 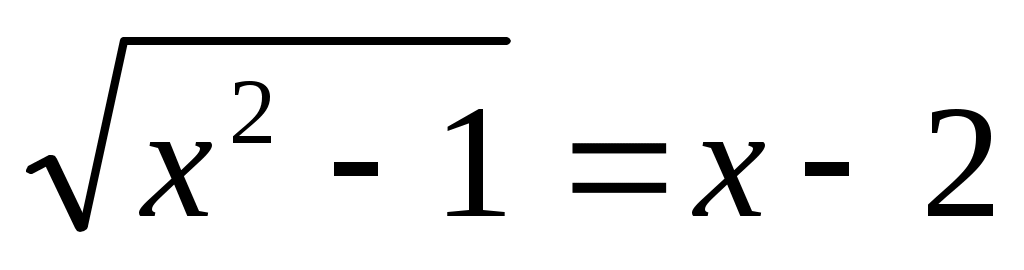 (1) (1)
Шешуі:Берілген теңдеу төмендегі жүйемен мәндес болады.
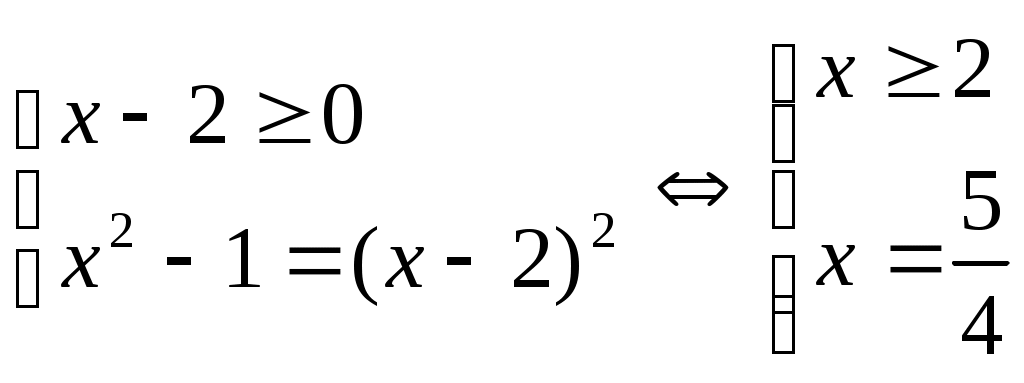 . Бұл жүйенің шешімі жоқ. Өйткені . Бұл жүйенің шешімі жоқ. Өйткені 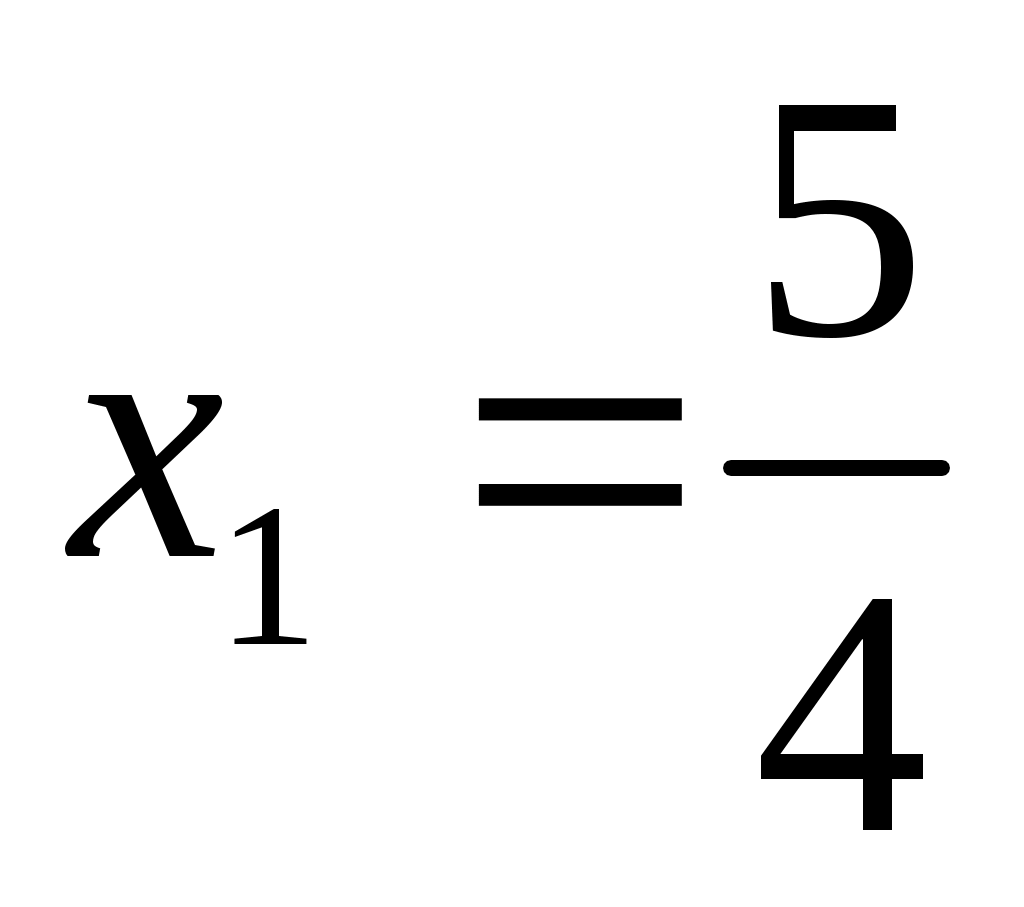 түбірі жүйенің бірінші шартына сәйкес келмейді. түбірі жүйенің бірінші шартына сәйкес келмейді.
Жауабы: шешімі жоқ
Мысал 3. 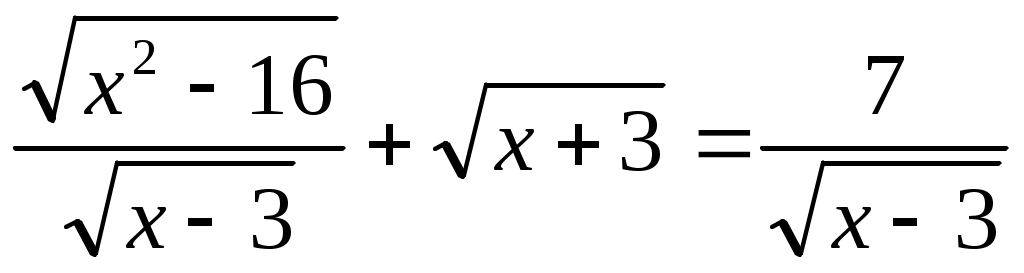 (1) (1)
Шешуі:ММО табайық. Ол үшін төмендегі теңсіздіктер жүйесін шешу керек.
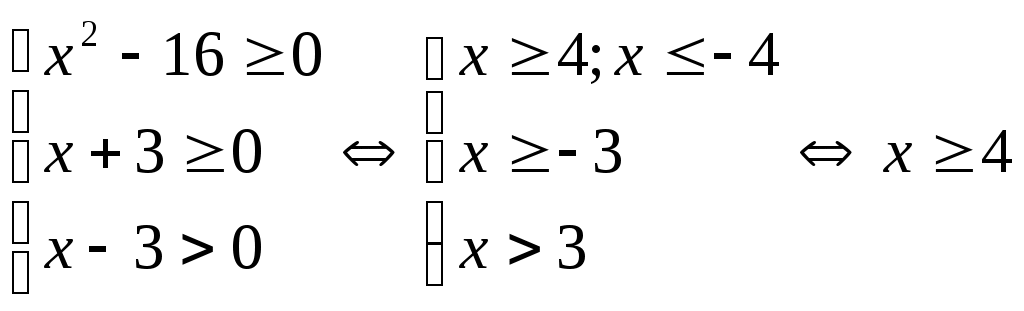 . Сонда ММО: . Сонда ММО: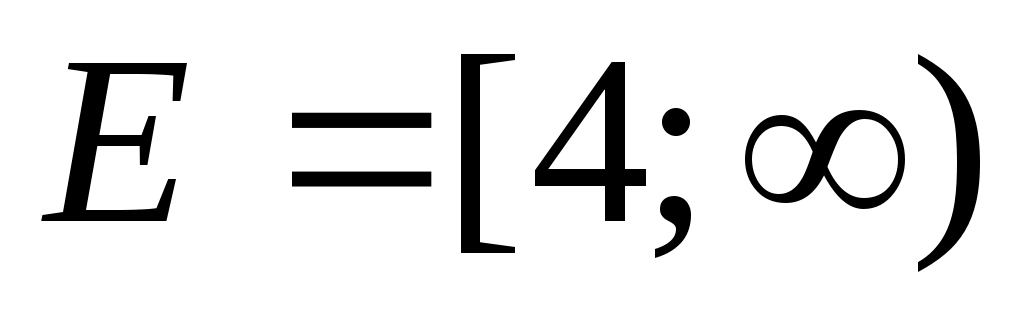 . .
Енді (1) теңдеудің екі бөлігін де 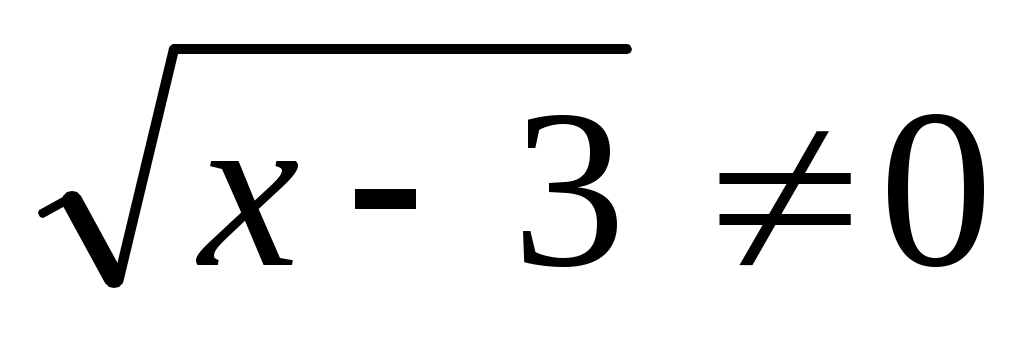 өрнегіне көбейтеміз. Сонда ММО-да (1)-ге мәндес өрнегіне көбейтеміз. Сонда ММО-да (1)-ге мәндес 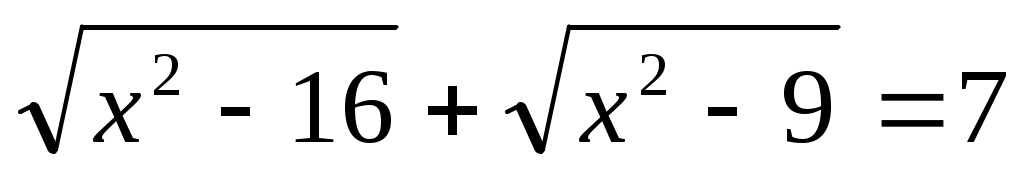 (2) теңдеуі шығады. Бұдан (2) теңдеуі шығады. Бұдан 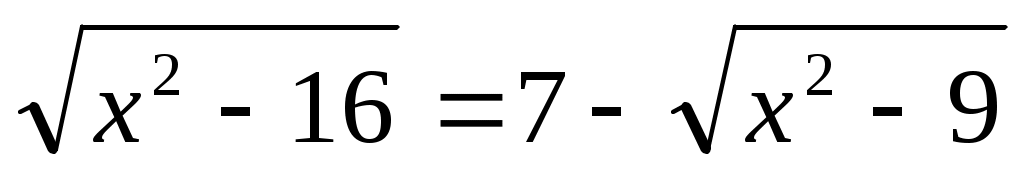 теңдеуін аламыз. Екі жағын квадраттап, ықшамдай отырып, теңдеуін аламыз. Екі жағын квадраттап, ықшамдай отырып, 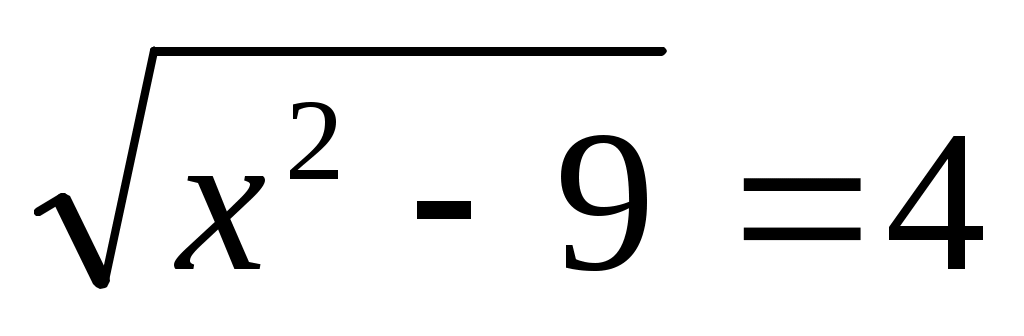 аламыз. аламыз. 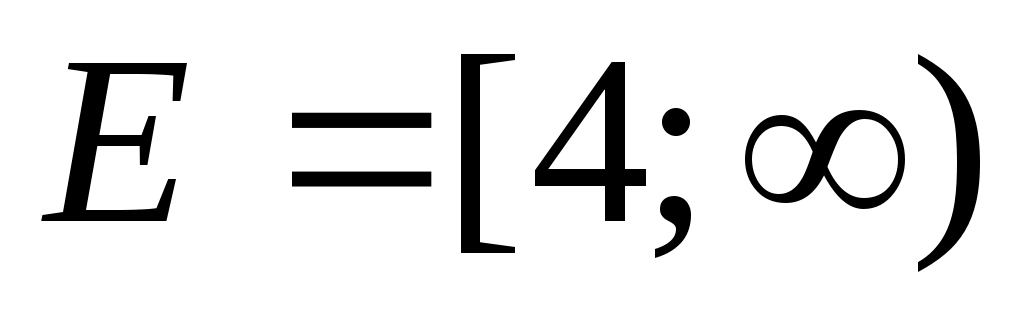 жиынында жиынында 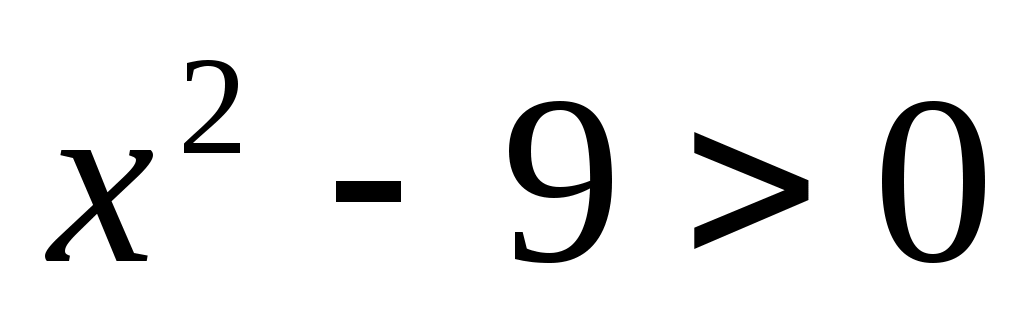 болғандықтан, теңдеудің екі бөлігін квадраттаймыз, болғандықтан, теңдеудің екі бөлігін квадраттаймыз, 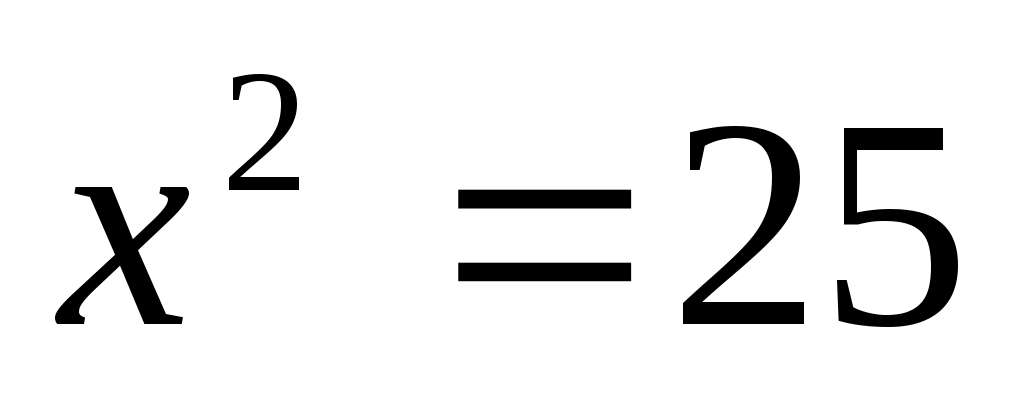 , бұдан , бұдан 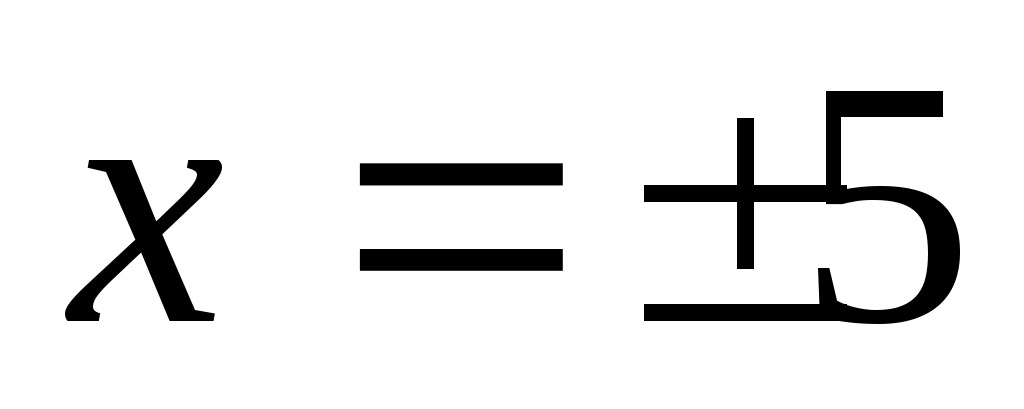 . . 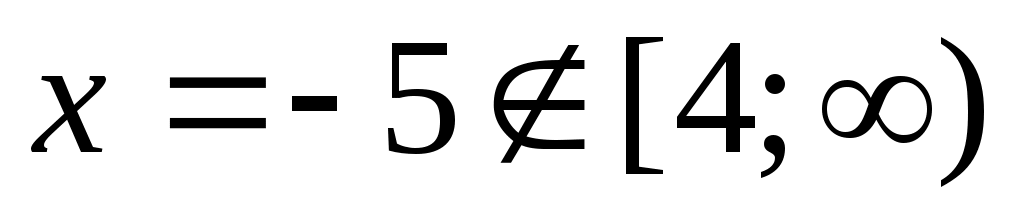 болғандықтан, түбірге алынбайды, яғни болғандықтан, түбірге алынбайды, яғни 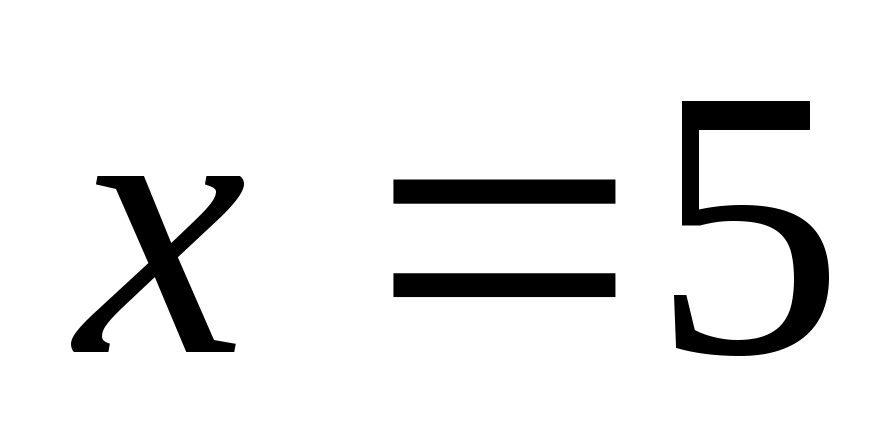 . .
Жауабы: 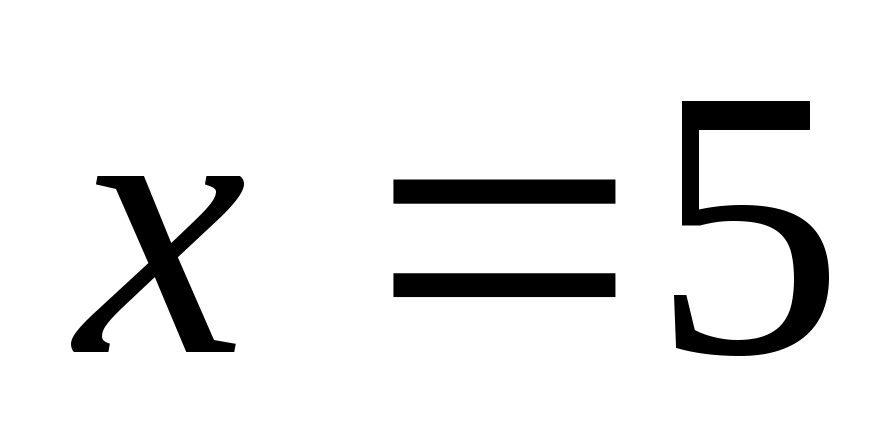
2-әдіс. Функцияның монотондық қасиетін пайдалану.
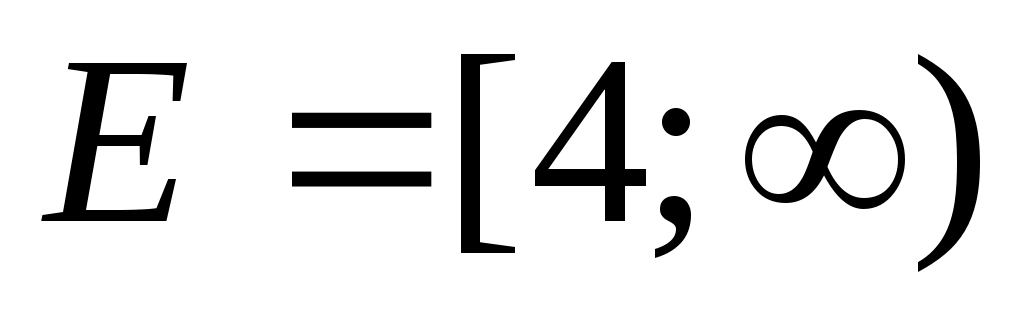 жиынында жиынында 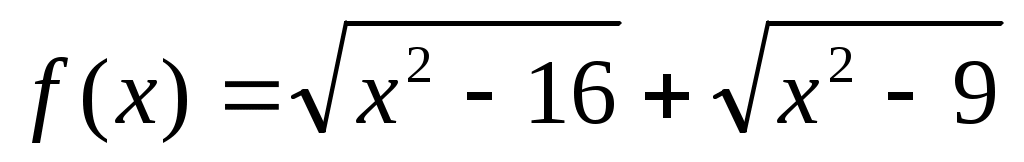 функциясы монотонды өспелі. функциясы монотонды өспелі.
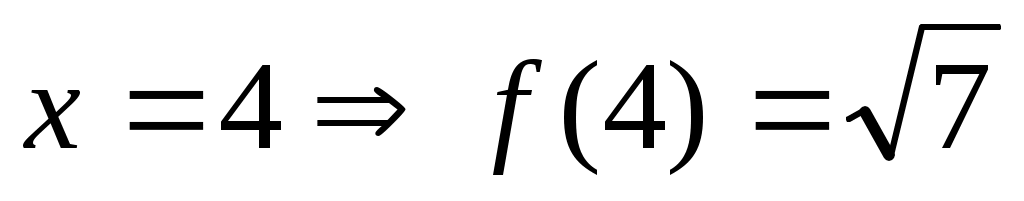 . Сонда . Сонда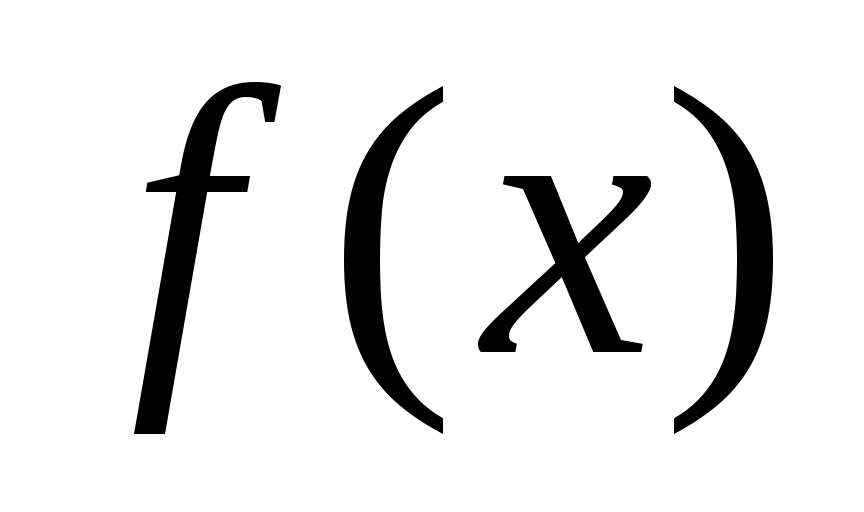 -тің өзгеру облысы -тің өзгеру облысы 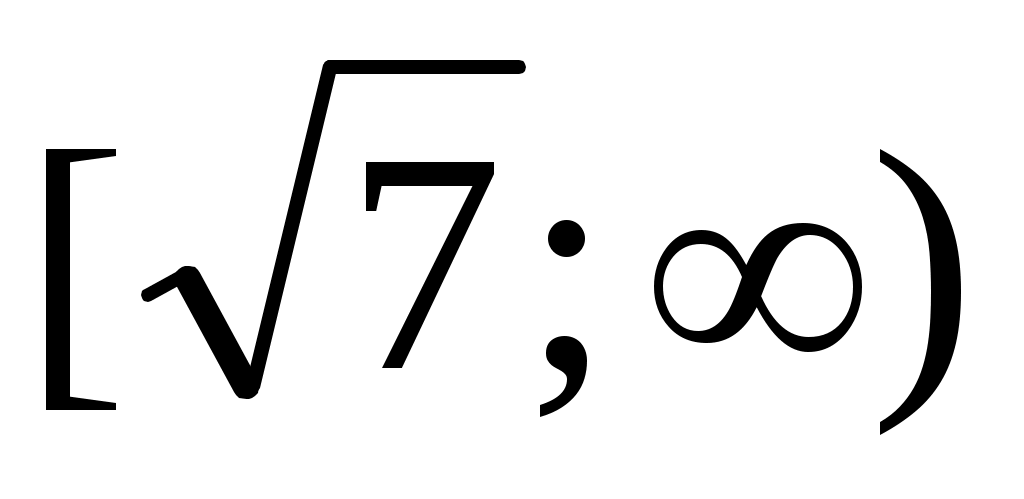 . Демек, теңдеудің тек бір ғана шешім болады. Ол . Демек, теңдеудің тек бір ғана шешім болады. Ол 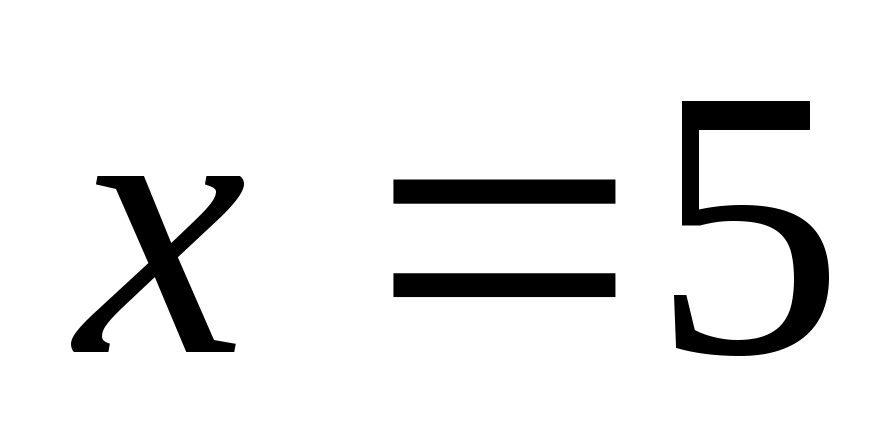 , өйткені , өйткені 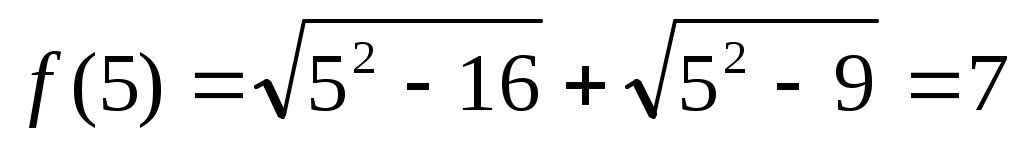
Мысал 4. 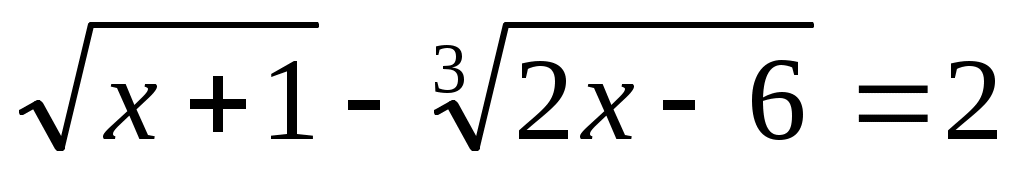 (1) (1)
Шешуі:ММО табамыз. 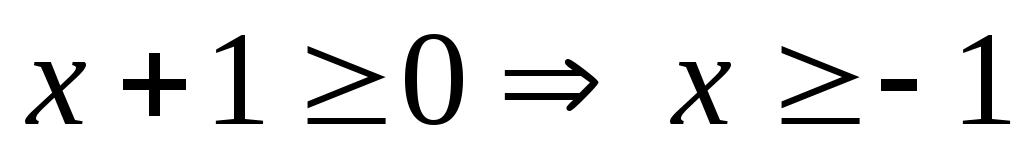 . Демек, . Демек, 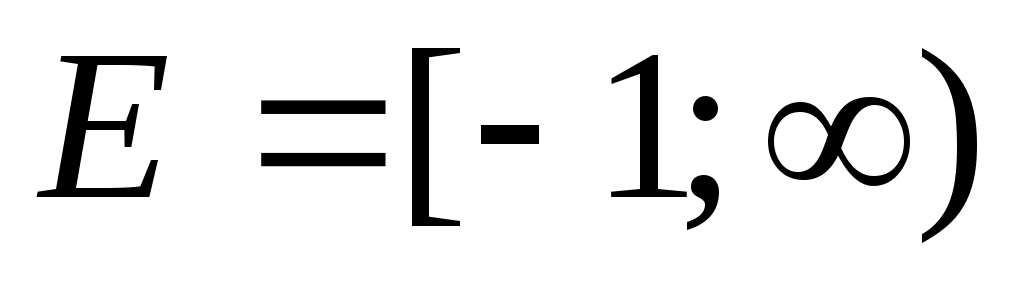 . Түрлендіру ықшам болу үшін . Түрлендіру ықшам болу үшін 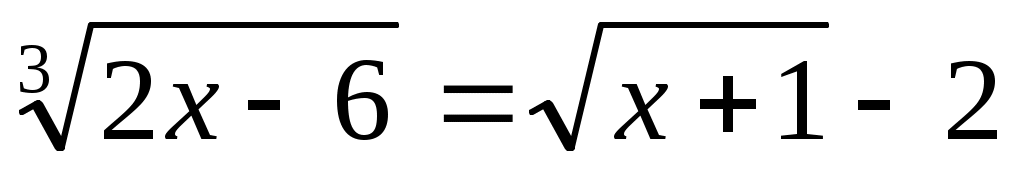 түріне келтіріп, теңдеудің екі бөлігін кубтаймыз. Сонда (1)-ге мәндес түріне келтіріп, теңдеудің екі бөлігін кубтаймыз. Сонда (1)-ге мәндес 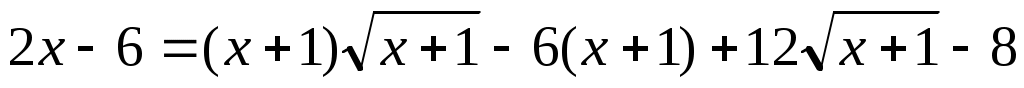 теңдеуін аламыз. Бұдан теңдеуін аламыз. Бұдан 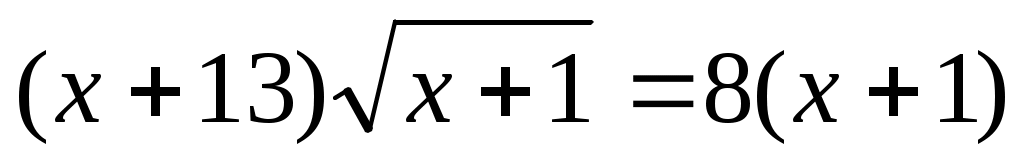 шығады. ММО: шығады. ММО: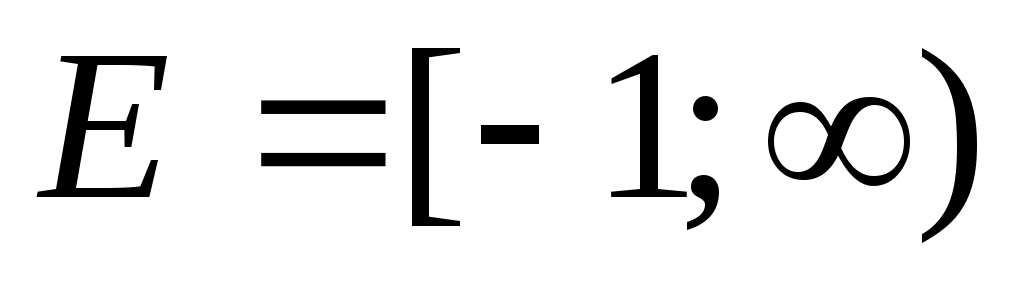 жиынында теңдеудің екі бөлігі де теріс емес болғандықтан, квадраттаймыз. Сонда жиынында теңдеудің екі бөлігі де теріс емес болғандықтан, квадраттаймыз. Сонда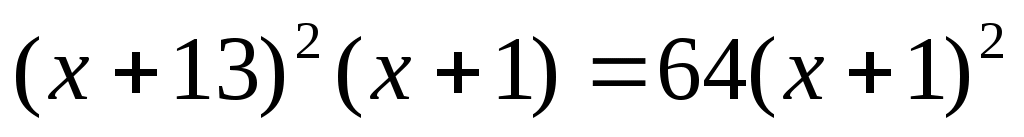 . Бұдан . Бұдан 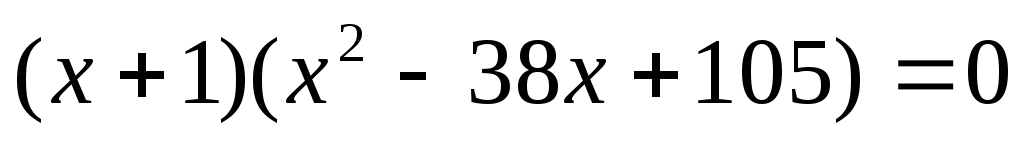 . Яғни . Яғни 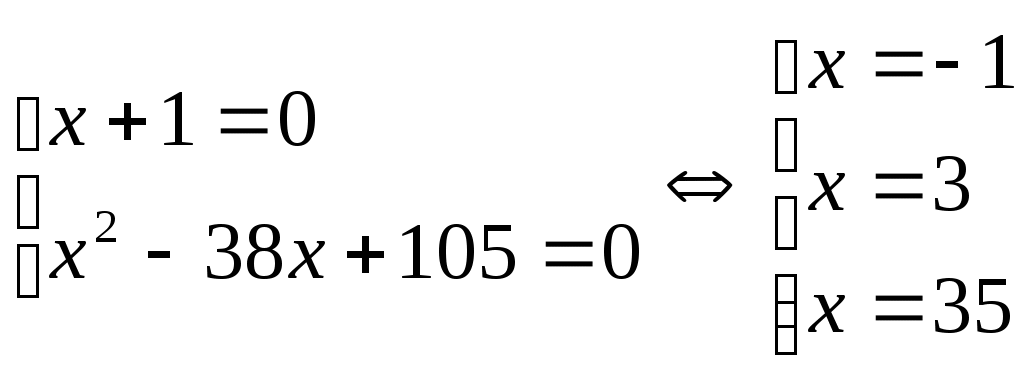 . Бұл табылған түбірлер МОО-на тиісті . Бұл табылған түбірлер МОО-на тиісті 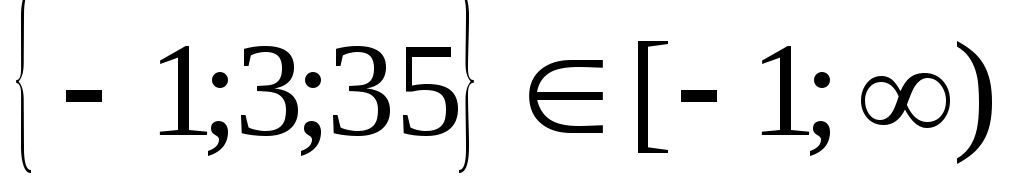
Жауабы: 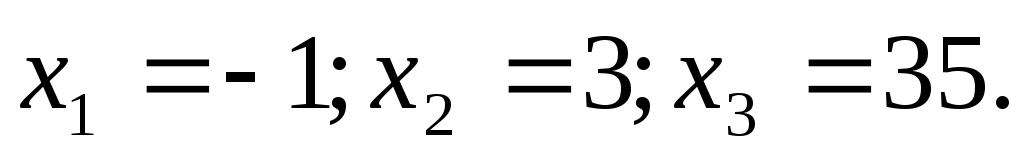
Мысал 5. 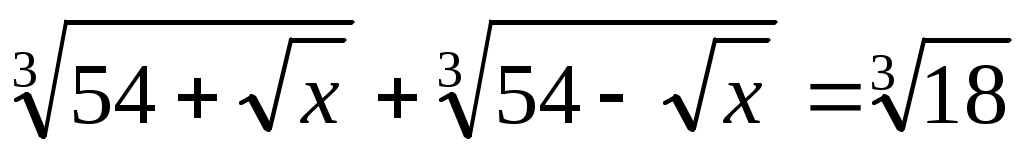 (1) (1)
Шешуі:ММО табамыз. 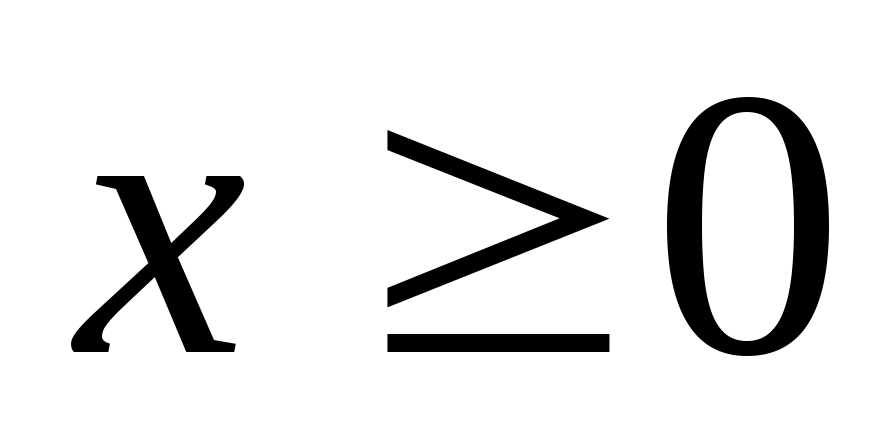 . Демек, . Демек, 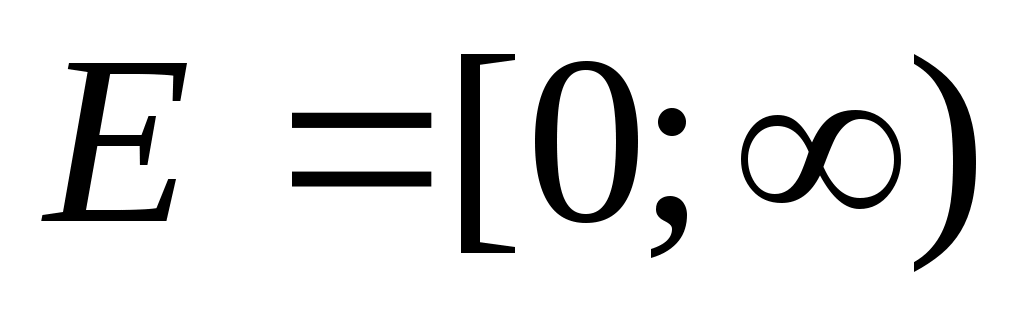 . Енді . Енді 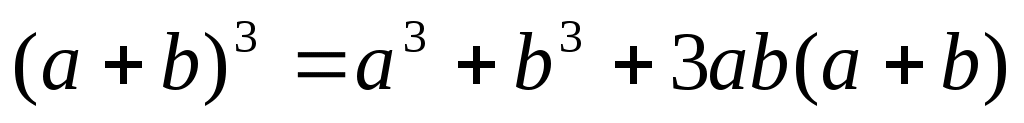 формуласын пайдаланып, теңдеудің екі бөлігін кубтаймыз. Сонда (1)-ге ММО-да мәндес теңдеу аламыз. формуласын пайдаланып, теңдеудің екі бөлігін кубтаймыз. Сонда (1)-ге ММО-да мәндес теңдеу аламыз.
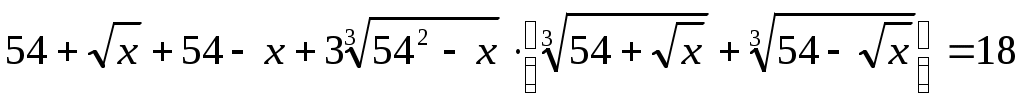 . Тік жақша ішіндегі өрнекті (1) теңдеудегі . Тік жақша ішіндегі өрнекті (1) теңдеудегі 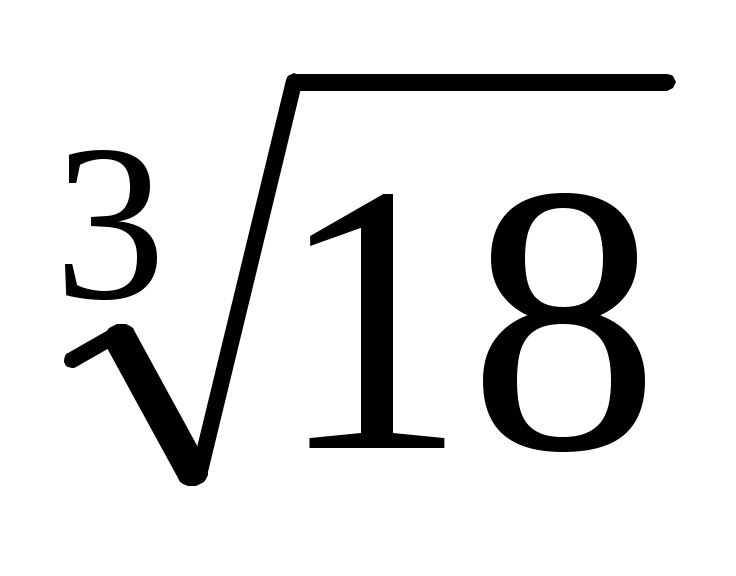 санымен алмастырамыз. Сонда санымен алмастырамыз. Сонда 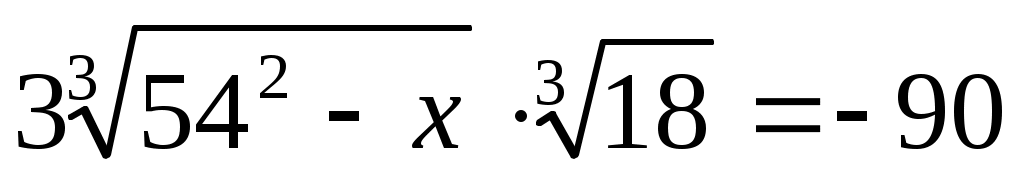 теңдеуін аламыз. Бұдан теңдеуін аламыз. Бұдан 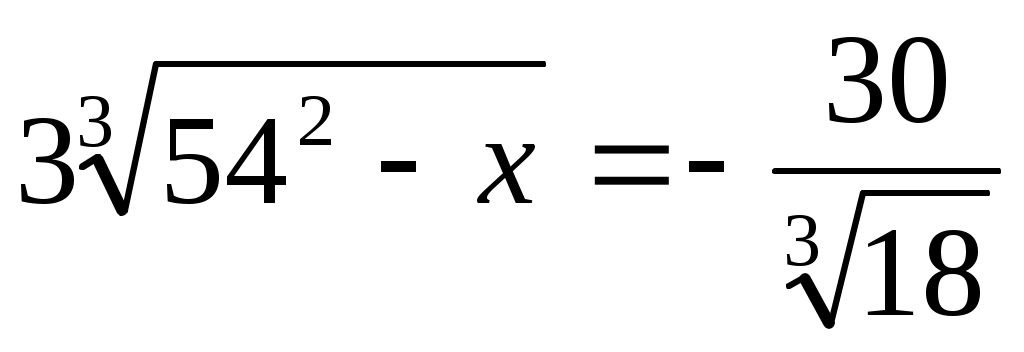 . Теңдеудің екі бөлігін кубтаймыз. Сонда (1) теңдеуге мәндес . Теңдеудің екі бөлігін кубтаймыз. Сонда (1) теңдеуге мәндес 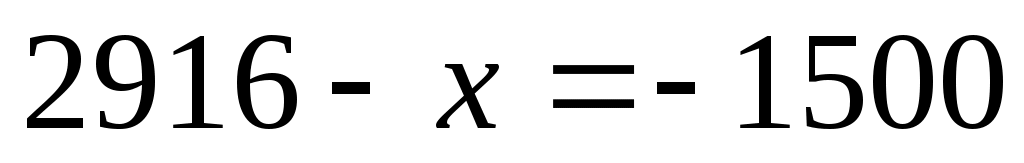 , бұдан , бұдан 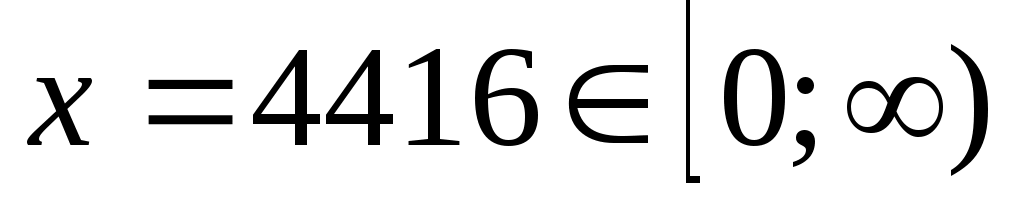 түбірін аламыз. түбірін аламыз.
Жауабы: 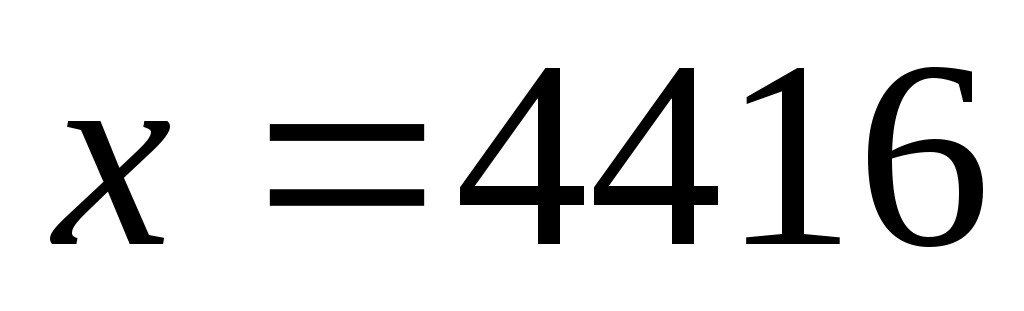
3-әдіс. Қос түбір формуласын қолдану.
Мысал 6. 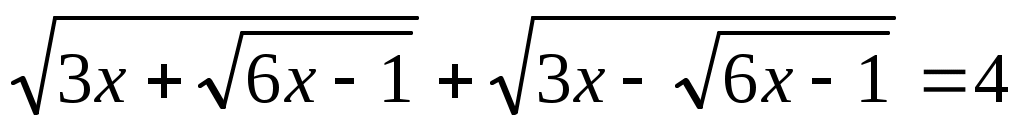 (1) (1)
Шешуі:Бұл теңдеуді шешпес бұрын қос түбір формуласына тоқталайық. Қос түбірден тұратын 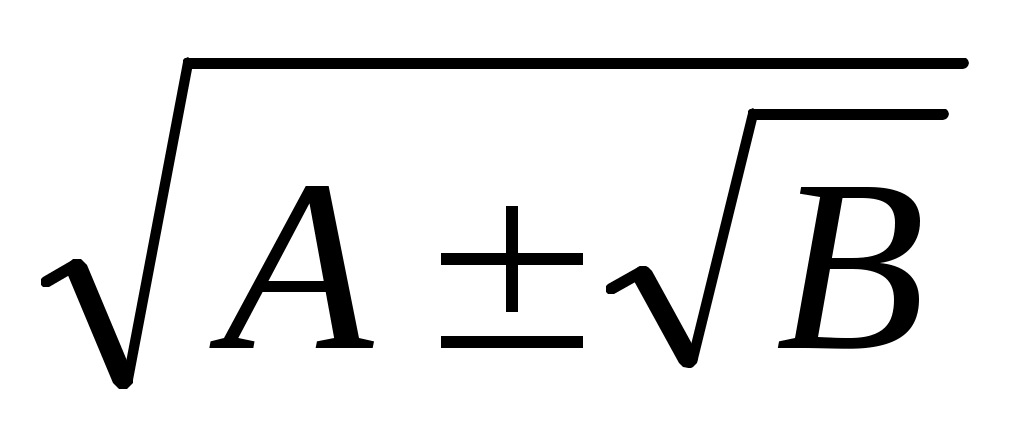 өрнегін түрлендіруде өрнегін түрлендіруде 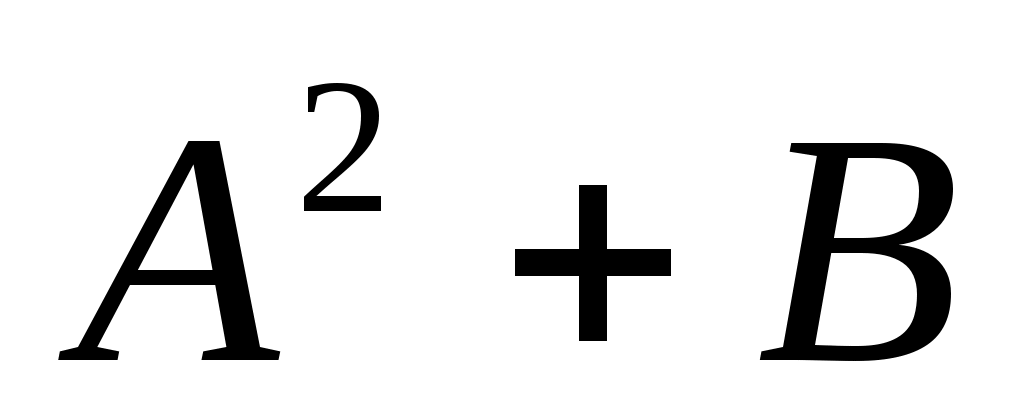 өрнегі толық квадрат болғанда төмендегі формула қолайлы. өрнегі толық квадрат болғанда төмендегі формула қолайлы. 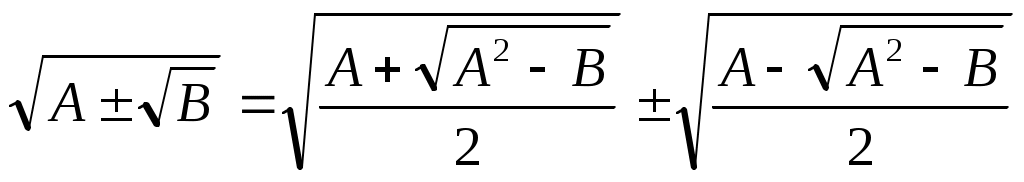 . Осыформуланы берілген теңдеуге қолдансақ, . Осыформуланы берілген теңдеуге қолдансақ, 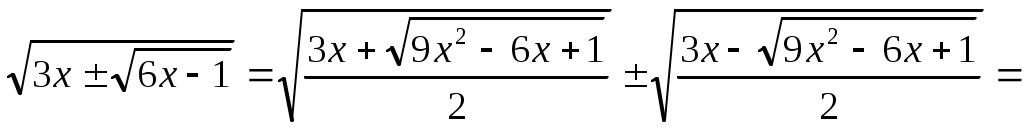 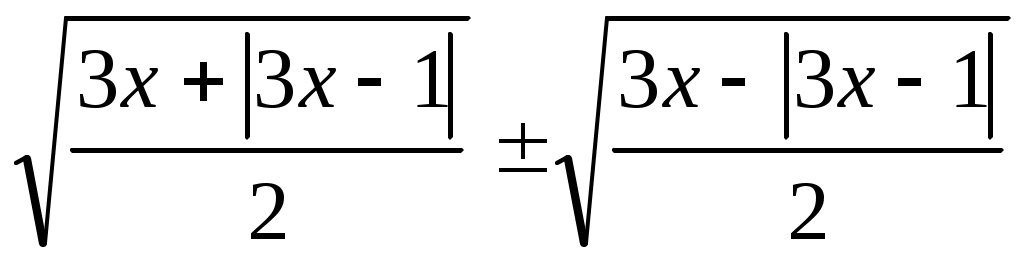 болғандықтан, (1)-дегі орнына қойсақ, болғандықтан, (1)-дегі орнына қойсақ, 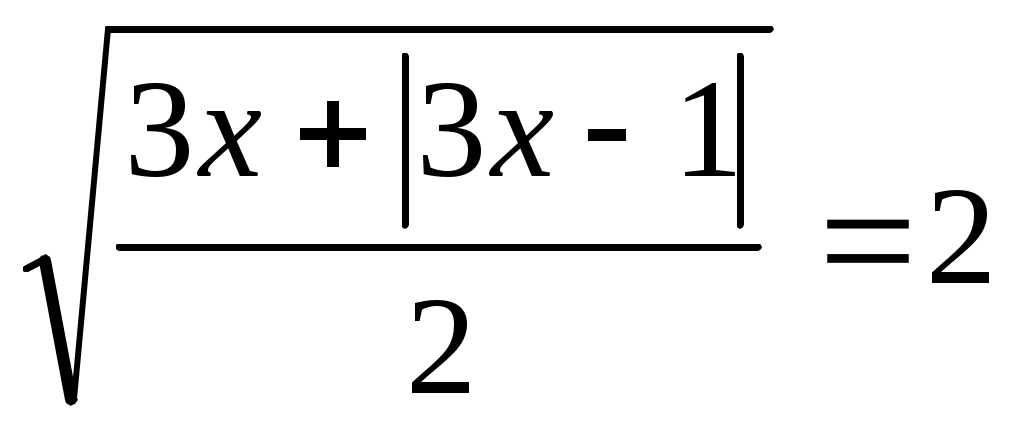 шығады. Теңдеудің екі бөлігін квадраттап, шығады. Теңдеудің екі бөлігін квадраттап, 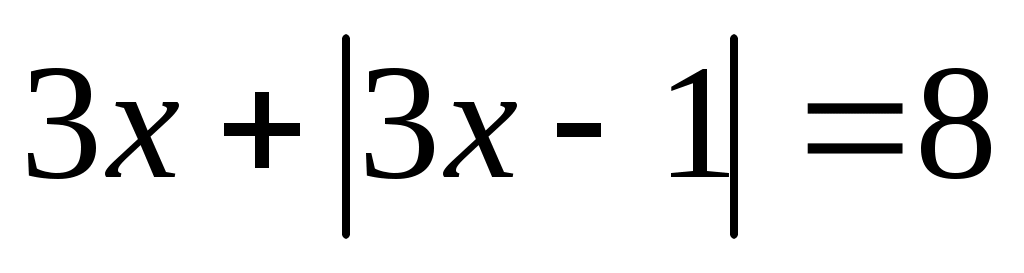 (2) теңдеуін аламыз. Модуль жақшасын ашамыз: (2) теңдеуін аламыз. Модуль жақшасын ашамыз: 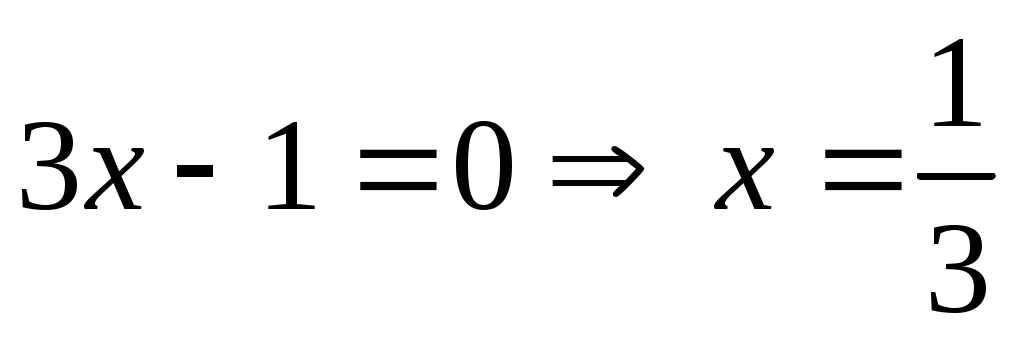
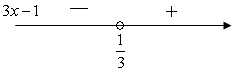
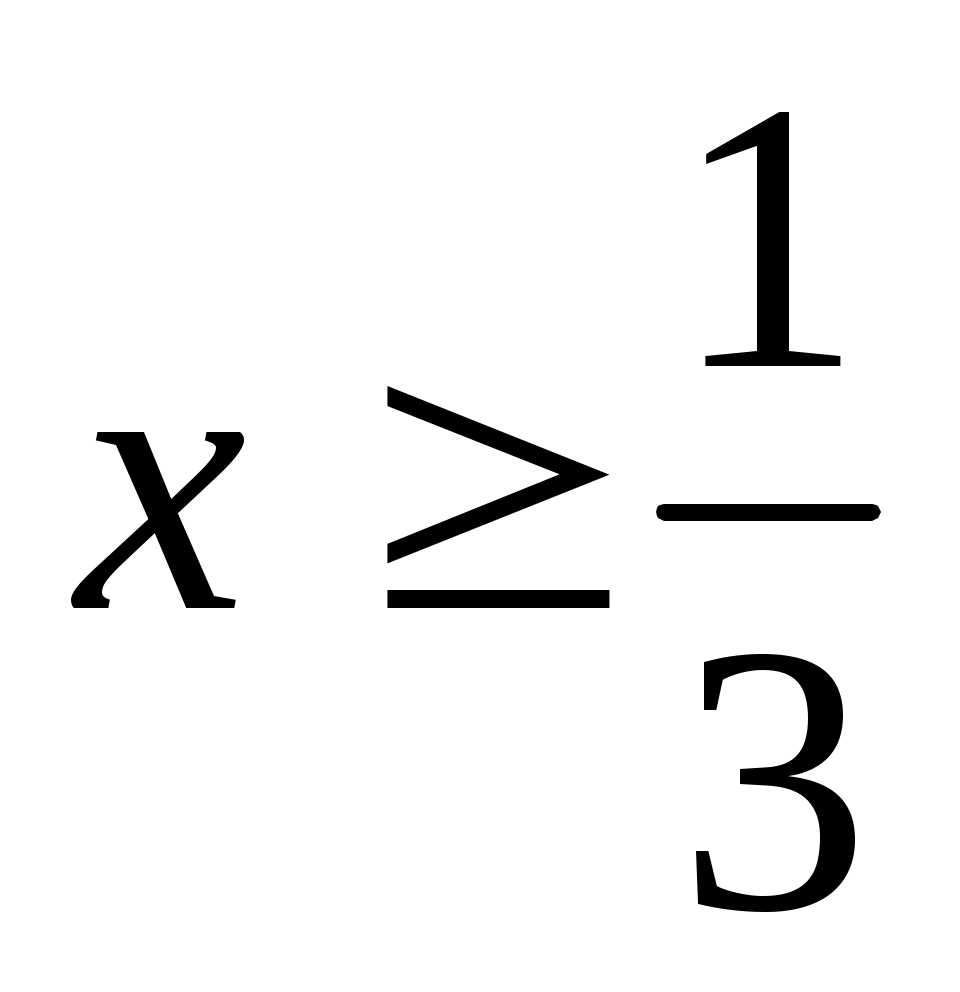 болғанда, болғанда, 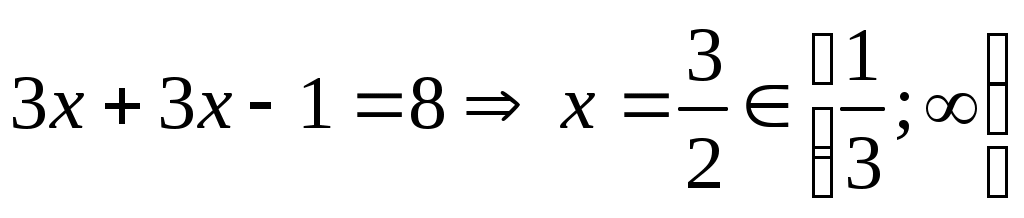 болғандықтан, болғандықтан, 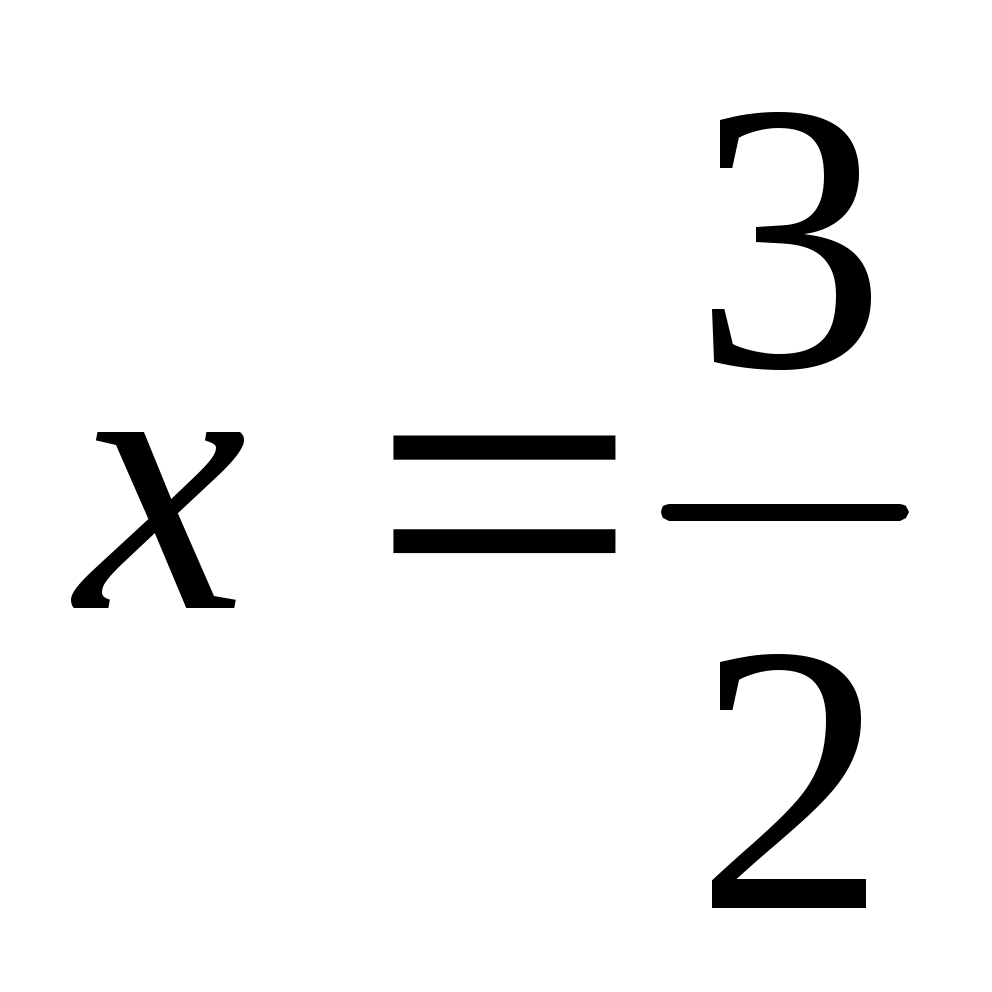 мәні (2) теңдеуіне, сондай-ақ (2)-ге мәндес болатын (1) теңдеуіне шешім болады. мәні (2) теңдеуіне, сондай-ақ (2)-ге мәндес болатын (1) теңдеуіне шешім болады.
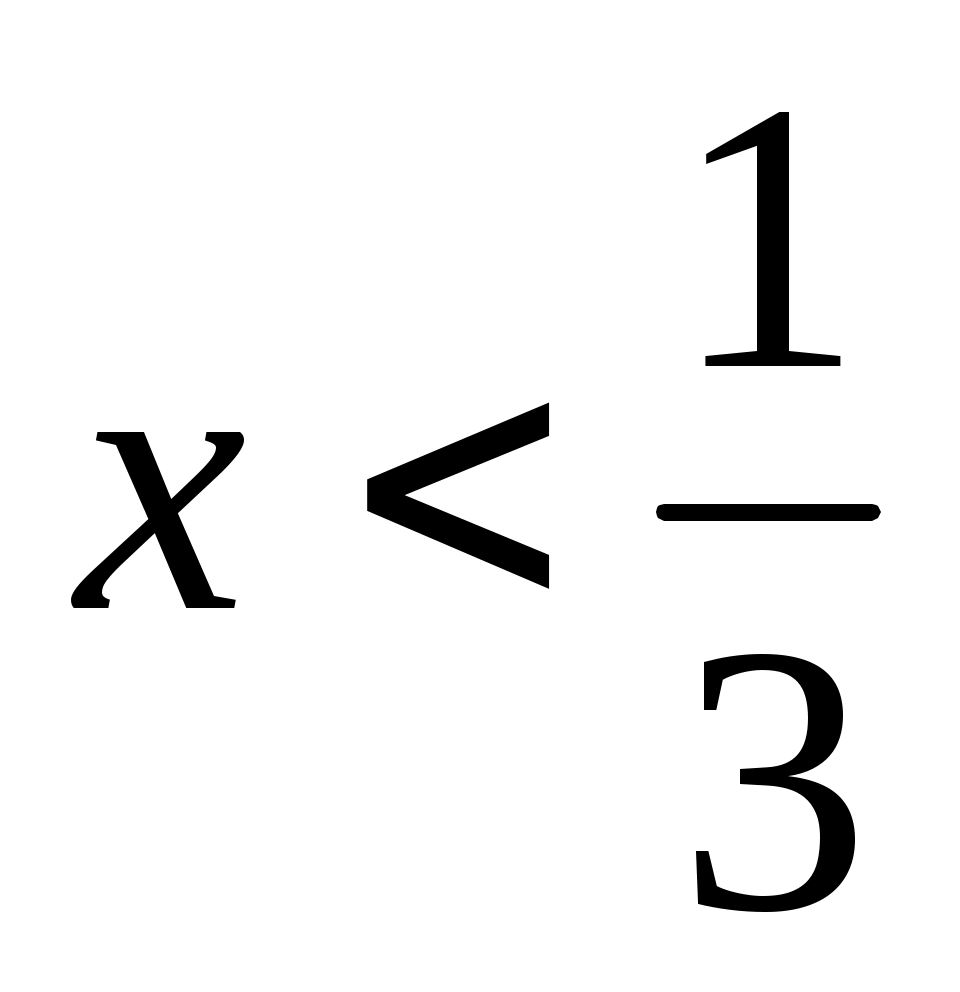 болғанда, болғанда, 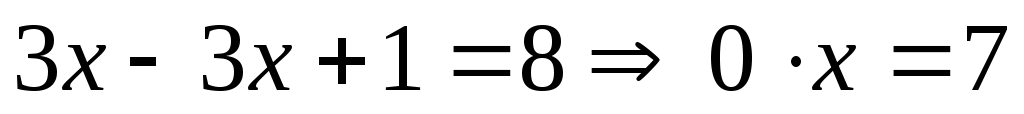 теңдеуінің шешімі жоқ. теңдеуінің шешімі жоқ.
Жауабы: 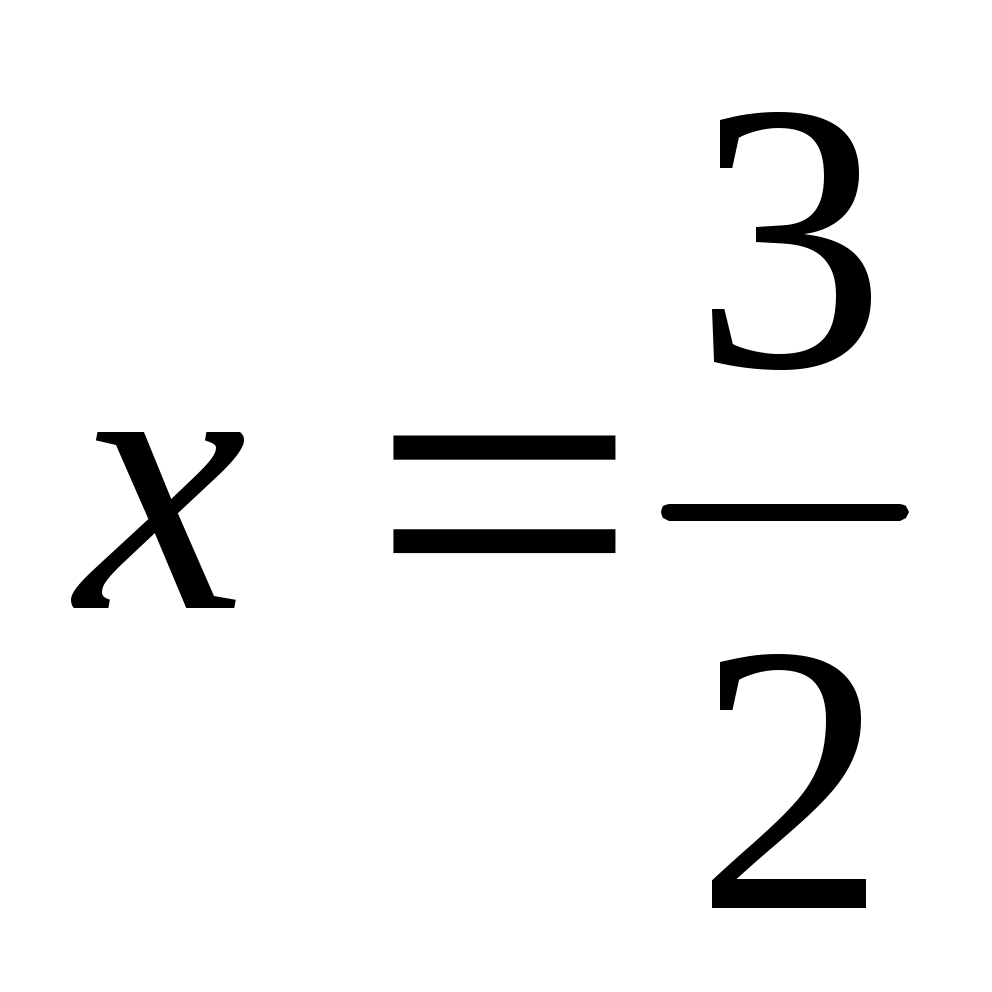
4-әдіс. Түйіндес өрнекке көбейту.
Мысал 7. 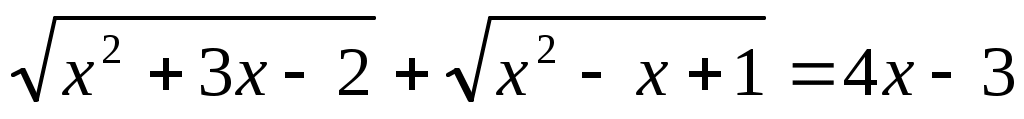 (1) (1)
Шешуі: Теңдеудің екі бөлігін де теңдеудің сол жақ бөлігіндегі өрнекке түйіндес болатын 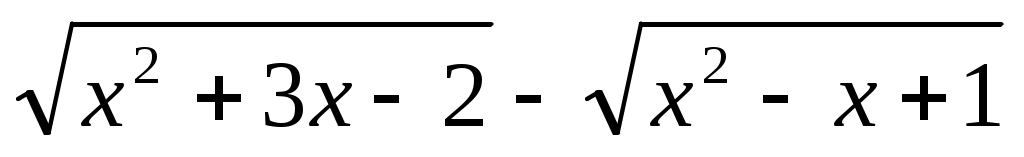 өрнегіне көбейтеміз. өрнегіне көбейтеміз. 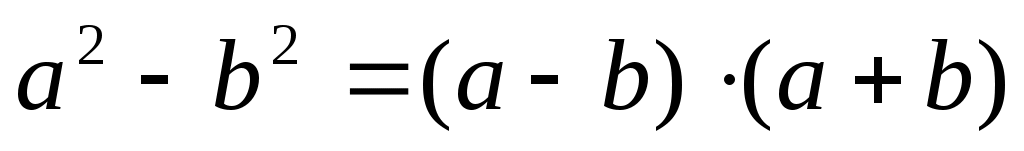 формуласын пайдаланамыз. Сонда ықшамдай отырып, формуласын пайдаланамыз. Сонда ықшамдай отырып,
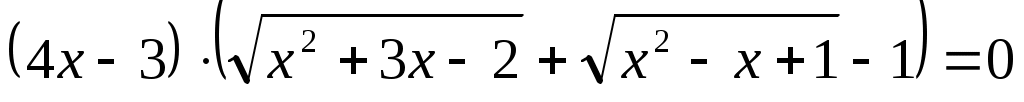 теңдеуін аламыз. теңдеуін аламыз.
Бұдан 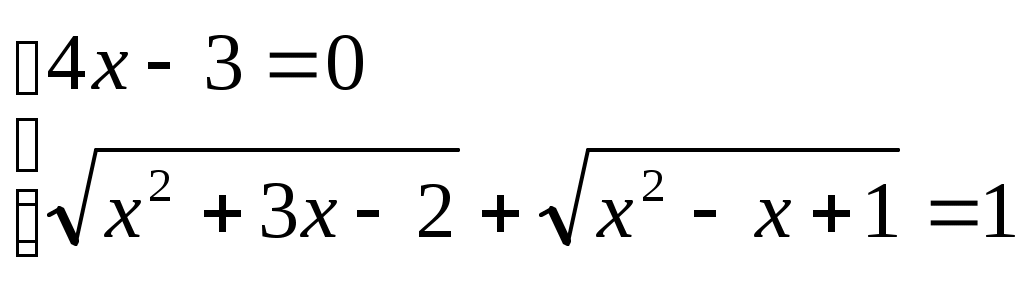 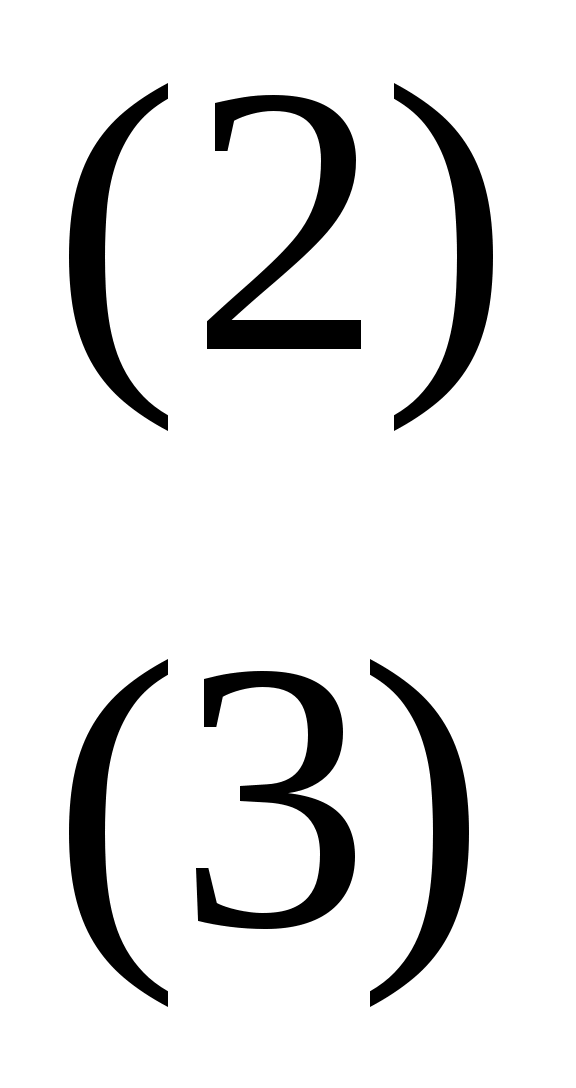 теңдеулер жиынын аламыз. (2)-ден теңдеулер жиынын аламыз. (2)-ден 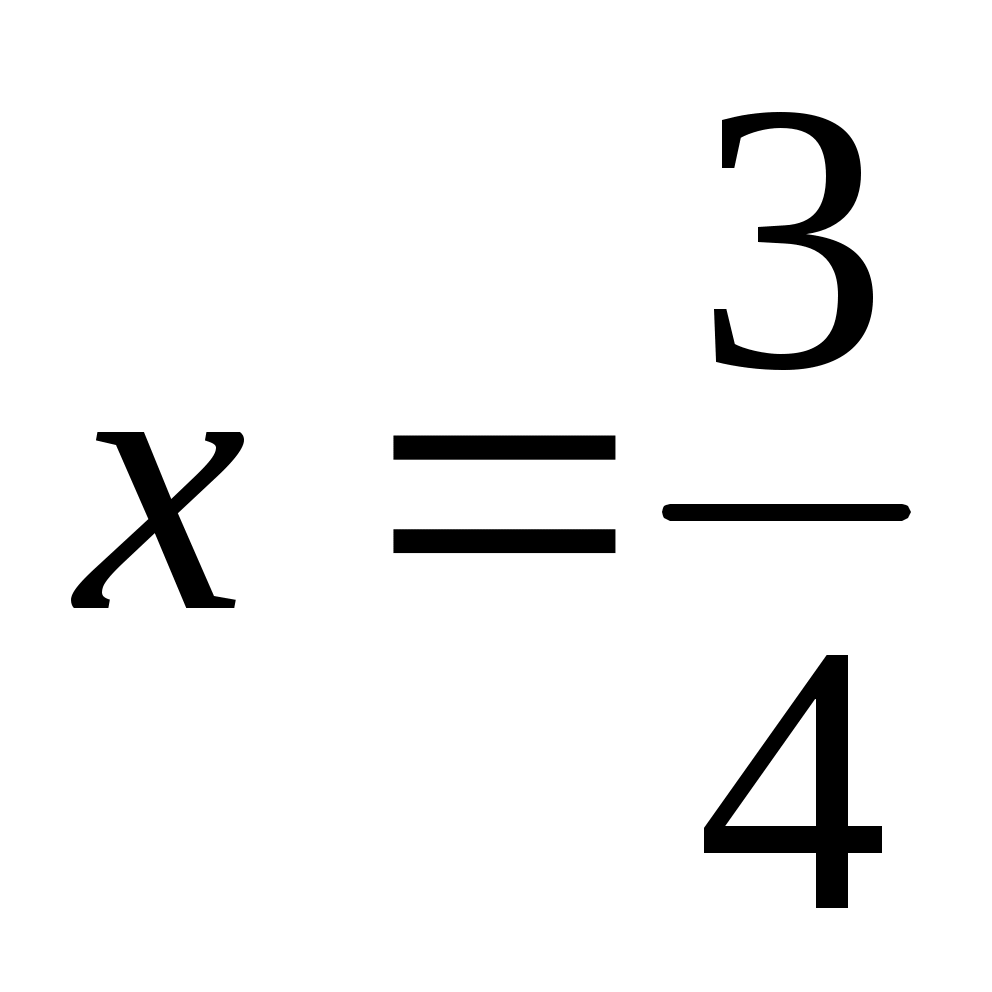 . Біз (3) теңдеуден (1) теңдеудің түбірлерін іздеп отырмыз. Ол түбірлер (1) мен (3) теңдеулердің қосындысы болатын теңдеуге де түбір болады. Яғни (1) мен (3) теңдеулерді мүшелеп қосамыз. Сонда . Біз (3) теңдеуден (1) теңдеудің түбірлерін іздеп отырмыз. Ол түбірлер (1) мен (3) теңдеулердің қосындысы болатын теңдеуге де түбір болады. Яғни (1) мен (3) теңдеулерді мүшелеп қосамыз. Сонда 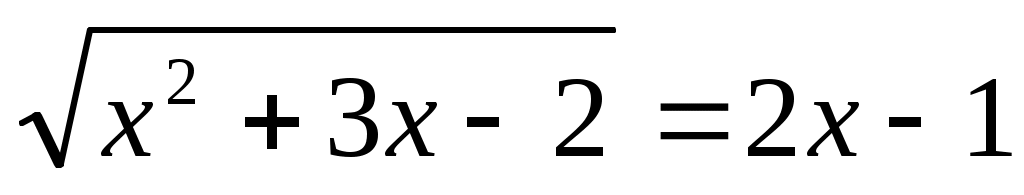 (4) теңдеуі шығады. Ол (1) теңдеудің салдары. Сондықтан соңынан табылған түбірлерді (1) дегі орнына қойып тексеру керек. Енді (4) теңдеуді шешейік. (4) теңдеуі шығады. Ол (1) теңдеудің салдары. Сондықтан соңынан табылған түбірлерді (1) дегі орнына қойып тексеру керек. Енді (4) теңдеуді шешейік.
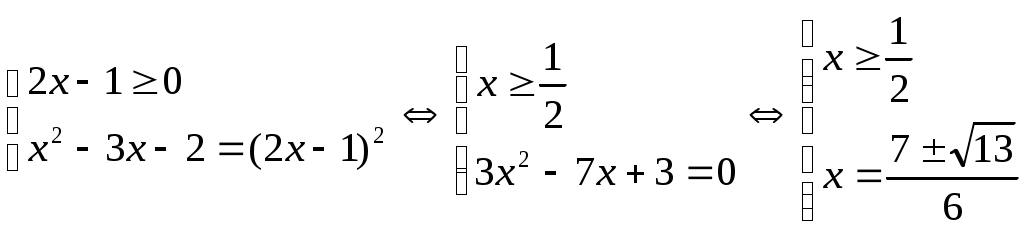 , бұдан , бұдан 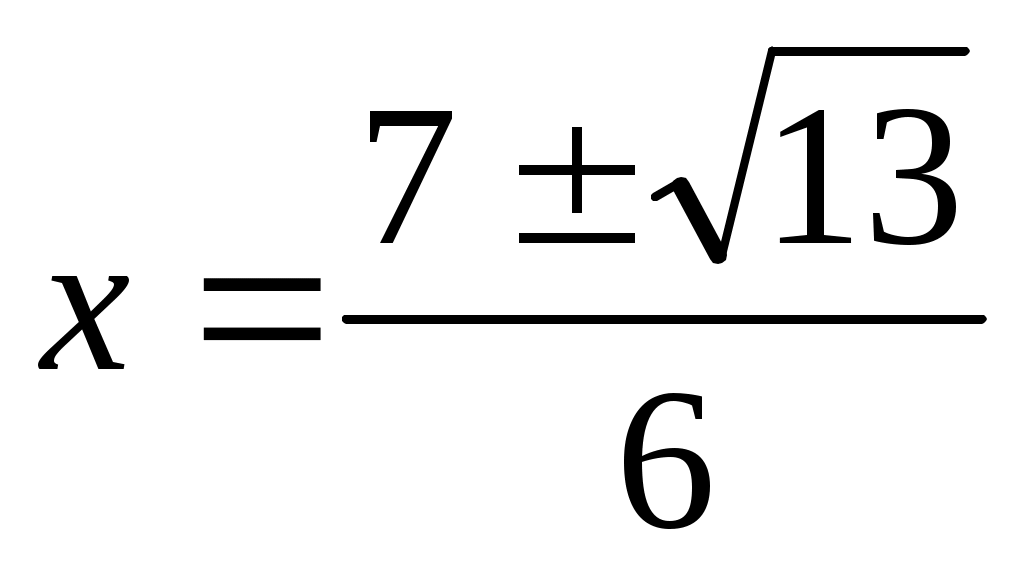 . .
Сонымен 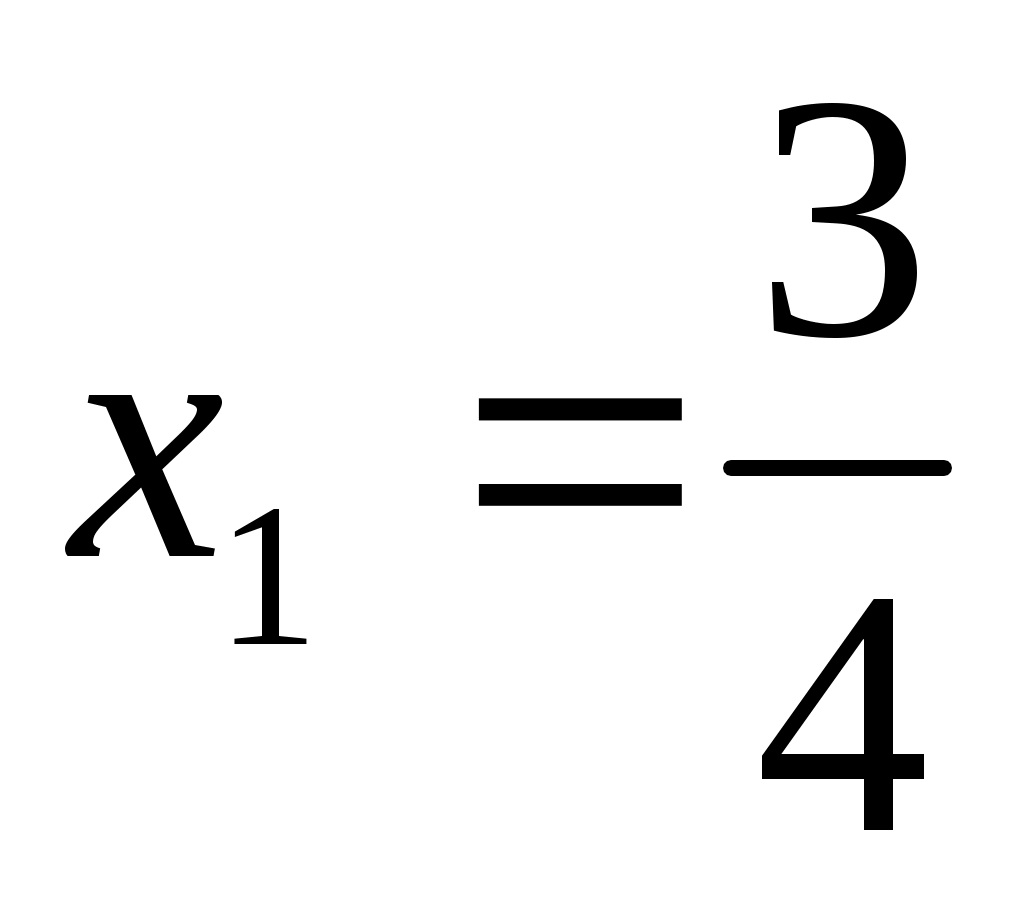 , , 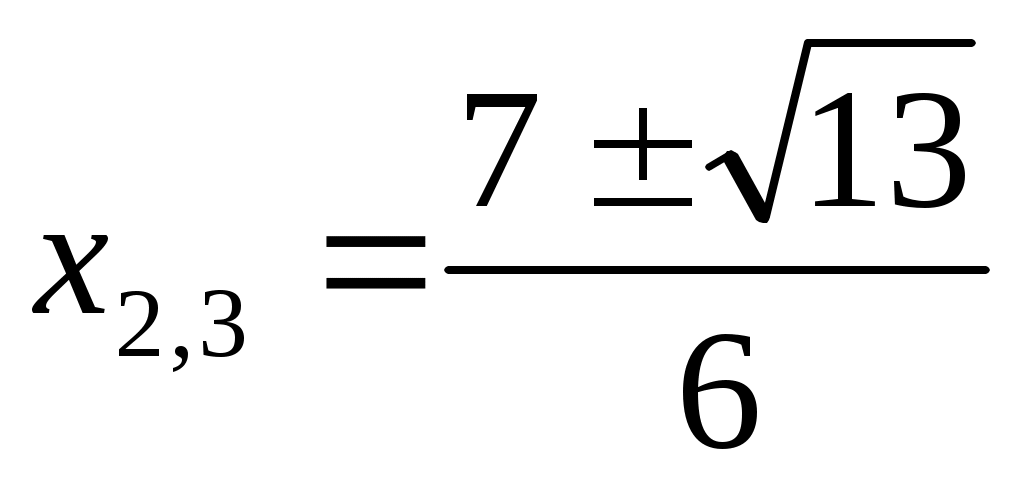 түбірлерін алдық. Тексеру түбірлерін алдық. Тексеру 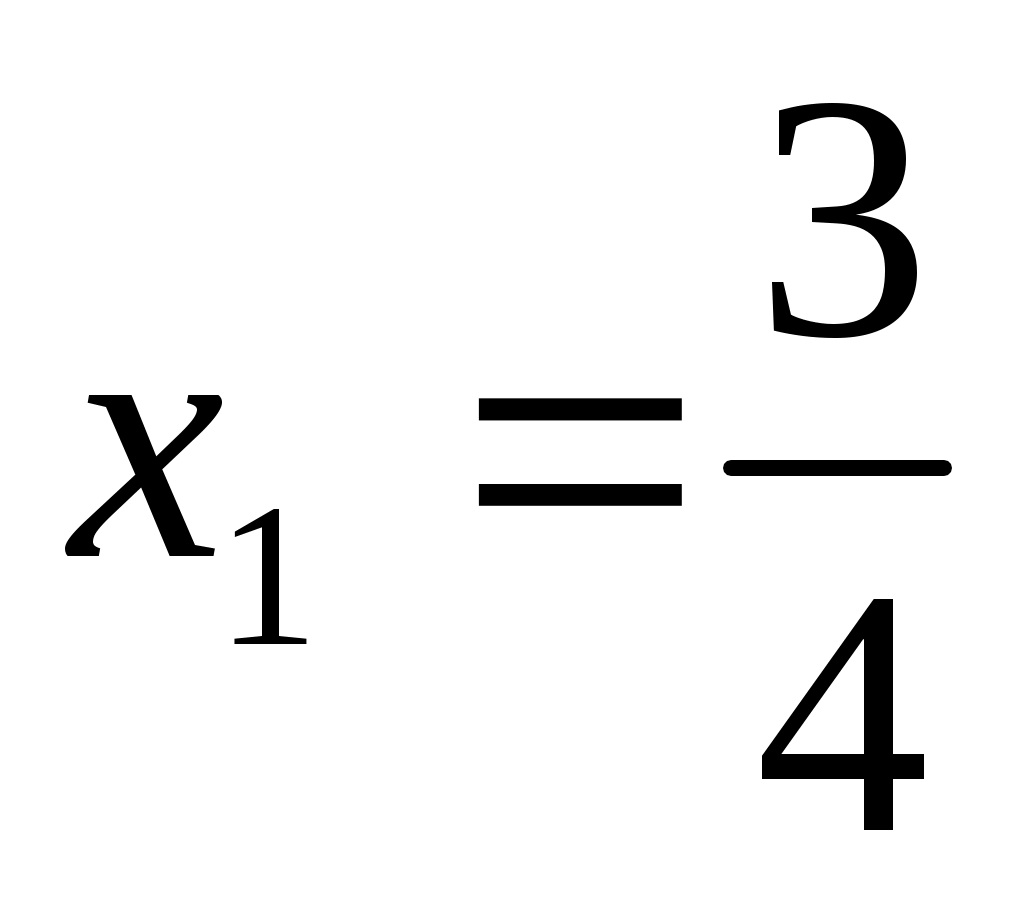 , , 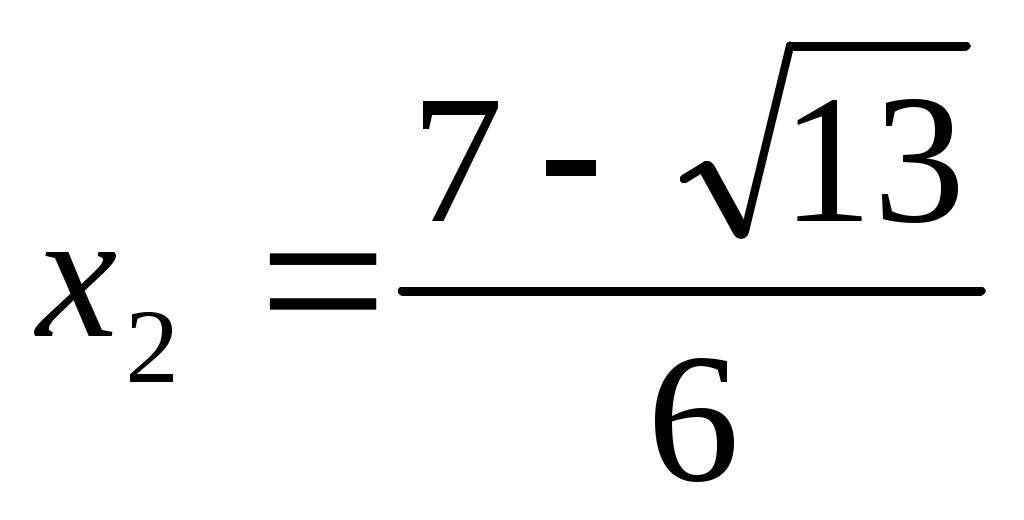 сандары (1) теңдеуге түбір болатынын көрсетеді. сандары (1) теңдеуге түбір болатынын көрсетеді.
Жауабы: 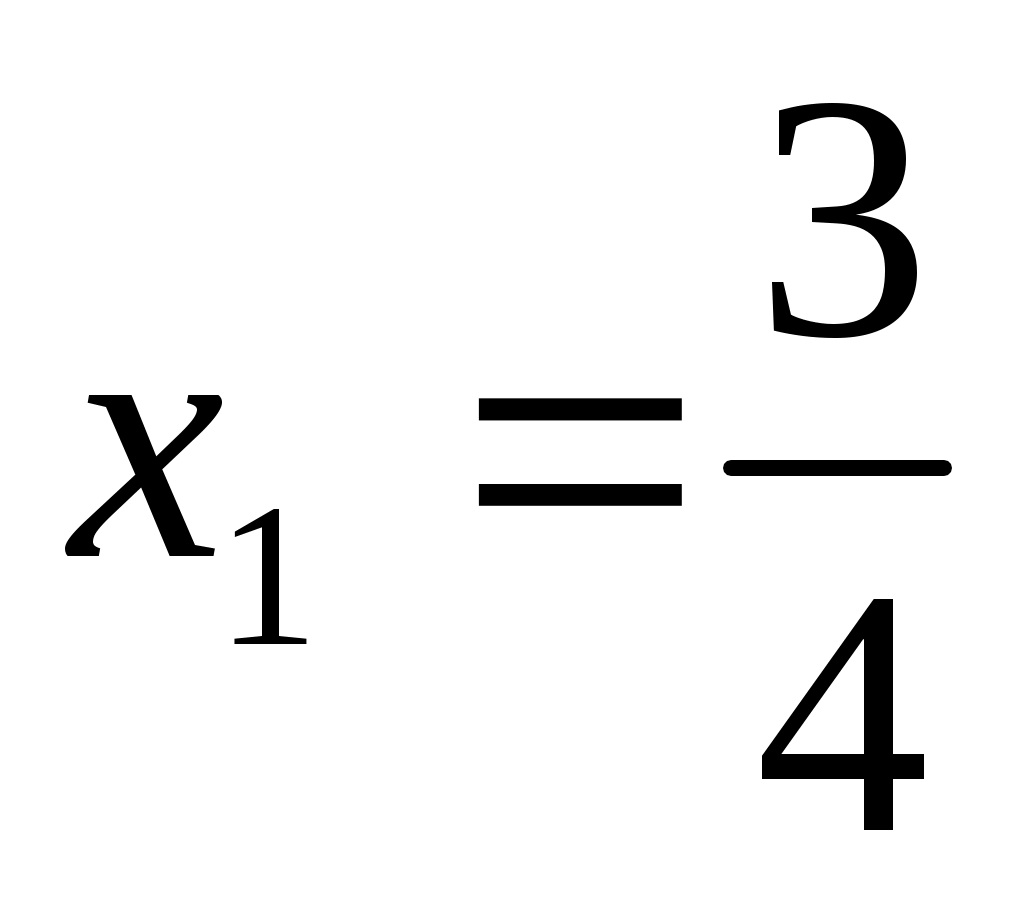 , , 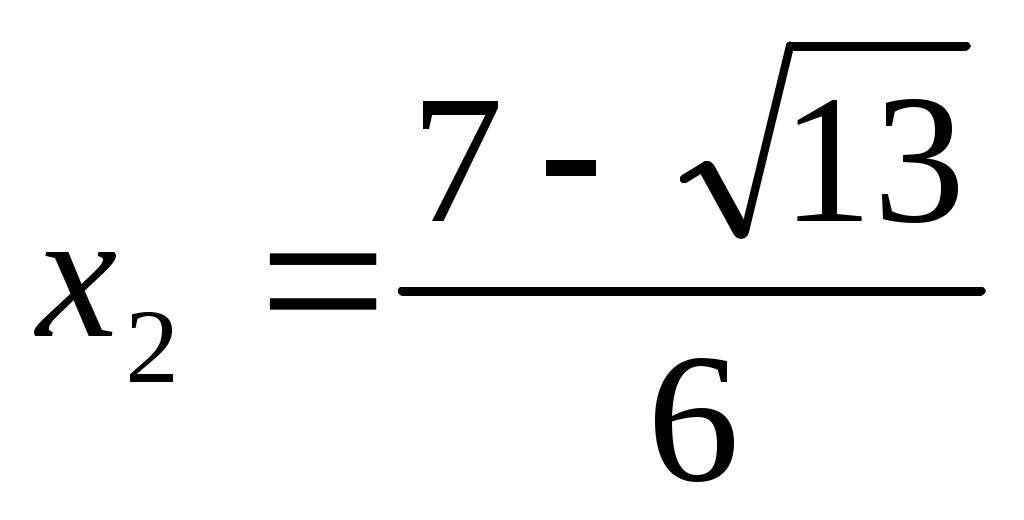
5-әдіс. Жаңа айнымалы енгізу арқылы рационал теңдеуге келтіріп шешу.
Көптеген иррационал теңдеулерді шешуде жаңа айнымалы енгізу тәсілі қолданылады. Бұл тәсіл кез келген күрделі теңдеуді қарапайым теңдеуге келтіріп, теңдеу шешуді жеңілдетеді.
Мысал 8. 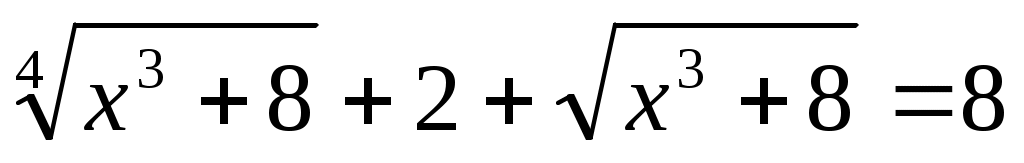 (1) (1)
Шешуі: 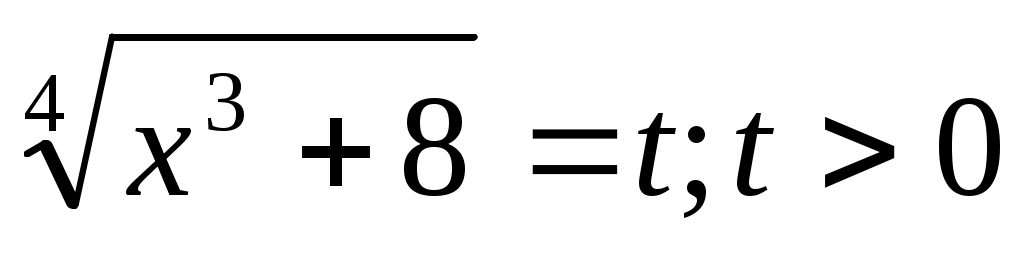 (2) белгілеуін енгізіп, (2) белгілеуін енгізіп, 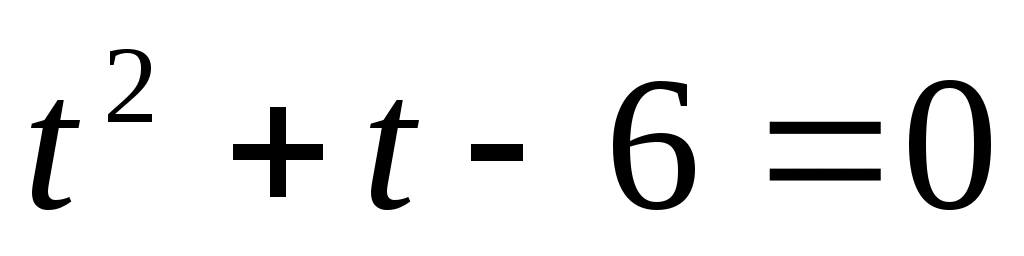 теңдеуін аламыз. Бұдан теңдеуін аламыз. Бұдан 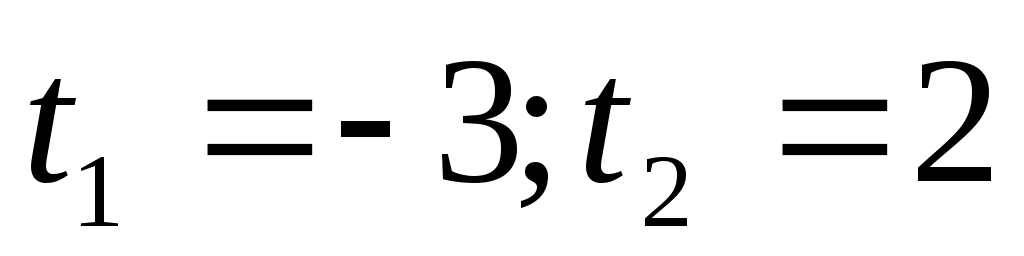 түбірлерін табамыз. түбірлерін табамыз. 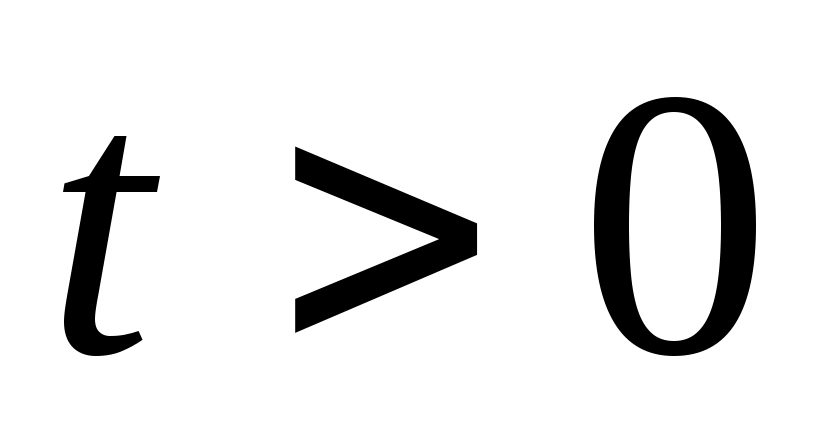 болатынын ескере отырып, болатынын ескере отырып, 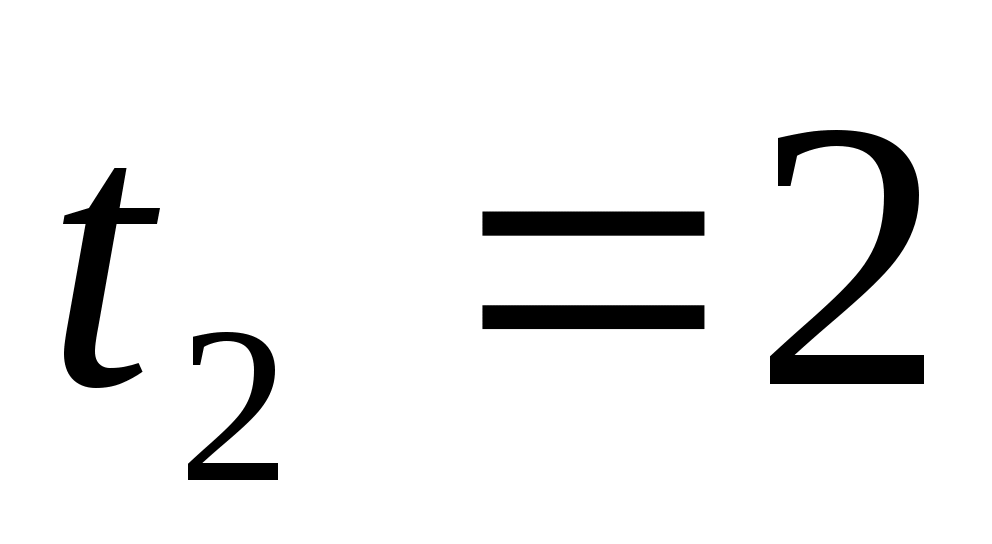 мәнін (2)-ге қойсақ, мәнін (2)-ге қойсақ, 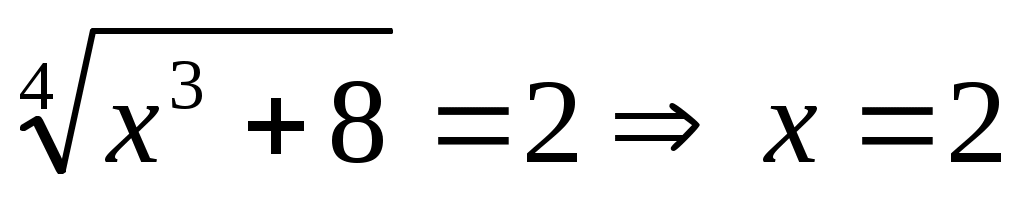 шешімін аламыз. шешімін аламыз.
Жауабы: 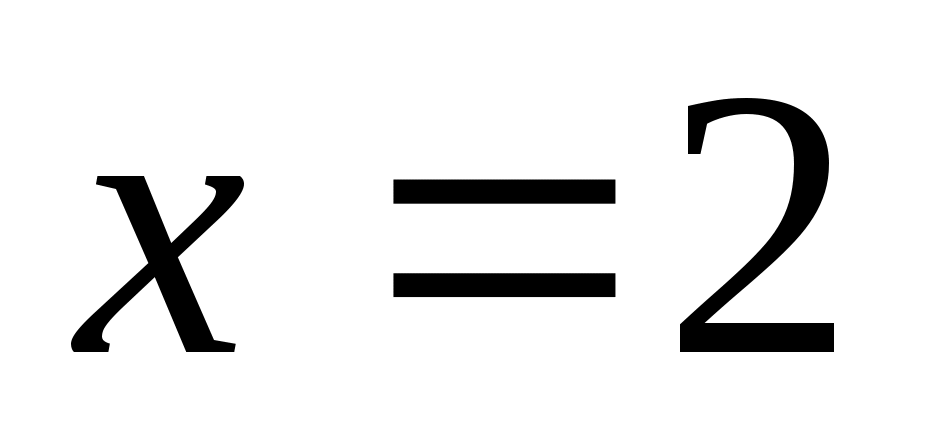
Мысал 9. 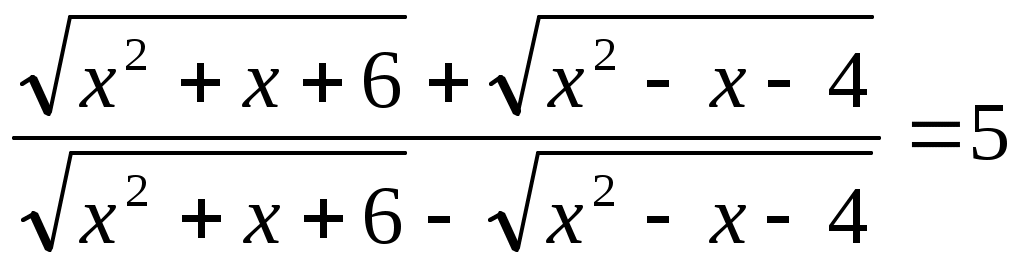 (1) (1)
Шешуі:
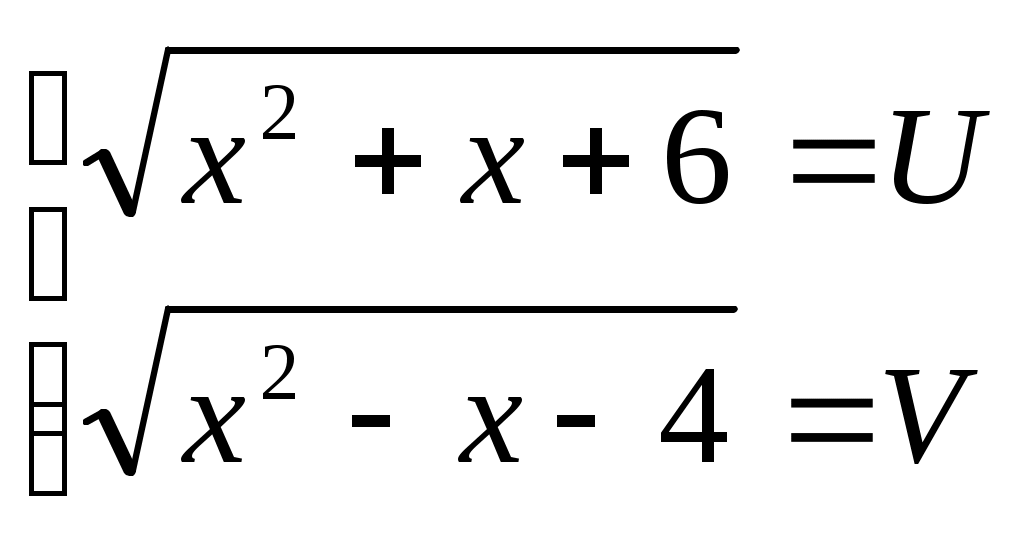 (2) белгілеуін енгізсек, теңдеудің жазылуы әлдеқайда ықшамдалады. (2) белгілеуін енгізсек, теңдеудің жазылуы әлдеқайда ықшамдалады.
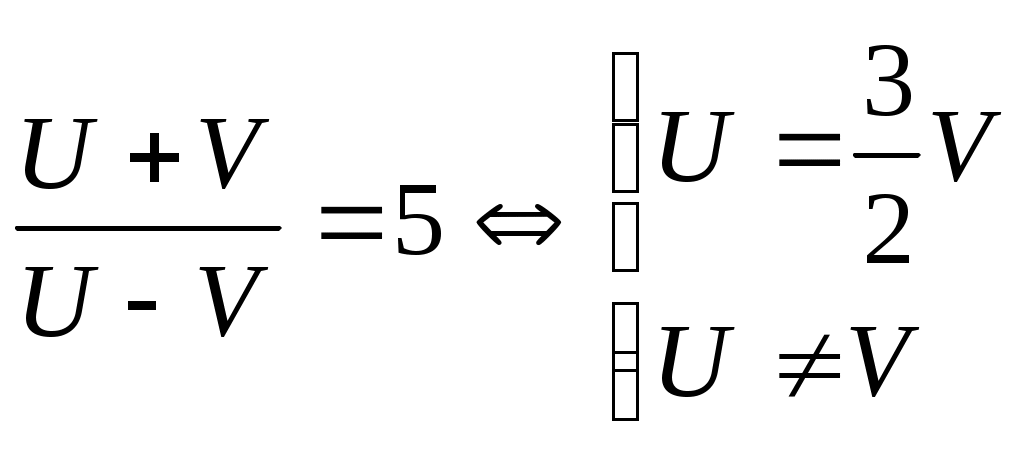 . Осы табылған мәнді (2) дегі орнына қойсақ, . Осы табылған мәнді (2) дегі орнына қойсақ, 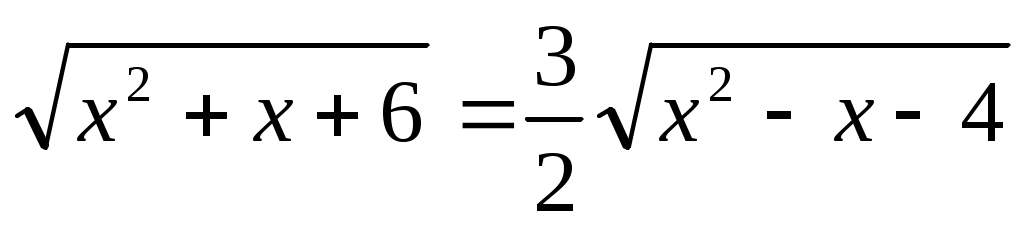 теңдеуін аламыз. Екі жағын квадраттай отырып, теңдеуін аламыз. Екі жағын квадраттай отырып, 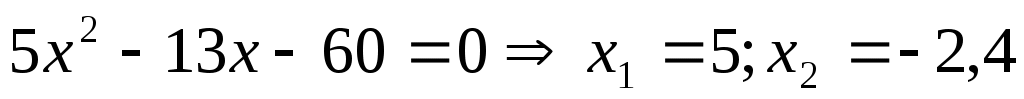 теңдеудің шешімін аламыз. Тексеру арқылы (1) теңдеуге табылған екі мәннің де шешім болатынын анықтаймыз. теңдеудің шешімін аламыз. Тексеру арқылы (1) теңдеуге табылған екі мәннің де шешім болатынын анықтаймыз.
Жауабы: 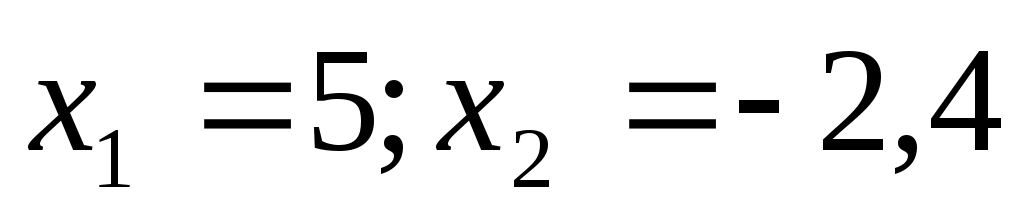
Мысал 10. 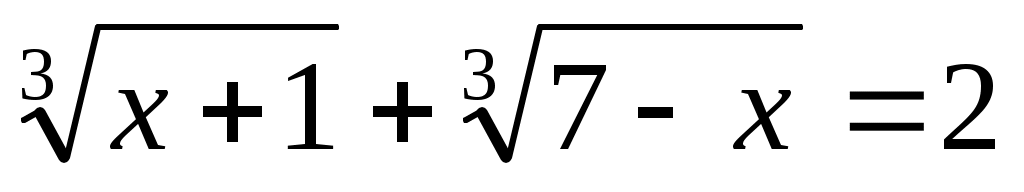 (1) (1)
Шешуі: 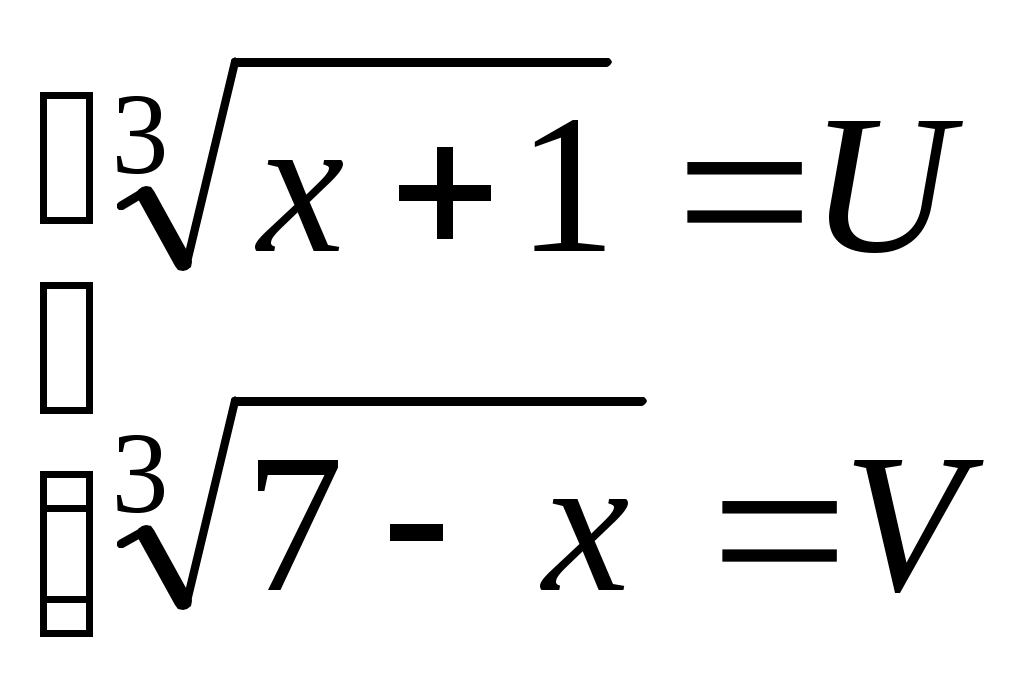 (2) белгілеуін енгізсек, (1) теңдеуі (2) белгілеуін енгізсек, (1) теңдеуі 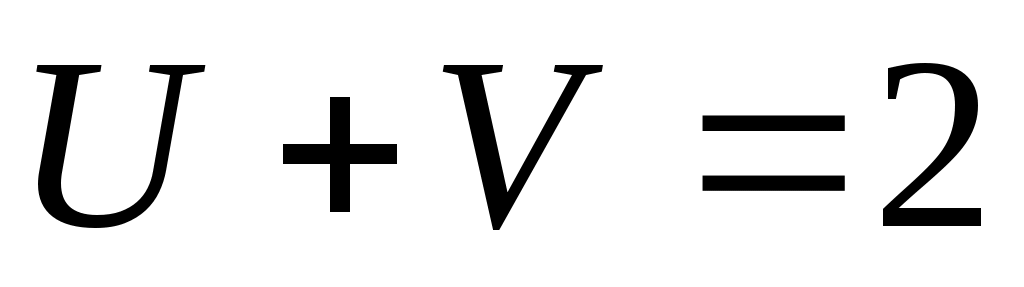 түріне келеді. (2) жүйедегі әрбір теңдеудің екі бөлігін кубтай отырып, түріне келеді. (2) жүйедегі әрбір теңдеудің екі бөлігін кубтай отырып, 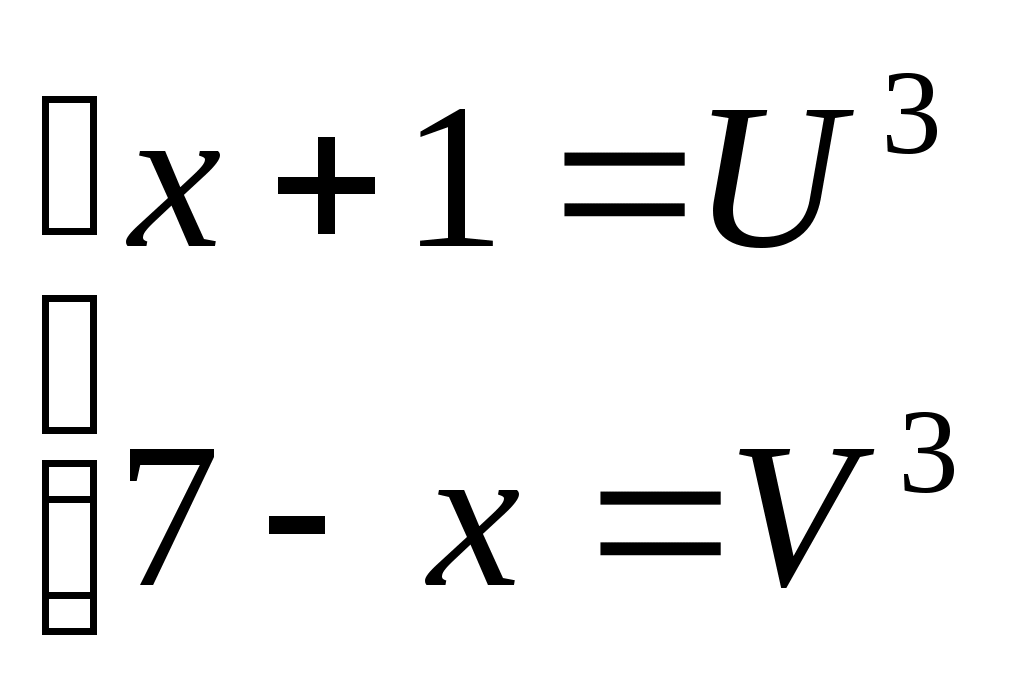 жүйесін аламыз. Жүйенің теңдеулерін мүшелеп қоссақ, жүйесін аламыз. Жүйенің теңдеулерін мүшелеп қоссақ, 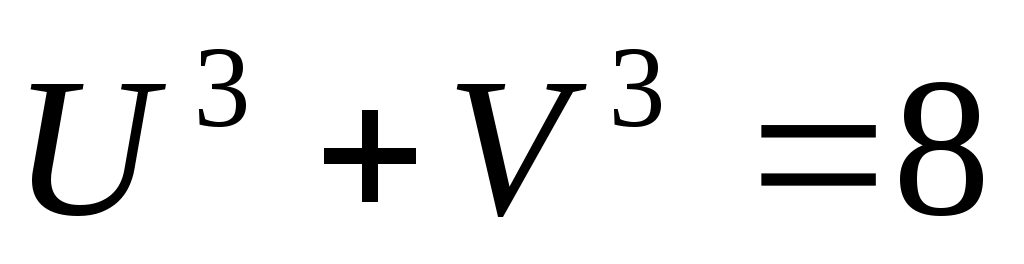 теңдеуін аламыз. Осылайша теңдеуін аламыз. Осылайша 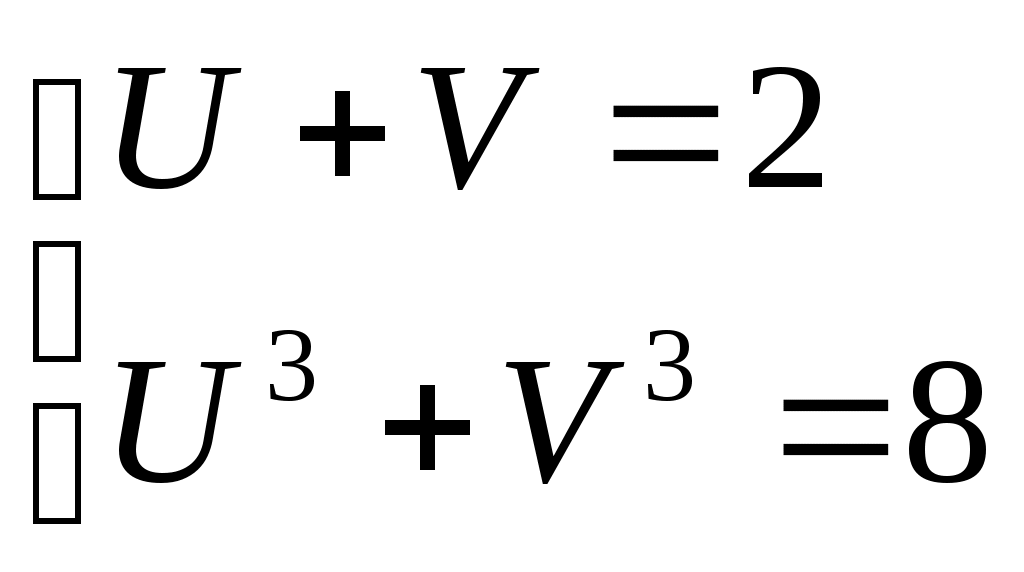 екі белгісізі бар жүйені шешеміз. Бұдан екі белгісізі бар жүйені шешеміз. Бұдан 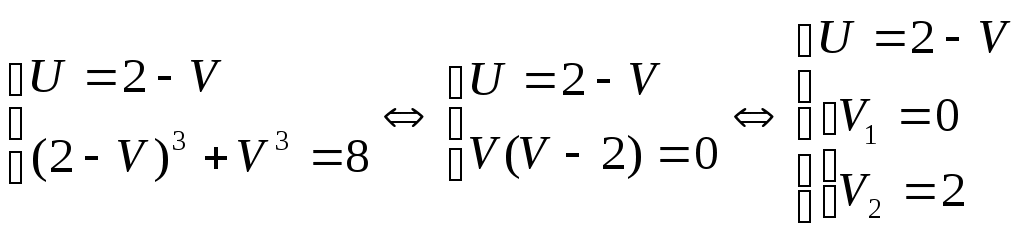 . Бұдан . Бұдан 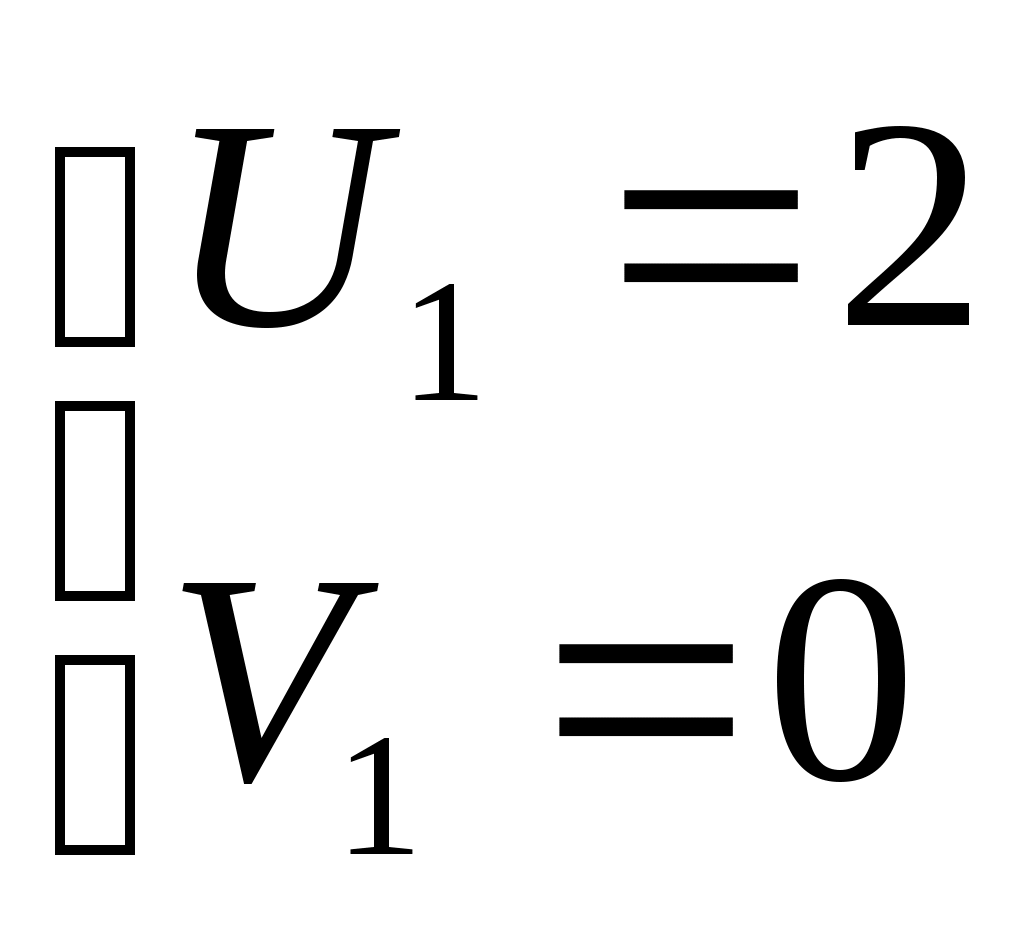 немесе немесе 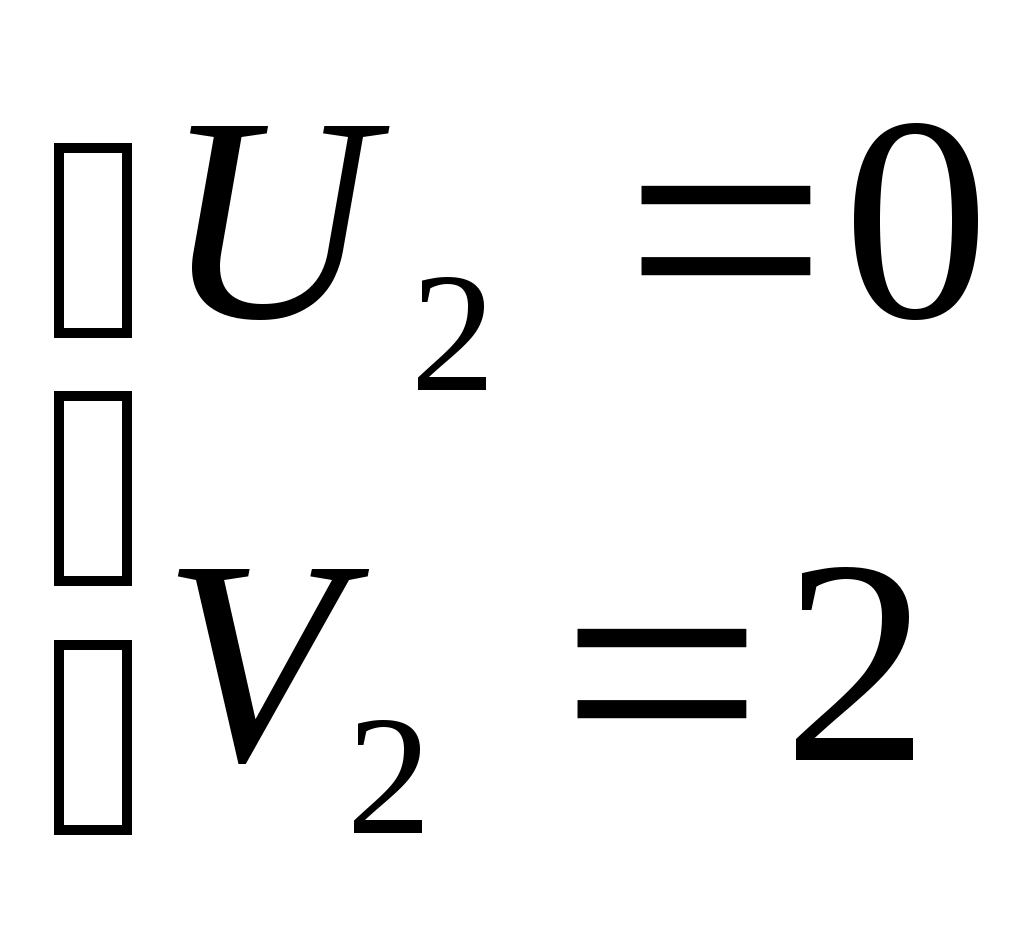 . Осылайша есеп келесі жүйелер жиынтығын шешуге келтіріледі: . Осылайша есеп келесі жүйелер жиынтығын шешуге келтіріледі: 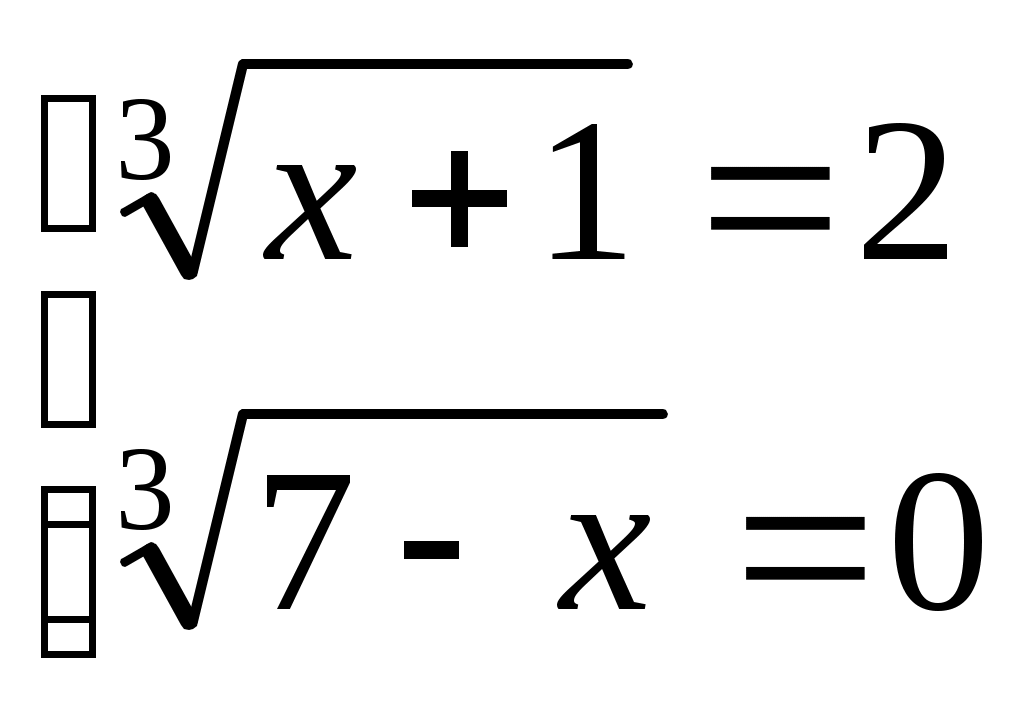 немесе немесе 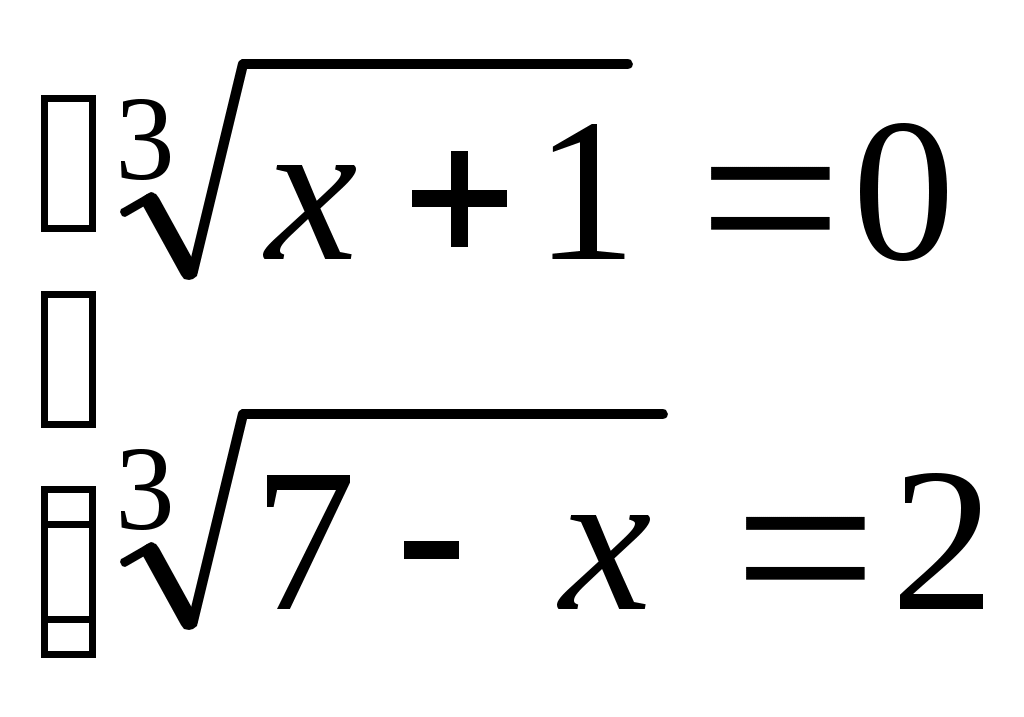 . Бұдан . Бұдан 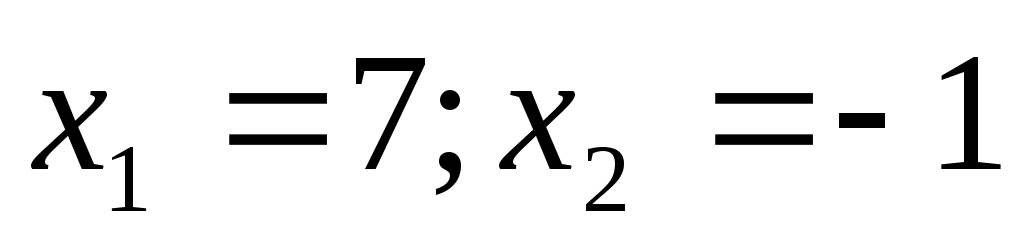 . Тексеру арқылы табылған түбірлер (1) теңдеуінің шешімдері болатынын көреміз. . Тексеру арқылы табылған түбірлер (1) теңдеуінің шешімдері болатынын көреміз.
Жауабы: 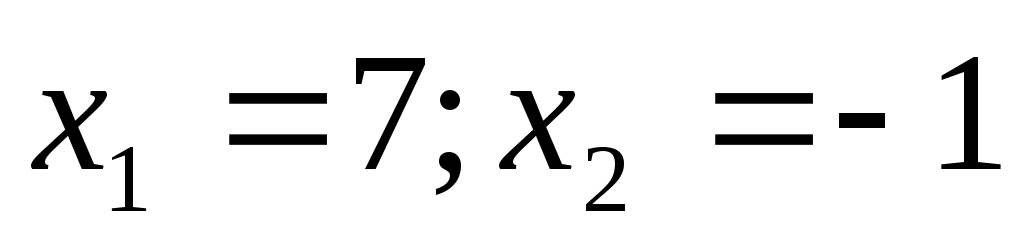
Мысал 11. 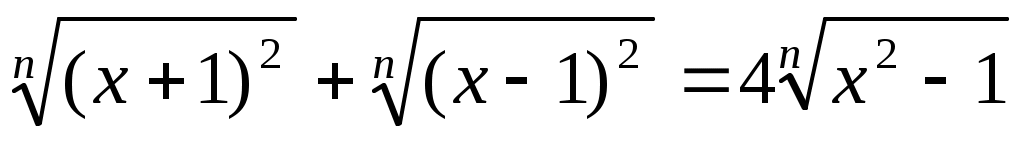 (1) (1)
Шешуі: 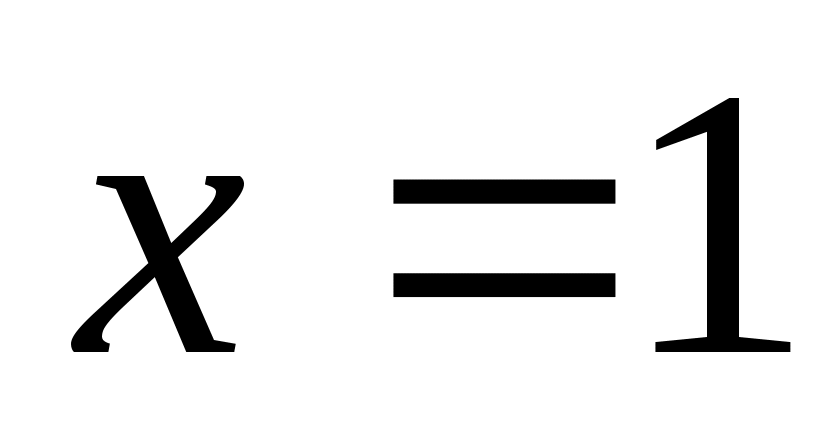 мәні берілген теңдеудің түбірі болмайтындықтан, мәні берілген теңдеудің түбірі болмайтындықтан, 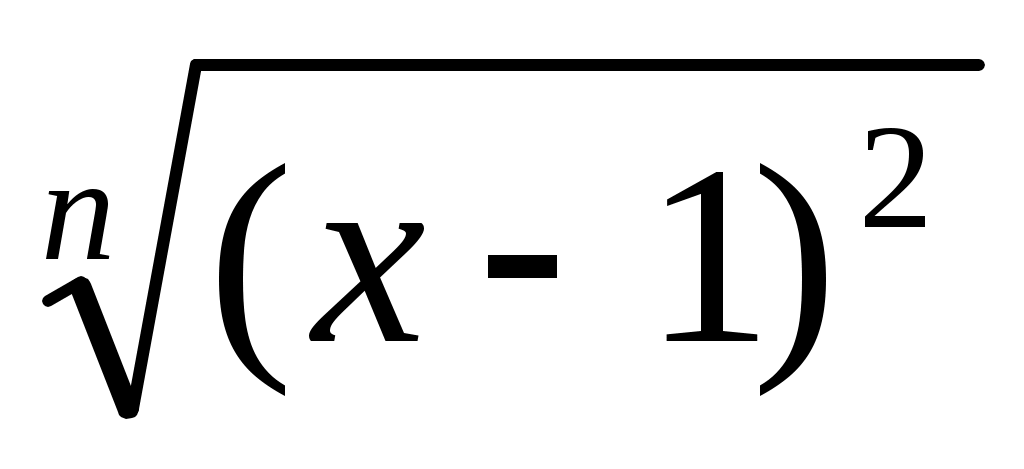 өрнегіне теңдеудің екі бөлігін де бөлеміз. Сонда (1)-ге мәндес өрнегіне теңдеудің екі бөлігін де бөлеміз. Сонда (1)-ге мәндес 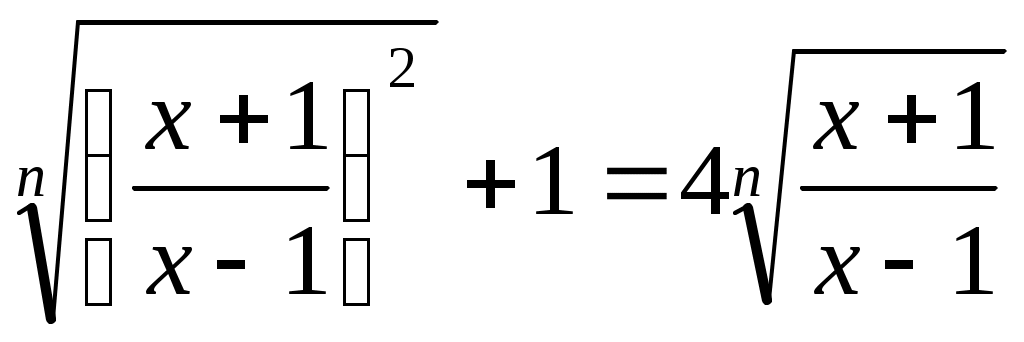 (2) теңдеуі шығады. (2) теңдеуі шығады. 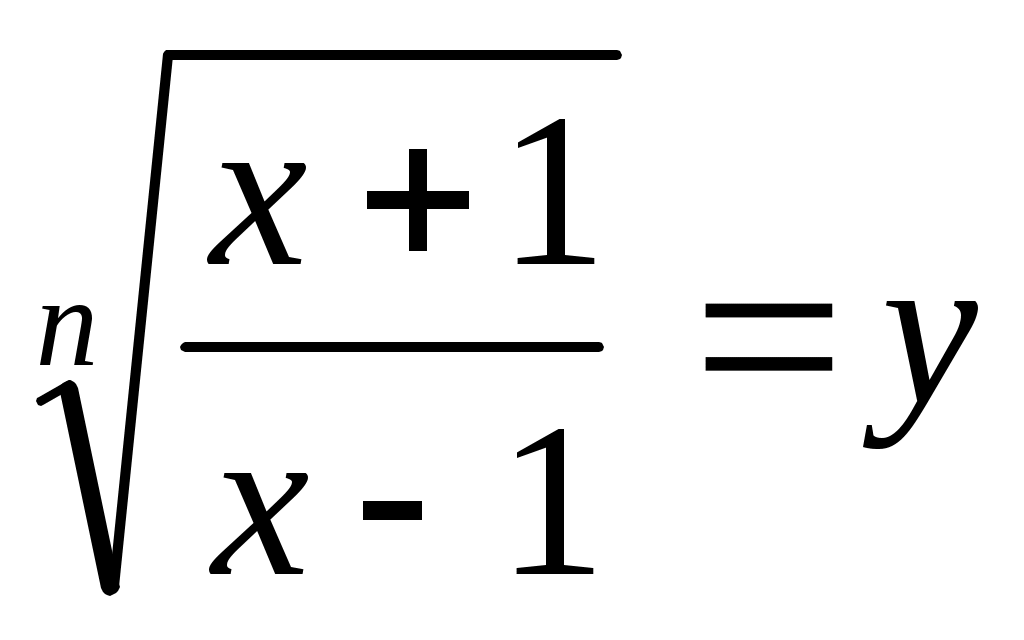 белгілеуін енгізіп, (2) теңдеуден белгілеуін енгізіп, (2) теңдеуден 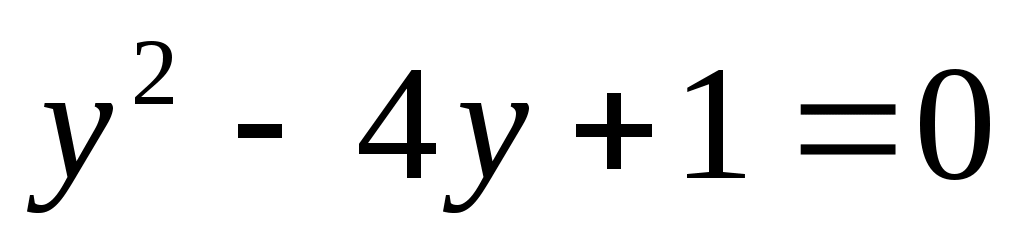 теңдеуін аламыз. Бұдан теңдеуін аламыз. Бұдан 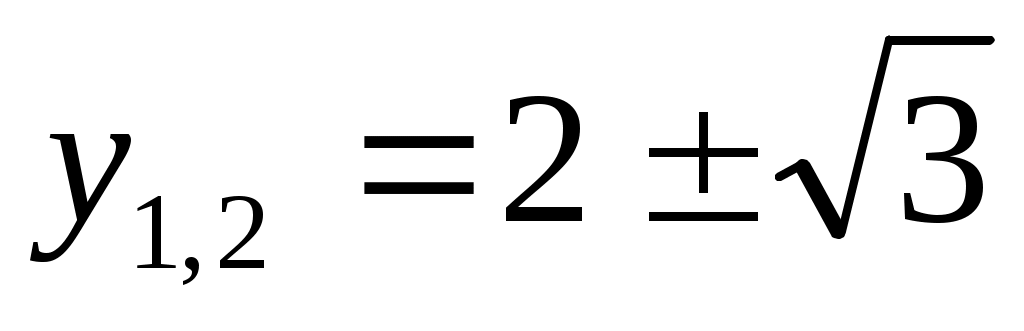 . .
Сонда белгілеудегі орнына қойсақ, 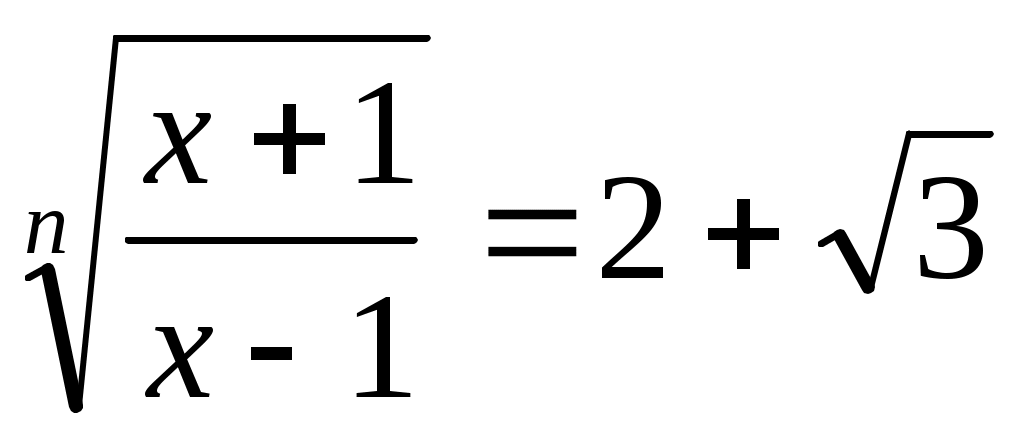 ; ; 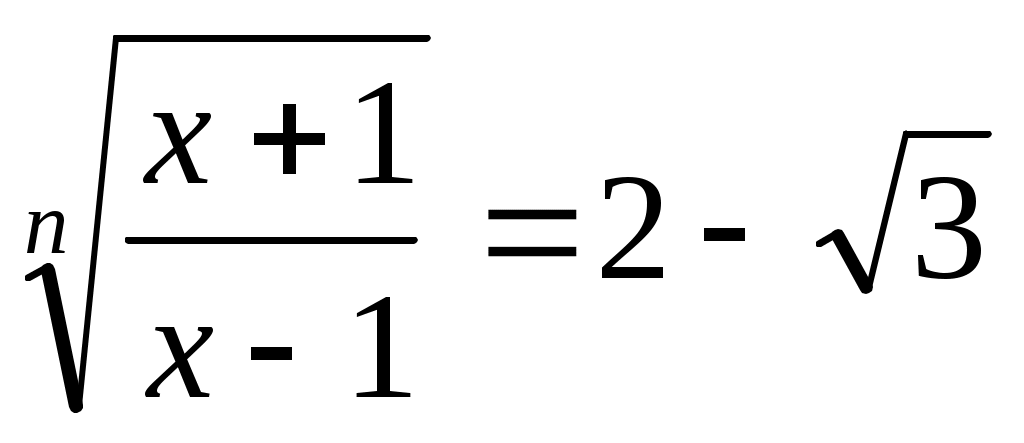 (3). (3).
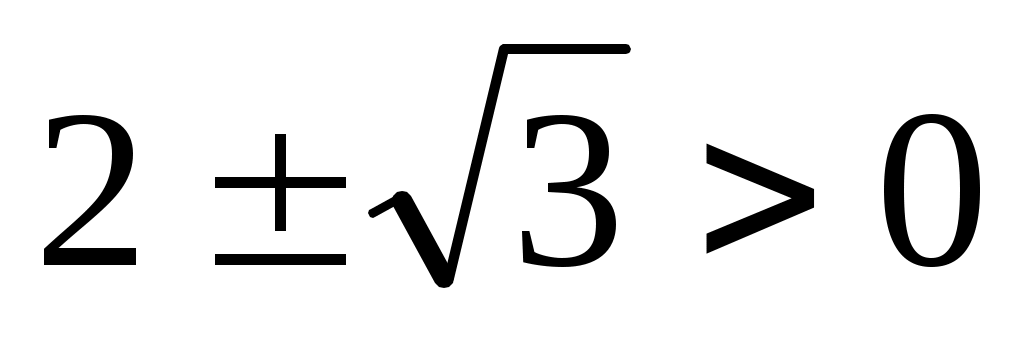 болғандықтан теңдеудің екі бөлігін болғандықтан теңдеудің екі бөлігін 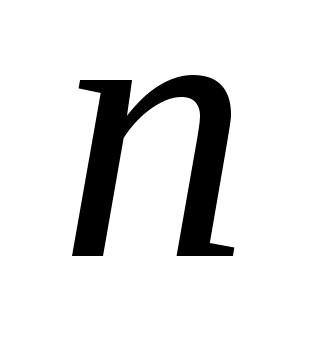 дәрежеге шығарамыз. Яғни дәрежеге шығарамыз. Яғни 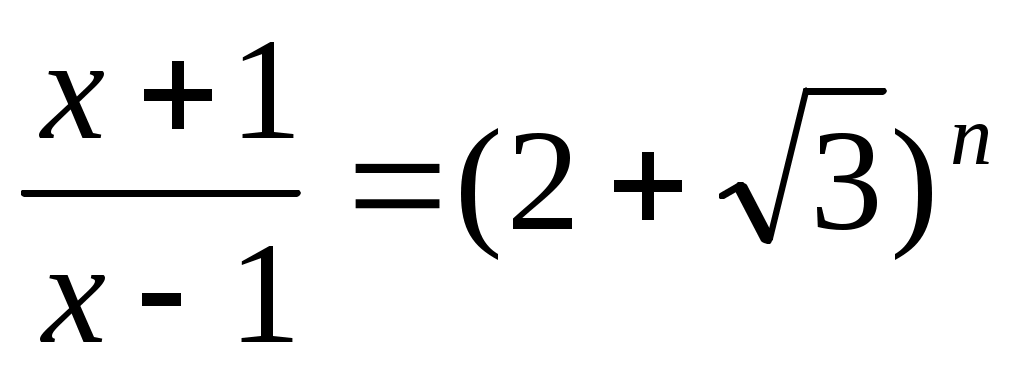 немесе немесе 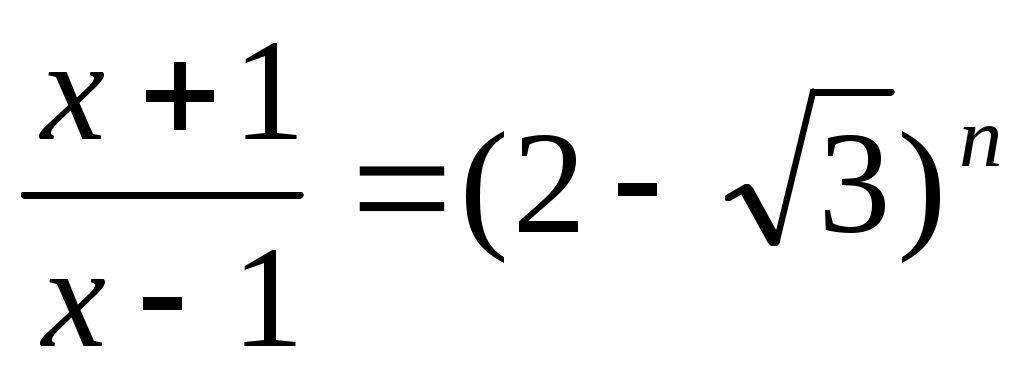 (4). Бұдан (4). Бұдан 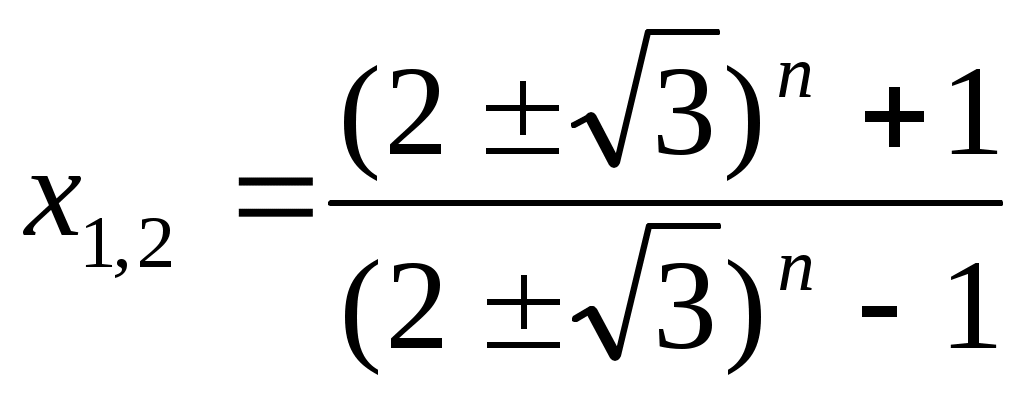 түбірлерін табамыз. (1), (2), (3), (4) теңдеулері мәндес болғандықтан, бұл түбірлер (1) теңдеуге шешім болады. түбірлерін табамыз. (1), (2), (3), (4) теңдеулері мәндес болғандықтан, бұл түбірлер (1) теңдеуге шешім болады.
Жауабы: 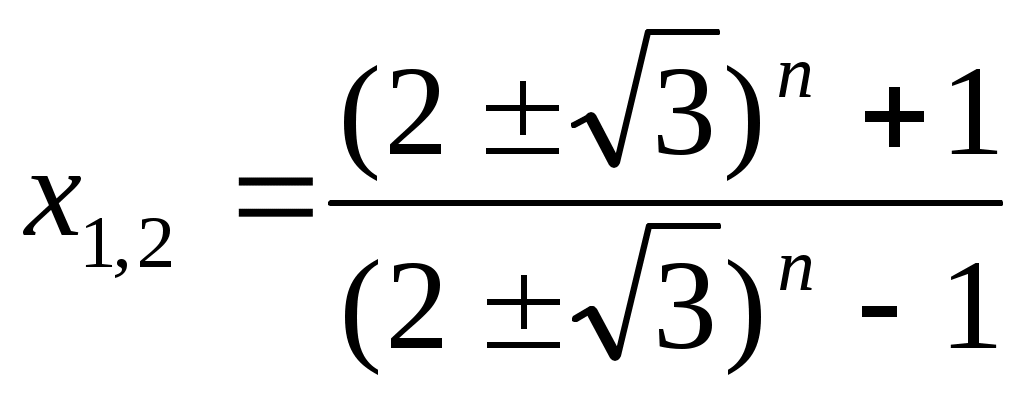
Енді параметрі бар иррационал теңдеулерге мысалдар келтірейік.
Мысал 12. 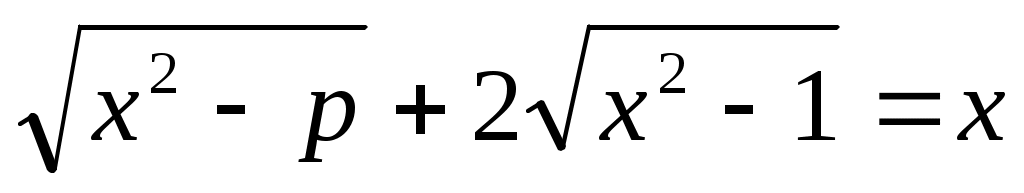 (1) (1)
Шешуі: Теңдеудің екі бөлігін екі рет квадраттай отырып, 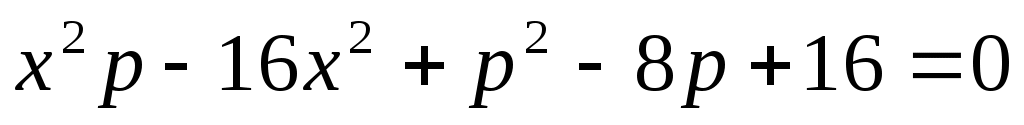 . Бұдан . Бұдан 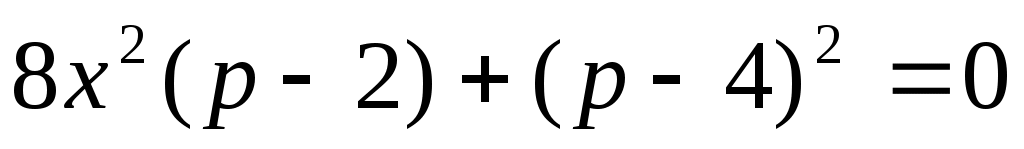 (2). Бұдан (2). Бұдан 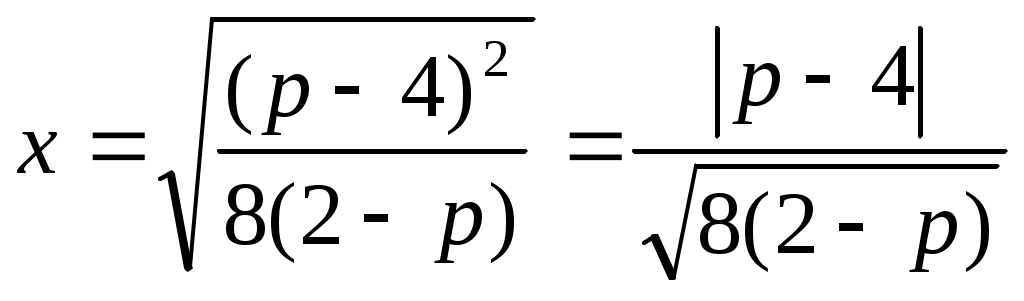 . Енді осы табылған түбірдегі р параметрінің қабылдайтын мәндеріне тоқталайық. Арифметикалық квадрат түбірдің және бөлшектің мағынасы болуы үшін . Енді осы табылған түбірдегі р параметрінің қабылдайтын мәндеріне тоқталайық. Арифметикалық квадрат түбірдің және бөлшектің мағынасы болуы үшін 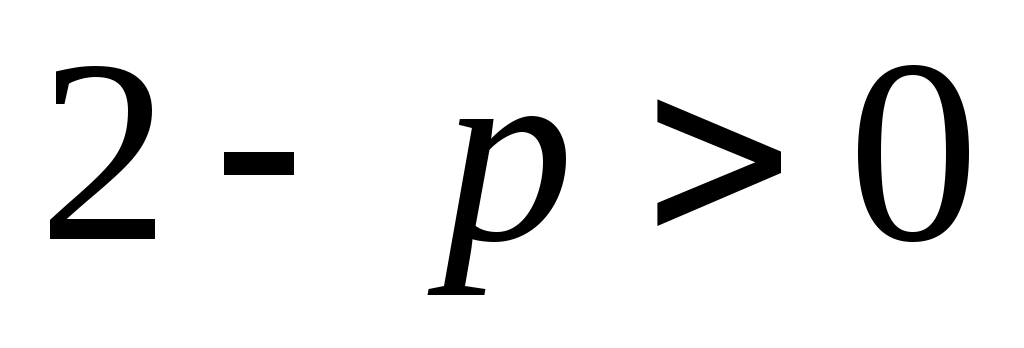 болуы керек. Яғни болуы керек. Яғни 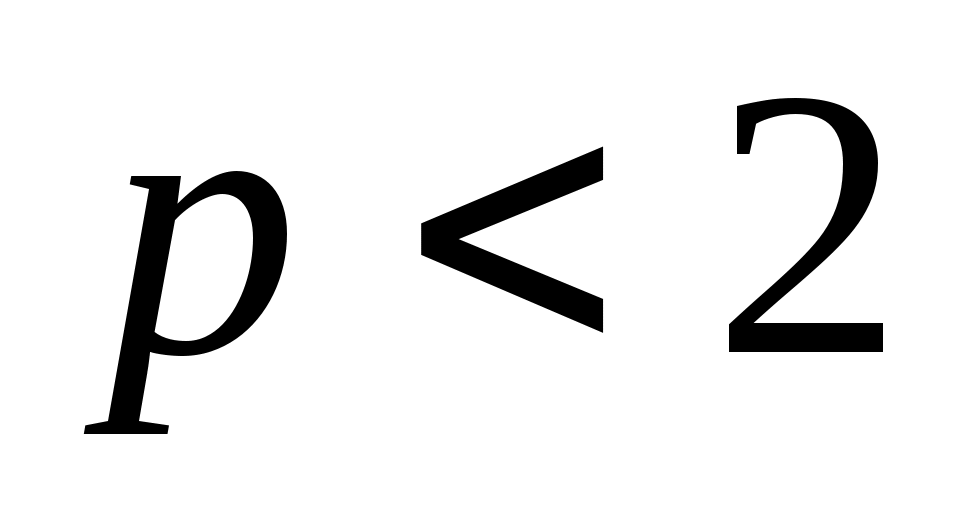 мәндері үшін мәндері үшін 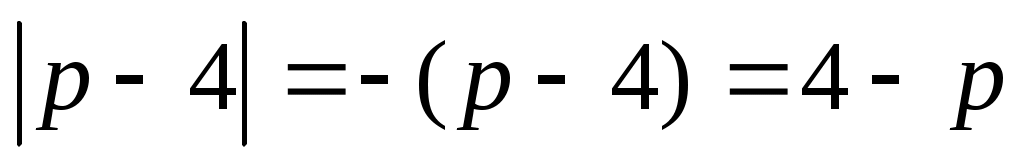 болатынын ескерсек, болатынын ескерсек, 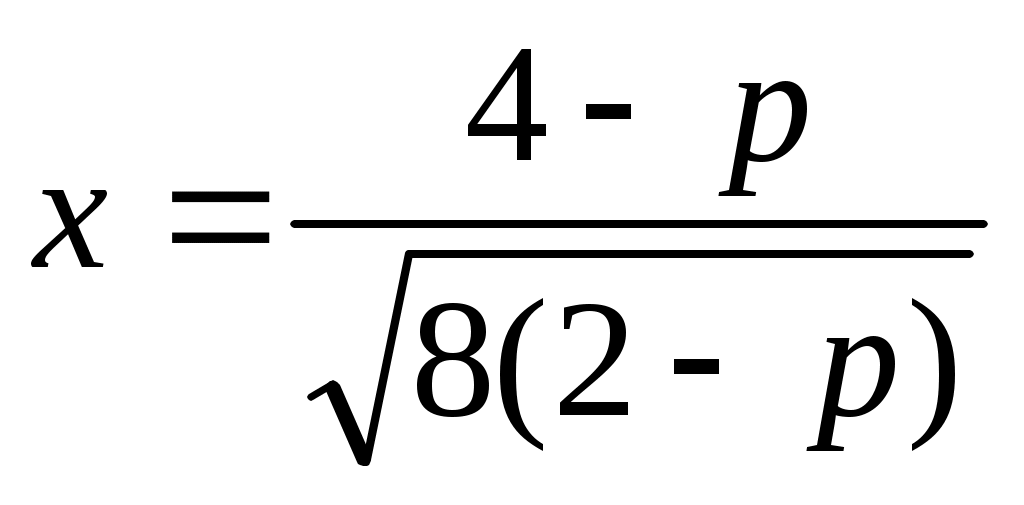 түбірін аламыз. Ал, түбірін аламыз. Ал, 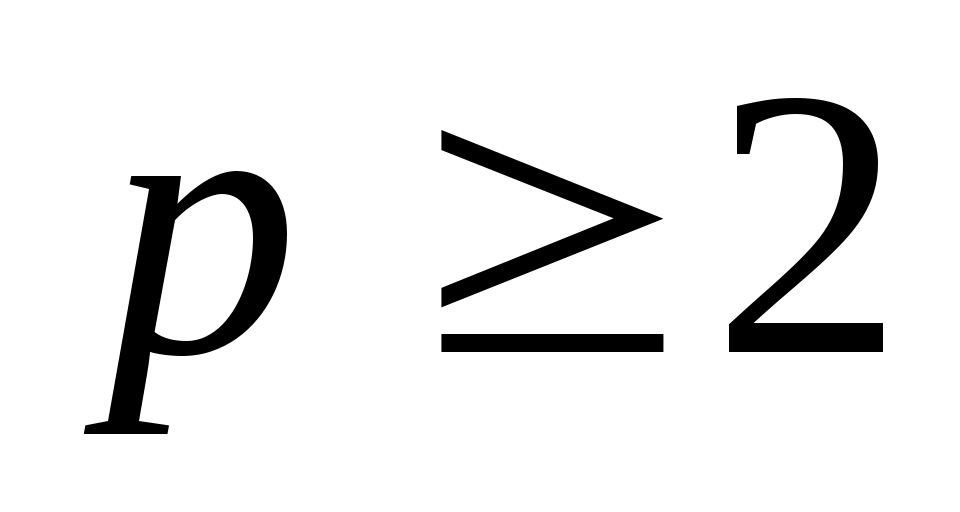 болғанда х-тің мәні анықталмайды, яғни теңдеудің түбірі болмайды. (1) мен (2) теңдеулер х≥0 болғанда мәндес. Сондықтан табылған түбір (1) теңдеуіне де шешім болады. болғанда х-тің мәні анықталмайды, яғни теңдеудің түбірі болмайды. (1) мен (2) теңдеулер х≥0 болғанда мәндес. Сондықтан табылған түбір (1) теңдеуіне де шешім болады.
Жауабы: 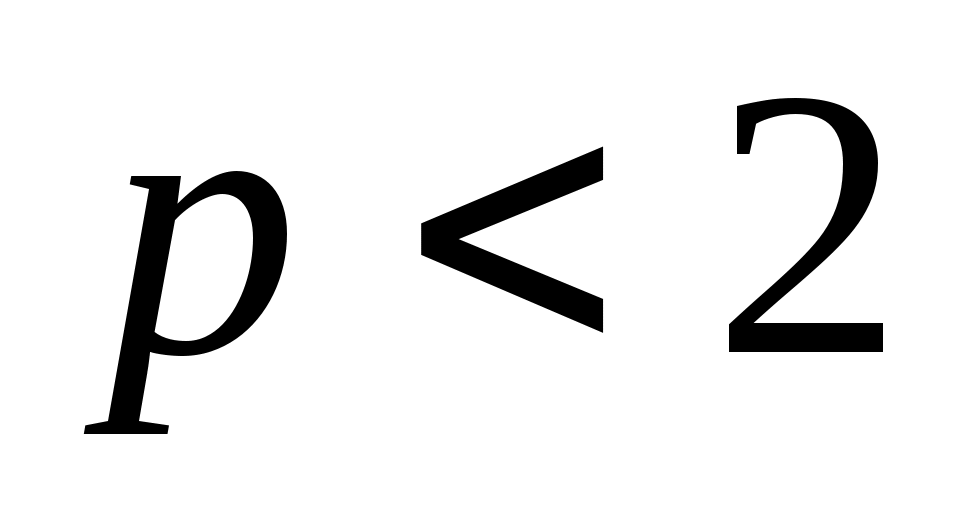 болғанда болғанда 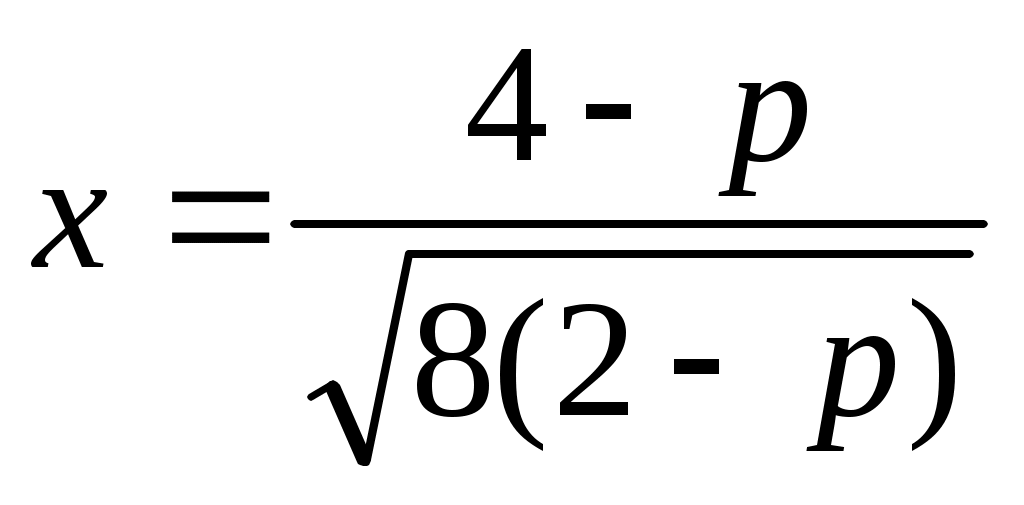 ; ;
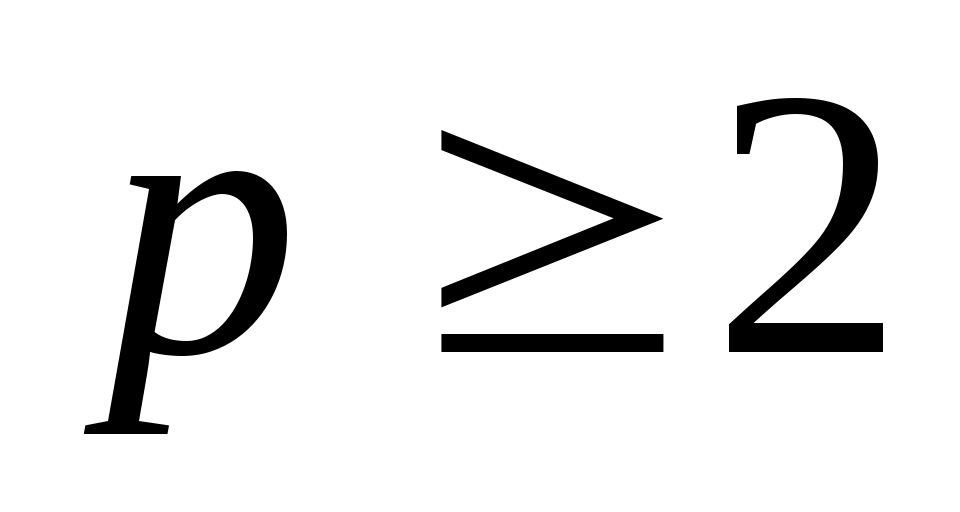 болғанда шешімі жоқ болғанда шешімі жоқ
Мысал 13. 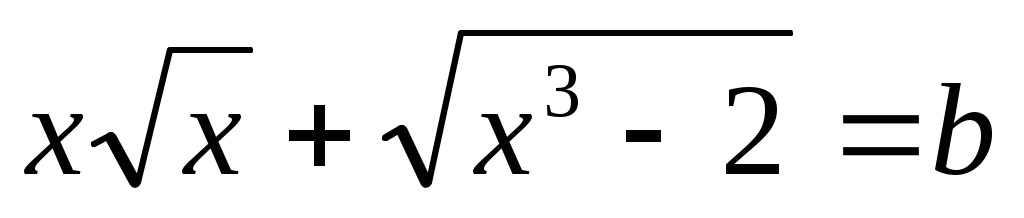 (1) (1)
Шешуі: (1) теңдеудің ММО: 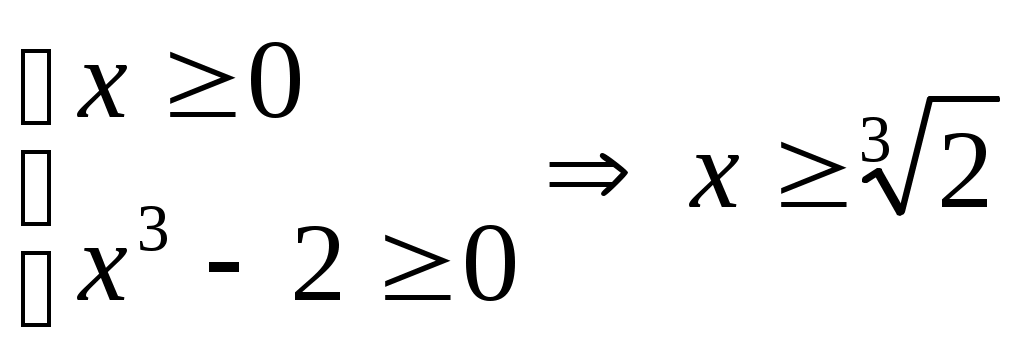 , яғни , яғни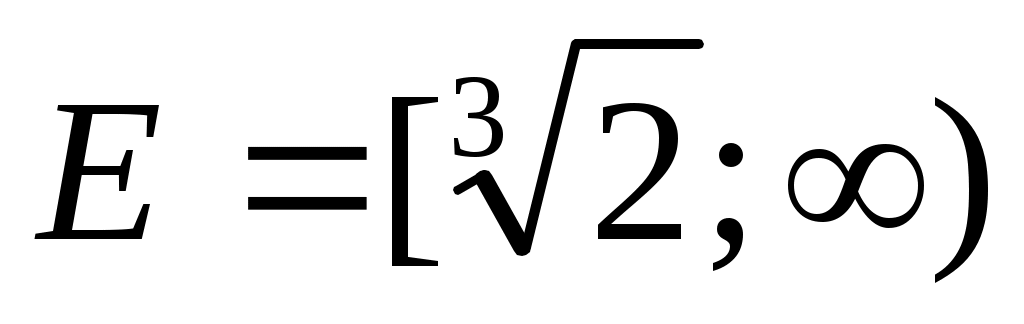 . .
Теңдеуді 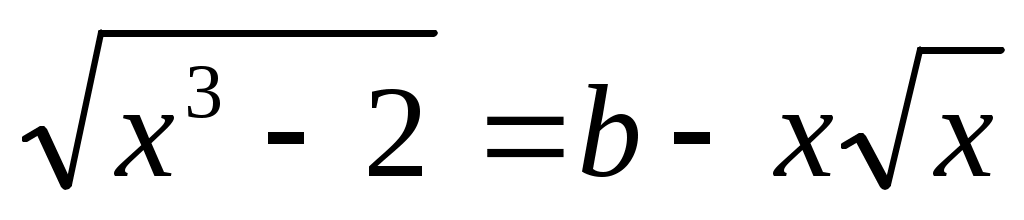 түрінде жазып, екі бөлігін квадраттаймыз. Сонда түрінде жазып, екі бөлігін квадраттаймыз. Сонда 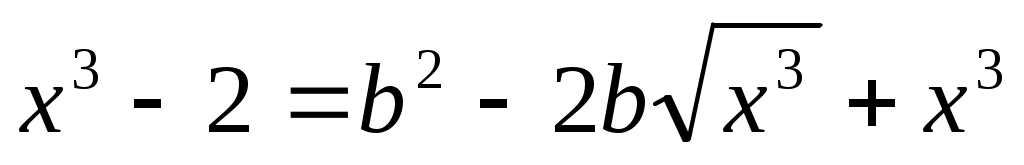 (2) теңдеуі шығады. Бұдан (2) теңдеуі шығады. Бұдан 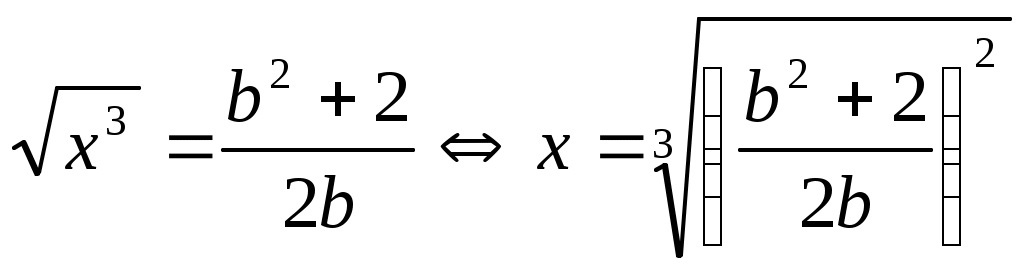 . . 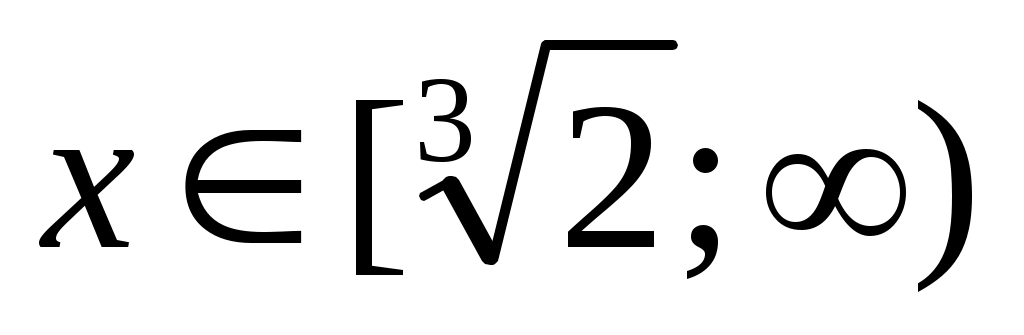 болғанда болғанда 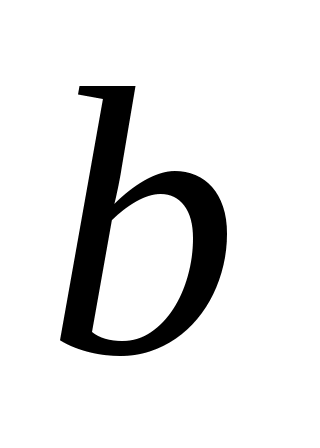 параметрінің бақылау мәнін табайық. параметрінің бақылау мәнін табайық. 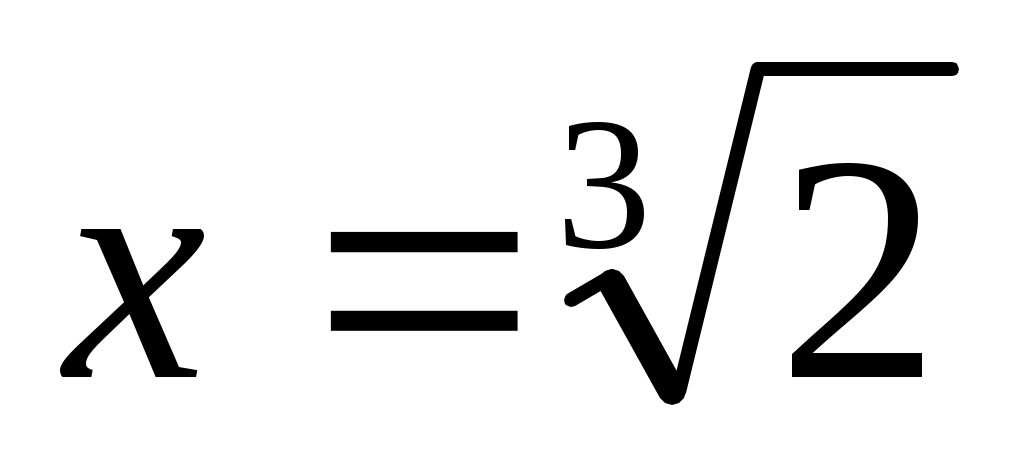 болғанда болғанда 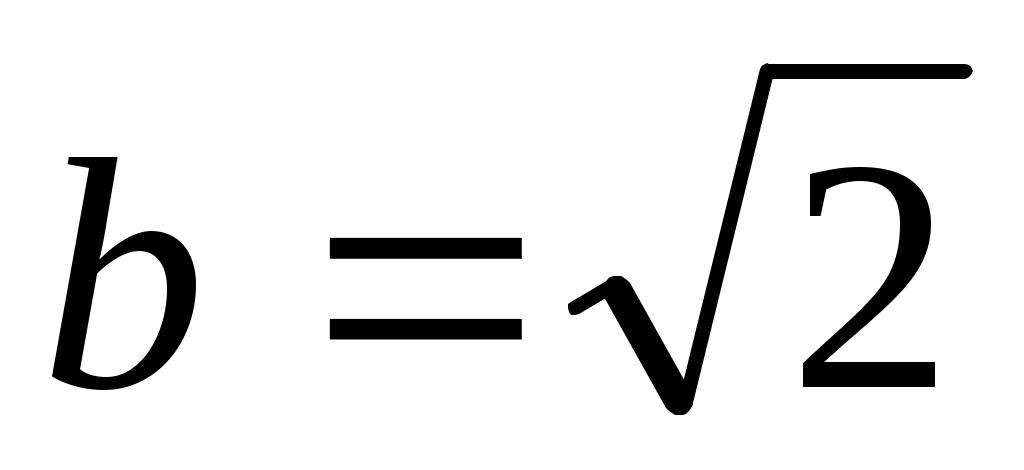 . Ал осыдан . Ал осыдан 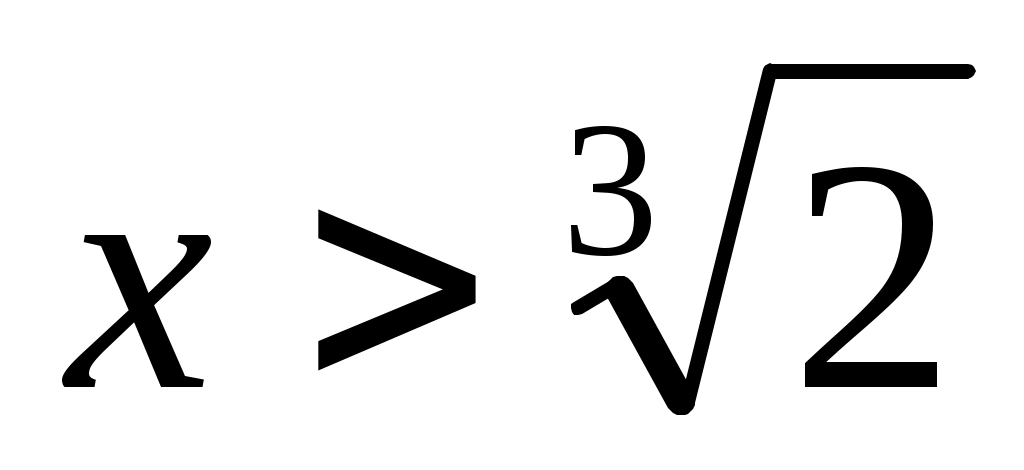 болғанда болғанда 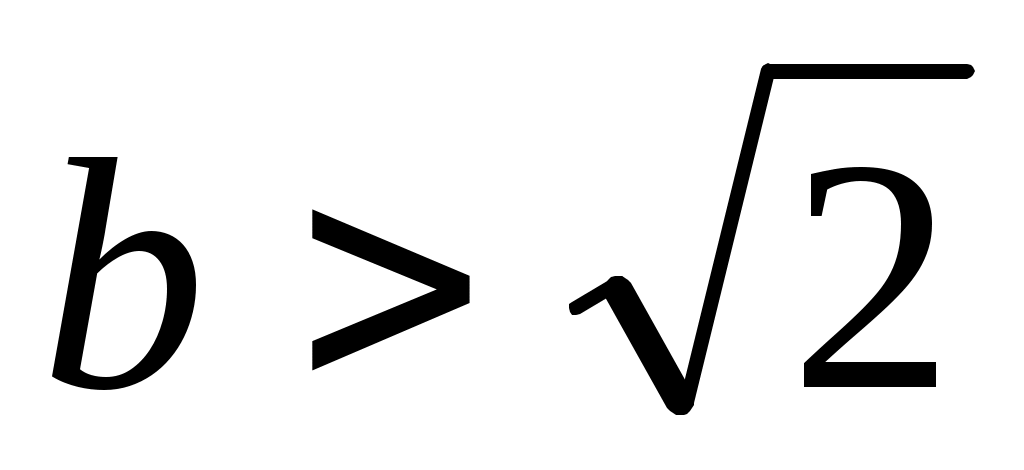 болады. болады.
Демек, (2) теңдеудің шешімі 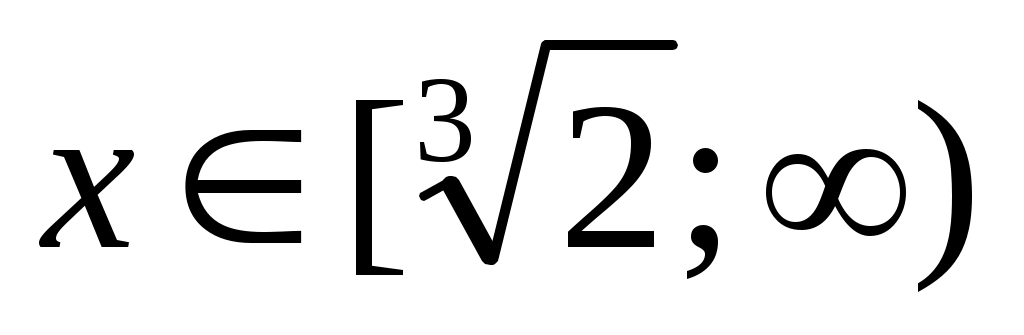 және және 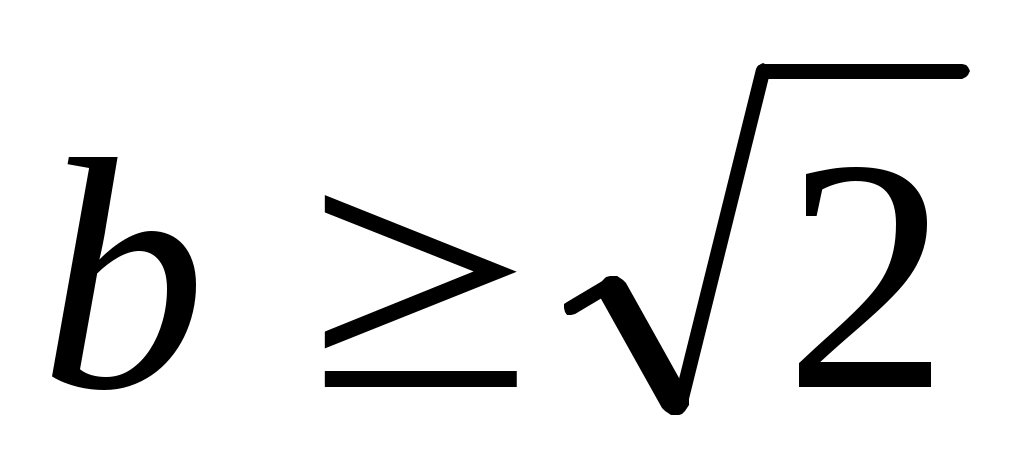 болғанда болғанда 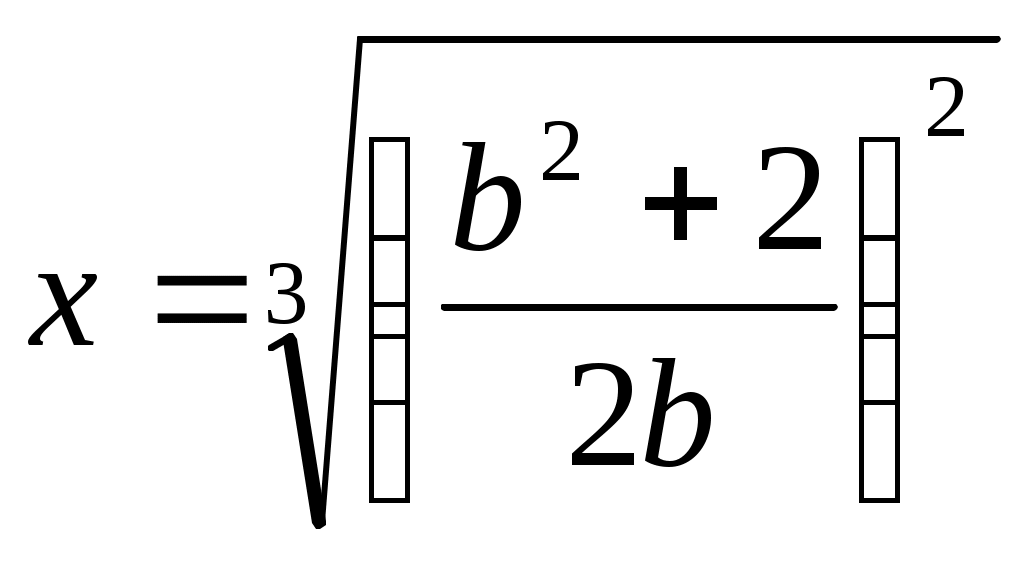 болады. Бұл түбір ММО-да (2)-ге мәндес (1) теңдеуге де шешім болады. болады. Бұл түбір ММО-да (2)-ге мәндес (1) теңдеуге де шешім болады.
Жауабы: 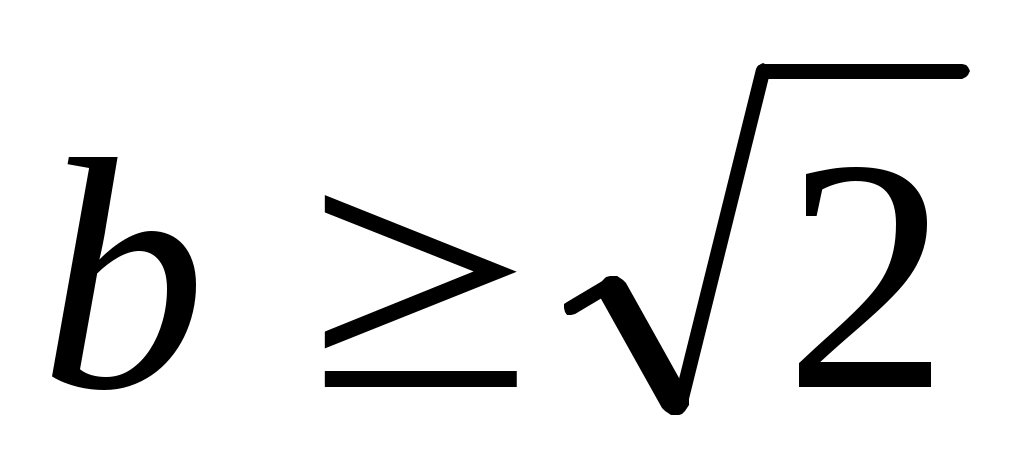 болғанда болғанда 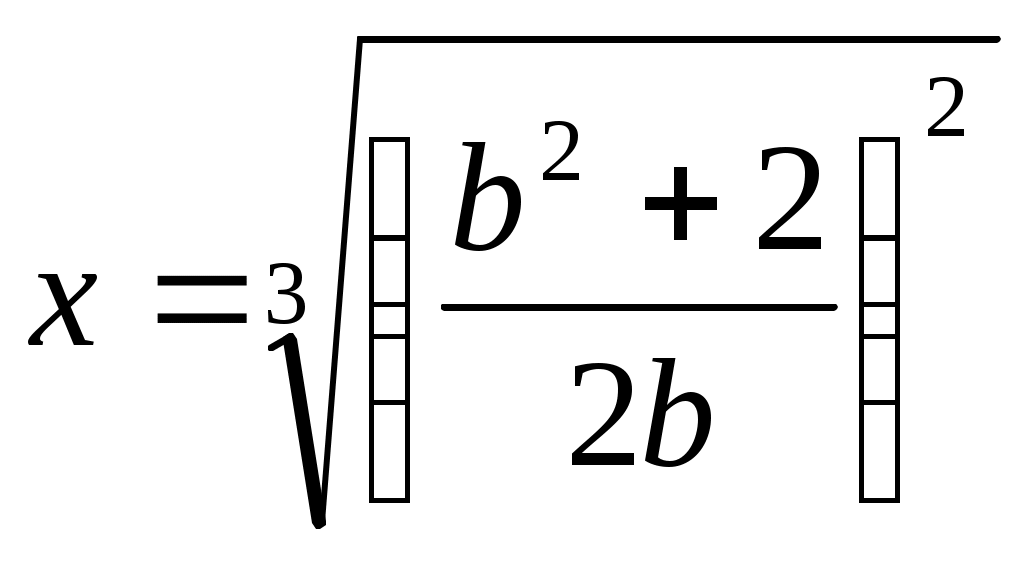 . .
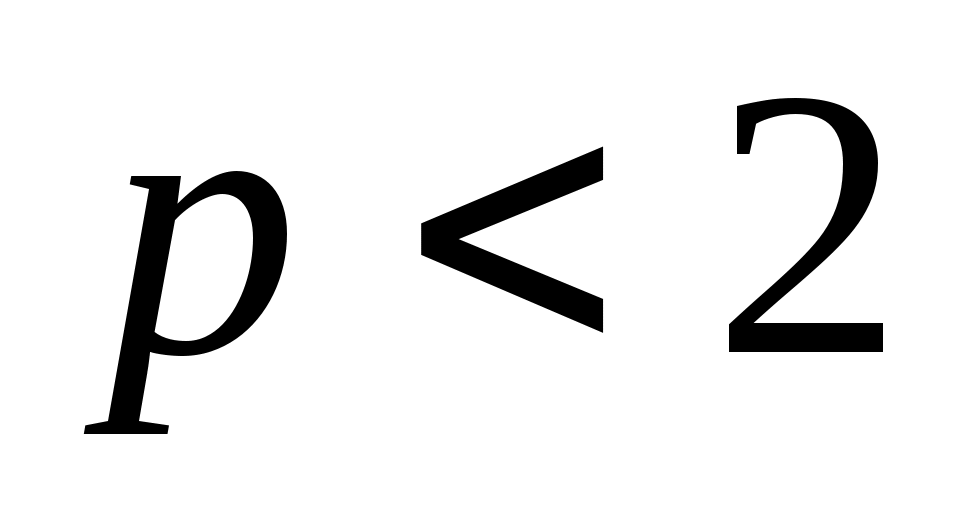 болғанда шешімі жоқ болғанда шешімі жоқ
Мысал 14. 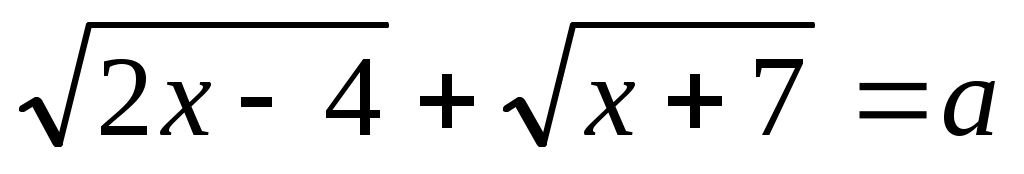 (1) (1)
Шешуі: 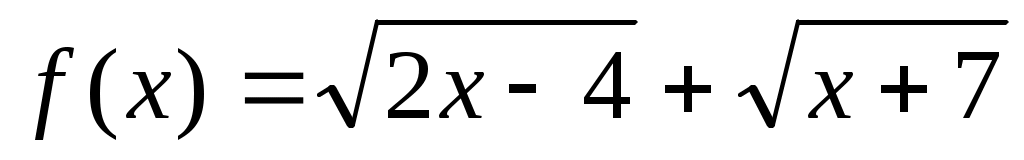 функциясы функциясы 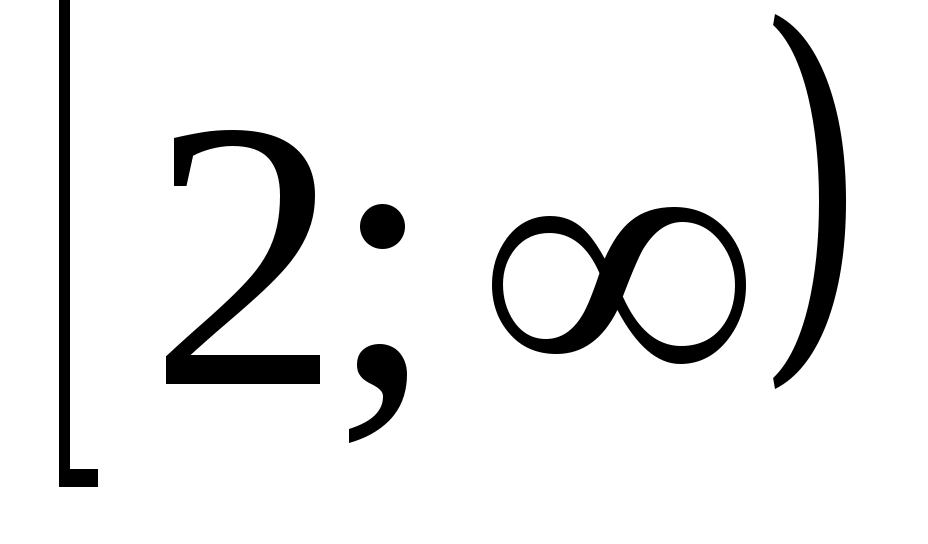 аралығында өседі және өзінің ең кіші мәнін х=2 нүктесінде қабылдайды. аралығында өседі және өзінің ең кіші мәнін х=2 нүктесінде қабылдайды. 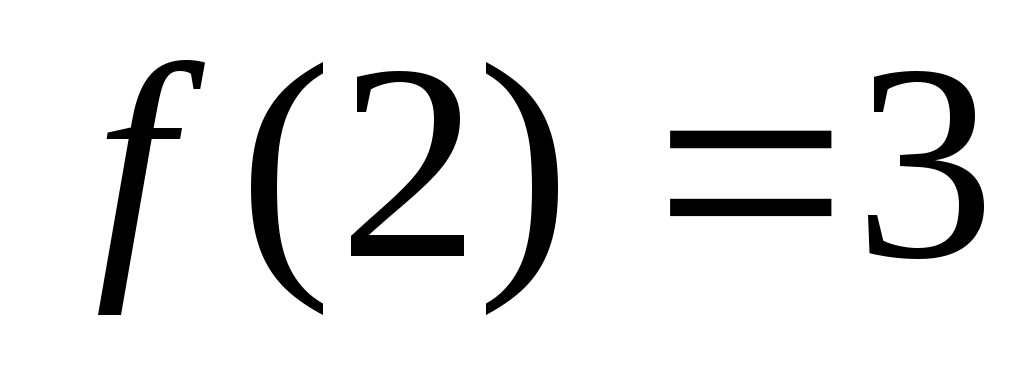 . Демек, . Демек, 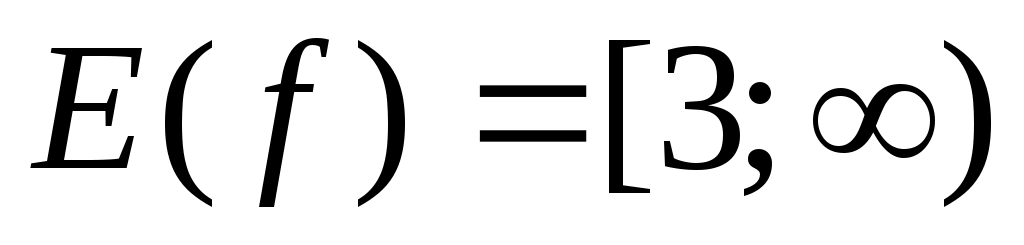 . Бұдан . Бұдан  параметрінің бақылау мәні 3 болатынын көреміз. параметрінің бақылау мәні 3 болатынын көреміз. 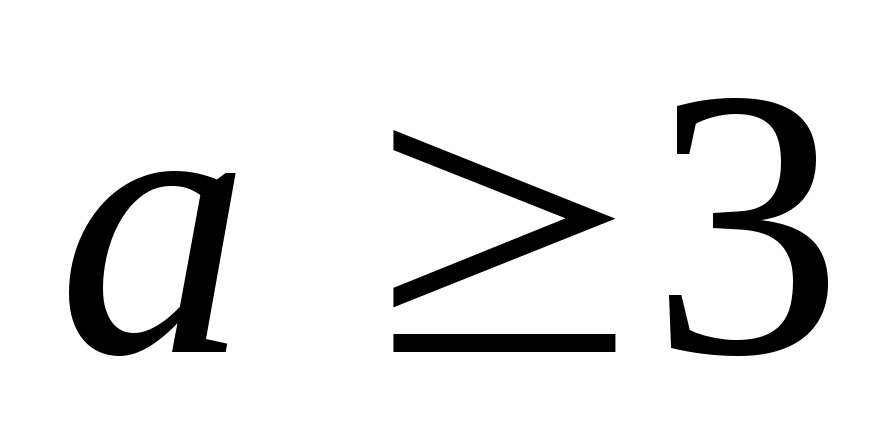 болғанда теңдеудің бір шешімі бар, ал болғанда теңдеудің бір шешімі бар, ал 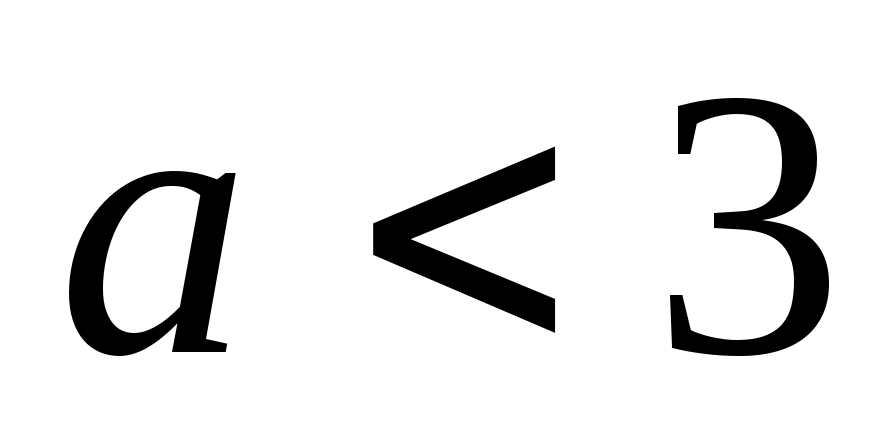
Болғанда теңдеудің шешімі болмайды. Яғни 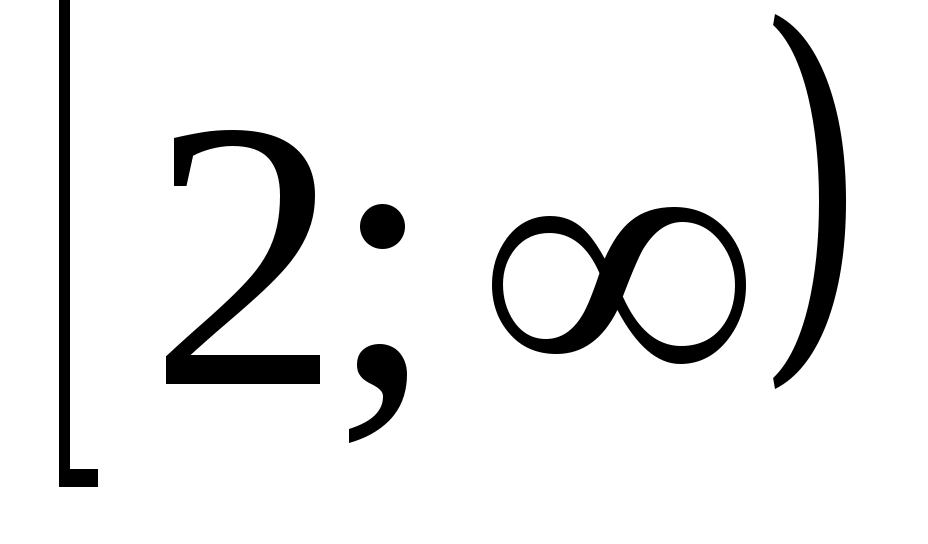 интервалында монотонды интервалында монотонды 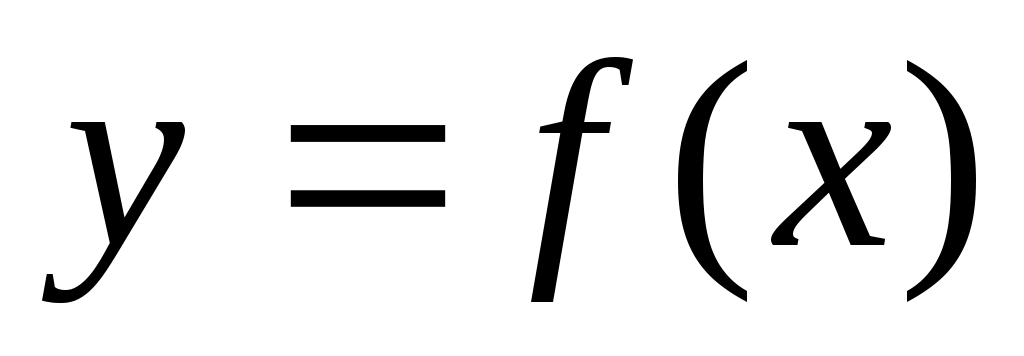 функциясының графигін функциясының графигін 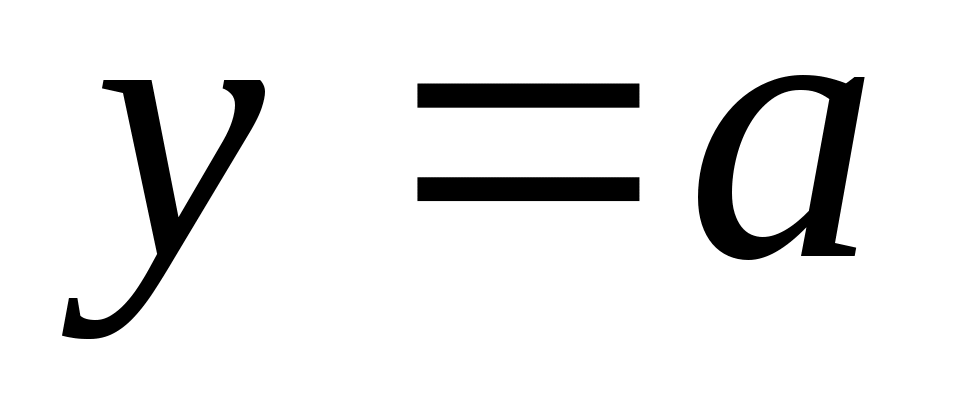 түзуі бір ғана нүктеде қияды немесе қимайды. түзуі бір ғана нүктеде қияды немесе қимайды.
Сонымен 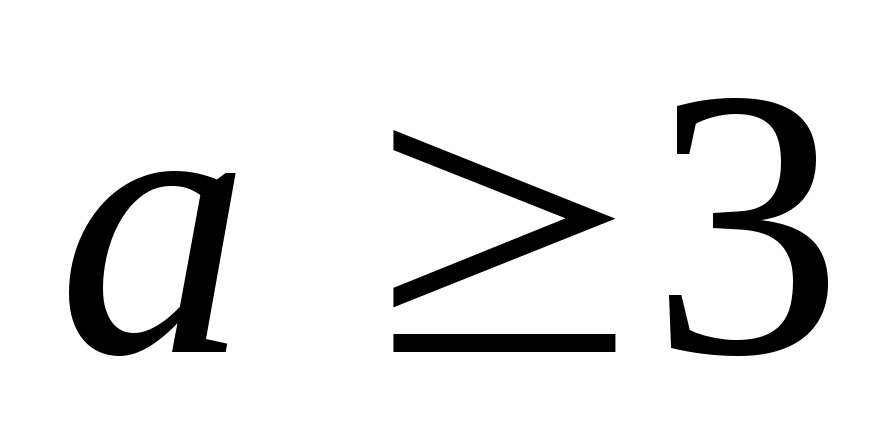 болсын. (1) теңдеуін болсын. (1) теңдеуін 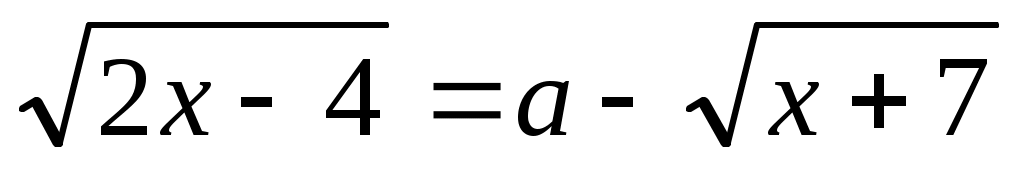 (2) түрінде жазып, екі бөлігін квадраттаймыз. Сонда (2) түрінде жазып, екі бөлігін квадраттаймыз. Сонда 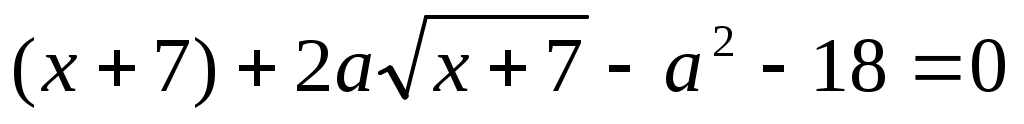 (3) (3)
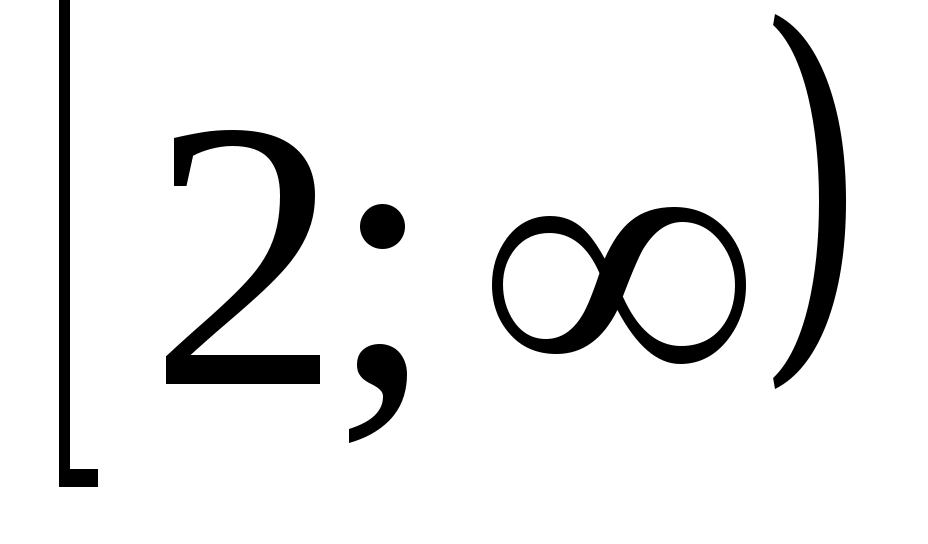 интервалында (1), (2), (3) теңдеулері мәндес. интервалында (1), (2), (3) теңдеулері мәндес. 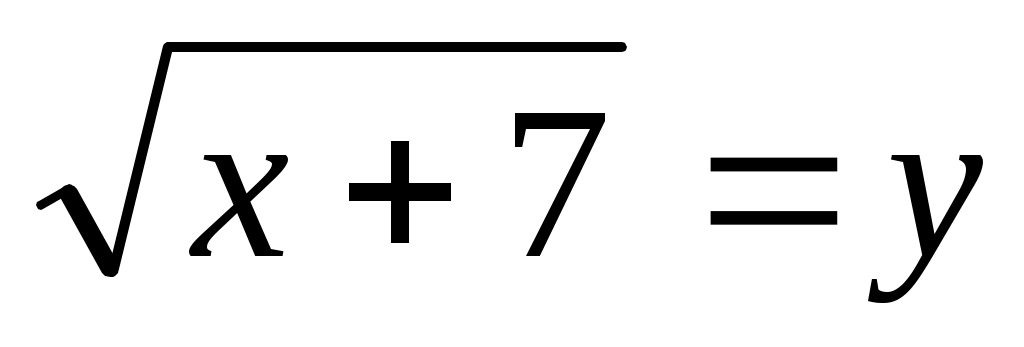 деп белгілейік, демек у≥0. Сонда (3) теңдеуі деп белгілейік, демек у≥0. Сонда (3) теңдеуі 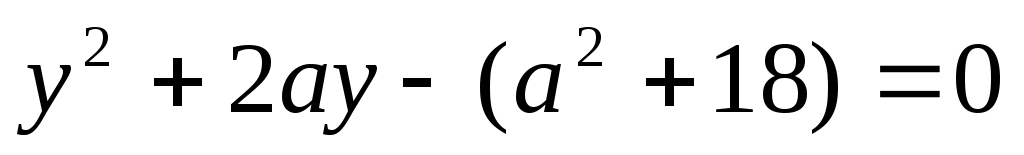 түріне келеді. Дискриминант түріне келеді. Дискриминант 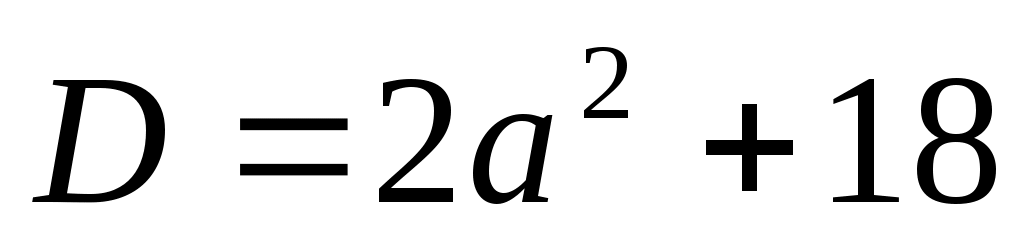 , ,  болғандықтан болғандықтан 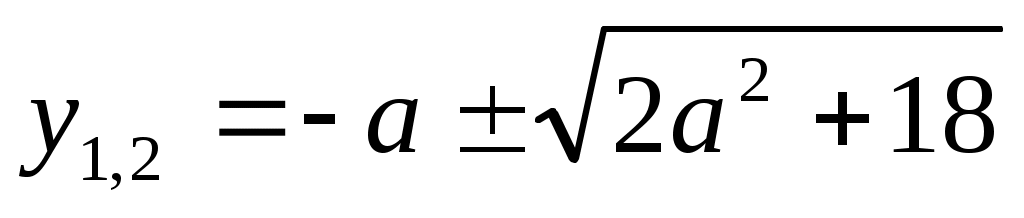 түбірін аламыз. у≥0 екенін ескерсек, түбірін аламыз. у≥0 екенін ескерсек, 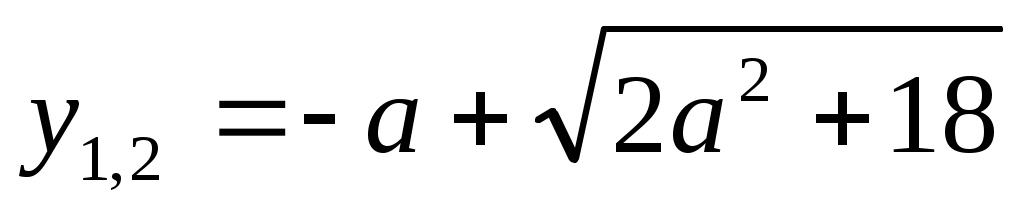 түбірі ғана жарамды. Осыдан түбірі ғана жарамды. Осыдан 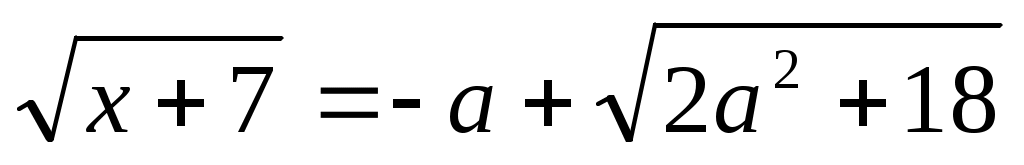 (4) теңдеуін аламыз. Теңдеудің екі бөлігі де оң сан болғандықтан квадраттай отырып, (4) теңдеуін аламыз. Теңдеудің екі бөлігі де оң сан болғандықтан квадраттай отырып, 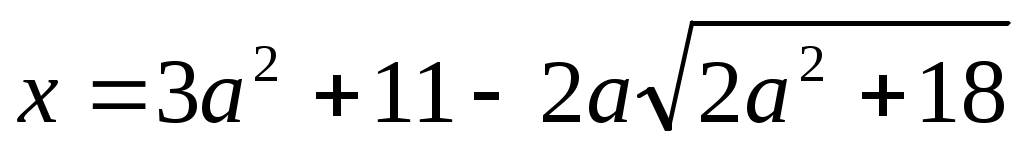 түбірін табамыз. Табылған түбір (1) теңдеуге де шешім болады. түбірін табамыз. Табылған түбір (1) теңдеуге де шешім болады.
Жауабы: 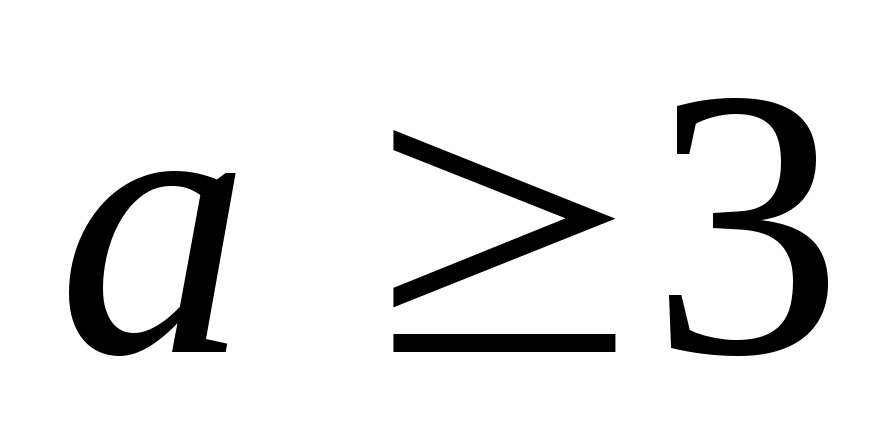 болғанда болғанда 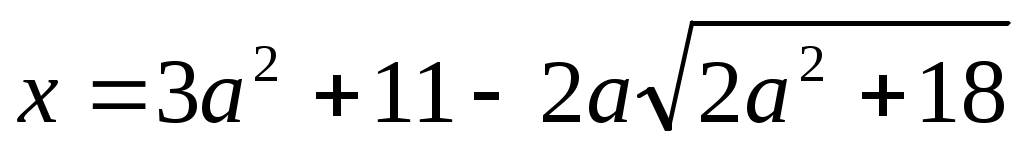
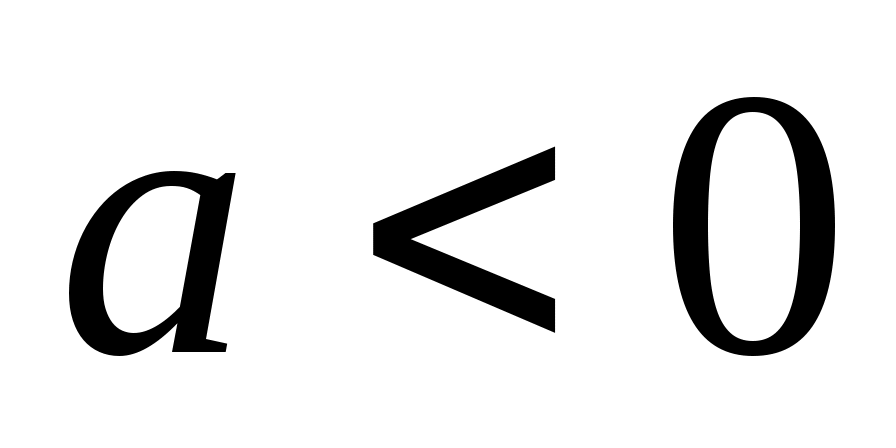 болғанда шешімі жоқ болғанда шешімі жоқ
Біз жоғарыда теңдеу шешудің кейбір әдістерін қарастырдық. Алайда, теңдеу шешудің тұрақты ережесі жоқ екенін ескерсек, кез келген есепті шығару үшін оқушының бойында жоғары теориялық даярлық мен ізденімпаздық, байқағыштық мен тапқырлық болуы қажет.
Пайдаланған әдебиеттер:
Ваховский Е.Б. и др. Задачи по элементарной математике. М. 1969
Галицкий М.А. и др. Углубленное изучение курса алгебры и математического анализа. М. 1990
Шарыгин И.Ф. Факультативный курс по математике. Решение задач. Учебное пособие для 10 класса средней школы. М. 1989.
Сканави М.И. и др. Сборник конкурсных задач по математике. М. 1978.
Шығыс Қазақстан облысы
Үржар ауданы
Тел: 7(72230)55551, 87773810150 |
|
|
 Скачать 389.5 Kb.
Скачать 389.5 Kb.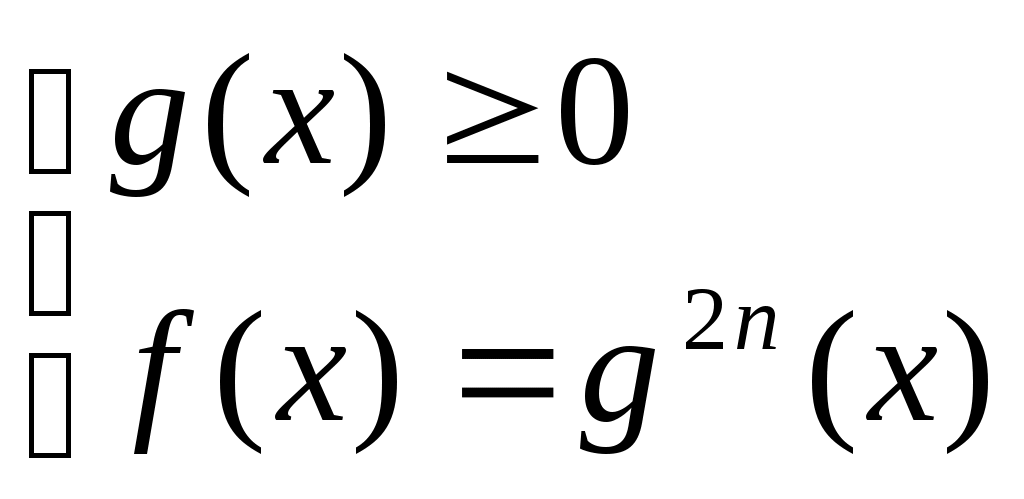
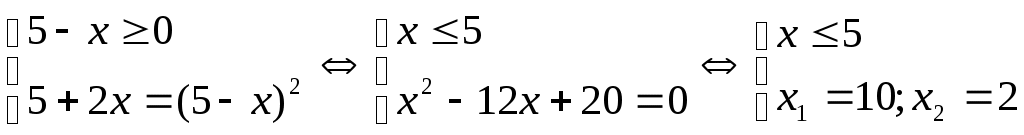
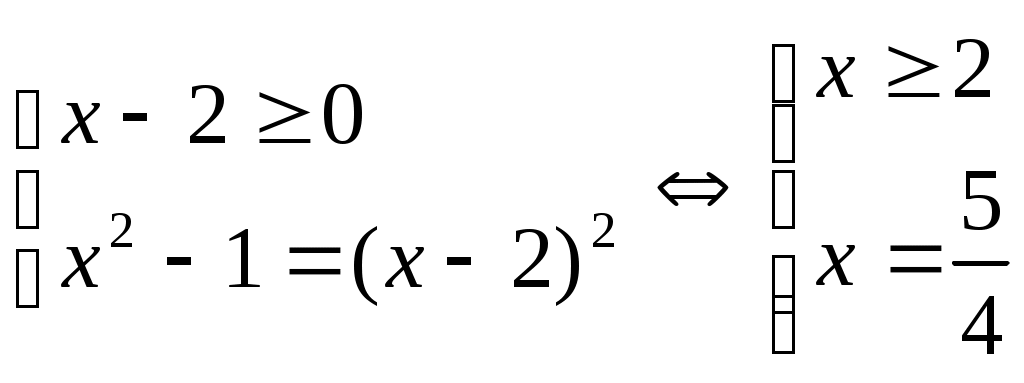 . Бұл жүйенің шешімі жоқ. Өйткені
. Бұл жүйенің шешімі жоқ. Өйткені 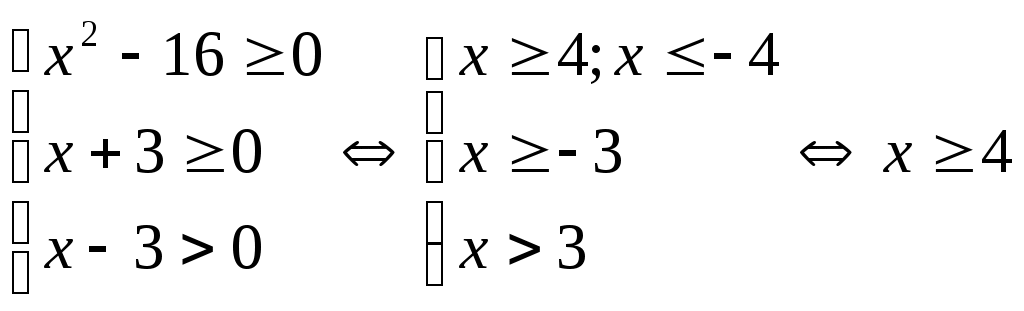 . Сонда ММО:
. Сонда ММО: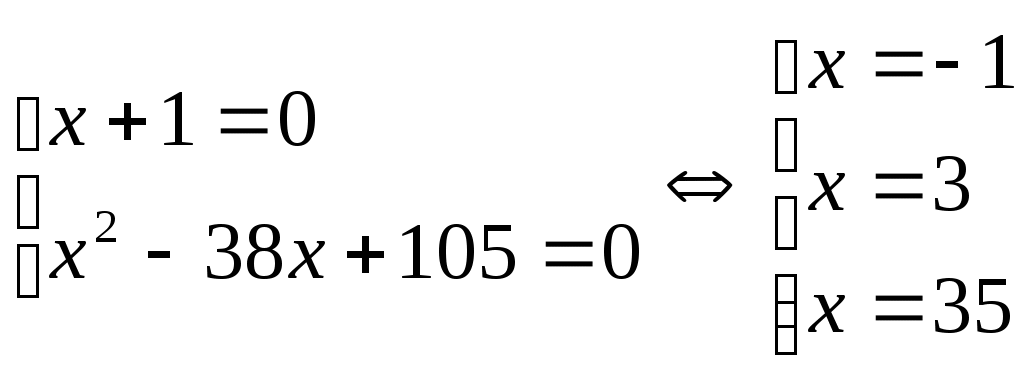 . Бұл табылған түбірлер МОО-на тиісті
. Бұл табылған түбірлер МОО-на тиісті 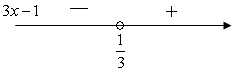
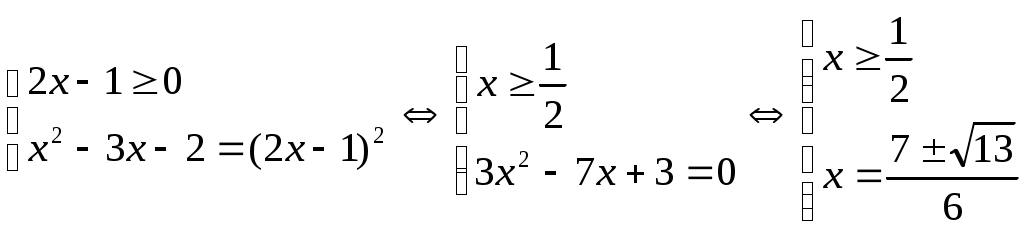 , бұдан
, бұдан 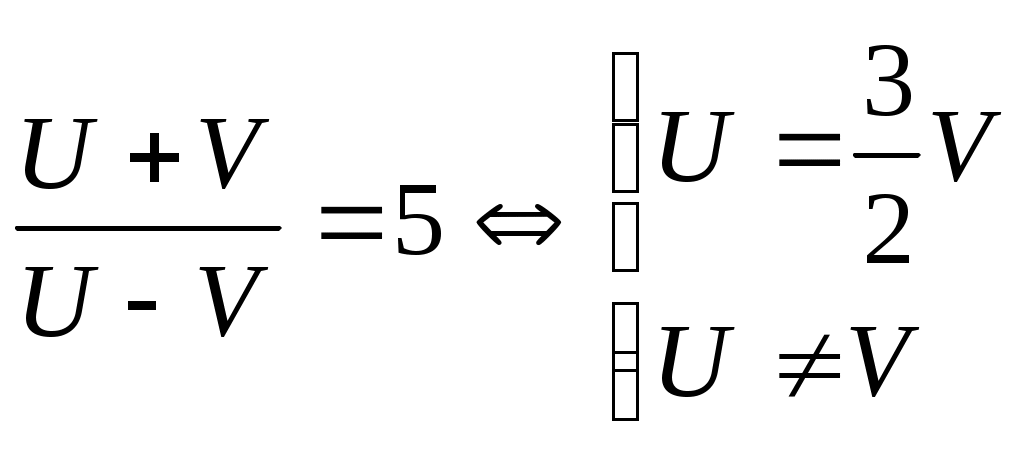 . Осы табылған мәнді (2) дегі орнына қойсақ,
. Осы табылған мәнді (2) дегі орнына қойсақ, 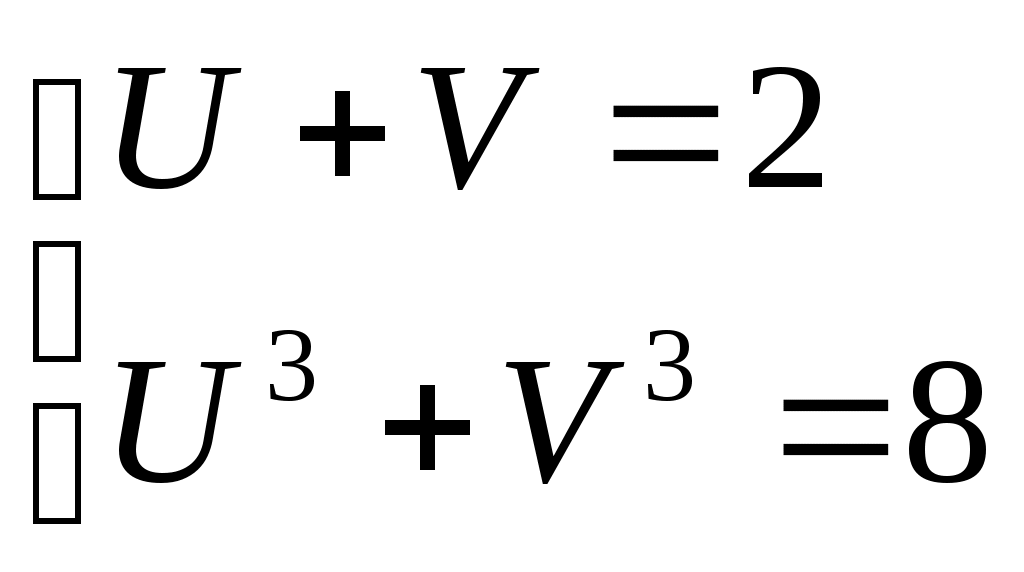 екі белгісізі бар жүйені шешеміз. Бұдан
екі белгісізі бар жүйені шешеміз. Бұдан 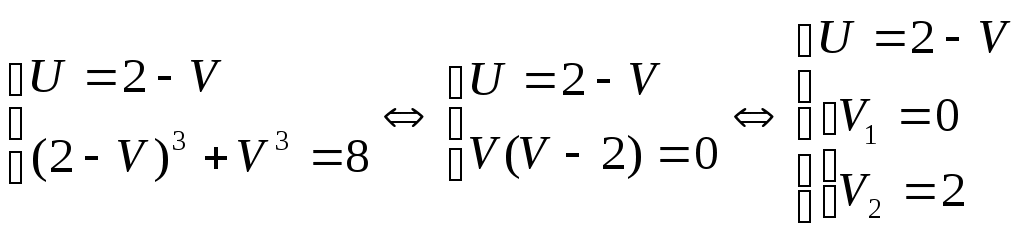 . Бұдан
. Бұдан 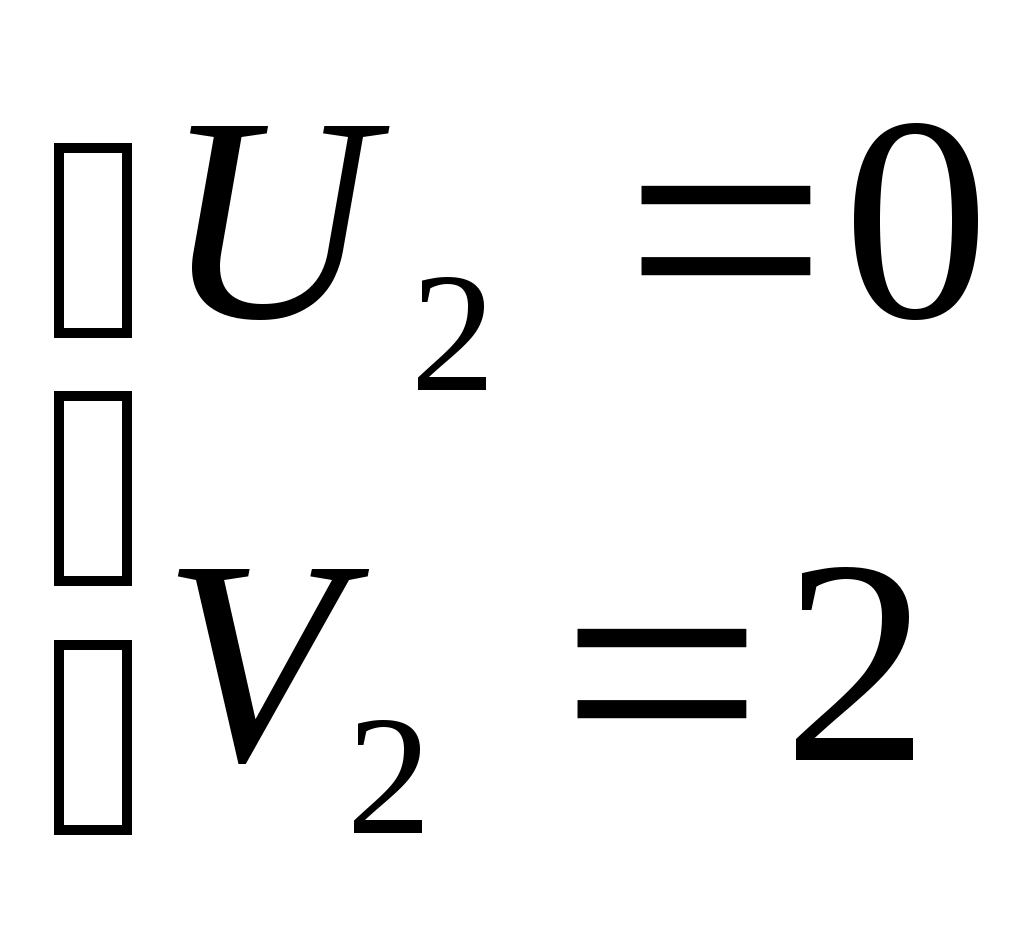 . Осылайша есеп келесі жүйелер жиынтығын шешуге келтіріледі:
. Осылайша есеп келесі жүйелер жиынтығын шешуге келтіріледі: 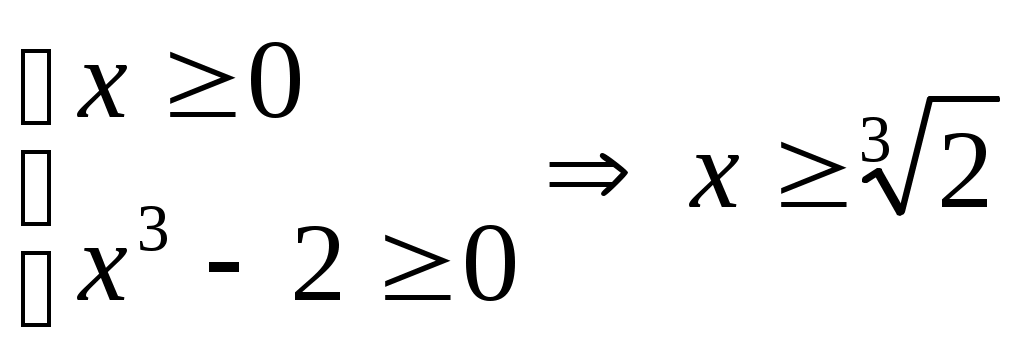 , яғни
, яғни