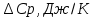Расчетно графическая работа физическая химия. РГР ФИЗ ХИМИЯ. Исследование 1 Для удобства последующих расчетов составляем таблицу исходных данных, используя справочный материал
 Скачать 112.81 Kb. Скачать 112.81 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное Учреждение высшего профессионального образования «Магнитогорский государственный технический университет им. Г.И. Носова» Кафедра физической химии и химической технологии РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА По курсу «Физическая химия» Раздел «Термодинамический анализ химических реакций» Вариант 1.5 Выполнила: Мухина В.В. Студент группы: МХб-20-1 (подпись) Проверил: (подпись) Магнитогорск 2021 Формулировка задания Исследование 1 Для удобства последующих расчетов составляем таблицу исходных данных, используя справочный материал. Таблица 1 Исходные данные для термодинамического расчета реакции Nb2O5(тв) + 3H2(газ) = 2NbO + 3H2O(газ)
1.1 . Расчет изменения изобарной теплоемкости ( 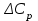 ) и теплового эффекта реакции ( ) и теплового эффекта реакции (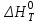 ) )Зависимость теплового эффекта реакции от температуры определяется законом Кирхгофа: 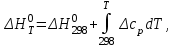 (1) (1) где: 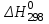 – стандартный тепловой эффект реакции при 298 К; – стандартный тепловой эффект реакции при 298 К;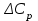 - изменение теплоёмкости системы в результате протекания реакции. - изменение теплоёмкости системы в результате протекания реакции. Последняя величина рассчитывается по уравнению: 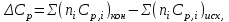 (2) (2)где 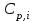 - мольная изобарная теплоёмкость i-го вещества, определяемая из уравнения: - мольная изобарная теплоёмкость i-го вещества, определяемая из уравнения: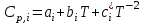 (3) (3)Рассчитаем 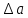 : : 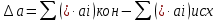 ; ;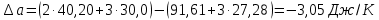 Рассчитаем Рассчитаем 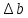 : :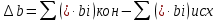 ; ;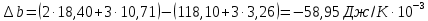 Рассчитаем 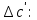 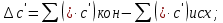 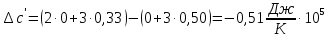 Найдем 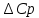 : :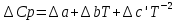 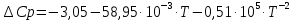 Температурный интервал 1750-2000 Температурный интервал 1750-2000 с шагом: 50 При Т=1750: 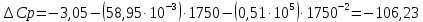 Остальные Остальные 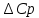 при различных температурах рассчитывается аналогично. при различных температурах рассчитывается аналогично.Рассчитаем значения 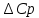 при различных температурах и сведем эти значения в табл.2. при различных температурах и сведем эти значения в табл.2.Таблица 2
Зависимость изменения изобарной теплоемкости от температуры для реакции Nb2O5(тв) + 3H2(газ) = 2NbO + 3H2O(газ) По данным табл.2. построить зависимость 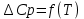 . .  Рис.1. Зависимость изменения изобарной теплоемкости от температуры для реакции Nb2O5(тв) + 3H2(газ) = 2NbO + 3H2O(газ) Значение Н298 в уравнении (1) определяется по стандартным теплотам образования Н298, i Н298 = (ni Н298, i )кон - (ni Н298, i)исх. (4) В рассматриваемом случае уравнение (4) имеет вид: 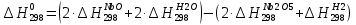 (5) (5)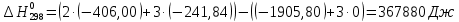 В соответствии с заданием необходимо рассчитать тепловые эффекты в интервале температур 1750-2000К при шаге температуры 50К. Получим уравнение зависимости теплового эффекта реакции от температуры: В соответствии с заданием необходимо рассчитать тепловые эффекты в интервале температур 1750-2000К при шаге температуры 50К. Получим уравнение зависимости теплового эффекта реакции от температуры: 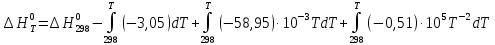 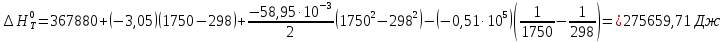 Остальные значения 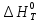 при различных температурах T=1750-2000 рассчитываются аналогично. при различных температурах T=1750-2000 рассчитываются аналогично.Таблица 3 Величина 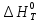 при различных температурах для реакции при различных температурах для реакцииNb2O5(тв) + 3H2(газ) = 2NbO + 3H2O(газ)
Зависимость 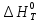 =f(T), построенная по данным табл.3 представлена на рис.2. =f(T), построенная по данным табл.3 представлена на рис.2. 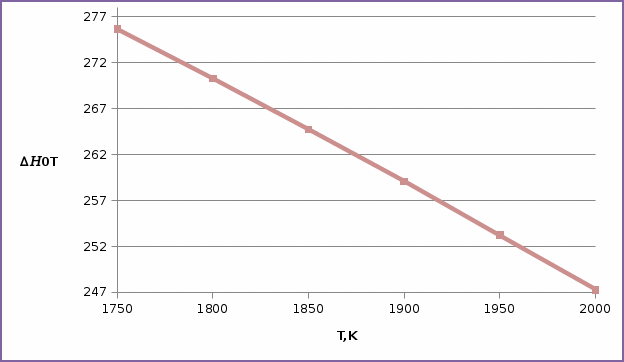 Рис.2. Зависимость теплового эффекта от температуры для реакции Nb2O5(тв) + 3H2(газ) = 2NbO + 3H2O(газ) 1.2Расчёт изменения энтропии реакции Изменение энтропии системы в результате протекания процесса определяется по уравнению: 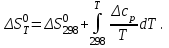 (6) (6)В этом уравнении 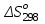 – стандартное изменение энтропии для реакции при 298К, определяемое по мольным стандартным энтропиям веществ – стандартное изменение энтропии для реакции при 298К, определяемое по мольным стандартным энтропиям веществ 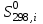 : :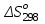 = (ni = (ni 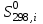 )кон - (ni )кон - (ni 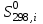 )исх (7) )исх (7)Значения 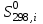 для соответствующих веществ приведены в табл. 1, после их подстановки в уравнение (7) получим: для соответствующих веществ приведены в табл. 1, после их подстановки в уравнение (7) получим: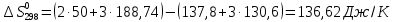 Выведем расчетное уравнение изменения энтропии от температуры: 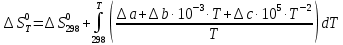 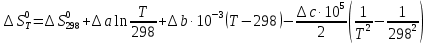 , (8) , (8)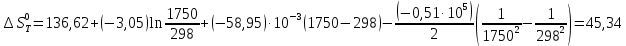  Остальные значения Остальные значения 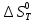 при различных температурах T=1750-2000 рассчитываются аналогично. при различных температурах T=1750-2000 рассчитываются аналогично.Таблица 4 Значения изменения энтропии ( 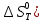 при различных температурах для реакции при различных температурах для реакцииNb2O5(тв) + 3H2(газ) = 2NbO + 3H2O(газ)
По данным табл.4 построим график 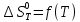 . .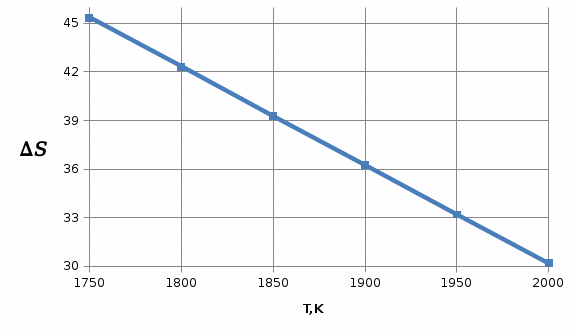 Рис.3. Зависимость изменения энтропии от температуры для реакции  1.3. Расчет изменения стандартной энергии Гиббса При расчете изменения стандартной энергии Гиббса для реакции воспользуемся уравнением Гиббса-Гельмгольца. 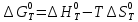 , (9) , (9) Найденные величины изменения стандартной энергии Гиббса приведены в табл.5, по данным которой построена зависимость  , изображенная на рис.4. , изображенная на рис.4. 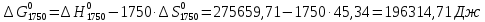 Остальные значения Остальные значения 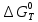 при различных температурах T=1750-2000 рассчитываются аналогично. при различных температурах T=1750-2000 рассчитываются аналогично.Таблица 5 Значения изменения стандартной энергии Гиббса ( 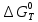 ) при различных температурах для реакции ) при различных температурах для реакцииNb2O5(тв) + 3H2(газ) = 2NbO + 3H2O(газ)
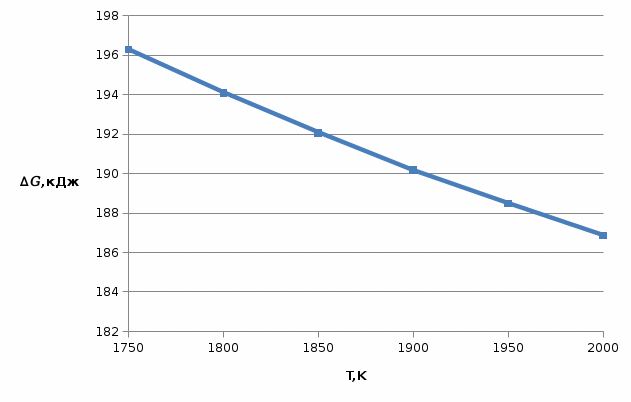 Рис.4. Зависимость изменения стандартной энергии Гиббса от температуры для реакции Nb2O5(тв) + 3H2(газ) = 2NbO + 3H2O(газ) 1.4. Вывод уравнения зависимости константы равновесия от температуры Константа равновесия связана с изменением стандартной энергии Гиббса соотношением: 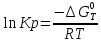 (10) (10)После подстановки выражения (13) в уравнение (14) получим: 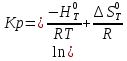 (11) (11)Можно полагать, что в сравнительно небольшом интервале температур тепловой эффект реакции ( 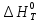 ) и изменение энтропии ( ) и изменение энтропии (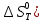 практически постоянные величины (это подтверждают и результаты табл.3 и 4). Отсюда уравнение можно записать в виде: практически постоянные величины (это подтверждают и результаты табл.3 и 4). Отсюда уравнение можно записать в виде: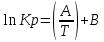 (12) , (12) , где A и B-постоянные, которые соответственно равны: 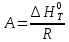 (13) (13)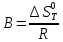 (14) (14) Уравнение (12) отвечает линейной зависимости 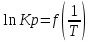 . . Определим коэффициенты A и B графически. С этой целью по уравнению (10) и данным табл.5 рассчитаем величину 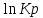 в заданном интервале температур. в заданном интервале температур. 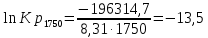 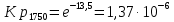 Таблица 6 Константы равновесия для реакции Nb2O5(тв) + 3H2(газ) = 2NbO + 3H2O(газ) при различных температурах
Для графического определения констант A и B в уравнении (12) по данным таблицы 6 построим зависимость 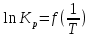 . . 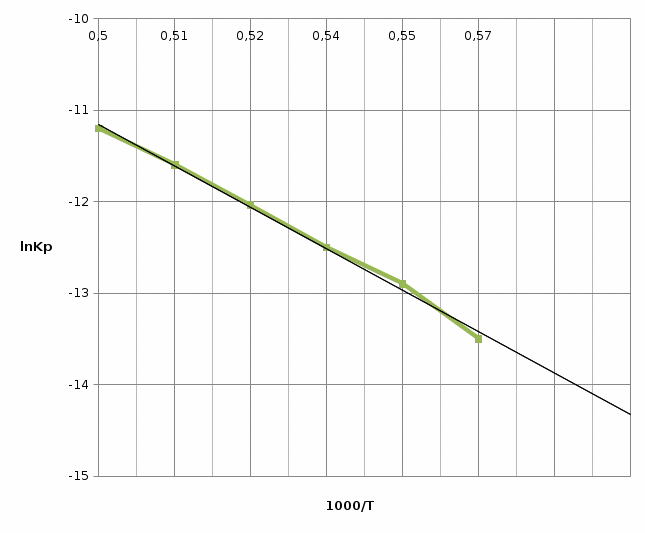 Рис.5. Зависимость lnKp от обратной температуры для реакции Рис.5. Зависимость lnKp от обратной температуры для реакцииNb2O5(тв) + 3H2(газ) = 2NbO + 3H2O(газ) Рассчитаем коэффициент A 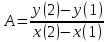 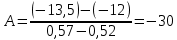 По значению коэффициента A рассчитаем величину среднего теплового эффекта 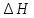 : : 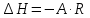 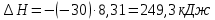 Рассчитаем коэффициент B 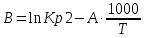 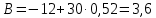 По значению коэффициента B рассчитаем величину изменения энтропии 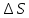 : :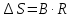 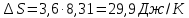 Полученные данные отлично согласуются с данными, приведенными в табл.2 и 3. Исследование 2. 2.1 Определение количества фаз, независимых компонентов и степени свободы. Рассматриваемая система состоит из трех фаз: двух твердых фаз Nb2O5 и NbO, а также газообразной, представляющей смесь газов H2 и H2O. Таким образом, ф=3. Число независимых компонентов k равно наименьшему числу веществ, необходимых для выражения состава всех фаз системы. Это число определяют как общее число веществ в системе m за вычетом числа связей между ними r. Связь между веществами, входящими в рассматриваемую систему, выражается уравнением реакции. Следовательно: 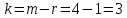 (15) (15)Число степеней свободы c равно числу независимых переменных системы (давление, температуры, концентрации компонентов), которые можно изменить в некоторых пределах так, чтобы число и природа фаз оставались прежними. По правилу фаз Гиббса: 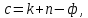 (16) (16) Где n- число внешних параметров, влияющих на состояние равновесия системы. В нашем случае n=1 (только температура, так как в нашем уравнении давление не влияет на состояние равновесия). Для рассматриваемой системы: 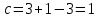 Вывод: c=1 это означает, что не нарушая состояния равновесия в известных пределах можно изменить 1 параметр, при этом число природы фаз не изменится. 2.2. Определение возможного направления. Изотерма Вант-Гоффа 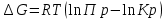 Pобщ=202,6 кПа 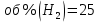 Т=1700 К 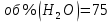 ПP- произведение фактического парциального давления газообразных компонентов Кр- константа равновесия 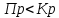 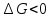 равновесие смещается в сторону продуктов реакции равновесие смещается в сторону продуктов реакции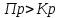 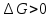 равновесие смещается в сторону исходных веществ равновесие смещается в сторону исходных веществРассчитаем Кр при заданной Т 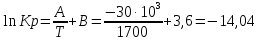 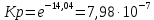 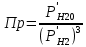  P’H2O, P’H2 – фактические Пр, выраженные в относительных единицах. P’H2O, P’H2 – фактические Пр, выраженные в относительных единицах.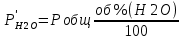 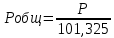 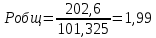 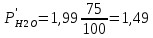 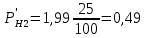 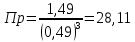  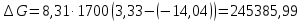 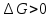 следовательно, равновесие смещается в сторону исходных веществ. следовательно, равновесие смещается в сторону исходных веществ.2.3. Определение равновесного состояния состава газовой смеси Nb2O5(тв) + 3H2(газ) = 2NbO + 3H2O(газ) Обозначим через x мольную долю H2 , тогда мольная доля H2O будет 1-x Запишем Kp для данной реакции при заданной T 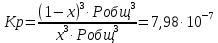  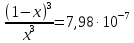 x1=0,99 x1=0,99x2=1,0045 x3=1,004 Физический смысл имеет только первый корень, т.к. мольная доля не может быть отрицательной и больше единицы. Таким образом, в равновесной газовой смеси мольная доля водорода NH2=0,99 и мольная доля воды NH2O=1-0,99=0,01. Содержание этих газов, выраженное в объемных процентах (Об.%) составит: 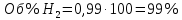 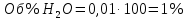 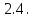 Установление направления смещения равновесия. Установление направления смещения равновесия.Принцип Ле Шателье 1) При увеличении T равновесие смещается в сторону эндотермической реакции Так как 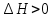 реакция эндотермическая.Следовательно, равновесие смещается в сторону продуктов реакции(вправо). реакция эндотермическая.Следовательно, равновесие смещается в сторону продуктов реакции(вправо).2) При увеличении P равновесие смещается в сторону веществ с меньшим объемом газовой фазы. В нашем случае давление не влияет на состояние равновесия. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||