лр работа. ЛР2_РЭРС. Исследование амплитудного спектра радиоимпульса с помощью программы spectr получили график прямоугольного импульса длительностью 1 c и его амплитудного спектра
 Скачать 3.78 Mb. Скачать 3.78 Mb.
|
|
1. Исследование амплитудного спектра радиоимпульса 1.1. С помощью программы SPECTR получили график прямоугольного импульса длительностью  = 1 c и его амплитудного спектра. = 1 c и его амплитудного спектра. Рисунок 1.1. График прямоугольного импульса длительностью  =1 =1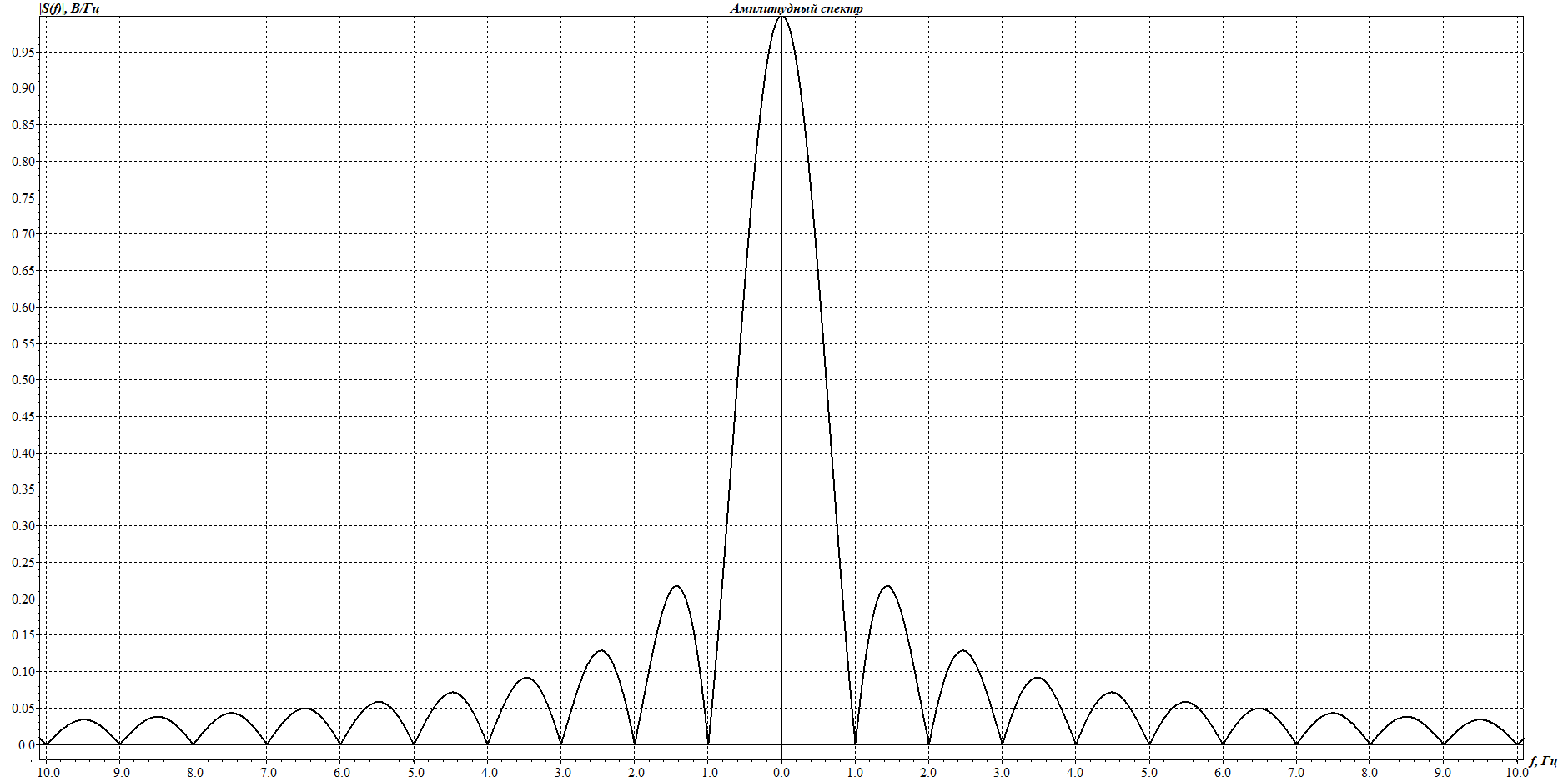 Рисунок 1.2 График амплитудного спектра прямоугольного импульса длительностью  =1 =11.2. Получили графики прямоугольного радиоимпульса с несущей частотой 𝑓0= 1 кГц и его амплитудного спектра.  Рисунок 1.3 график прямоугольного радиоимпульса с несущей частотой 𝑓0= 1 кГц  Рисунок 1.4 график амплитудного спектра прямоугольного радиоимпульса с несущей частотой 𝑓0= 1 кГц 1.3 F0=2000  Рисунок 1.5 график прямоугольного радиоимпульса с несущей частотой 𝑓0= 2 кГц 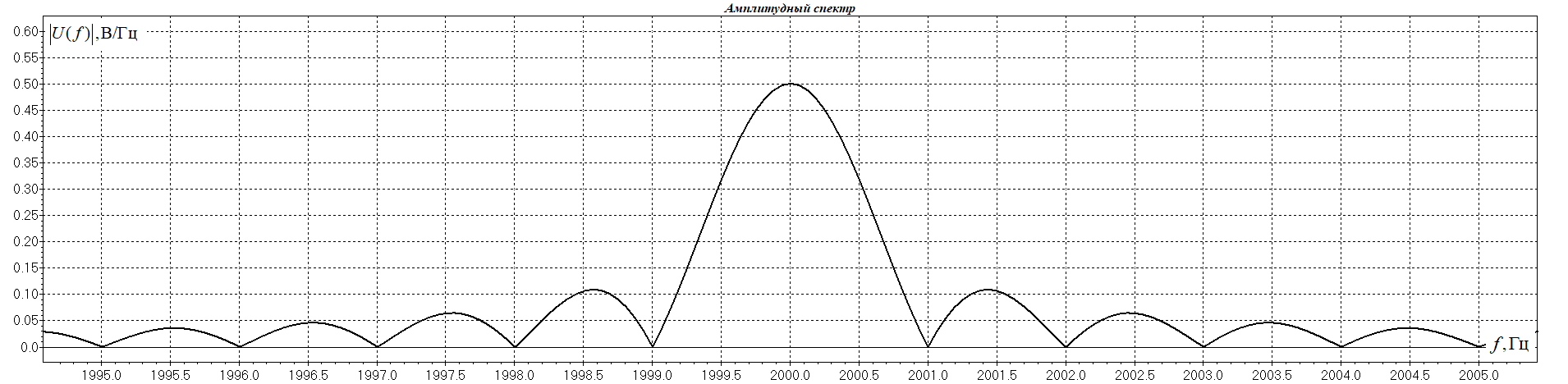 Рисунок 1.6 график амплитудного спектра прямоугольного радиоимпульса с несущей частотой 𝑓0= 2 кГц F=5000  Рисунок 1.6 график прямоугольного радиоимпульса с несущей частотой 𝑓0= 5 кГц  Рисунок 1.7 график амплитудного спектра прямоугольного радиоимпульса с несущей частотой 𝑓0= 5 кГц 1.4. Для любой из указанных выше частот (𝑓0= 2 кГц) получили графики прямоугольного радиоимпульса и его амплитудного спектра для  = 2 с и = 2 с и  = 5 с. = 5 с.Рисунок 1.8 график прямоугольного радиоимпульса 𝑓0= 2 кГц  = 2 с = 2 с  Рисунок 1.9 график амплитудного спектра прямоугольного радиоимпульса 𝑓0= 2 кГц  =2 с =2 с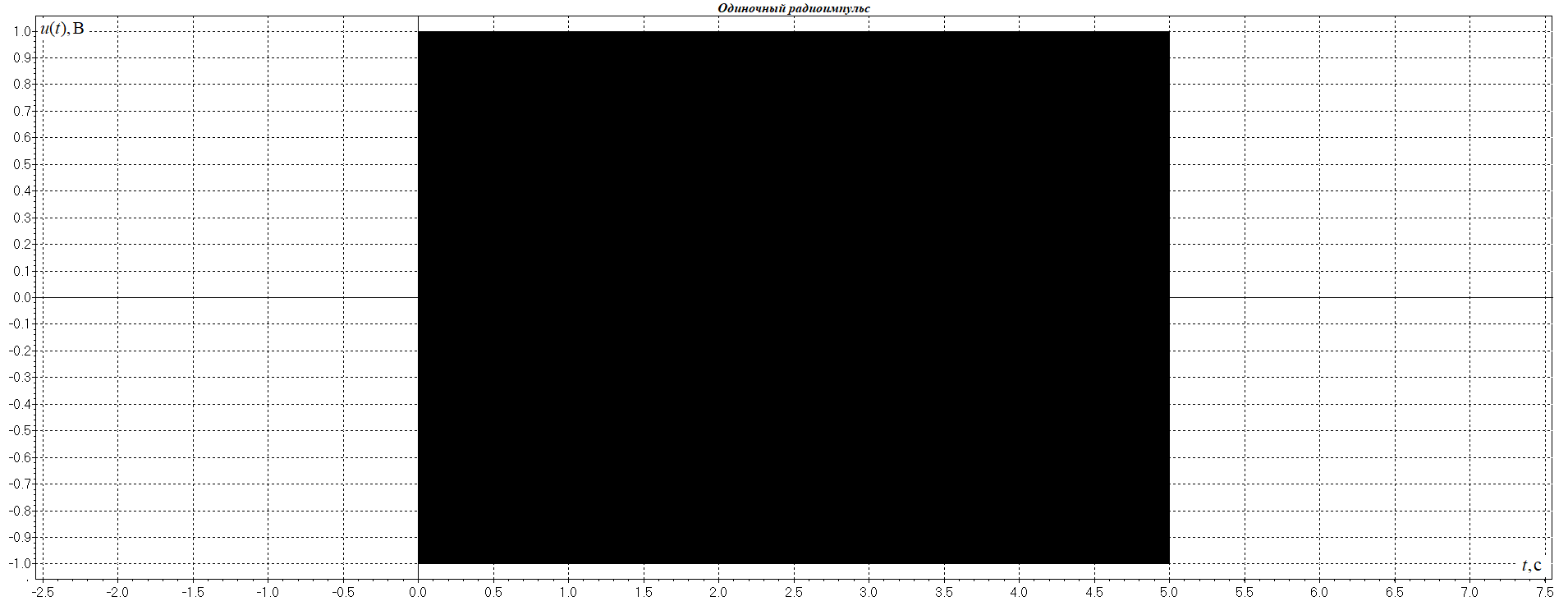 Рисунок 1.10 график прямоугольного радиоимпульса 𝑓0= 2 кГц  = 5 с = 5 с Рисунок 1.11 график амплитудного спектра прямоугольного радиоимпульса 𝑓0= 2 кГц  = 5 с = 5 с1.5. Вывод: наибольшая по амплитуде гармоника (нулевая) находится на несущей частоте. Длительность радиосигнала влияет на его амплитуду и ширину амплитудного спектра: чем больше длительность, тем больше амплитуда и тем уже ширина спектра. 2. Исследование спектра периодической последовательности радиоимпульсов 2.1. С помощью программы SPECTR получили временную и спектральную диаграммы для периодической последовательности прямоугольных видеоимпульсов длительностью и  = 1 с со скважностью Q = 5. = 1 с со скважностью Q = 5. Рисунок 2.1 временная диаграмма периодической последовательности прямоугольных видеоимпульсов  = 1 с. и Q= 5 = 1 с. и Q= 5 Рисунок 2.2 график амплитудного спектра прямоугольного видеоимпульса  =1 с. и Q = 5 =1 с. и Q = 5 Рисунок 2.3 график фазового спектра прямоугольного видеоимпульса  =1 с. и Q = 5 =1 с. и Q = 52.2. Получили аналогичные диаграммы для периодической последовательности прямоугольных радиоимпульсов с несущей частотой 𝑓0 =1 кГц  Рисунок 2.3 временная диаграмма периодической последовательности прямоугольных радиоимпульсов 𝑓0 =1 кГц  = 1 с. и Q = 5 = 1 с. и Q = 5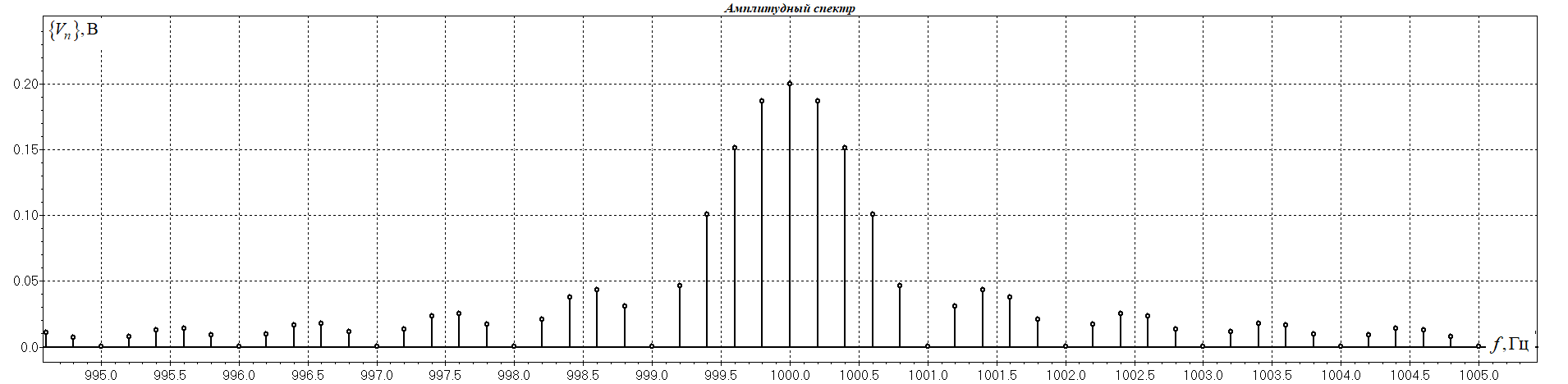 Рисунок 2.4 график амплитудного спектра прямоугольного радиоимпульса f0=1 кГц  =1 с. и Q = 5 =1 с. и Q = 5 Рисунок 2.5 график фазового спектра прямоугольного радиоимпульса f0=1 кГц  =1 с. и Q = 5 =1 с. и Q = 52.3 F=2000  Рисунок 2.6 временная диаграмма периодической последовательности прямоугольных радиоимпульсов 𝑓0= 2 кГц  = 1с. и Q = 5 = 1с. и Q = 5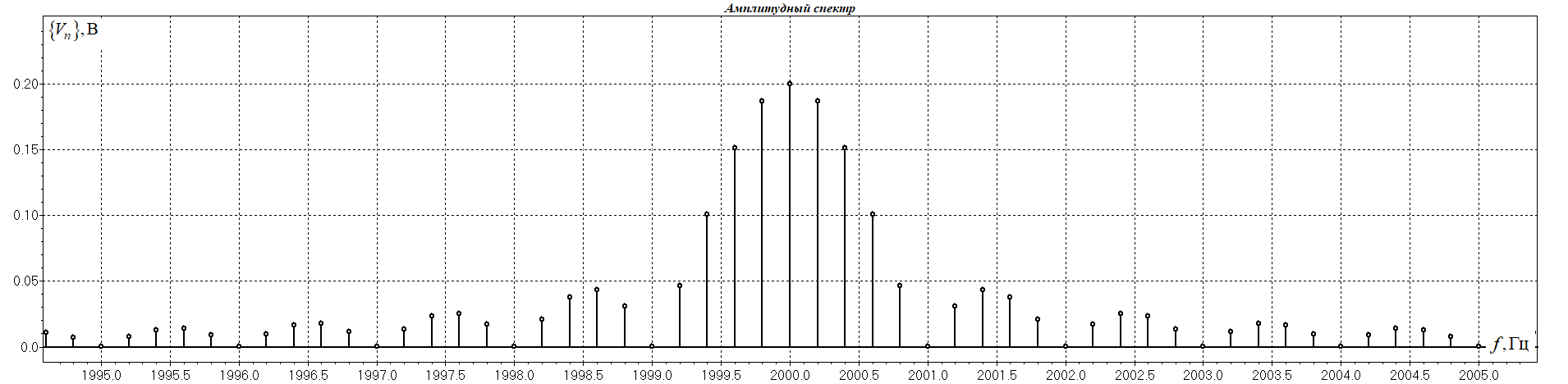 Рисунок 2.7 график амплитудного спектра прямоугольного радиоимпульса f0=2 кГц  =1 с. и Q = 5 =1 с. и Q = 5 Рисунок 2.8 график фазового спектра прямоугольного радиоимпульса f0=2 кГц  =1 с. и Q = 5 =1 с. и Q = 5F=5000  Рисунок 2.9 временная диаграмма периодической последовательности прямоугольных радиоимпульсов 𝑓0 =5 кГц  = 1 с. и Q = 5 = 1 с. и Q = 5 Рисунок 2.10 график амплитудного спектра прямоугольного радиоимпульса f0=5 кГц  =1 с. и Q = 5 =1 с. и Q = 5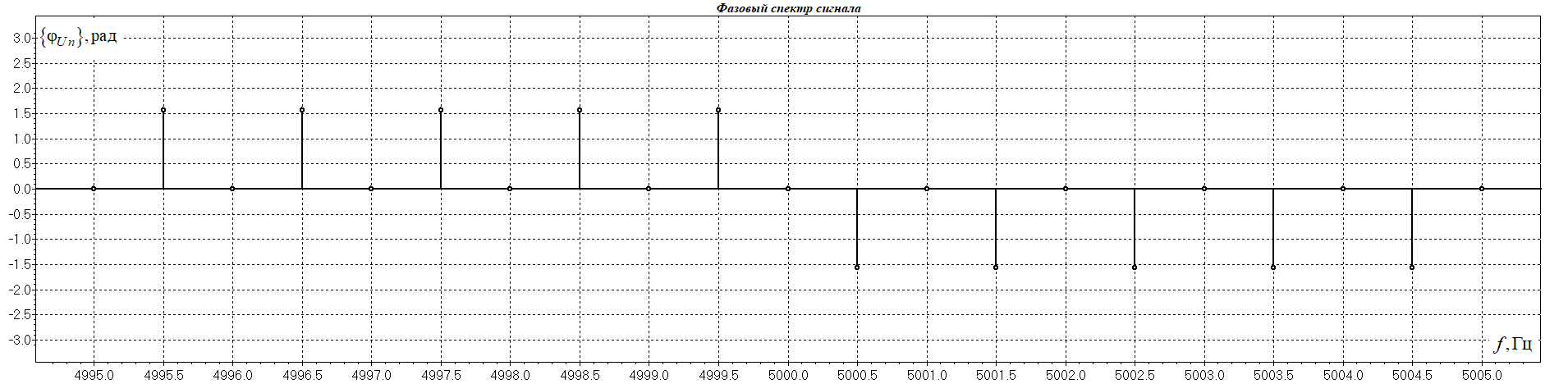 Рисунок 2.11 график фазового спектра прямоугольного радиоимпульса f0=5 кГц  =1 с. и Q = 5 =1 с. и Q = 52.4 Вывод: форма видеосигналов на временной диаграмме аналогична форме, огибающей радиоимпульсов, с той лишь разницей, что в случае радиоимпульса участок с амплитудой в 1 В закрашивается чёрным цветом, так как там происходит большое количество колебаний, а не одно. 3. Исследование спектра экспоненциального радиоимпульса Повторили п.1 для экспоненциального импульса с параметром t0,01 =1 с, задавая значения 𝑓0 = 2; 5; 10 кГц.  Рисунок 3.1 график экспоненциального радиоимпульса t0,01 = 1 с 𝑓0 = 2 кГц  Рисунок 3.2 график амплитудного спектра экспоненциального радиоимпульса t0,01 = 1 с 𝑓0 =2 кГц 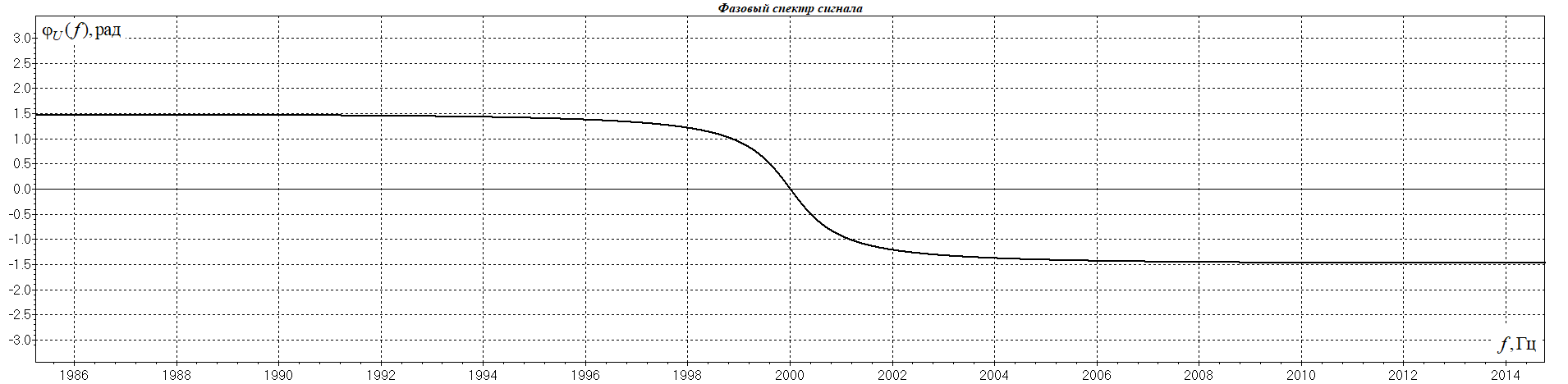 Рисунок 3.3 график фазового спектра экспоненциального радиоимпульса t0,01 = 1 с 𝑓0 = 2 кГц 3.2 f-5000  Рисунок 3.4 график экспоненциального радиоимпульса t0,01 = 1 с 𝑓0 = 5 кГц  Рисунок 3.5 график амплитудного спектра экспоненциального радиоимпульса t0,01 = 1 с 𝑓0 =5 кГц  Рисунок 3.3 график фазового спектра экспоненциального радиоимпульса t0,01 = 1 с 𝑓0 = 5 кГц 3.3 f-10000  Рисунок 3.9 график экспоненциального радиоимпульса t0,01 = 1 с 𝑓0 = 10 кГц  Рисунок 3.5 график амплитудного спектра экспоненциального радиоимпульса t0,01 = 1 с 𝑓0 =10 кГц  Рисунок 3.3 график фазового спектра экспоненциального радиоимпульса t0,01 = 1 с 𝑓0 = 10 кГц 4. Исследование спектра периодической последовательности экспоненциальных радиоимпульсов. Повторить п.2 для экспоненциального импульса с параметром t0,01 =1 с, задавая значения 𝑓0= 2; 5; 10 кГц. 4.1 f-2000  Рисунок 4.1 временная диаграмма периодической последовательности экспоненциальных радиоимпульсов t0,01 = 1 с. Q = 5 𝑓0 = 2 кГц  Рисунок 4.2 спектральная диаграмма периодической последовательности экспоненциальных радиоимпульсов t0,01 = 1 с. Q= 5 𝑓0 = 2 кГц  Рисунок 4.3 временная диаграмма фазового спектра экспоненциальных радиоимпульсов t0,01 = 1 с. Q= 5 𝑓0 = 2 кГц 4.2 f-5000  Рисунок 4.4 временная диаграмма периодической последовательности экспоненциальных радиоимпульсов t0,01 = 1 с. Q = 5 𝑓0 = 5 кГц 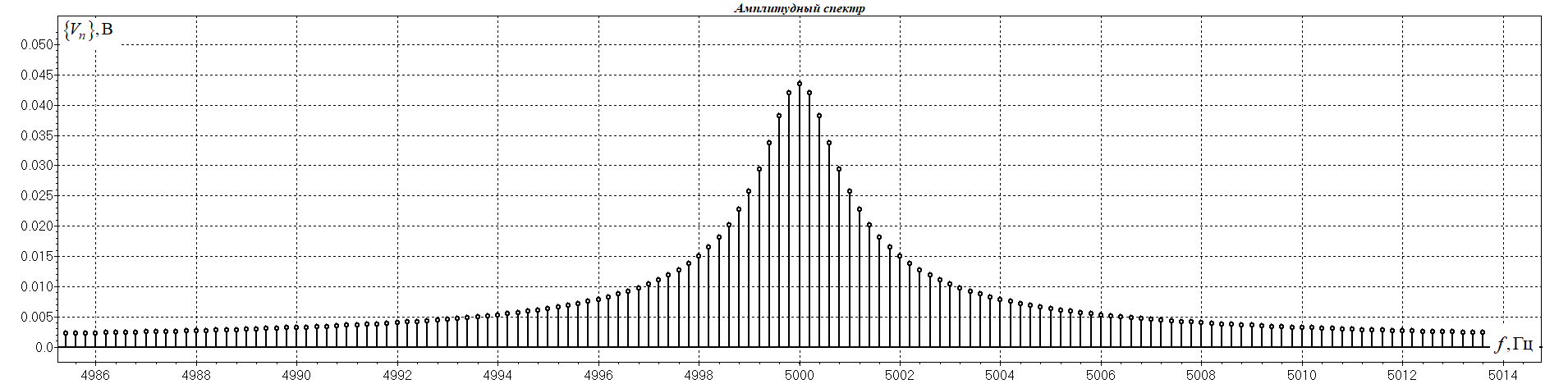 Рисунок 4.5 спектральная диаграмма периодической последовательности экспоненциальных радиоимпульсов t0,01 = 1 с. Q= 5 𝑓0 = 5 кГц  Рисунок 4.6 временная диаграмма фазового спектра экспоненциальных радиоимпульсов t0,01 = 1 с. Q= 5 𝑓0 = 5 кГц 4.3 f-10000  Рисунок 4.7 временная диаграмма периодической последовательности экспоненциальных радиоимпульсов t0,01 = 1 с. Q = 5 𝑓0 = 10 кГц  Рисунок 4.8 спектральная диаграмма периодической последовательности экспоненциальных радиоимпульсов t0,01 = 1 с. Q= 5 𝑓0 = 10 кГц  Рисунок 4.9 временная диаграмма фазового спектра экспоненциальных радиоимпульсов t0,01 = 1 с. Q= 5 𝑓0 = 10 кГц Вывод: амплитудные и фазовые спектры для разных частот схожи. Форма видеосигналов на временной диаграмме аналогична форме огибающей радиоимпульсов, с той лишь разницей, что в случае радиоимпульса участок с амплитудой в 1 В закрашивается чёрным цветом, так как там происходит большое количество колебаний, а не одно. 5. Исследование спектра сигнала с однотональной амплитудной модуляцией (АМ) 5.1. С помощью программы MODUL получили временную и спектральную диаграммы однотонального АМ сигнала с частотой модуляции F = 25 кГц, амплитудой первой гармоники А1 = 0,3 В, устанавливая пределы сетки графика амплитудного спектра 850 < 𝑓 < 1150 кГц. 5.1 Modul F=25 A=0.3 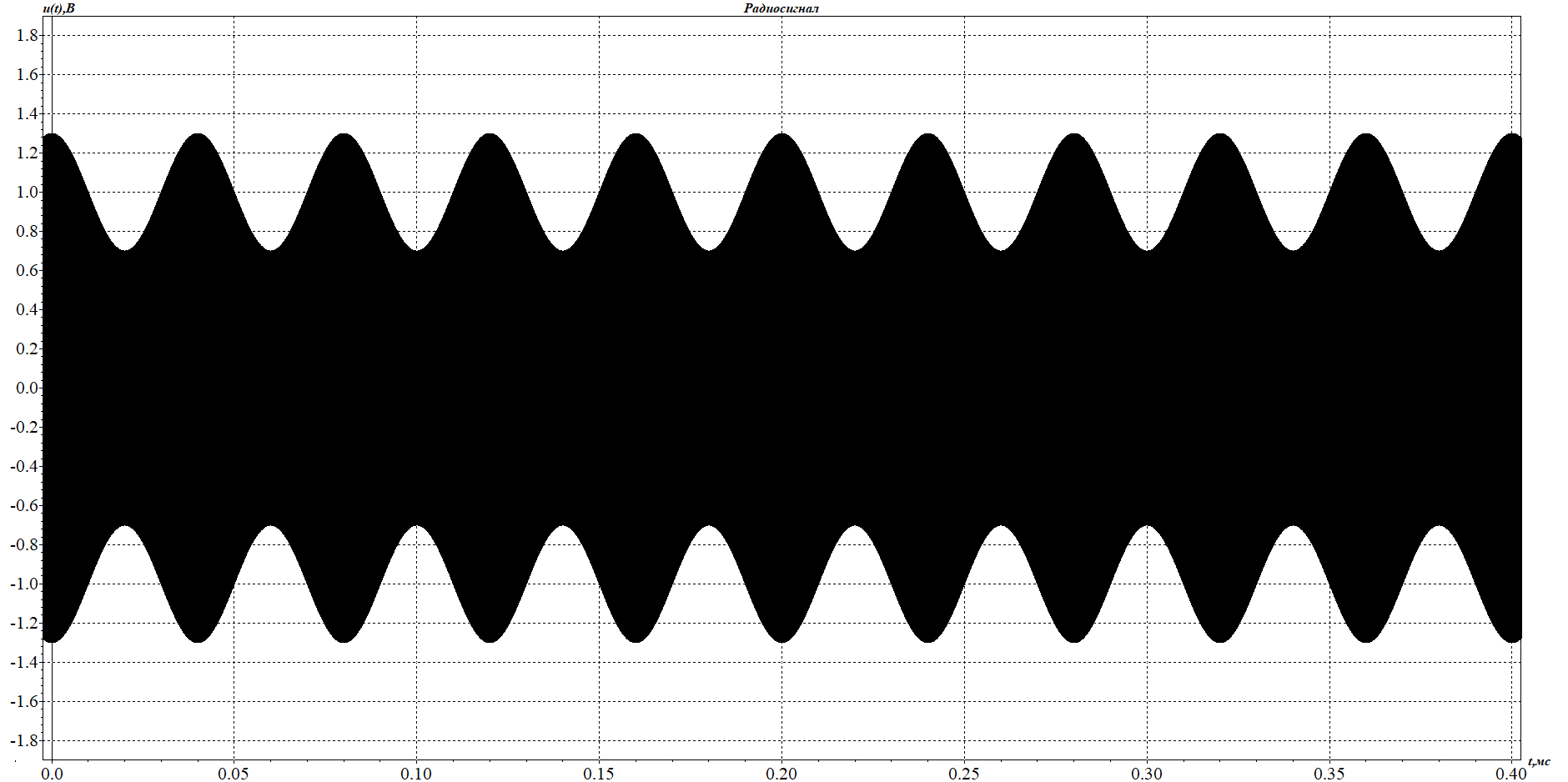 Рисунок 5.1 временная диаграмма однотонального АМ сигнала F = 25 кГц А1 = 0,3 В  Рисунок 5.2 амплитудный спектр однотонального АМ сигнала F = 25 кГц А1 = 0,3 В  Рисунок 5.3 фазовый спектр однотонального АМ сигнала F = 25 кГц А1 = 0,3 В 5.2 A=0.5  Рисунок 5.4 временная диаграмма однотонального АМ сигнала F = 25 кГц А1 = 0,5 В  Рисунок 5.5 амплитудный спектр однотонального АМ сигнала F = 25 кГц А1 = 0,5 В  Рисунок 5.6 фазовый спектр однотонального АМ сигнала F = 25 кГц А1 = 0,5 В 5.2 A=0.7  Рисунок 5.7 временная диаграмма однотонального АМ сигнала F = 25 кГц А1 = 0,7 В  Рисунок 5.8 амплитудный спектр однотонального АМ сигнала F = 25 кГц А1 = 0,7 В  Рисунок 5.9 фазовый спектр однотонального АМ сигнала F = 25 кГц А1 = 0,7 В 5.2 A=1.0  Рисунок 5.10 временная диаграмма однотонального АМ сигнала F = 25 кГц А1 = 1 В 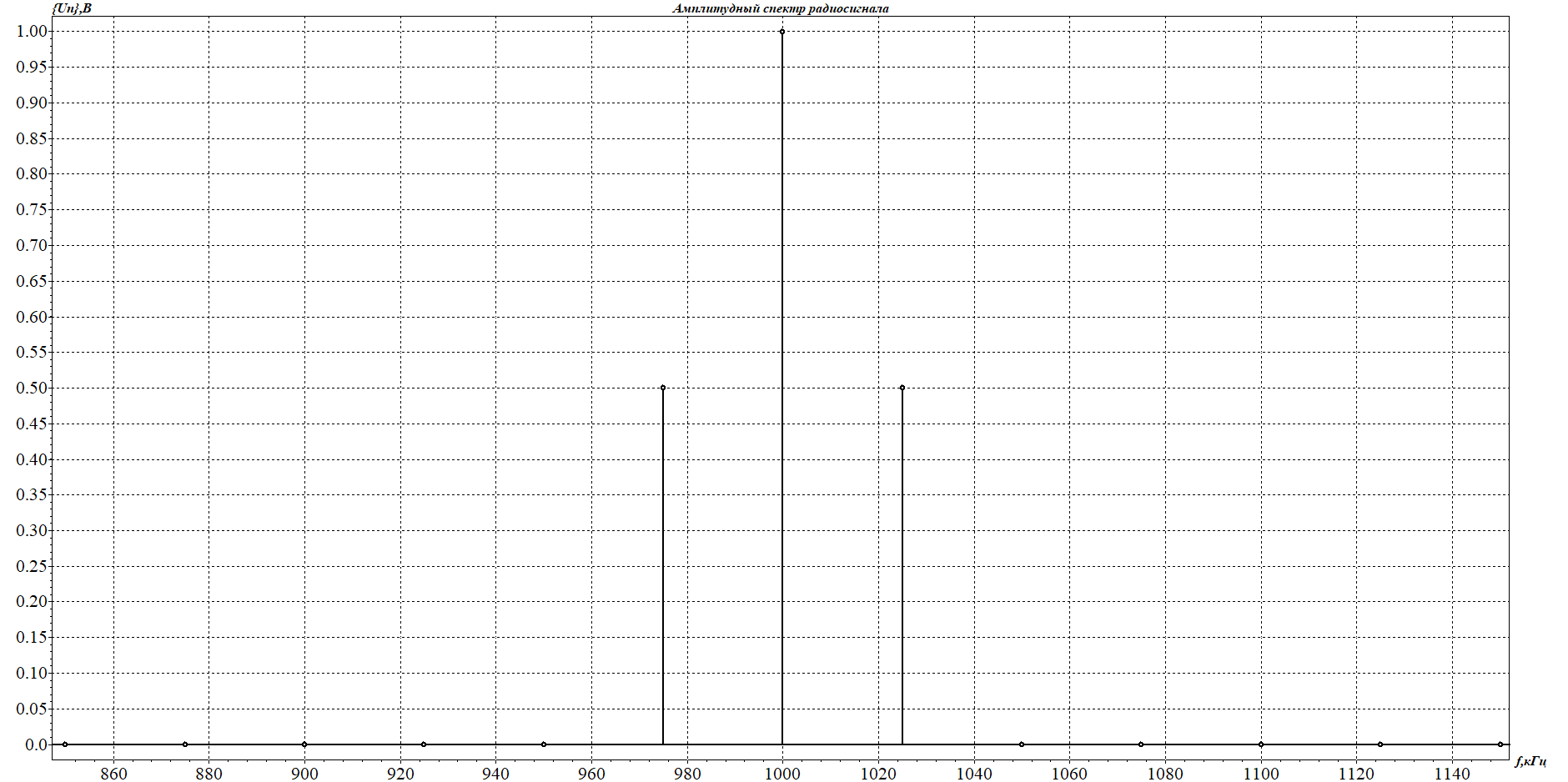 Рисунок 5.11 амплитудный спектр однотонального АМ сигнала F = 25 кГц А1 = 1 В  Рисунок 5.12 фазовый спектр однотонального АМ сигнала F = 25 кГц А1 = 1 В 5.3 Повторить п.5.1-5.2, устанавливая F = 50 кГц.  Рисунок 5.13 временная диаграмма однотонального АМ сигнала F = 50 кГц А1 = 0,3 В  Рисунок 5.14 амплитудный спектр однотонального АМ сигнала F = 50 кГц А1 = 0,3 В 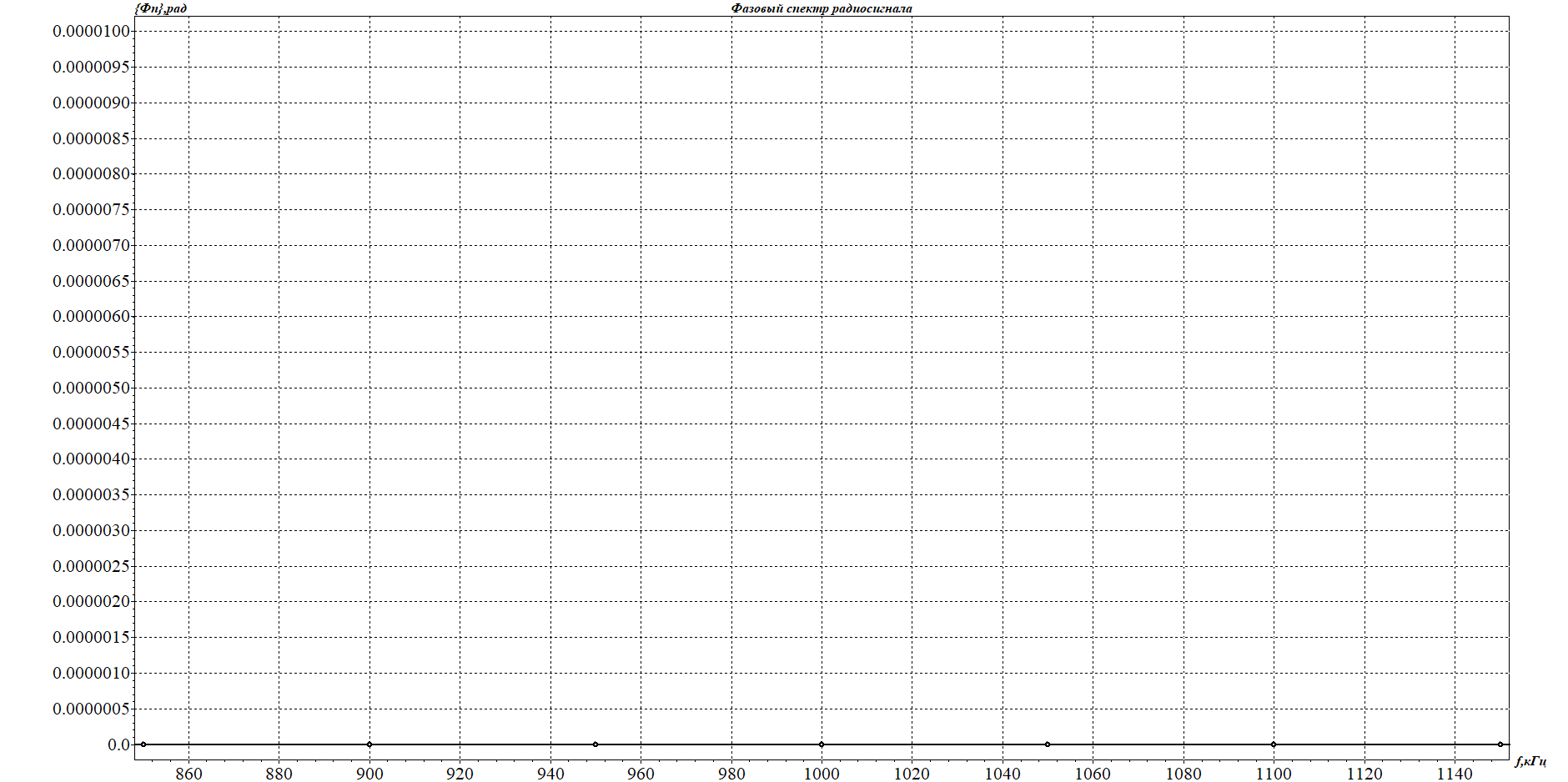 Рисунок 5.14 фазовый спектр однотонального АМ сигнала F = 50 кГц А1 = 0,3 В 5.3 F=50 A=0.5  Рисунок 5.15 временная диаграмма однотонального АМ сигнала F = 50 кГц А1 = 0,5 В 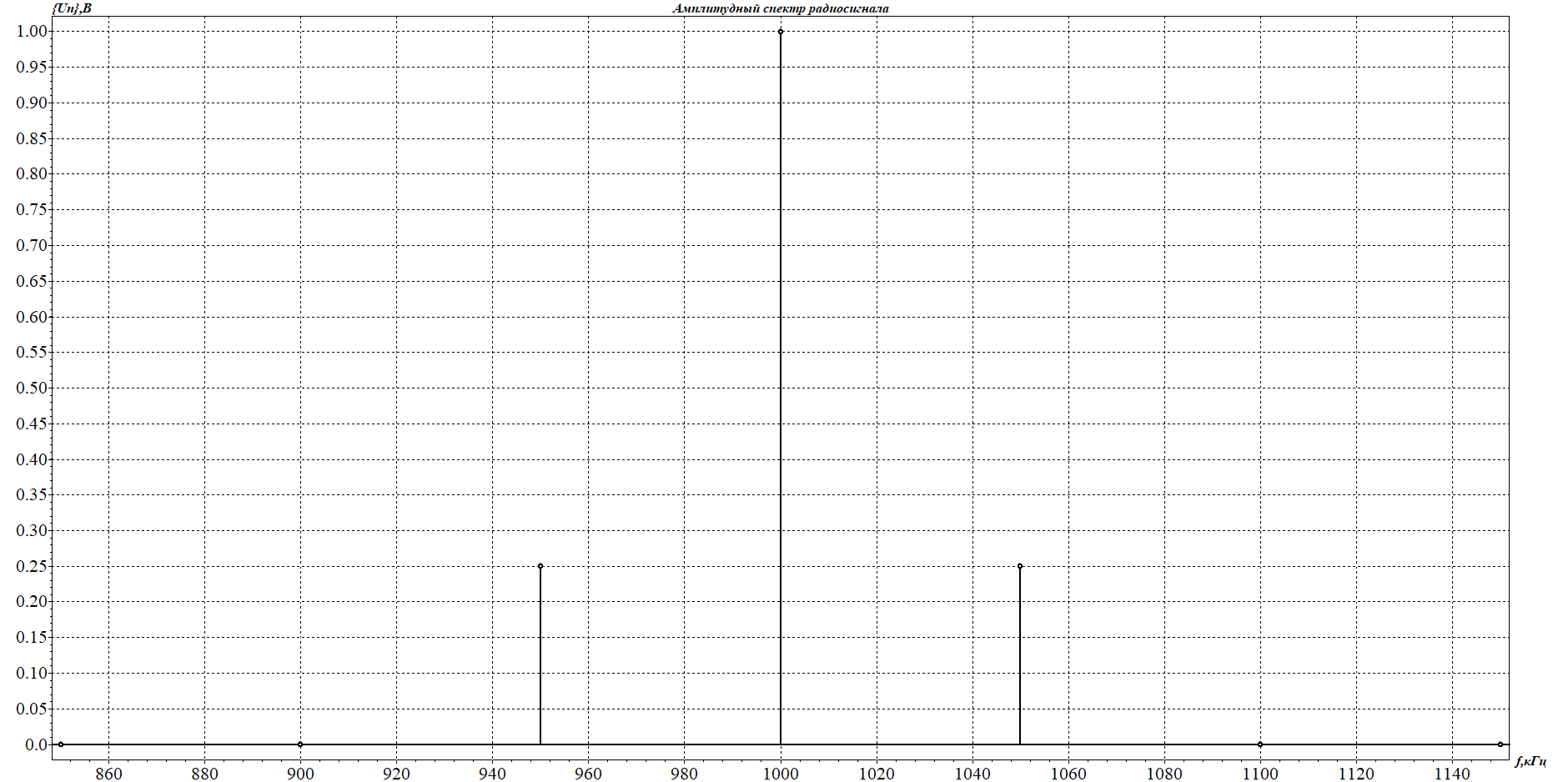 Рисунок 5.16 амплитудный спектр однотонального АМ сигнала F = 50 кГц А1 = 0,5 В  Рисунок 5.17 фазовый спектр однотонального АМ сигнала F = 50 кГц А1 = 0,5 В 5.3 F=50 A=0.7 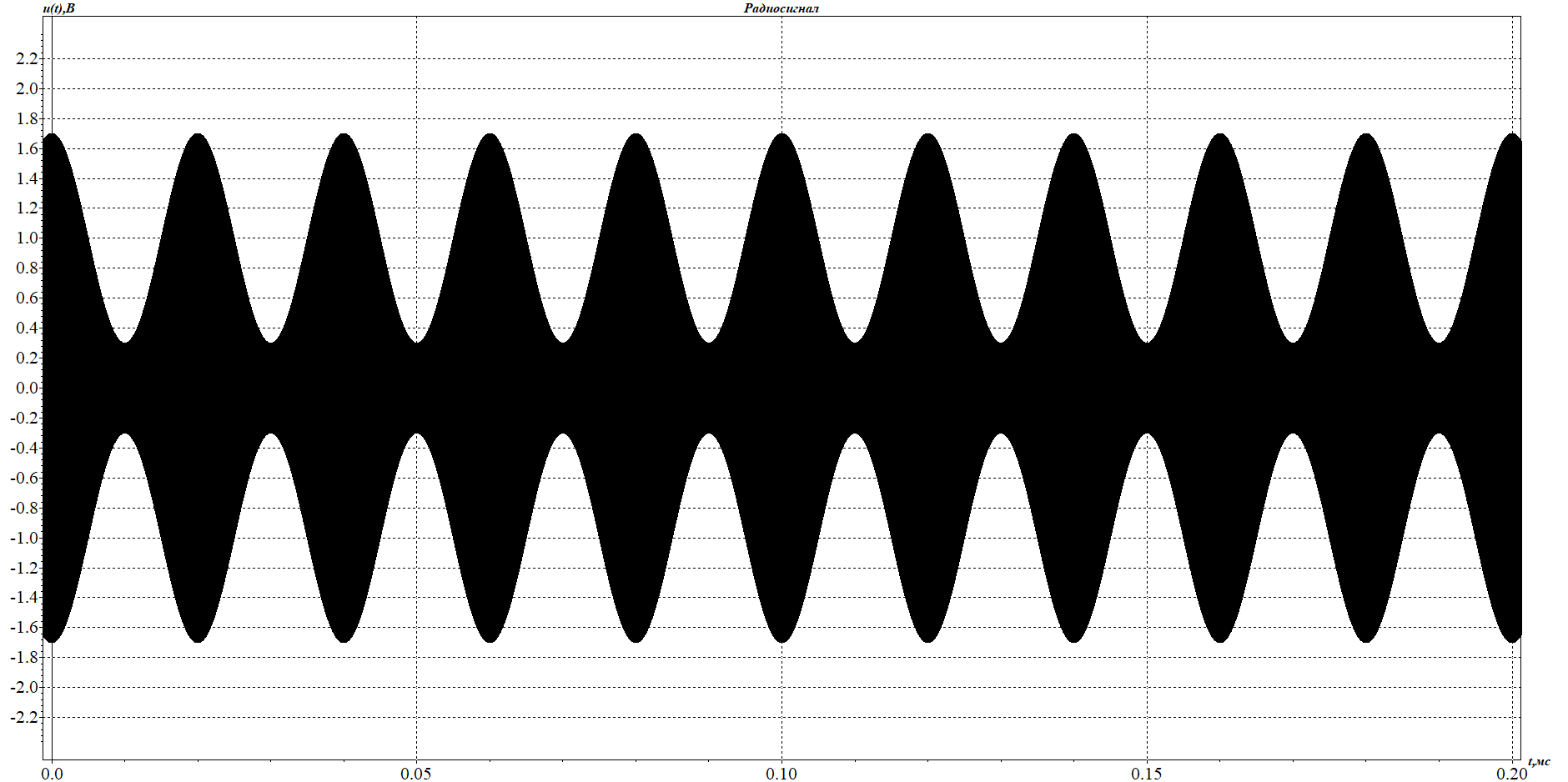 Рисунок 5.18 временная диаграмма однотонального АМ сигнала F = 50 кГц А1 = 0,7 В  Рисунок 5.19 амплитудный спектр однотонального АМ сигнала F = 50 кГц А1 = 0,7 В  Рисунок 5.20 фазовый спектр однотонального АМ сигнала F = 50 кГц А1 = 0,7 В 5.3 F=50 A=1.0  Рисунок 5.21 временная диаграмма однотонального АМ сигнала F = 50 кГц А1 = 1 В 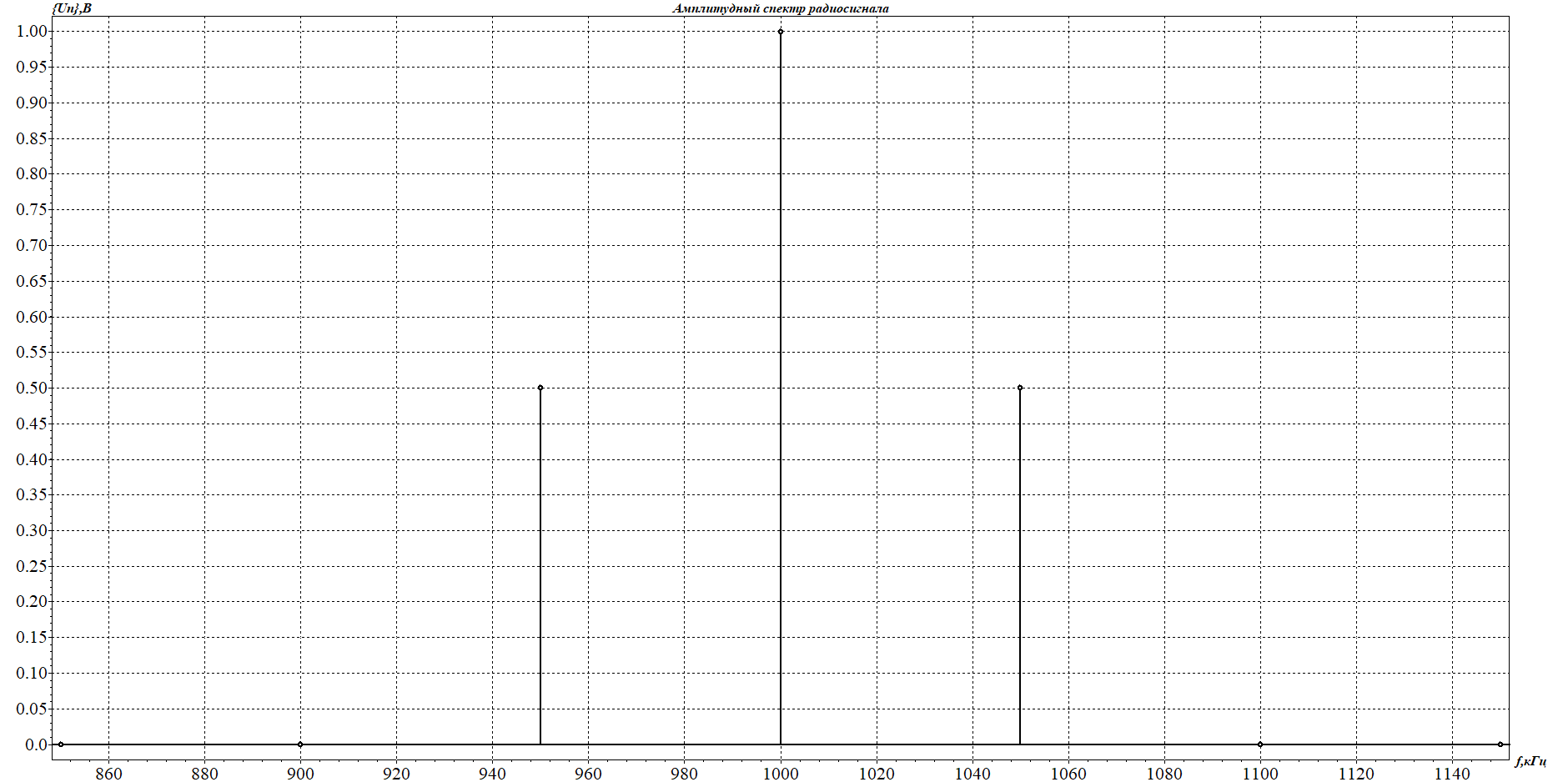 Рисунок 5.22 амплитудный спектр однотонального АМ сигнала F = 50 кГц А1 = 1 В  Рисунок 5.23 фазовый спектр однотонального АМ сигнала F = 50 кГц А1 = 1 В 5.4. Вывод: чем больше значение коэффициента модуляции, тем больше амплитуда боковых гармоник и тем больше разница между максимальным и минимальным отклонением огибающей от нуля. Чем выше частота модуляции, тем шире амплитудный спектр сигналов. 6. Исследование спектра сигнала с двухтональной амплитудной модуляцией 6.1. С помощью программы MODUL получить и поместить в отчёт временную и спектральную диаграммы двухтонального АМ сигнала с частотами модуляции F1 = 25 кГц, F2 = 50 кГц и амплитудами гармоник модулирующего колебания А1 = 0,5, А2 = 0,3. Частоты гармоник кратны частоте первой гармоники как nF1, где n – номер гармоники.  Рисунок 6.1 временная диаграмма двухтонального АМ сигнала F1 = 25 кГц, F2 = 50 кГц, А1 = 0,5, А2 = 0,3  Рисунок 6.2 спектральная диаграмма двухтонального АМ сигнала F1 = 25 кГц, F2 = 50 кГц, А1 = 0,5, А2 = 0,3 6.2. Повторить п.6.1, устанавливая F1 = 25 кГц, F2 = 50 кГц, А1 = 0,3, А2 = 0,5. 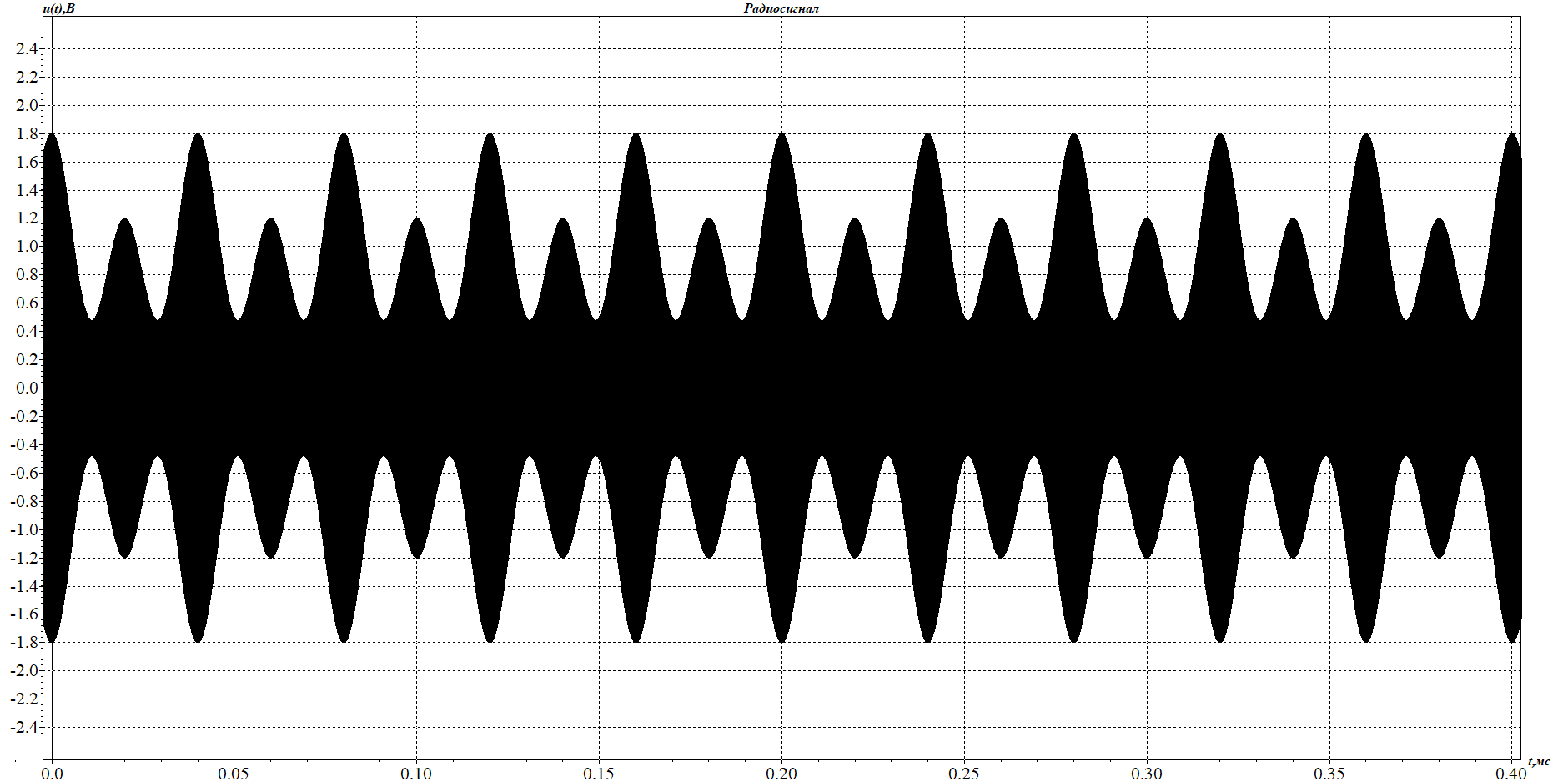 Рисунок 6.3. временная диаграмма двухтонального АМ сигнала F1 = 25 кГц, F2 = 50 кГц, А1 = 0,3, А2 = 0,5 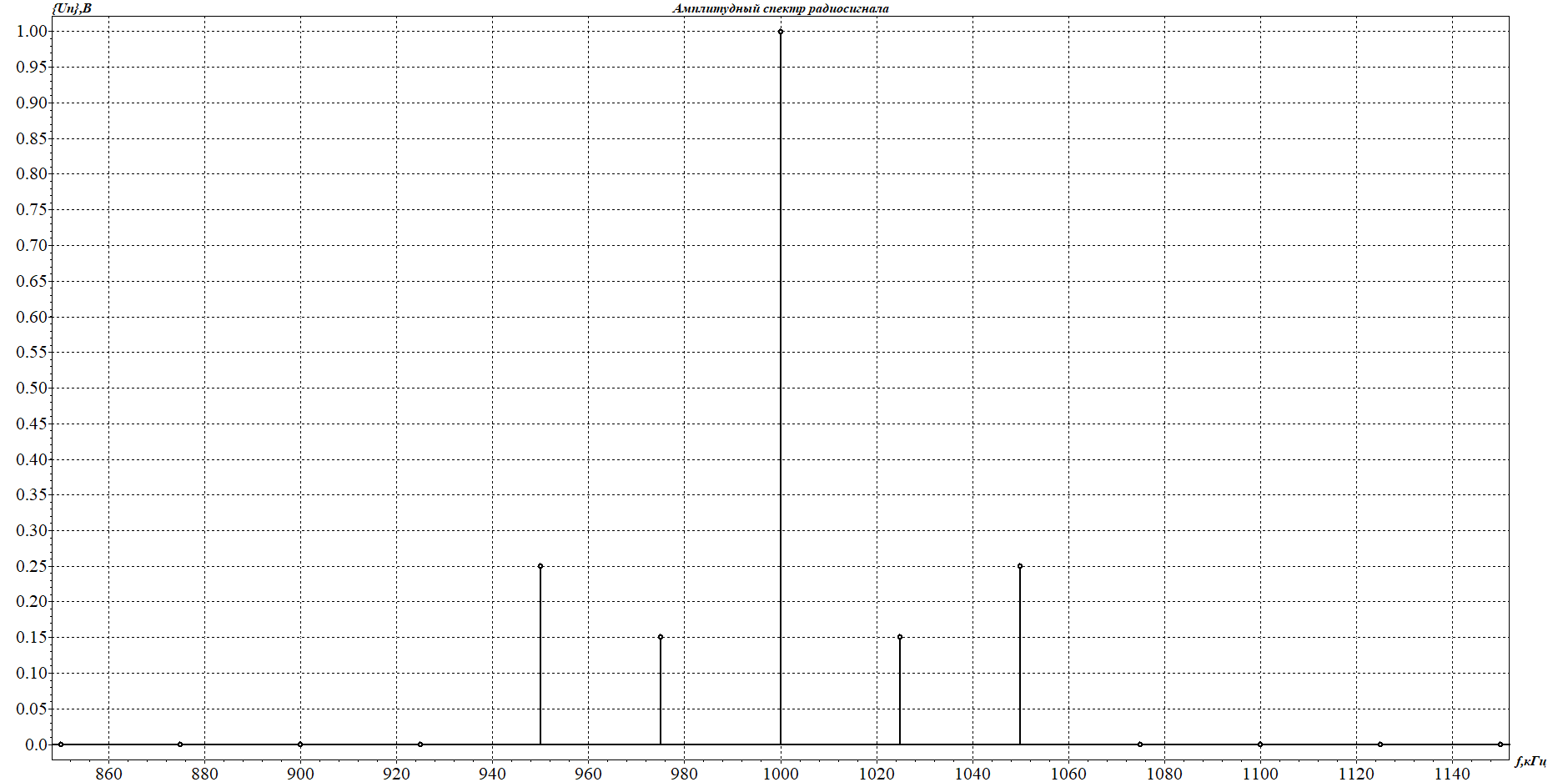 Рисунок 6.4 спектральная диаграмма двухтонального АМ сигнала F1 = 25 кГц, F2 = 50 кГц, А1 = 0,3, А2 = 0,5 6.3. Повторить п.6.1, устанавливая F1 = 25 кГц, F3 = 75 кГц, А1 = 0,5, А3 = 0,3.  Рисунок 6.5 временная диаграмма двухтонального АМ сигнала F1 = 25 кГц, F3 = 75 кГц, А1 = 0,5, А2 = 0,3  Рисунок 6.6 спектральная диаграмма двухтонального АМ сигнала F1 = 25 кГц, F3 = 75 кГц, А1 = 0,5, А2 = 0,3 6.3. Повторить п. 6.1-6.2 установив для 2-ой гармоники начальную фазу 45°. Получить фазовый спектр сигнала, поместить в отчёт. F1 = 25 кГц, F2 = 50 кГц А1 = 0,5, А2 = 0,3 45°(0.7854 рад) 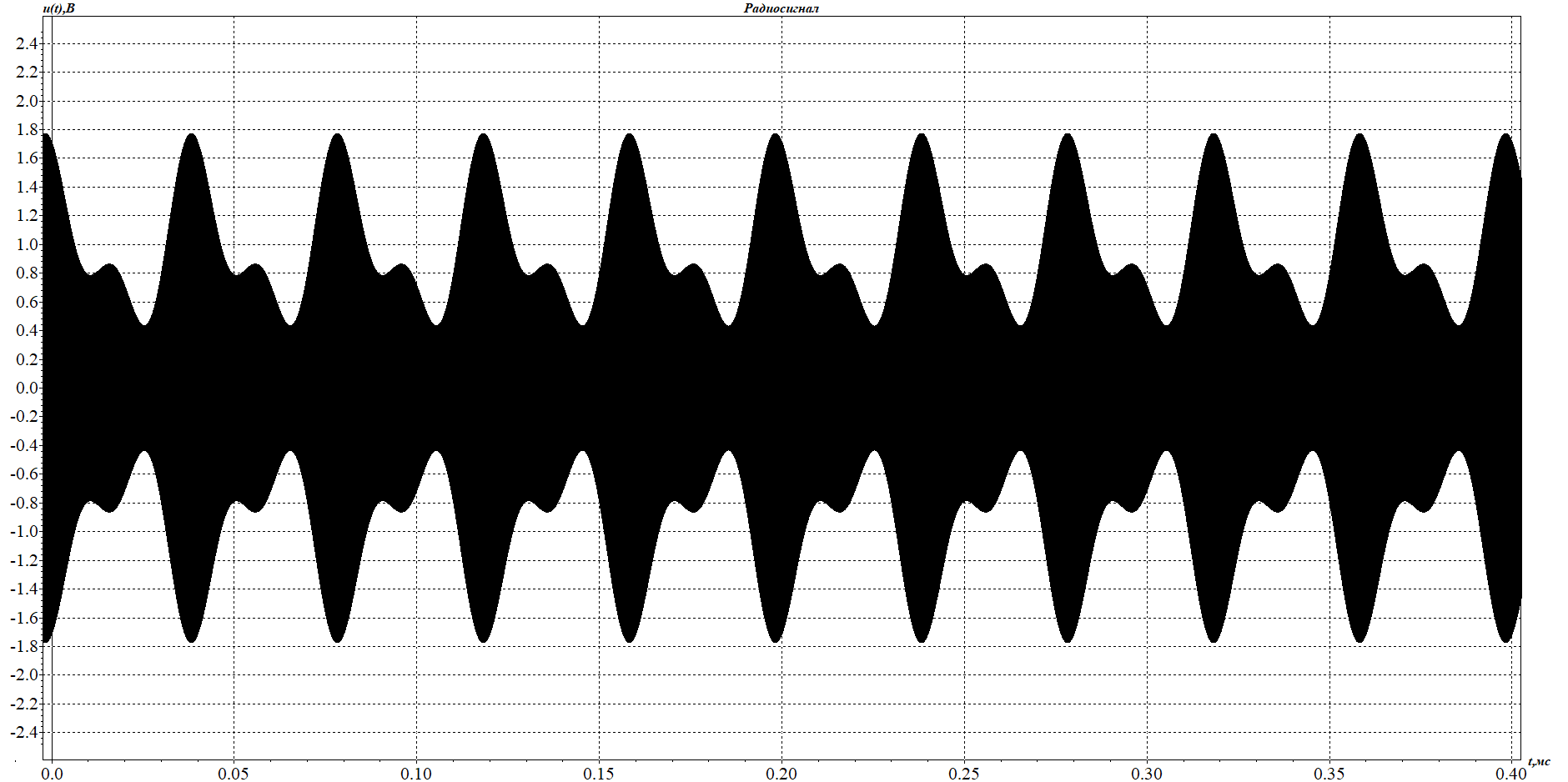 Рисунок 6.7 временная диаграмма двухтонального АМ сигнала F1 = 25 кГц, F2 = 50 кГц, 𝜑2=45°, А1 = 0,5, А2 = 0,3  Рисунок 6.8 спектральная диаграмма двухтонального АМ сигнала F1 = 25 кГц, F2 = 50 кГц, 𝜑2=45°, А1 = 0,5, А2 = 0,3 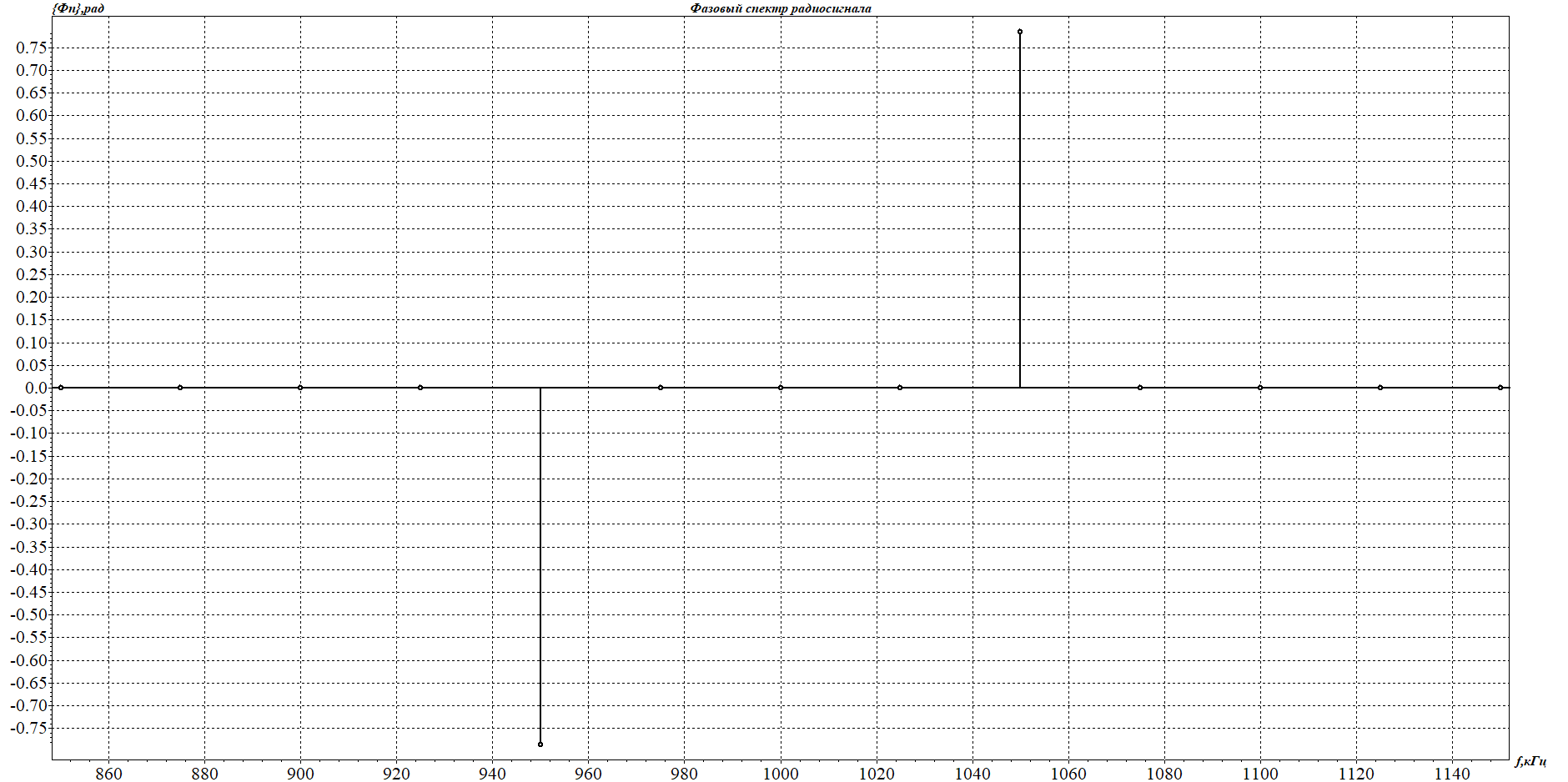 Рисунок 6.9 фазовый спектр АМ сигнала F1 = 25 кГц, F2 = 50 кГц, 𝜑2=45°, А1 = 0,5, А2 = 0,3  Рисунок 6.10 временная диаграмма двухтонального АМ сигнала F1 = 25 кГц, F2 = 50 кГц, 𝜑2=45°, А1 = 0,3, А2 = 0,5  Рисунок 6.11 спектральная диаграмма двухтонального АМ сигнала F1 = 25 кГц, F2 = 50 кГц, 𝜑2=45°, А1 = 0,3, А2 = 0,5  Рисунок 6.12 фазовый спектр АМ сигнала F1 = 25 кГц, F2 = 50 кГц,𝜑2=45°, А1 = 0,3, А2 = 0,5 6.3 F1 = 25 кГц, F3 = 75 кГц, А1 = 0,5, А3 = 0,3 45°(0.7854 рад)  Рисунок 6.13 временная диаграмма двухтонального АМ сигнала F1 = 25 кГц, F3 = 75 кГц, 𝜑2=45°, А1 = 0,5, А3 = 0,3  Рисунок 6.14 спектральная диаграмма двухтонального АМ сигнала F1 = 25 кГц, F3 = 75 кГц, 𝜑2=45°, А1 = 0,5, А2 = 0,3  Рисунок 6.15 фазовый спектр АМ сигнала F1 = 25 кГц, F3 = 75 кГц,𝜑2=45°, А1 = 0,5, А2 = 0,3 Вывод: чем больше амплитуда второй и/или третьей гармоники, тем больше становится амплитуда боковых полос, тем больше разница между максимальным и минимальным отклонениями огибающей от нуля. Появление у второй гармоники ненулевой начальной фазы сдвигает на временной диаграмме колебания с меньшей амплитудой и изменяет форму огибающей 7. Исследование спектра сигнала с однотональной частотной модуляцией 7.1. С помощью программы MODUL получили амплитудного спектра сигнала с тональной частотной модуляцией (ЧМ) с частотой модуляции F = 1 кГц и амплитудами первой гармоники модулирующего колебания, приведёнными в первой строке таблице 1.  Рисунок 7.1. Амплитудный спектр при U = 0 В  Рисунок 7.2. Амплитудный спектр при U = 0,1 В  Рисунок 7.3. Амплитудный спектр при U = 0,5 В  Рисунок 7.4. Амплитудный спектр при U = 0,7 В  Рисунок 7.5. Амплитудный спектр при U = 1,0 В  Рисунок 7.6. Амплитудный спектр при U = 3,0 В 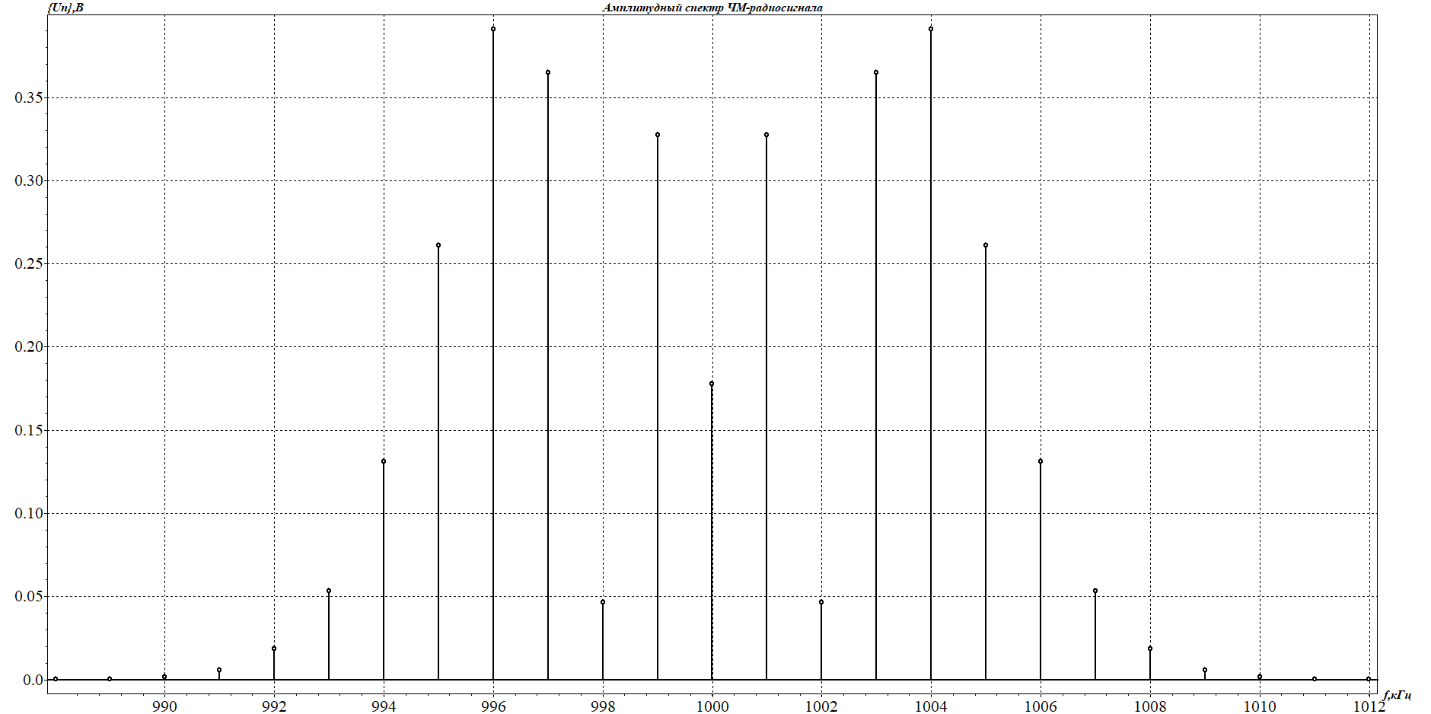 Рисунок 7.7. Амплитудный спектр при U = 5,0 В  Рисунок 7.8. Амплитудный спектр при U = 7,0 В  Рисунок 7.9. Амплитудный спектр при U = 10,0 В  Рисунок 7.10. Амплитудный спектр при U = 15,0 В 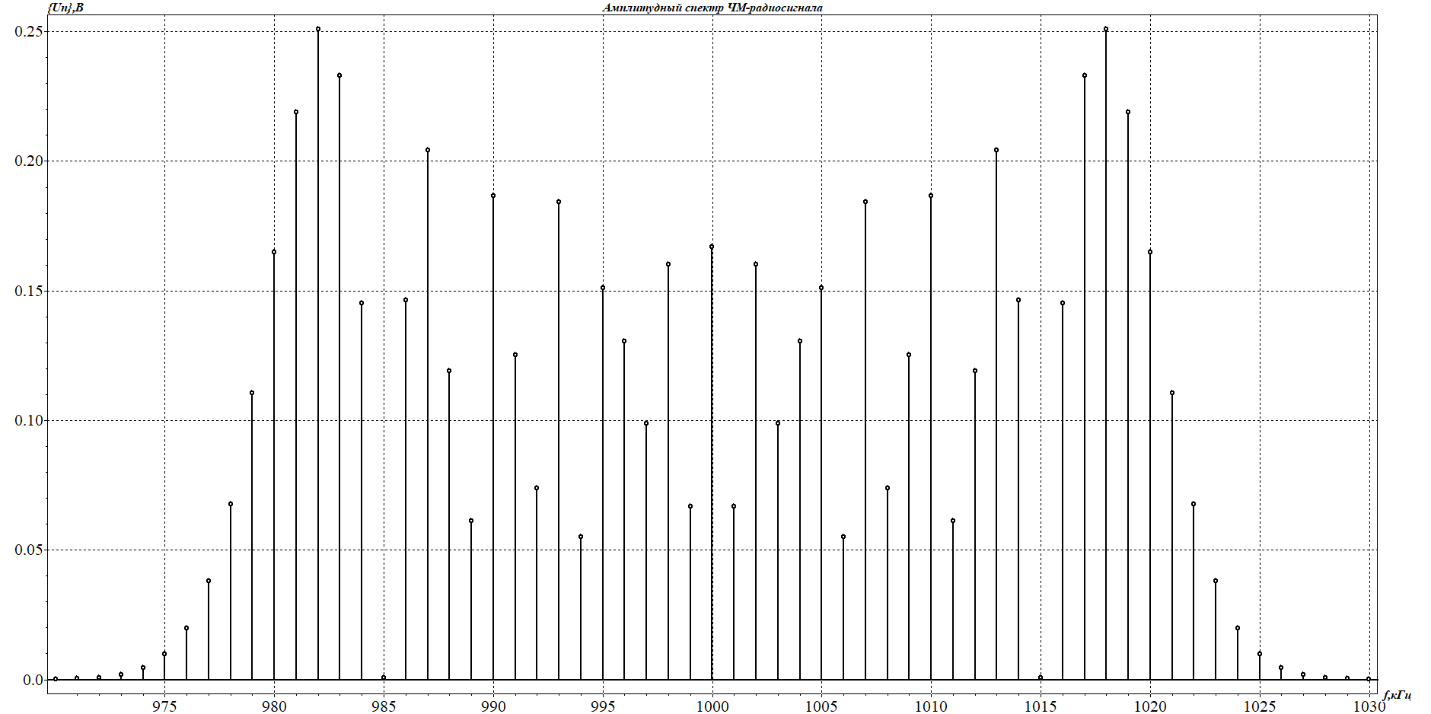 Рисунок 7.11. Амплитудный спектр при U = 20,0 В  Рисунок 7.12. Амплитудный спектр при U = 25,0 В 7.2. По спектральным диаграммам определили ширину спектра ЧМ сигнала  , занесли полученные значения в соответствующие ячейки таблицы 1. , занесли полученные значения в соответствующие ячейки таблицы 1.Таблица 1. Зависимость ширины спектра от амплитуды модулирующего колебания.
7.3. Рассчитали отношение  /F для третьей строчки таблицы 1 и построили график зависимости относительной ширины спектра от индекса модуляции /F для третьей строчки таблицы 1 и построили график зависимости относительной ширины спектра от индекса модуляции  /F = /F =  (А)/F. (А)/F.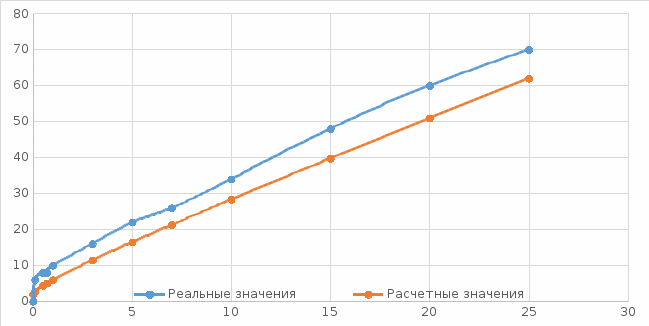 7.4. Вывод: ширина спектра ЧМ сигнала увеличивается с увеличением индекса модуляции. 8. Исследование спектра сигнала с двухтональной частотной модуляцией 8.1. С помощью программы MODUL получить и поместить в отчёт графики мгновенной частоты и амплитудного спектра сигнала с двухтональной частотной модуляцией с частотами модуляции F1 = 15 кГц , F2 = 30 кГц и парциальными индексами модуляции m1 = 5 , m2 = 3.  Рисунок 8.1 график мгновенной частоты сигнала F1=15 кГц, F2 = 30 кГц, m1 = 5, m2 = 3  Рисунок 8.2 график амплитудного спектра сигнала F1=15 кГц, F2 = 30 кГц, m1 = 5, m2 = 3 8.2. Повторить п.9.1, устанавливая F1 =15 кГц, F2 = 30 кГц, m1 = 3 , m2 = 5.  Рисунок 8.3 график мгновенной частоты сигнала F1=15 кГц, F2 = 30 кГц, m1 = 3, m2 = 5 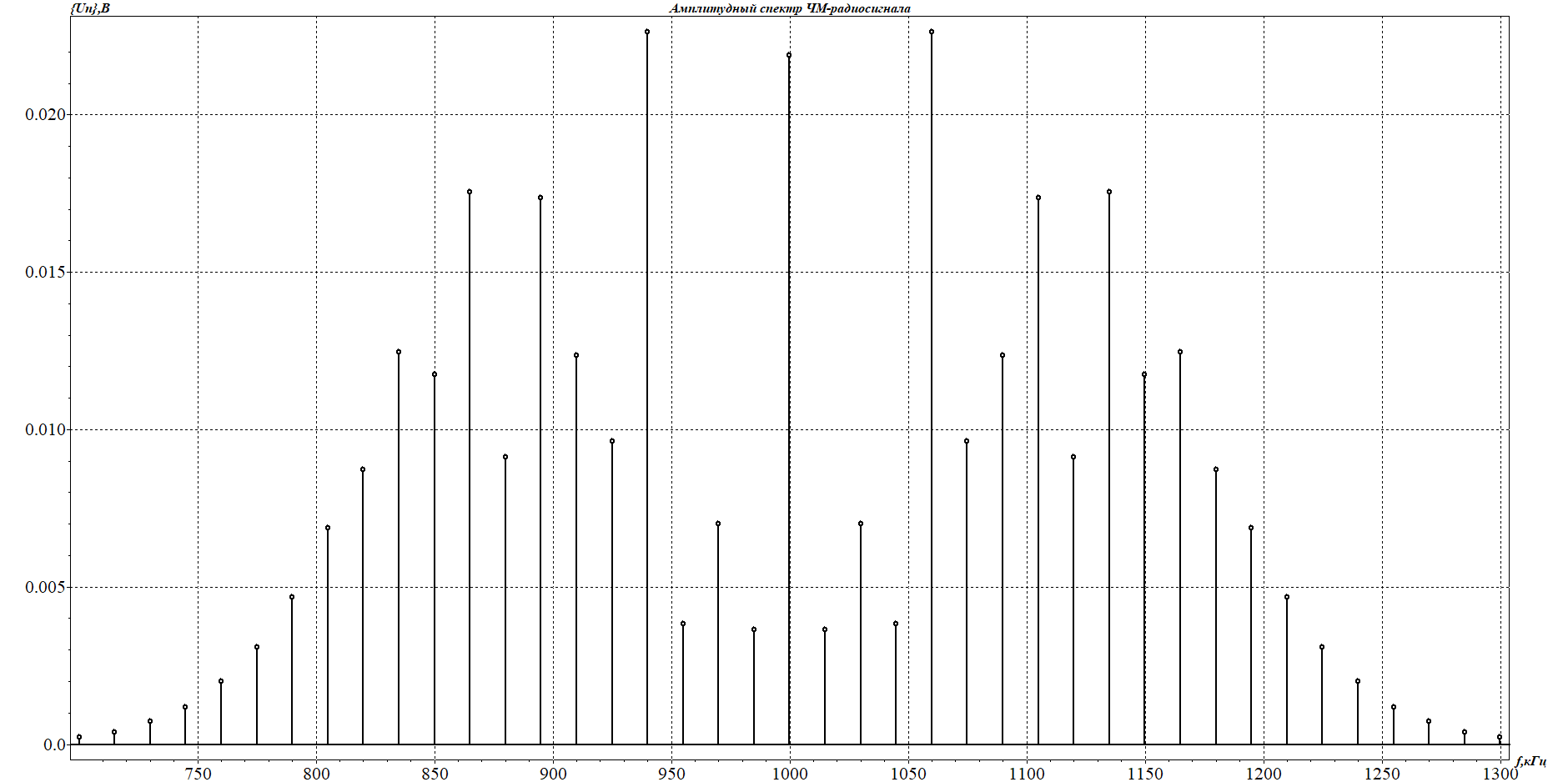 Рисунок 8.4 график амплитудного спектра сигнала F1=15 кГц, F2 =30 кГц, m1 = 3, m2 = 5 8.3. Повторить п.9.1, устанавливая F1 = 15 Гц , F2 =45 кГц , m1 = 5 , m2 = 3.  Рисунок 8.5 график мгновенной частоты сигнала F1=15 кГц, F2 = 45 кГц, m1 = 5, m2 = 3  Рисунок 8.6 график амплитудного спектра сигнала F1=15 кГц, F2 = 45 кГц, m1 = 5, m2 = 3 8.4. Вывод: амплитудный спектр ЧМ сигнала зависит от парциальных индексов модуляции. Вывод: в данной лабораторной работе мы изучили спектры радиосигналов, однотональную и двухтональную амплитудную и частотную модуляции. |

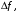 кГц
кГц