СИНТЕЗ И ИССЛЕДОВАНИЕ АСИНХРОННЫХ ПОСЛЕДОВАТЕЛЬНОСТНЫХ СХЕМ СИСТЕМ УПРАВЛЕНИЯ. СИНТЕЗ И ИССЛЕДОВАНИЕ АСИНХРОННЫХ ПОСЛЕДОВАТЕЛЬНОСТНЫХ СХЕМ СИСТ. Исследование асинхронных последовательностных схем систем управления
 Скачать 336.75 Kb. Скачать 336.75 Kb.
|
|
КОНТРОЛЬНАЯ РАБОТА СИНТЕЗ И ИССЛЕДОВАНИЕ АСИНХРОННЫХ ПОСЛЕДОВАТЕЛЬНОСТНЫХ СХЕМ СИСТЕМ УПРАВЛЕНИЯ Вариант 2 Разработать схему управления транспортным манипулятором линии гальванической обработки так, чтобы после стартового сигнала кассета поднялась из положения 1 в положение 2, затем переместилась из положения 3 в положение 4, опустилась в положение 1 и после пятисекундной паузы поднялась из положения 1 в положение 2, затем переместилась из положения 4 в положение 6, опустилась в положение 1 и возвратилась в исходное положение. Управляется и контролируется устройство через блок сопряжения. Исходя из этого, был разработан граф работы системы. Пояснения к графу приведены ниже рисунка. 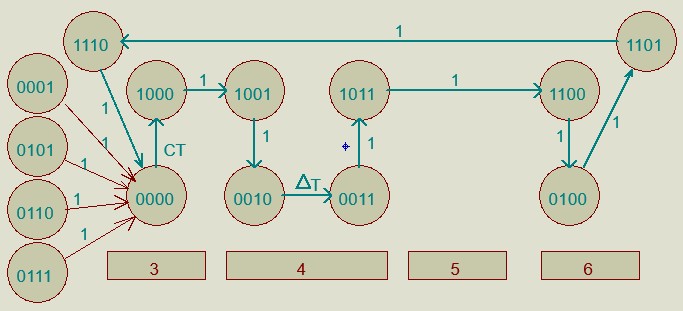 За вторичные функции принимаем ABCD, то есть 4 разряда. Разряд А это состояние поднято/опущено. Поднято – 1, опущено – 0. Работа начинается с состояния 0000, затем по команде “старт” кассета поднимается и состояние становится 1000. Происходит перемещение из положения 3 в положение 4, при этом состояние меняется на 1001. Далее кассета опускается, и состояние становится 0010. После паузы в 5 секунд состояние становится 0011, затем происходит подъем и смена состояния на 1011. Затем происходит перемещение из 4 в 6 позицию и состояние становится 1100. После этого опускаемся вниз, и имеем состояние 0100. Далее происходит подъем и смена состояния на 1101. После чего возвращаемся на 3 позицию – 1110 и опускаемся в исходное положение – 0000. Если формально следовать заданию, то можно было сократить количество переменных, но с опущенной кассетой ездить невозможно, поэтому переменных получилось 4. Несколько состояний в работе схемы не используются. Но возможно случайное попадание системы в эти состояния. Во избежание “зависания” в случае попадания в эти состояния система переходит в исходное состояние. Далее на рисунках выделены области, где переменные A, B, C, D равны 1. Затем для переменных A, B, C, D производится запись логических выражений, устанавливающих и сбрасывающих соответствующий триггер, и приводится схема, реализующая это выражение. 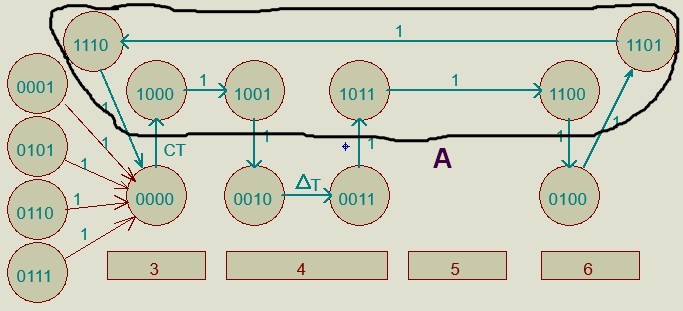 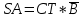 * *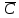 * * 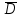 + +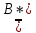 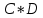 + + 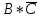 * * 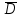 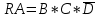 + + 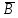 * * 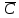 * * 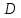 + + 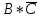 * * 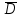 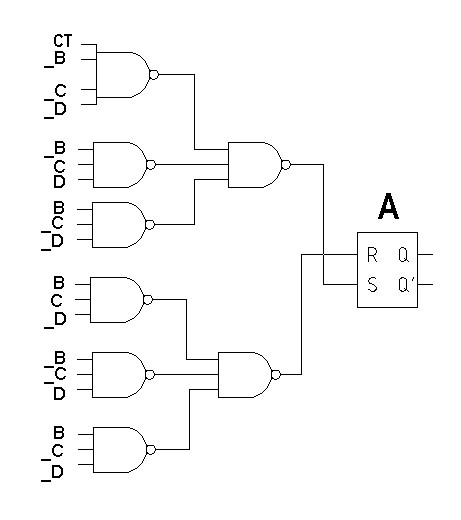 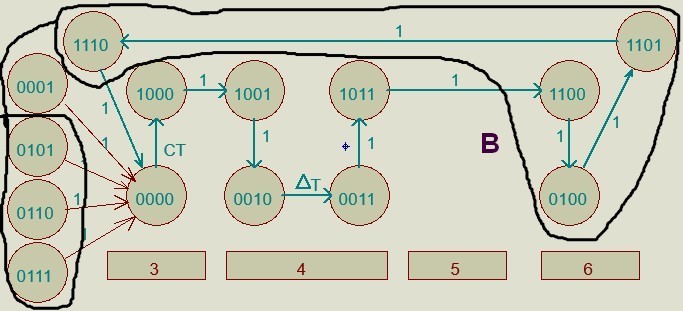 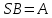 * * 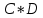 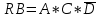 + + 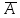 * *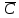 * *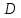 + + 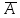 * *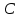 * * 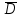 + + 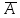 * *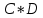 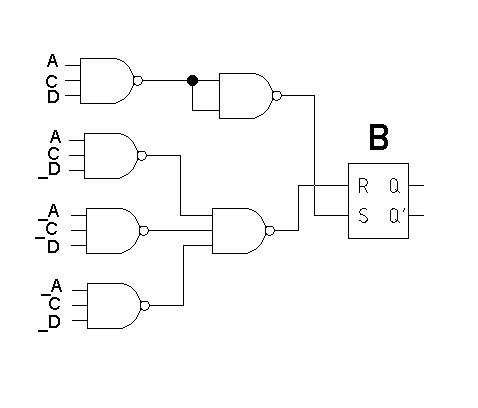 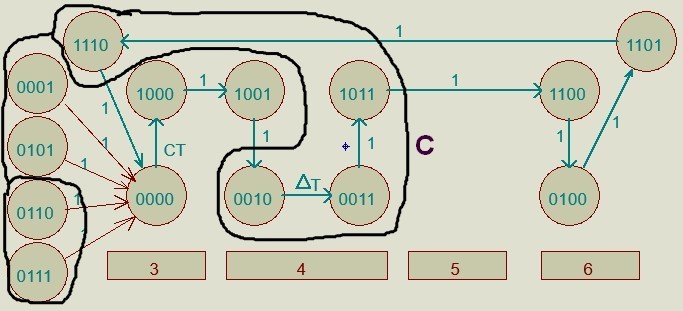 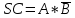 * * 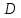 + + 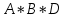 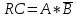 * * 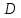 + + 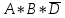 + + 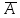 * *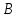 * *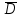 + + 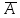 * *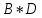 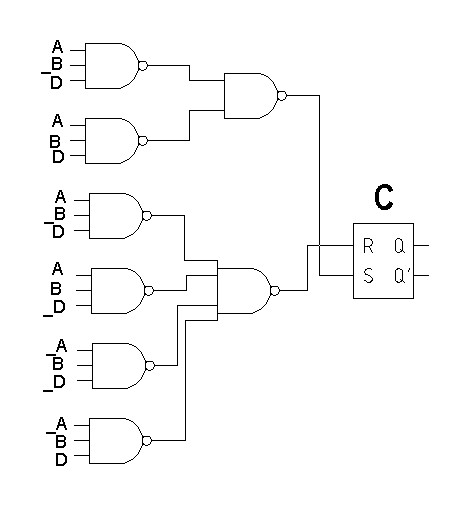 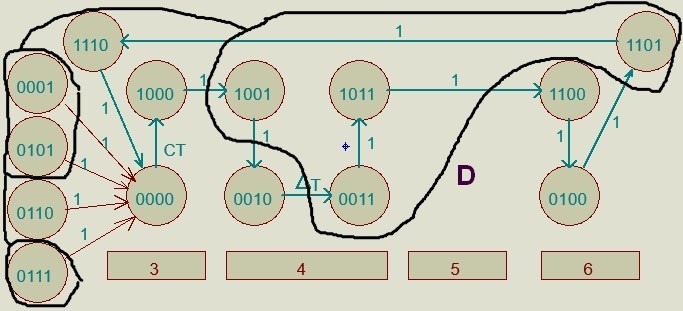 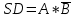 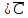 + + 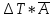 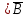 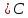 + + 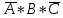 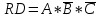 + +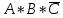 + +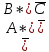 + + 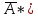 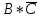 + +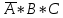 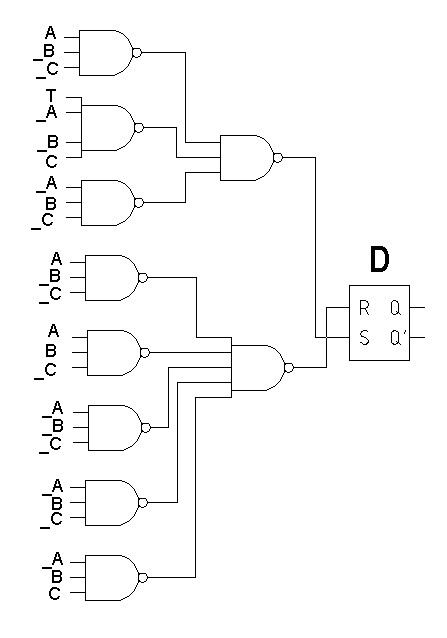 |
