Лабораторная работа №1. Лр 1. Исследование цепей синусоидального тока с конденсатором и индуктивной катушкой

• Название: Исследование цепей синусоидального тока с конденсатором и индуктивной катушкой
• Анкор: Лабораторная работа №1
• Дата: 18.02.2023
• Размер: 269.24 Kb.
• Имя файла: Лр 1.docx
• Тип: Исследование; #942846

ЛАБОРАТОРНАЯ РАБОТА 1

Исследование цепей синусоидального тока с конденсатором и индуктивной катушкой
Цель – исследование режимов работы цепей синусоидального тока с

последовательным и параллельным соединениями конденсатора и индуктивной катушки.
Задание

1. Исследовать неразветвленную цепь синусоидального тока, содержащую

конденсатор и индуктивную катушку, в трех режимах:



2. Исследовать разветвленную цепь синусоидального тока с параллельным

соединением конденсатора и индуктивной катушки в трех режимах:



3. Построить векторные диаграммы напряжений и токов для всех режимов

работы цепи с последовательным и параллельным соединением

конденсатора и индуктивной катушки.

4. Рассчитать для каждого режима параметры цепи (табл. 1 и 2).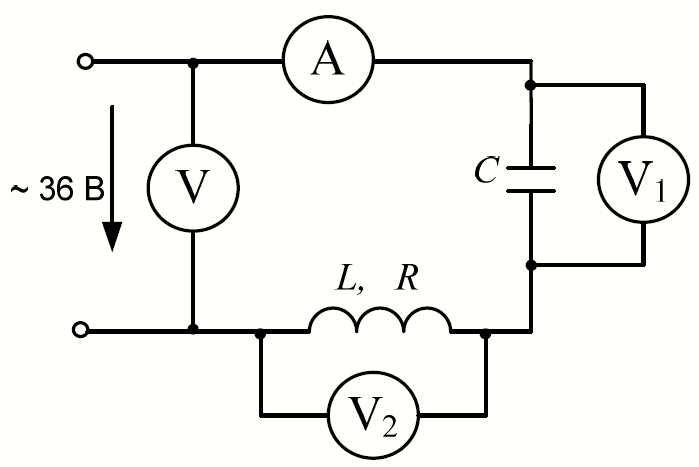



Рис 1

1. Соберём схему согласно Рис 1 и будем изменять ёмкость, показания приборов внесём в таблицу 1
Таблица 1

Режим	Данные измерений				Данные из векторных диаграмм
	I	U	U1	U2		UR	UL	φ
	A	B	B	B		B	B	Град
1	0,108	36	68,02	36,81		13,0	36,0	-69
2	0,300	36	94,19	101,96		36	95	0
3	0,147	36	15,39	49,99		17,6	50,0	61

По результатам экспериментальных данных произведём расчёт полного сопротивления цепи и определим коэффициент мощности для всех значений ёмкости

Первый опыт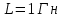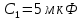





Индуктивное сопротивление катушки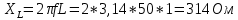



Ёмкостное сопротивление конденсатора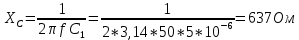



Реактивное сопротивление цепи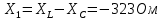



Полное сопротивление цепи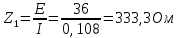



Коэффициент мощности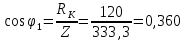



Второй опыт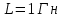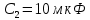





Индуктивное сопротивление катушки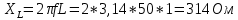



Ёмкостное сопротивление конденсатора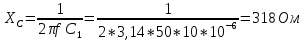



Реактивное сопротивление цепи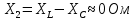



Полное сопротивление цепи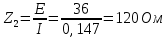



Коэффициент мощности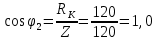



Третий опыт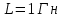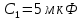





Индуктивное сопротивление катушки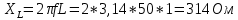



Ёмкостное сопротивление конденсатора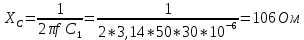



Реактивное сопротивление цепи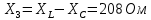



Полное сопротивление цепи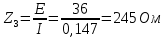



Коэффициент мощности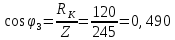

Режим	Результаты вычислений
	R	XL	XC	X	Z	C	L	cosφ
	Ом	Ом	Ом	Ом	Ом	мкФ	Гн	-
1	120	314	637	-323	333б3	5	1	0,360
2	120	314	318	0	120	10	1	1,0
3	120	314	106	208	245	30	1	0,490

Построим векторные диаграммы последовательной цепи при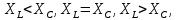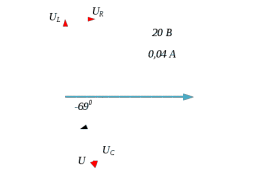




Рис 2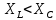



Рис 3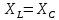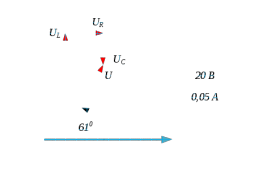


Рис 4.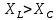

Выводы: Если индуктивное сопротивление меньше ёмкостного сопротивления, то вектор тока опережает вектор приложенного напряжения, если индуктивное сопротивление больше ёмкостного сопротивления, то вектор тока отстаёт от вектора приложенного напряжения, если индуктивное сопротивление равно ёмкостному сопротивлению, то в цепи наблюдается резонанс напряжений и величина тока будет иметь наибольшую величину.

2.Соберём схему по заданным параметрам (Рис 5). Произведём измерения в электрической цепи, изменяя ёмкость конденсатора. Результаты измерений внесём в таблицу 3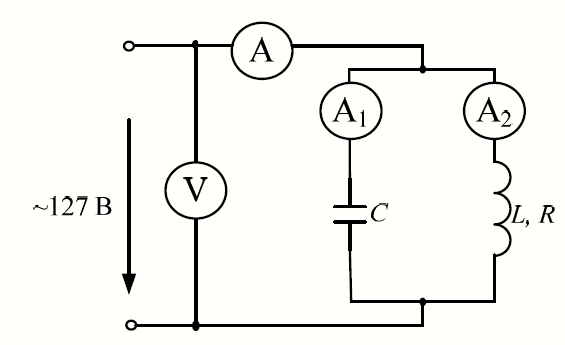



Рис 5

Таблица 3

Режим	Данные измерений				Данные из векторных диаграмм
	U	I	I1	I2	Ia	Ip	I2C	I2L	φ
	B	A	A	A	A	A	A	A	град
1	127	0,273	0,081	0,338	0,180	0,206	0,08	0,340	48
2	127	0,180	0,283	0,338	0,180	0,0	0,280	0,340	0,0
3	127	0,367	0,606	0,338	0,180	0,310	0,600	0,340	60

По результатам экспериментальных данных произведём вычисления проводимостей во всех опытах и определим коэффициент мощности.

Первый опыт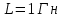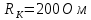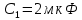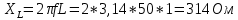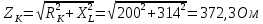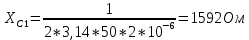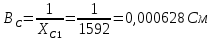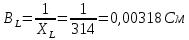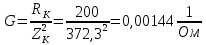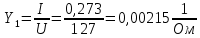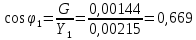























Второй опыт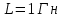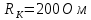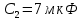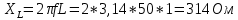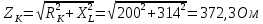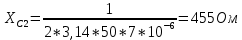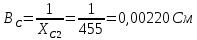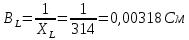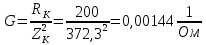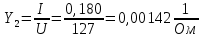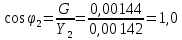






















Третий опыт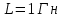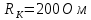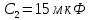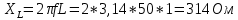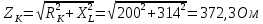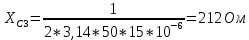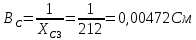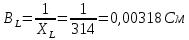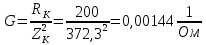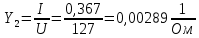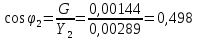

Режим	Результаты вычислений
	G	BC	BL	Y	cos φ
	См	См	См	См	-
1	0,00144	0,000628	0,00328	0,00215	0,669
2	0,00144	0,00220	0,00328	0,00142	1,0
3	0,00144	0,00472	0,00328	0,00289	0,498

Построим векторные диаграммы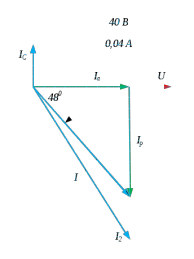


Рис 6 До резонансный режим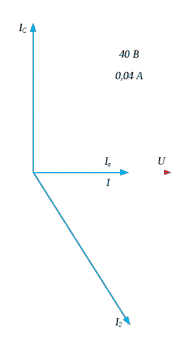


Рис 7 Резонанс токов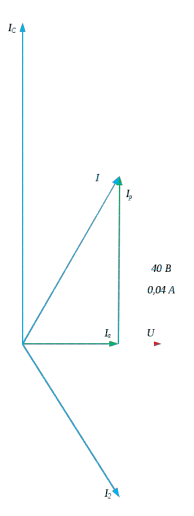



Рис 8 после резонансный режим

Выводы: при параллельном соединении индуктивности и ёмкости величина вектора тока в неразветвленной части цепи равна алгебраической сумме токов ветвей схемы. Резонанс токов в схеме наступит тогда, когда алгебраическая сумма вектора тока через катушку индуктивности будет равна вектору тока через ёмкость. При резонансе токов величина тока в неразветвленной части схемы будет самой минимальной.