ИССЛЕДОВАНИЕ ДИФФЕРЕНЦИРУЮЩИХ ЦЕПЕЙ. Исследование дифференцирующих и интегрирующих цепей
 Скачать 1.86 Mb.
|
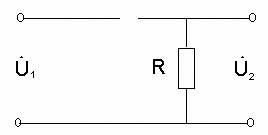
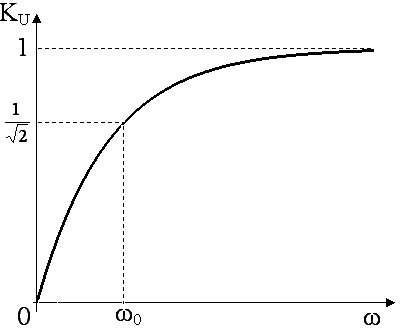
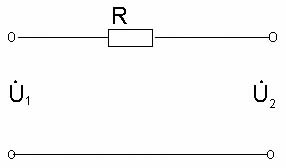
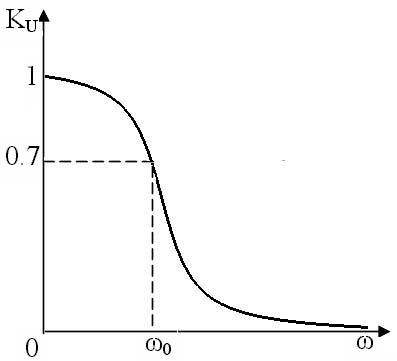
ИССЛЕДОВАНИЕ ДИФФЕРЕНЦИРУЮЩИХ И ИНТЕГРИРУЮЩИХ ЦЕПЕЙЦель работы изучение процессов прохождения гармонических сигналов, сигналов прямоугольной и треугольной формы через линейные пассивные и активные (дифференцирующую и интегрирующую) цепи. изучение переходных процессов в дифференцирующей и интегрирующей цепях; получение навыка работы с измерительными приборами (осциллограф и генератор сигналов различной формы); применение символического метода для расчета дифференцирующей и интегрирующей RC–цепей; обработка и анализ полученных экспериментальных данных. Задачи: измерить амплитудно-частотные характеристики пассивных и активных дифференцирующих и интегрирующих RC–цепей; измерить фазо-частотные характеристики выше перечисленных цепей; получить и исследовать переходные характеристики дифференцирующих и интегрирующих RC–цепей; экспериментально исследовать форму выходного напряжения при входном напряжении различной формы для цепей с различным значением постоянной τ:  ,  и  . 1 RC цепи В радиоэлектронике электрические цепи представляют собой совокупность соединенных схемных элементов, таких как резисторы, конденсаторы, катушки индуктивности, диоды, транзисторы, операционные усилители, источники тока, источники напряжения и другие. Соединяются схемные элементы с помощью проводов или печатных шин. Электрические цепи, составленные из идеализированных элементов, классифицируются по ряду признаков: - по энергетическим особенностям: активные (содержащие источники питания); пассивные цепи (не содержат источников тока и (или) напряжения); - по топологическим особенностям: планарные (плоские); непланарные; разветвленные; неразветвленные; простые (одно-, двухконтурные); сложные (многоконтурные, многоузловые); - по числу внешних выводов: двухполюсники; четырехполюсники; многополюсники; - от частоты измерительного поля: цепи с сосредоточенными параметрами (в цепях с сосредоточенными параметрами сопротивлением обладает только резистор, емкостью только конденсатор, индуктивностью только катушка индуктивности); цепи с распределенными параметрами (в цепях с распределенными параметрами даже соединительные провода обладают емкостью, проводимостью и индуктивностью, которые распределены вдоль их длины; наиболее характерен такой подход к цепям в области сверхвысоких частот); - от типа элементов: линейные цепи, если они состоят из линейных идеализированных элементов; нелинейные цепи, если в состав цепи входит хотя бы один нелинейный элемент; В данной работе рассмотрены пассивные цепи, состоящие из двух схемных элементов  и активные цепи содержащие операционный уселитель. Элементы  и  – называют идеализированными схемными элементами. Ток, протекающий через такие элементы, представляет собой линейную функцию от приложенного напряжения:для резистора :  ;для конденсатора :  ;Поэтому цепи, состоящие из  элементов, называются линейными. Строго говоря, на практике не все элементы линейны, но во многих случаях отклонения от линейности невелико и действительный элемент можно принимать как идеализированный линейный. Активное сопротивление можно рассматривать как линейный элемент только в том случае, если текущий через него ток настолько мал, что выделяющееся тепло не приводит к заметному изменению величины его сопротивления. Аналогичные соображения можно высказать в отношении конденсатора. Если параметры цепи остаются неизменными в течение времени, когда протекает изучаемый электрический процесс, то говорят о цепи с постоянными параметрами.Поскольку процессы в линейных цепях описываются линейными уравнениями, к ним применим принцип суперпозиции. Это значит, что результат действия в линейной цепи сигнала сложной формы можно найти как сумму результатов действий сигналов более простых, на которые разлагается исходный, сложный сигнал. Для анализа линейных цепей используется два метода: метод частотных характеристик и метод переходных характеристик. 2 Метод частотных характеристик 2.1 Основные понятия Линейные цепи обладают уникальным свойством: если на вход цепи подавать гармонический сигнал  ,то на выходе, независимо от типа линейной цепи, всегда будет тоже гармонический сигнал, отличающийся от входного амплитудой и фазой:  ,где 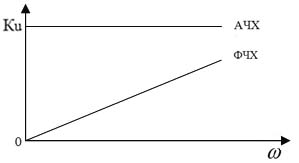 – комплексный коэффициент передачи линейной цепи.  , где  – модуль коэффициента передачи цепи. Он показывает, во сколько раз изменяется амплитуда сигнала после прохождения электрической цепи. Аргумент коэффициента передачи  показывает сдвиг по фазе выходного сигнала, прошедшего электрическую цепь, относительно входного. Сигнал, проходя через электрическую цепь, не искажается, если цепь имеет следующие идеализированные амплитудно-частотные (АЧХ) и фазочастотные (ФЧХ) характеристики:  Рисунок 1 – Амплитудно-частотная (АЧХ) и фазочастотная (ФЧХ) характеристики идеальной цепи, пропускающей сигналы без искажений То есть, условиями неискаженной передачи сигнала являются: постоянство модуля коэффициента передачи цепи во всем исследуемом диапазоне частот (  = const.) и линейная зависимость фазового сдвига от частоты ( ). Для реальной линейной цепи модуль коэффициента передачи зависит от частоты, а зависимость , как правило, нелинейная. Для каждой конкретной линейной цепи АЧХ и ФЧХ можно определить экспериментально или рассчитать теоретически. Рассмотрим простейшие линейные цепи и методы расчета модуля и аргумента комплексного коэффициента передачи этих цепей.2.2 Пассивная дифференцирующая RC цепь. Дифференцирующими называются четырехполюсники, напряжение на выходе которых пропорционально производной по времени от напряжения на входе, т.е. четырехполюсники, в которых выполняются условия  . (1)В качестве дифференцирующего элемента в таких цепях удобно использовать конденсатор, поскольку мгновенные значения напряжения и ток в нем связаны соотношением  . (2)Следовательно, если собрать цепь, в которой выходное напряжение 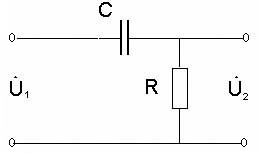 пропорционально току  , текущему через конденсатор, то она будет дифференцирующей. Чтобы выходное напряжение было пропорционально току, его следует снимать с резистора, включенного последовательно с конденсатором (рисунок 2).  Рисунок 2 – Схема дифференцирующей RC цепи В этом случае форма выходного напряжения повторяет форму тока в цепи. Но ток в цепи оказывается пропорциональным производной по времени не от входного напряжения, а от напряжения на конденсаторе (2)  . (3)Напряжения в цепи связаны соотношением:  . Откуда  . Тогда . (4)Если  , то . (5)Воспользуемся приближенным соотношением (5) и подставим его в (1): 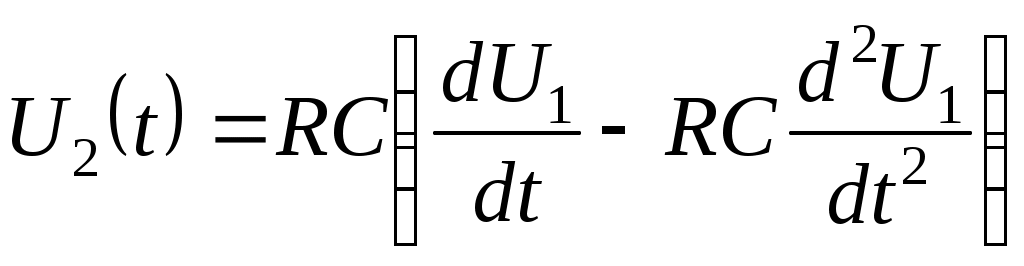 .Тогда, если  , то , (6)т.е. данная RC-цепь дифференцирует сигналы только при малых значениях  . Чем больше значения сопротивления и емкости конденсатора C, тем больше выходное напряжение  , и тем сильнее форма выходного напряжения отличается от производной входного напряжения по времени. Очевидно, что цепь, показанная на рисунке 1, близка к дифференцирующей при  , поскольку только в этом случае  .Рассмотрим прохождение гармонического сигнала через дифференцирующую цепь. Подадим на вход схемы (рисунок 2) гармонический сигнал  . На выходе сх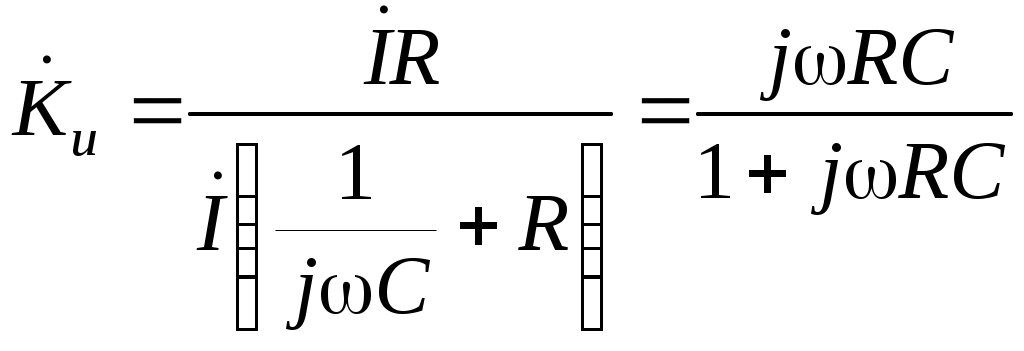емы появится сигнал  . Определим комплексный коэффициент передачи дифференцирующей цепи по формуле: .Напряжение представляет собой сумму падений напряжений на конденсаторе  и на резисторе  . Поэтому можно записать: , где  , Тогда  .Выделяя действительную и мнимую части 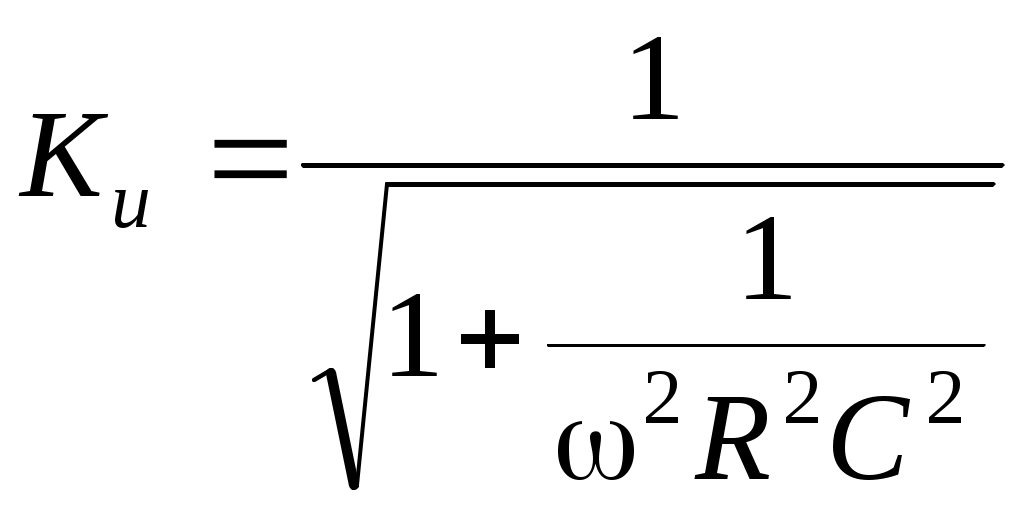 , запишем выражения для модуля коэффициента передачи и аргумента:   . (7)Видно, что модуль коэффициента передачи дифференцирующей цепи и аргумент зависят от частоты  . Проанализируем частотную зависимость модуля коэффициента передачи  :Пусть  , то есть колебания напряжения  практически отсутствуют, что соответствует постоянному току. В этом случае  , т.к. при стремлении частоты входного сигнала к нулю реактивное сопротивление конденсатора  . В эквивалентной схеме дифференцирующей цепи конденсатору C соответствует разрыв цепи (рисунок 3). При этом  , т.е. сигнал не проходит дифференцирующую цепь.В области высоких частот (при стремлении частоты входного сигнала к бесконечности) реактивное сопротивление конденсатора стремится к нулю и конденсатор в эквивалентной схеме дифференцирующей цепи можно заменить коротким замыканием (рисунок 4). При этом  , т.е. сигнал проходит цепь без искажений.
При частоте равной граничной частоте   . Принято считать, что в области частот, где  сигнал практически не искажается.Результаты анализа  позволяют изобразить качественно амплитудно-частотную характеристику (АЧХ) дифференцирующей цепи (рисунок 5).
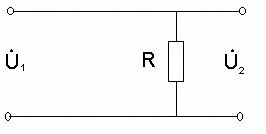
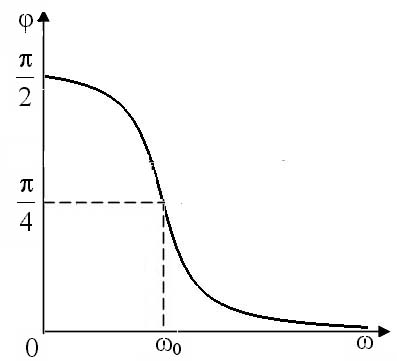
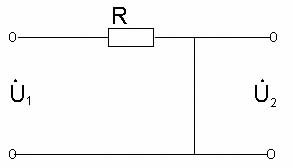
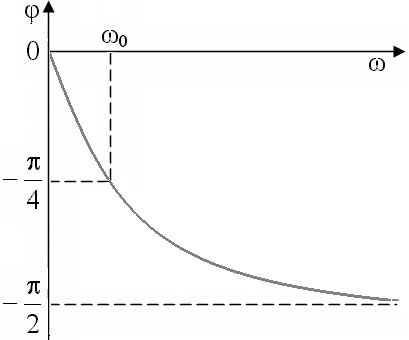
Проанализируем характер поведения аргумента комплексного коэффициента передачи от частоты, то есть зависимость сдвига фазы от частоты выходного сигнала, прошедшего дифференцирующую цепь, относительно входного. Согласно формуле (7)  :в области низких частот при стремлении к нулю  и  , то есть выходное напряжение опережает входное на четверть периода.в области высоких частот при   и  , то есть выходное и входное напряжения синфазны.при    tg=1 и =450, то есть выходное напряжение опережает входное на восьмую часть периода.Результаты анализа позволяют изобразить фазочастотную характеристику (ФЧХ) дифференцирующей цепи (рисунок 6). Частотные зависимости модуля коэффициента передачи и сдвига фаз иногда представляют в виде:  и  . А так как частоты и  связаны линейным соотношением  , то графики АЧХ и  имеют одинаковый вид, так же как ФЧХ  и  .Определим условие точного дифференцирования гармонического сигнала. Подадим на вход дифференцирующей цепи гармонический сигнал:  .Выходной сигнал будет равен ,или  .Обозначим  . U2m – амплитуда выходного сигнала. Тогда  .От сюда видно, что гармонический сигнал точно дифференцируется, если выходной сигнал опережает входной по фазе на  . Сложный периодический сигнал можно представить в виде гармоник с различными амплитудами и частотами кратными основной частоте. Чтобы выполнялось условие точного дифференцирования сложного сигнала, необходимо, чтобы для любой гармоники выходного напряжения опережало ее входное напряжение на  . Но  . На практике можно брать  . С другой стороны  . Но  , следовательно,  . Тогда  откуда следует  т.е. точное дифференцирование сигналов происходит в очень узкой области частот на низких частотах, где коэффициент передачи дифференциальной цепи очень мал (рисунок 5).Таким образом, дифференцирующая цепь точно дифференцирует сигналы только при коэффициенте передачи, близком к 0. По мере увеличения величины C коэффициент передачи возрастает, а форма выходного напряжения  все больше становится отличной от значений  , все, более приближаясь к форме входного напряжения  . При  цепь из дифференцирующей превращается в разделительную, фаза при этом стремится к 0 (рисунок 6).Таким образом, дифференцирующими являются цепи, в которых  или  , где  – постоянная времени цепи,  – период (для периодических) или длительность (для непериодических) сигналов. Несмотря на то, что получить идеальное дифференцирование не представляется возможным, дифференцирующие цепи, собранные на пассивных -элементах широко используются на практике. Подобные цепи применяют чаще всего для получения узких коротких импульсов с крутыми фронтами, а вовсе не для математического дифференцирования. Частотой, при которой цепь еще не искажает сигнала, считают граничную частоту цепи равную  . Оценим диапазон частот, в котором выполняется условие точного дифференцирования сигнала.2.3 Активная дифференцирующая RC цепь. Малый коэффициент передачи является серьезным недостатком пассивной дифференцирующей цепи. От этого недостатка свободна активная дифференцирующая цепь. Как известно, в цепи на рисунке 7 а комплексный коэффициент передачи операционного усилителя 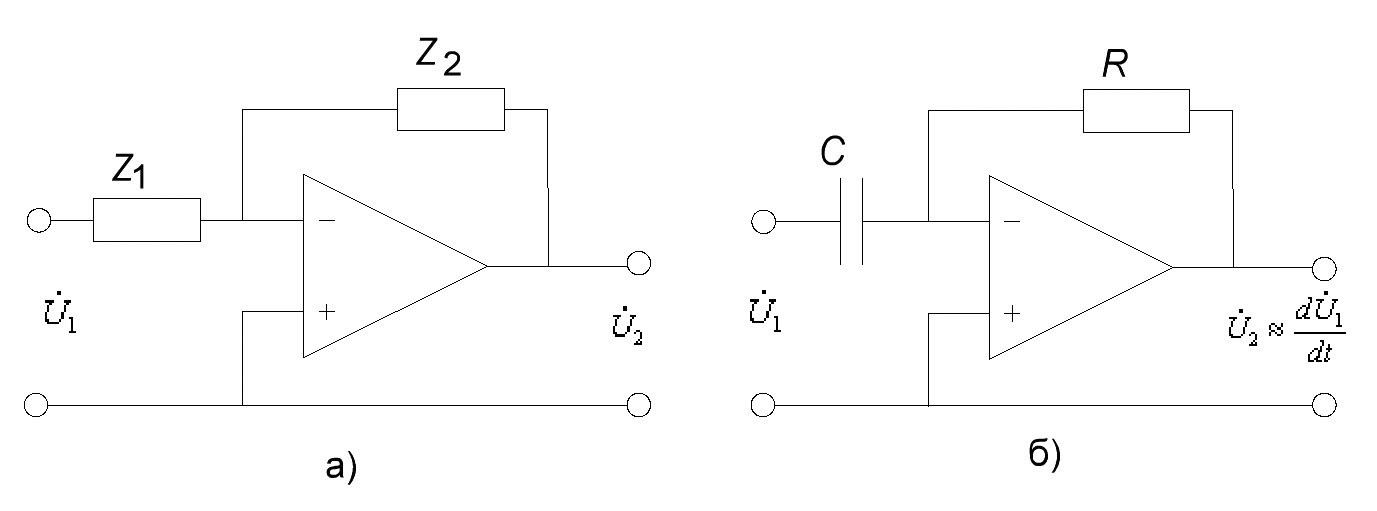 . Если в качестве элемента  включить конденсатор емкостью , а в качестве элемента  – резистор сопротивлением , то схема приобретает вид, показанный на рисунке 7 б.  Рисунок 7 – Активные цепи Комплексный коэффициент передачи для этого случая имеет вид 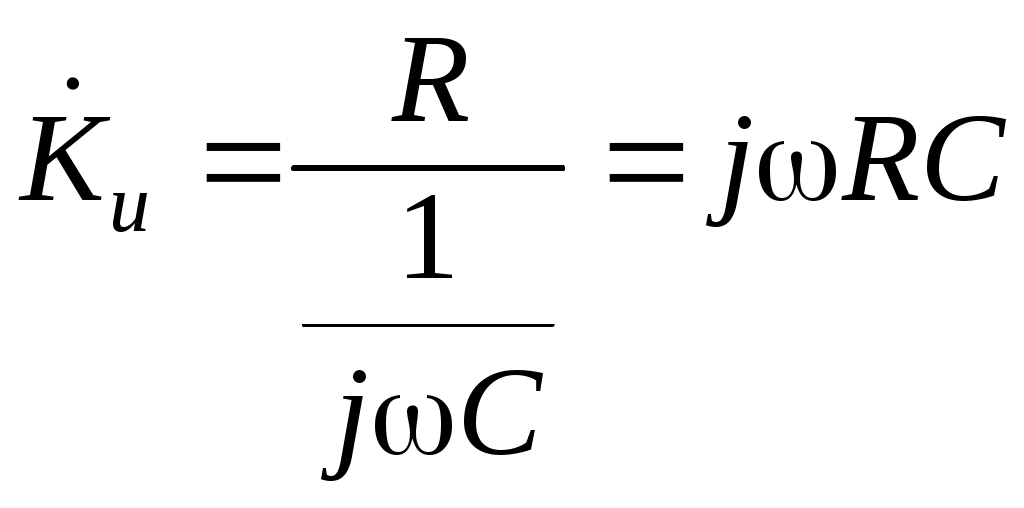 .Но всякая цепь, коэффициент передачи которой пропорционален частоте, представляет дифференцирующую цепь. Если в пассивной дифференцирующей цепи коэффициент передачи много меньше единицы, то в активной цепи он может быть либо близким к единице, либо даже больше единицы при одинаковом качестве дифференцирования. 2.4 Пассивная интегрирующая RC цепь Интегрирующими называются четырехполюсники, напряжение на выходе которых пропорционально интегралу от напряжения на входе, т.е. четырехполюсники, в которых выполняется условие  .Интегрирующие цепи могут быть либо пассивными, либо активными. Покажем, что цепь на рисунке 8, в которой 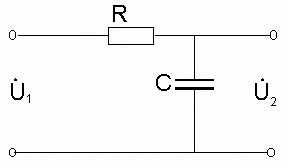 является практически интегрирующей.  Рисунок 8 – Схема интегрирующей RC цепи Если  , то  . В этом случае  . Тогда .Таким образом, цепь на рисунке 8 будет практически интегрирующей, если коэффициент передачи данной цепи много меньше 1 или постоянная времени цепи  много больше периода входного напряжения Т.Проводя для интегрирующей цепи, такие же рассуждения, как и для дифференцирующей цепи, запишем  , где  .То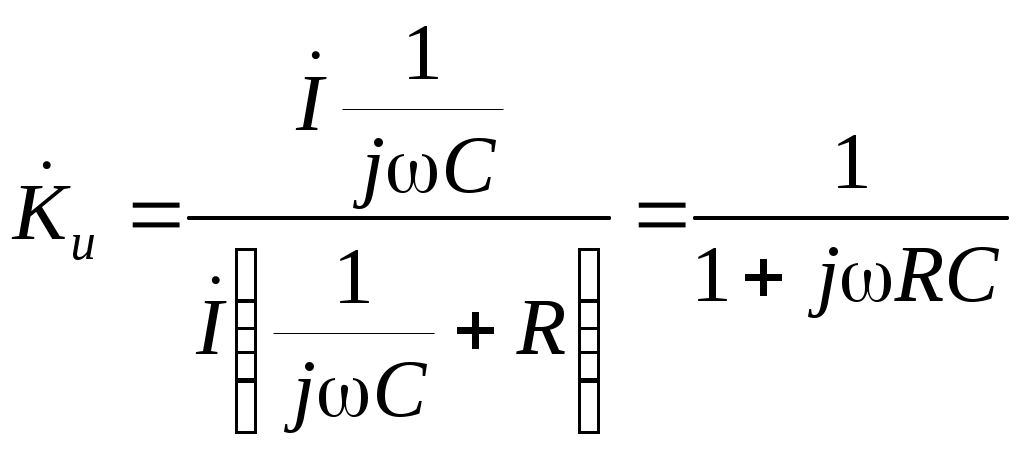гда  , т.е. комплексный коэффициент передачи интегрирующей цепи зависит от частоты  . Определим модуль и аргумент коэффициента передачи и  .Проведём анализ частотной зависимости . При стремлении частоты входного сигнала к нулю сопротивление конденсатора стремится к бесконечности, поэтому на месте конденсатора в схеме интегрирующей цепи получается разрыв (рисунок 9); На высоких частотах, при стремлении частоты входного сигнала к бесконечности, сопротивление конденсатора стремится к нулю и в эквивалентной схеме конденсатор можно заменить коротким замыканием (рисунок 10). При   .
По результатам анализа зависимости интегрирующей цепи, можно построить амплитудно-частотную характеристику (рисунок 11). Тангенс разности фаз между сигналом на выходе и на входе равен , откуда можно получить фазочастотную зависимость интегрирующей цепи: . Проанализируем эту зависимость:При стремлении к нулю  стремится к нулю и  , то есть выходное и входное напряжения синфазны..При стремлении к бесконечности  стремится к минус бесконечности и стремится к минус 900, то есть выходное напряжение отстает входное на четверть периода.При  ,  и  , то есть выходное напряжение отстает входное на восьмую часть периода.Фазочастотная характеристика данной интегрирующей цепи изображена на рисунок 12.
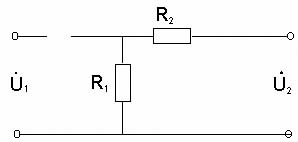
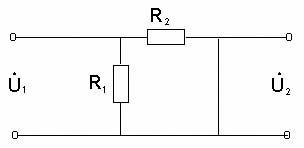
Определим условие точного интегрирования гармонического сигнала. Подадим на вход интегрирующей цепи гармонический сигнал: ,то выходной сигнал будет равен ,или  .Обозначим – амплитуда выходного сигнала. Тогда  .От сюда видно, что условием точного интегрирующей сигнала является отставание выходного сигнала по фазе на относительно входного.Чтобы выполнялось условие точного интегрирования сложного сигнала, необходимо, чтобы для любой гармоники выходного напряжения отставало ее входное напряжение на  . Но  . Проводя аналогичные рассуждения как для точного дифференцирования можно получить следующее соотношение  т.е. точное интегрирование сигналов происходит в очень узкой области частот на высоких частотах, где коэффициент передачи дифференциальной цепи очень мал (рисунок 11).Таким образом, интегрирующая цепь точно интегрирует сигналы только при коэффициенте передачи, близком к 0. По мере уменьшения величины C коэффициент передачи возрастает, а форма выходного напряжения все больше становится отличной от значений , все, более приближаясь к форме входного напряжения . При цепь из интегрирующей превращается в разделительную, фаза при этом стремится к 0 (рисунок 12).Таким образом, интегрирующими являются цепи, в которых или . Несмотря на то, что получить идеальное интегрирования не представляется возможным, интегрирующие цепи, собранные на пассивных -элементах широко используются на практике. Частотой, при которой цепь еще не искажает сигнала, считают граничную частоту цепи равную . Оценим диапазон частот, в котором выполняется условие точного дифференцирования сигнала.2.5 Активная интегрирующая RC цепь Активную интегрирующую цепь собирают по схеме, показанной на рисунке 13. 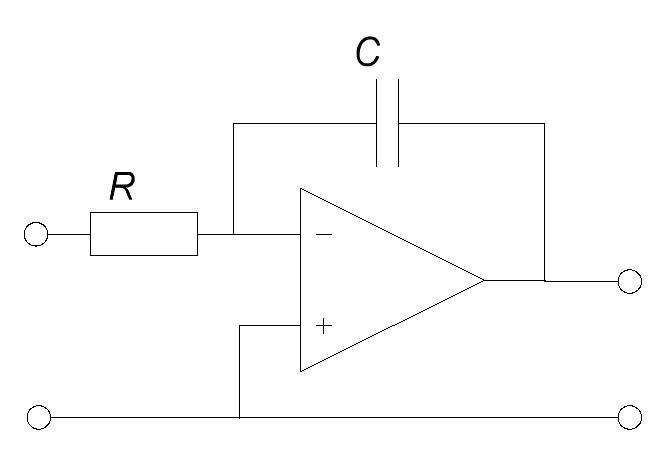 Рисунок 13 – Активная интегрирующая цепь В данной цепи  , т.е.  , и, следовательно, цепь является интегрирующей.2.5 Дифференцирующе–интегрирующая цепь Цепь, которая состоит из соединенных последовательно дифференцирующей и интегрирующей цепей, называют дифференцирующее–интегрирующей цепью. Воспользуемся рассуждениями, изложенными выше, для дифференцирующей и интегрирующей цепей и получим комплексный коэффициент передачи дифференцирующее–интегрирующей цепи. Если напряжение на конденсаторе 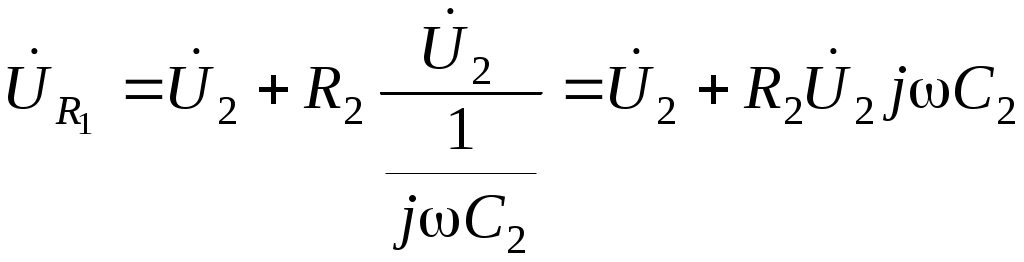 равно  , то напряжение на резисторе  равно Воспользовавшись уравнениями Кирхгофа, выразим через : Проведем математические преобразования последнего выражения с учетом того, что 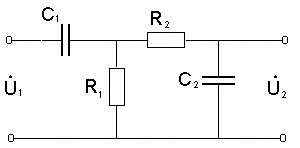 и  :   . Рисунок 14 – Схема последовательно соединённых дифференцирующей и интегрирующей цепей. 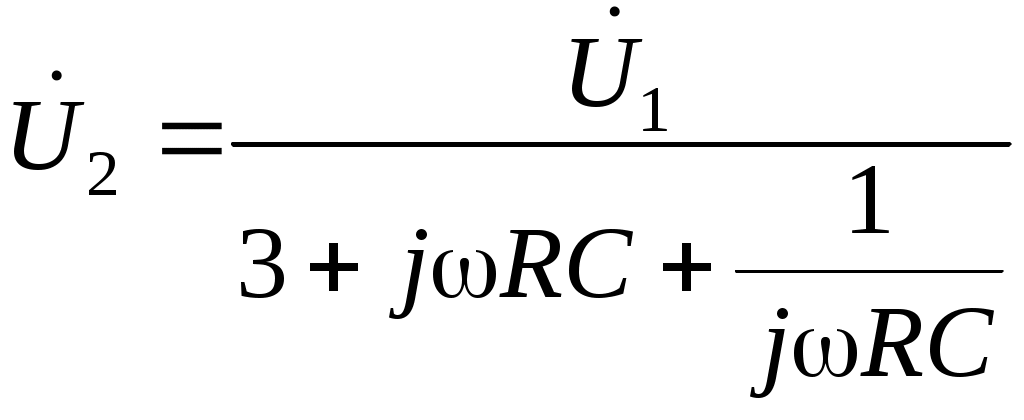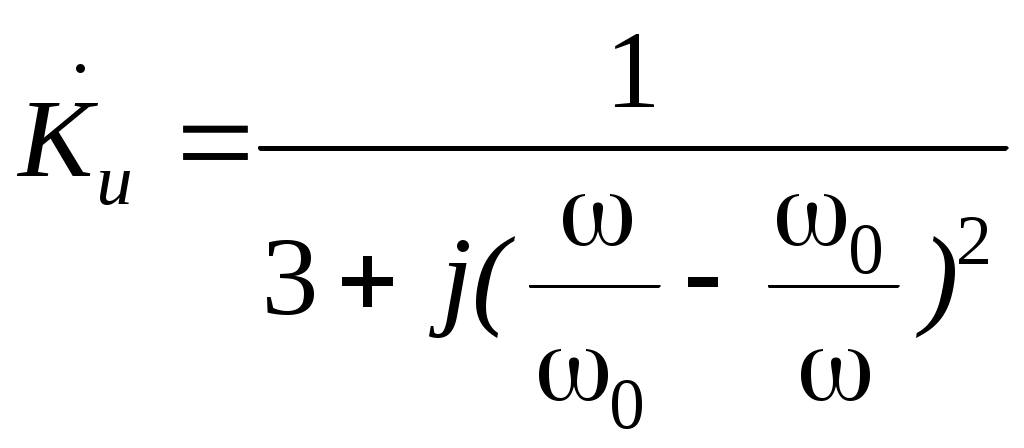Определим выходное напряжение:  или, обозначив граничную частоту  , получим окончательно выражение для комплексного коэффициента дифференцирующее–интегрирующей цепи: .Найдем модуль коэффициента передачи этой цепи: 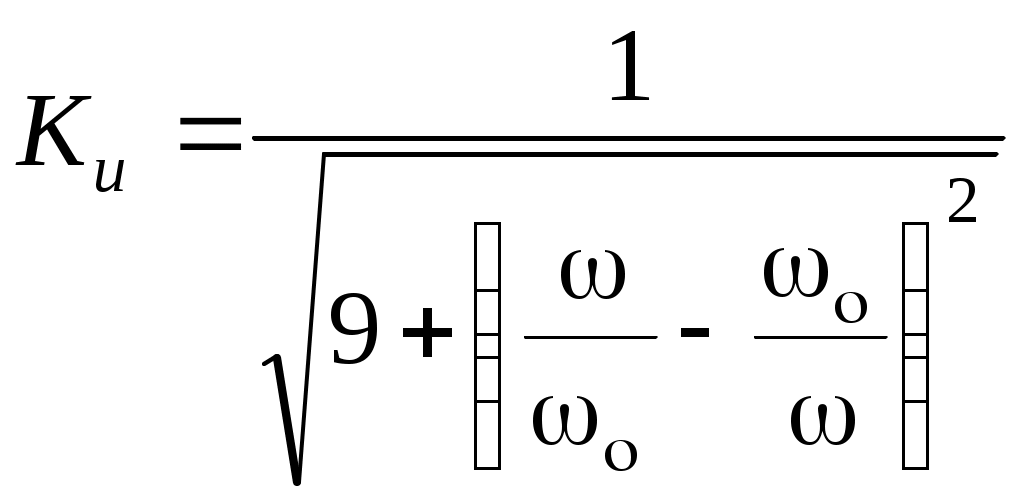 .Проанализируем полученную частотную зависимость : при  при  при  .При стремлении частоты к нулю или к бесконечности в схеме дифференцирующее–интегрирующей цепи конденсаторы можно заменить разрывом (рисунок 15) и коротким замыканием (рисунок 16), соответственно.
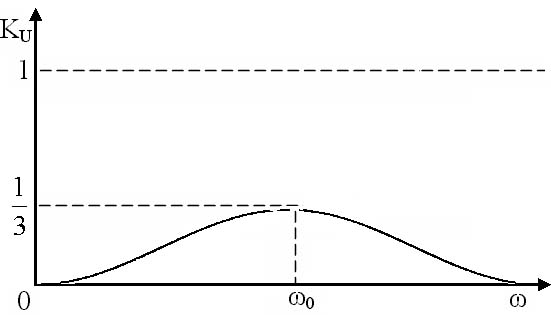
График амплитудно-частотной характеристики дифференцирующее–интегрирующей цепи имеет вид размытой резонансной кривой с максимумом на частоте ω0, называемой квазирезонансной частотой (рисунок 17). Выразим аргумент комплексного коэффициента дифференцирующее–интегрирующей цепи:  .Проанализируем полученную частотную зависимость φ(ω): при  ;при  ;при  .
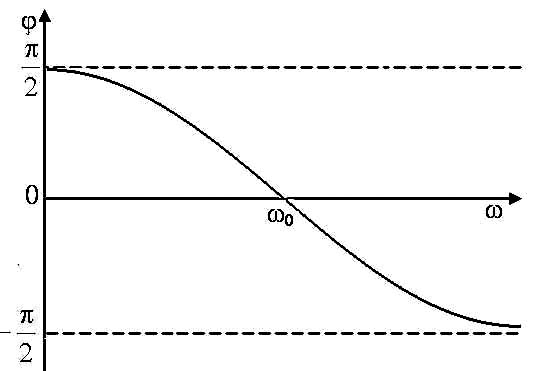
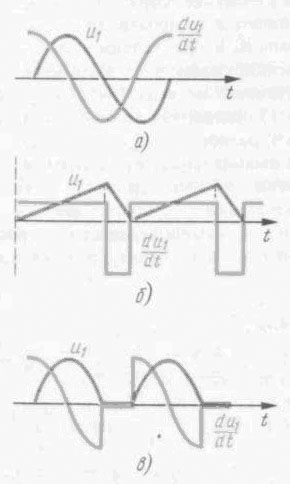
Результаты анализа позволяют построить фазочастотную характеристику дифференцирующее–интегрирующей цепи (рисунок 18). 3 Метод переходных характеристик Прохождение НЕГАРМОНИЧЕСКИХ СИГНАЛОВ через ПАСИВНЫЕ И АКТИВНЫЕ RC-цепи Кроме частного подхода в радиоэлектронике широко используется временной подход. В этом случае электрическая цепь характеризуется переходной функцией или переходной характеристикой. Переходная характеристика – это отклик цепи, то есть – это напряжение на выходе цепи при подаче на её вход единичного скачка напряжения. В хорошо разработанном анализе цепей методом переходных характеристик в качестве элементарного сигнала выбирают мгновенный скачок напряжения, т.е. напряжение, претерпевающее в фиксированный момент времени изменение на некоторую величину  ,которая может быть принята равной единице. Такой сигнал носит название единичного скачка напряжения. Зависимость от времени выходного напряжения, отнесенного к величине скачка входного напряжения  , носит название переходной характеристики цепи. Очевидно, что по самому ее смыслу переходная характеристика определяет искажения сигналов, проходящих через линейные цепи.При скачке напряжения, приложенного к цепи состоящей из последовательно включенных R и C элементов, в первый момент времени конденсатор C не заряжен и всё напряжение приложено к резистору R. Затем конденсатор начинает заряжаться, а напряжение на резисторе уменьшается. Найдем, по какому закону изменяются напряжения на C и R. Так как токи, протекающие через резистор и конденсатор одинаковые ( IR=IC ), то  или  . Полученное дифферинцеальное уравнение имеет решение:  . Константа A определяется из начальных условий: при t = 0 UC = 0. Следовательно, A = -U1. Тогда  Так как входное напряжение U2 равно сумме напряжений на конденсаторе и резисторе, то  Таким образом, при подаче на последовательную RC цепь скачка напряжения на конденсаторе напряжение растет, а на резисторе - уменьшается по экспоненциальному закону. 3.1 Дифференцирующая цепь Для определения формы сигнала на выходе дифференцирующей цепи необходимо графически построить производную по времени от входного напряжения. Напомним, что производная представляет величину, пропорциональную тангенсу угла наклона между касательной, проведенной в данной точке, и осью времени. Примеры кривых входного и выходного напряжений показаны на рисунке 19. Если напряжение на входе дифференцирующей цепи нарастает скачкообразно, то ток в  -цепи, а следовательно, и выходное напряжение  нарастают также скачкообразно. Но при скачкообразном уменьшении напряжения конденсатор разряжается по экспоненциальному закону, причем, чем больше постоянная времени цепи, тем медленнее разряжается конденсатор и тем кривая на выходе сильнее отличается от производной. Например, при напряжении прямоугольной формы на входе, напряжения на выходе имеют вид показанный на рисуноке 20.
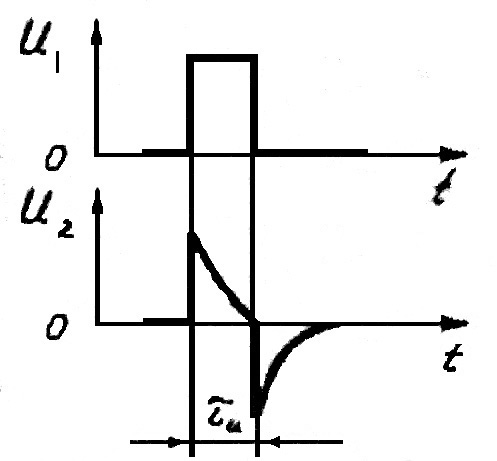
В момент времени  подадим на вход дифференцирующей цепи, представляющей собой делитель напряжения на конденсаторе и резисторе, единичный. прямоугольный импульс. Прямоугольный импульс представляет собою кратковременный сигнал, где напряжение изменяется скачком дважды: при t1 мгновенно нарастает, а при t2 так же быстро убывает.Как и при единичном скачке входного напряжения, в начальный момент конденсатор не заряжен и напряжение полностью приложено к резистору. Затем конденсатор начинает заряжаться и напряжение на нем растет по экспоненте , а напряжение на резисторе уменьшается так же по экспоненциальному закону. В момент времени  , когда импульс закончился, конденсатор оказался заряженным. При  конденсатор разряжается через источник питания. По резистору течет ток разряда в направлении противоположном току заряда и на выходе дифференцирующей цепи появляется отрицательное напряжение, т.е. возникает импульс отрицательной полярности (рисунок 21).
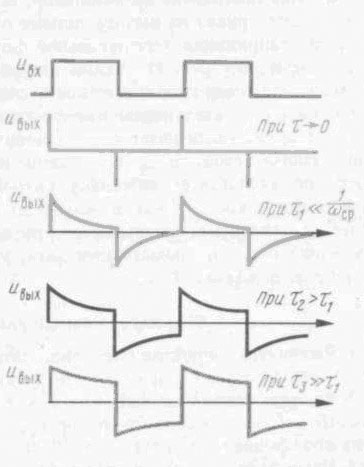
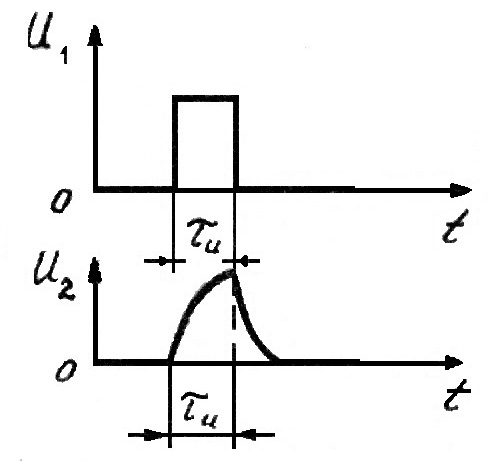
Таким образом, прямоугольный импульс, приложенный ко входу дифференцирующей цепи преобразуется в два импульса: один положительной, а другой отрицательной полярности. Если дифференцирующая цепь нагружена на емкость, например входную емкость следующего каскада (рис. 7), 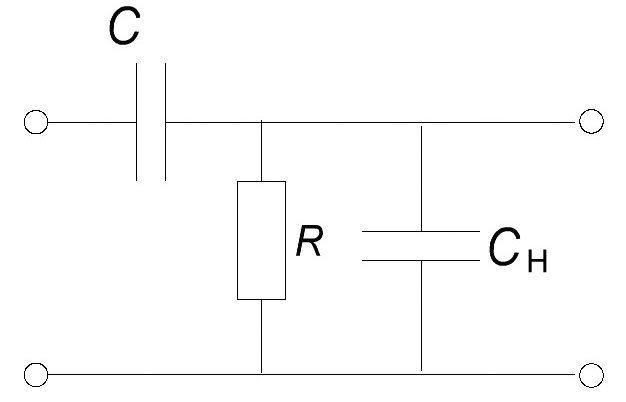 Рис. 7 то это приводит к следующим изменениям: 1) постоянная времени эквивалентной цепи увеличивается и становится равной  ; 2) вследствие наличия емкости  , напряжение на выходе нарастает не скачком, а также по экспоненте, поскольку напряжение на емкости не может изменяться скачкообразно. В результате верхушки импульсов получаются более скругленными, уменьшается крутизна нарастания переднего фронта, увеличивается длительность импульса, уменьшается амплитуда выходного напряжения (рис. 8). 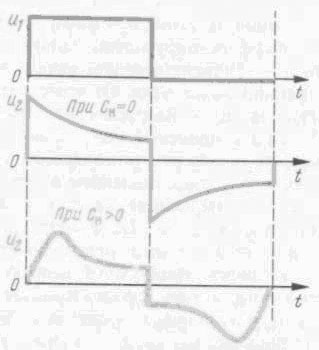 Рис. 8 Интегрирующие цепи используют для получения на выходе сигналов, длительность которых больше, чем у входных, а крутизна фронтов меньше. Такие цепи выполняют разнообразные функции, например, позволяют уменьшить воздействие импульсных помех, преобразуют сигналы, отличающиеся по длительности, в сигналы, отличающиеся по амплитуде и т.д. При воздействии коротких импульсов конденсатор не успевает полностью зарядиться, а при воздействии длительного – успевает, за счет чего возникает разница в напряжениях на выходе цепи (рисунок 12). 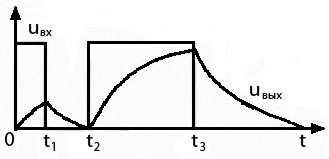 Рисунок 12 – Переходные процессы в интегрирующей цепи Напряжение на выходе интегрирующей цепи будет такой формы, при которой производная от выходного напряжения повторяет форму напряжения на входе. Например, если входное напряжение имеет прямоугольную форму, то напряжение на выходе цепи – треугольную, поскольку производная от треугольной кривой имеет прямоугольную форму. Длительность импульсов выходного напряжения  в интегрирующих цепях больше длительности входного напряжения  . |
.
.
.
.
