Лабораторная Механические калебании. Солосенков А.С.. Исследование движения тела под действием квазиупругой силы
 Скачать 165.94 Kb. Скачать 165.94 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ ЦЕЛЬ РАБОТЫ: Выбор физических моделей для анализа движения тел. Исследование движения тела под действием квазиупругой силы. Экспериментальное определение зависимости частоты колебаний от параметров системы. КРАТКАЯ ТЕОРИЯ: КОЛЕБАНИЕ – периодически повторяющееся движения тела. ПЕРИОД T – минимальное время, через которое движение полностью повторяется.  ГАРМОНИЧЕСКОЕ КОЛЕБАНИЕ – движение, при котором координата тела меняется со временем по закону синуса или косинуса: ГАРМОНИЧЕСКОЕ КОЛЕБАНИЕ – движение, при котором координата тела меняется со временем по закону синуса или косинуса: 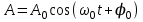 . .Основными характеристиками гармонических колебаний являются: АМПЛИТУДА А0 – максимальное значение параметра А. ЦИКЛИЧЕСКАЯ ЧАСТОТА собственных колебаний ω0 – в 2π раз большая обычной или линейной частоты ν = 1/Т (ν – число полных колебаний за единицу времени). ФАЗА (ω0t + ϕ0) – значение аргумента косинуса. НАЧАЛЬНАЯ ФАЗА ϕ0 – значение аргумента косинуса при t = 0.  ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ свободных гармонических колебаний параметра А: ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ свободных гармонических колебаний параметра А: 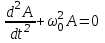 , свободных затухающих колебаний: , свободных затухающих колебаний:  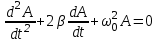 , где β – коэффициент затухания. , где β – коэффициент затухания.МАТЕМАТИЧЕСКИЙ МАЯТНИК (ММ) – это МОДЕЛЬ объектов, в которых могут происходить гармонические колебания. ММ – это материальная точка, подвешенная на идеальной (невесомой и нерастяжимой) нити. Формулы для ω0 в этих системах выпишите из конспекта или учебника. 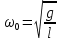 - циклическая частота для ММ - циклическая частота для ММ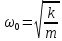 – собственная частота для свободных затухающих колебаний – собственная частота для свободных затухающих колебаний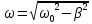 - частота затухающих колебаний - частота затухающих колебанийЗАДАНИЕ: Выведите формулу для циклической частоты свободных колебаний математического маятника. Дифференциальное уравнение второго порядка 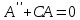 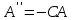 Дифференциальное уравнение второго порядка гармонических колебаний 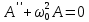 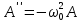 Решение этого уравнения: А= 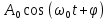 C= 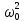 Для математического маятника 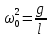 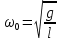 МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ Внимательно рассмотрите рисунки, найдите все регуляторы и другие основные элементы. Зарисуйте поле движения тела с регуляторами соответствующих параметров (укажите, что они регулируют).  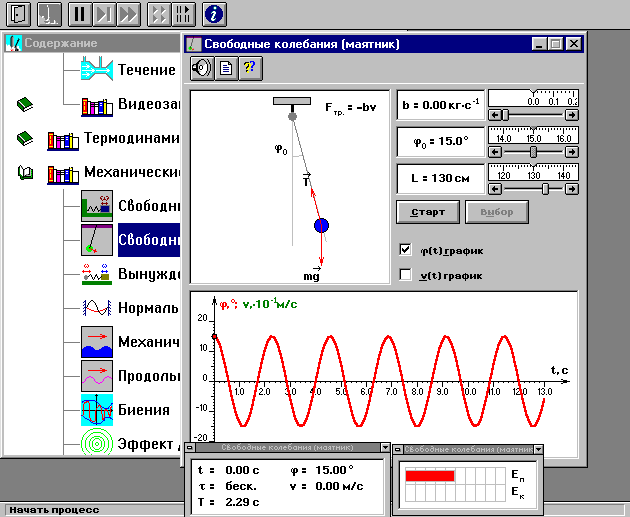 ЭКСПЕРИМЕНТ Выберите «Маятник». Установите с помощью движков регуляторов максимальную длину нити L и значения коэффициента затухания и начального угла, указанные в табл. 1 для вашей бригады. Нажимая мышью на кнопку «СТАРТ», следите за движением точки на графиках угла и скорости и за поведением маятника. Потренируйтесь, останавливая движение кнопкой «СТОП» (например, в максимуме смещения) и запуская далее кнопкой «СТАРТ». Выберите число полных колебаний N =3–5 и измеряйте их продолжительность Δt (как разность t2 – t1 из таблицы на экране). Приступайте к измерениям длительности Δt для N (3-5) полных колебаний, начиная с максимальной длины (150 см) нити маятника и уменьшая ее каждый раз на 10 см (до минимальной длины 80 см). Длину нити L и результаты измерений длительности Δt записывайте в табл. 2, образец которой приведен ниже. Таблица 1. Значения коэффициента затухания (вязкого трения), начального угла отклонения .
Таблица 2. Результаты измерений (количество измерений и строк – 8)
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА: Заполните таблицу 2 значениями Т вашего варианта (смотри прилагаемую инструкцию). Вычислите требуемые величины (Т2,с2 ) . Постройте графики зависимости: квадрата периода колебаний от длины нити ММ.  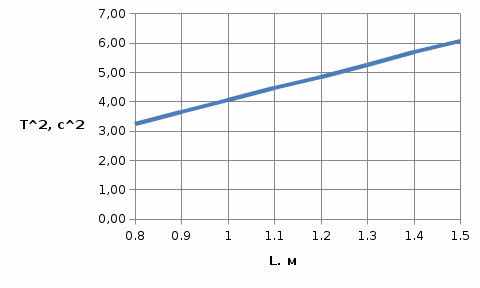 По наклону графика Т2 = f(L) определите значение g, используя формулу g =4π2 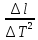 . . g=4 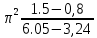 = 9,83 (м/с^2) = 9,83 (м/с^2)Оцените абсолютную ошибку определения g. Проанализируйте ответ и графики. График – прямая зависимость квадрата периода от длины нити маятника. Значение приближено к табличному g=9.81 м/с^2 Вопросы и задания для самоконтроля Что такое колебание? Колебания — это движение, повторяющееся через определённые интервалы времени, при котором тело поочерёдно отклоняется то в одну, то в другую сторону от положения равновесия. Дайте определение периода колебаний. Период колебаний — это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно. Дайте определение частоты колебаний. Частота колебаний – это число колебаний за единицу времени. Дайте определение гармонических колебаний. Гармонические колебания — это такие колебательные движения, при которых смещение тела от положения равновесия совершается по закону синуса или косинуса. Запишите закон зависимости от времени характеристики А, совершающей гармоническое колебательное изменение. 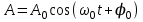 Запишите закон движения ММ, совершающей гармонические колебания. x(t)= 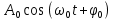 Дайте определение амплитуды гармонических колебаний. АМПЛИТУДА А0 – максимальное значение параметра А. Дайте определение фазы гармонических колебаний. ФАЗА (0t + 0) – значение аргумента косинуса. Дайте определение начальной фазы гармонических колебаний. НАЧАЛЬНАЯ ФАЗА 0 – значение аргумента косинуса при t = 0. Напишите уравнение связи частоты и периода гармонических колебаний. = 1/Т Напишите уравнение связи частоты и циклической частоты гармонических колебаний. 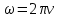 Напишите формулу зависимости скорости ММ от времени при гармонических колебаниях. 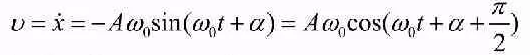 Напишите уравнения связи амплитуды скорости и амплитуды смещения при гармонических колебаниях ММ.  Напишите формулу зависимости ускорения ММ от времени при гармонических колебаниях. 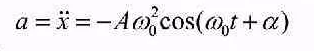 Напишите уравнения связи амплитуды скорости и амплитуды ускорения при гармонических колебаниях ММ. 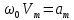 Напишите уравнения связи амплитуды смещения и амплитуды ускорения при гармонических колебаниях ММ. Напишите дифференциальное уравнение свободных гармонических колебаний ММ. 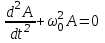 Напишите дифференциальное уравнение свободных затухающих колебаний ММ. 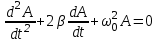 , где – коэффициент затухания. , где – коэффициент затухания.Что определяет коэффициент затухания? Коэффициент затухания определяет скорость уменьшения амплитуды колебаний: он обратен по величине промежутку времени, за который амплитуда уменьшается в e раз. Дайте определение математического маятника. МАТЕМАТИЧЕСКИЙ МАЯТНИК (ММ) – это МОДЕЛЬ объектов, в которых могут происходить гармонические колебания. ММ – это материальная точка, подвешенная на идеальной (невесомой и нерастяжимой) нити. Запишите формулу циклической частоты свободных колебаний математического маятника.  Дайте определение пружинного маятника. Пружи́нный ма́ятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m. Запишите формулу циклической частоты свободных колебаний пружинного маятника. 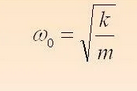 Какие процессы происходят при вынужденных колебаниях? Вынужденные колебания — колебания, происходящие под воздействием внешних периодических сил. Что такое резонанс? Резона́нс — частотно-избирательный отклик колебательной системы на периодическое внешнее воздействие, который проявляется в резком увеличении амплитуды стационарных колебаний При каком затухании резонанс будет более резким? При низком (но не незначительном) затухании резонанс представляет собой резкий максимум, который почти точно соответствует собственной угловой частоте. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
