Иследование метода Хаффмана. КР_ТИС_Никитин1. Исследование эффективного кодирования. Метод Хаффмана

• Название: Исследование эффективного кодирования. Метод Хаффмана
• Анкор: Иследование метода Хаффмана
• Дата: 28.05.2020
• Размер: 0.96 Mb.
• Имя файла: КР_ТИС_Никитин1.docx
• Тип: Исследование; #126302

Министерство науки и высшего образования Российской Федерации
ФГБОУ ВО «Кубанский государственный технологический университет»

(ФГБОУ ВО «КубГТУ»)

Институт компьютерных систем и информационной безопасности

Кафедра информационных систем и программирования

Направление подготовки 09.03.04 Программная инженерия

Профиль беспрофильный
КУРСОВАЯ РАБОТА
по дисциплине Теория информации и сигналов

на тему: «Исследование эффективного кодирования. Метод Хаффмана»

Выполнил студент 2 курса группы 18-КБ-ПР1 В. А. Никитин
Д опущен к защите ____________

Руководитель (нормоконтролер) работы ст. преп. Н.В. Кушнир

Защищена

____________

Оценка

____________

Члены комиссии: канд.тех.наук, ст. преп.К.Е. Тотухов

ст. преп. Ю.С. Носова

Краснодар

2020 г.

ФГБОУ ВО «Кубанский государственный технологический университет»

(ФГБОУ ВО «КубГТУ»)

Институт компьютерных систем и информационной безопасности

Кафедра информационных систем и программирования

Направление подготовки 09.03.04 Программная инженерия

Профиль беспрофильный
УТВЕРЖДАЮ

З аведующая кафедрой ИСП
М.В. Янаева

«11» февраля 2020 г.

ЗАДАНИЕ

на курсовую работу
Студенту В. Никитину 2 курса группы 18-КБ-ПР1

Тема работы: «Исследование эффективного кодирования. Метод Хаффмана»

(утверждена указанием директора института №24/19-КТ от «11» февраля 2020 г.)

План работы:

1. Анализ предметной области

2. Алгоритм исследования критерия идеального наблюдателя

3. Программная реализация
Объем работы:

а) пояснительная записка 21 с.

б) иллюстрированная часть 0 листов
Рекомендуемая литература:

1. Ключко В.И., Власенко А.В., Кушнир Н.В., Кушнир А.В. Теория информации и сигналов: учеб. пособие / Кубан. гос. технол. ун-т. Краснодар: Изд. ФГБОУ ВПО «КубГТУ», 2014.-132 с.
Срок выполнения работы: с «11» февраля по «__» мая 2020 г.

Срок защиты: «__» мая 2020 г.

Дата выдачи задания: «11» февраля 2020 г.

Дата сдачи работы на кафедру: «__» мая 2020 г.




Руководитель работы ст. преп. Н.В. Кушнир




Задание принял студент «11» февраля 2020 г. _________ В. А. Никитин




Реферат

Пояснительная записка курсовой работы 26 с., 9 рис., 5 источников.
РАЗРАБОТКА ПО, КОДИРОВАНИЕ, КОД ХАФФМАНА, АРХИВАТОР, СЖАТИЕ, ДАННЫЕ.

Объектом исследования является кодирование методом Хаффмана с применением языка C# и применение принципов объектно-ориентированного программирования.

Цель работы состоит в разработке программы на языке C#, демонстрирующей эффективное кодирование Хаффмана, с помощью среды разработки MicrosoftVisualStudio 2019 в режиме WindowsForms.

К полученным результатам относится отлаженная программа в Microsoft Visual Studio на языке программирования C#.

Содержание

Введение 5

1 Нормативные ссылки 7

2 Анализ предметной области 8

3 Реализация 12

3.1 Среда разработки и организация решения 12

3.3 Реализация алгоритма Хаффмана 12

3.2 Описание программы 17

Список используемой литературы 20

Приложение А – Скриншот проверки курсовой работы в системе Antiplagiat.ru3 21

Приложение Б – Листинг программы «Реализация кода Хаффмана в архиваторе» 22

Приложение В – Результаты работы программы «Реализация кода Хаффмана в архиваторе» 26

Введение

Сжатие информации - проблема, имеющая достаточно давнюю историю, гораздо более давнюю, нежели история развития вычислительной техники, которая (история) обычно шла параллельно с историей развития проблемы кодирования и шифровки информации.

Все алгоритмы сжатия оперируют входным потоком информации, минимальной единицей которой является бит, а максимальной - несколько бит, байт или несколько байт.

Целью процесса сжатия, как правило, есть получение более компактного выходного потока информационных единиц из некоторого изначально некомпактного входного потока при помощи некоторого их преобразования.

Основными техническими характеристиками процессов сжатия и результатов их работы являются:

- степень сжатия (compress rating) или отношение (ratio) объемов исходного и результирующего потоков;

- скорость сжатия - время, затрачиваемое на сжатие некоторого объема информации входного потока, до получения из него эквивалентного выходного потока;

- качество сжатия - величина, показывающая на сколько сильно упакован выходной поток, при помощи применения к нему повторного сжатия по этому же или иному алгоритму.

Кодирование Хаффмана является простым алгоритмом для построения кодов переменной длины, имеющих минимальную среднюю длину. Этот весьма популярный алгоритм служит основой многих компьютерных программ сжатия текстовой и графической информации. Некоторые из них используют непосредственно алгоритм Хаффмана, а другие берут его в качестве одной из ступеней многоуровневого процесса сжатия. Метод Хаффмана производит идеальное сжатие (то есть, сжимает данные до их энтропии), если вероятности символов точно равны отрицательным степеням числа 2. Алгоритм начинает строить кодовое дерево снизу вверх, затем скользит вниз по дереву, чтобы построить каждый индивидуальный код справа налево (от самого младшего бита к самому старшему). Начиная с работ Д.Хаффмана 1952 года, этот алгоритм являлся предметом многих исследований

1 Нормативные ссылки

ГОСТ 2.105-95 Общие требования к текстовым документам

ГОСТ 7.32-2001 СИБИД. Отчет о НИР. Структура и правила оформления

ГОСТ 7.80-2000 Библиографическая запись. Заголовок. Общие требования и правила составления

ГОСТ 19.701-90 (ИСО 5807-85) ЕСПД. Схемы алгоритмов, программ, данных и систем. Обозначения условные и правила выполнения

ГОСТ 34.601-90 Информационная технология. Комплекс стандартов на автоматизированные системы. Автоматизированные системы. Стадии создания

ГОСТ Р 50739-95 Средства вычислительной техники. Защита от несанкционированного доступа к информации. Общие технические требования

ГОСТ Р 1.5-2004 Стандарты национальные Российской Федерации. Правила построения, изложения, оформления и обозначения

ГОСТ Р 7.05-2008 СИБИД. Библиографическая ссылка. Общие требования и правила составления

2 Анализ предметной области

Известно, что максимальное количество информации на символ сообщения можно получить только в случае равновероятных и независимых символов. Реальные коды редко полностью удовлетворяют этому условию, поэтому информационная нагрузка на каждый их элемент обычно меньше той, которую они могли бы переносить. Раз элементы кодов, представляющих сообщения, недогружены, то само сообщение обладает информационной избыточностью.

Различают избыточность естественную и искусственную. Естественная избыточность характерна для первичных алфавитов, а искусственная – для вторичных.

Естественная избыточность может быть подразделена на семантическую и статистическую избыточности.

Семантическая избыточность заключается в том, что мысль, высказанная в сообщении, может быть выражена короче. Все преобразования по устранению семантической избыточности производятся в первичном алфавите.

Статистическая избыточность обусловливается не равновероятностным распределением качественных признаков первичного алфавита и их взаимозависимостью. Например, для английского языка избыточность составляет 50 %.

Устраняется статистическая избыточность путем построения эффективных неравномерных кодов. При этом статистическая избыточность первичного алфавита устраняется за счет рационального построения сообщений во вторичном алфавите.

При передаче сообщений, закодированных двоичным равномерным кодом, обычно не учитывают статистическую структуру передаваемых сообщений . Все сообщения (независимо от вероятности их появления) представляют собой кодовые комбинации одинаковой длины, т.е. количество двоичных символов, приходящихся на одно сообщение, строго постоянно.

Из теоремы Шеннона о кодировании сообщений в каналах без шумов следует, что если передача дискретных сообщений ведется при отсутствии помех, то всегда можно найти такой метод кодирования, при котором среднее число двоичных символов на одно сообщение будет сколь угодно близким к энтропии источника этих сообщений. На основании этой теоремы можно ставить вопрос о построении такого неравномерного кода, в котором часто встречающимся сообщениям присваиваются более короткие кодовые комбинации, а редко встречающимся символам – более длинные.

Таким образом, учет статистических закономерностей сообщения позволяет строить более экономный, более эффективный код.

Эффективным кодированием называется процедура преобразования символов первичного алфавита в кодовые слова во вторичном алфавите, при которой средняя длина сообщений во вторичном алфавите имеет минимально возможную для данного алфавита длину.

Эффективными называются коды, представляющие кодируемые понятия кодовыми словами минимальной средней длины. В литературе вместо термина “эффективное кодирование” часто используют так же термины оптимальное или статистическое кодирование.

Впервые идея эффективного кодирования была реализована Морзе. Например, в русском варианте Морзе буква “е” передается одной точкой, а редко встречающаяся буква “ц” – наоборот четырьмя символами.

Эффективность кодов определяется близостью энтропии источника сообщений и среднего числа двоичных знаков на букву кодов, т.е. в идеальном случае должно выполняться равенство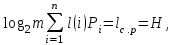



Для двоичных кодов и разность (L_cp - H) будет тем меньше, чем больше Н, а H достигает максимума при равновероятных и взаимно независимых символах. Отсюда вытекают основные свойства эффективных кодов:

• 
  минимальная средняя длина кодового слова оптимального кода обеспечивается в том случае, когда избыточность каждого кодового слова сведена к минимуму (в идеальном случае - к нулю);
  
• 
  кодовые слова оптимального кода должны строиться из равновероятных и взаимно независимых символов.
  

Из свойств оптимальных кодов вытекают принципы их построения.

Первый принцип эффективного кодирования: выбор каждого кодового слова необходимо производить так, чтобы содержащееся в нем количество информации было максимальным. Второй принцип эффективного кодирования заключается в том, что буквам первичного алфавита, имеющим большую вероятность, присваиваются более короткие кодовые слова во вторичном алфавите.

Принципы эффективного кодирования определяют методику построения эффективных кодов. [1, с. 59 – 60]

В учебном пособии по теории информации сигналов Ключко В.И., Власенко А.В., Кушнир Н.В., Кушнир А.В. говорится о преимуществе кода Хаффмана так «Преимущество метода Хаффмана сказывается при построении ОНК для вторичных алфавитов с m>2 . Большая точность достигается за счет более строгого выбора числа наименее вероятных символов первичного алфавита, объединяемых на первом этапе построения кодового дерева.» [1, с. 62].

Программа, реализующая алгоритм Хаффмана, была протестирована на

трех различных вариантах входных данных: на фразе «Jonny is real, really bad boy!», стихотворении Уильяма Блэйка «The tyger» и произведении Льюиса Кэрролла «Alice’s adventures in Wonderland». Язык входных данных был выбран английский для того, чтобы не подключать локализацию и во избежание различных ошибок. В таблицах 1 и 2 представлены результаты работы с первыми двумя вариантами, соответственно. Минимальная длина кода во всех случаях оказалась 3, а максимальные - 5, 10 и 16 символов, соответственно (рис. 1).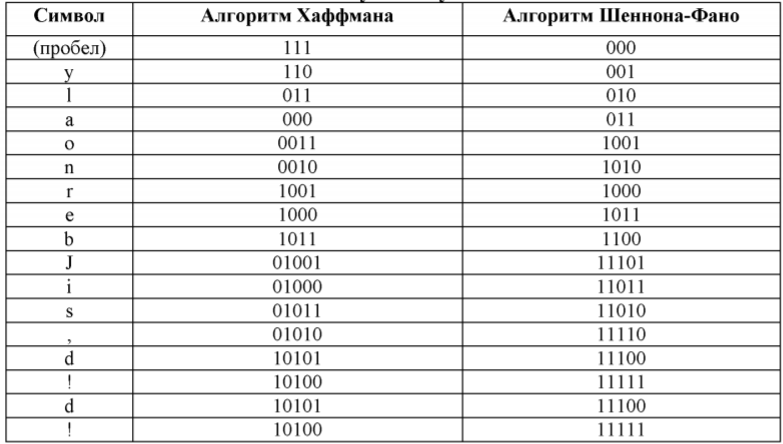



Рисунок 1 – Результаты работы алгоритма для фразы «Jonny is really, really bad boy!».

Следует отметить, что этот алгоритм был придуман давно, и в настоящее время существуют другие эффективные способы кодирования и сжатия данных.

3 Реализация

3.1 Среда разработки и организация решения

Данная курсовая работа выполнена в среде программирования MicrosoftVisualStudio 2019. Она является ведущей IDE для языка программирования С# и самая популярная среди программистов. Важно отметить, что в нашей работе используется решение формата WindowsForm, который доступен только в этой IDE. За пару минут мы можем создавать программы с самым простым интерфейсом без особых проблем, поскольку в неё заранее уже заложены шаблоны.

3.3 Реализация алгоритма Хаффмана

На сегодняшний день трудно переоценить значение информационных средств сообщения. Основная их цель – точно или приближенно воспроизвести в определенной точке пространства и времени некоторое сообщение, посланное из другой точки. В связи с этим возникает множество задач, в том числе, рассматриваемая нами, задача кодирования передаваемой информации. Для её решения мы используем популярный алгоритм Хаффмана, который служит основой для многих других программ и алгоритмов сжатия графической и текстовой информации. Алгоритм Хаффмана является алгоритмом оптимального префиксного кодирования информации с минимальной избыточностью. Алгоритм получает на входе массив значений частот встречаемости символов в кодируемом сообщении. Далее на основании этой таблицы строится дерево кодирования Хаффмана. Входные символы образованного алфавита создают список свободных узлов дерева, каждый из которых имеет вес, равный частоте встречаемости. Выбрав два свободных узла дерева с наименьшими весами, создается их родитель с весом, равным их суммарному весу. Родитель добавляется в список свободных узлов, а его потомки соединяются с ним дугами со значениями 0 и 1, при этом удаляются из списка свободных узлов. Шаги, начиная с выбора свободных узлов, повторяются до тех пор, пока в списке свободных узлов не останется только один свободный узел, который будет считаться корнем дерева

Чтобы определить код для каждого из символов, входящих в сообщение необходимо пройти путь от узла дерева соответствующего текущему символу, до его корня, накапливая биты при перемещении по ветвям дерева. Полученная таким образом последовательность битов является кодом данного символа, записанным в обратном порядке. Основными объектами в нашей реализации являются два класса – Node и HuffmanTree, обозначающие узел и дерево Хаффмана соответственно. Класс Node содержит переменные Symbol – символ, Frequency – частота, Right – правый дочерний узел, Left – левый дочерний узел (рис. 2).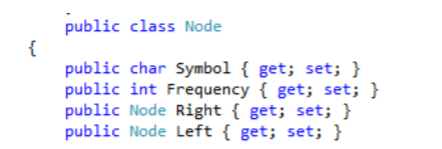



Рисунок 2 - Переменные класса Node

Класс HuffmanTree состоит из переменных nodes – список узлов типа Node, Root – корень дерева, Frequencies – алфавит с количеством повторений каждого символа (рис. 3)

Рисунок 3 - Переменные класса HuffmanTree

По поступающей строке source метод Build класса HuffmanTree формирует алфавит в переменной Frequencies с подсчетом частот. Далее для каждого символа в алфавите создаем узлы дерева, добавляемые в список nodes. Теперь мы имеем первоначальный список свободных узлов (рис. 4).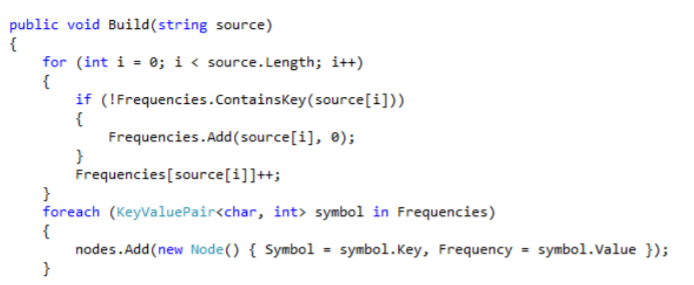

Рисунок 4 - Метод Build (часть № 1)

Пока в списке не останется единственный узел – корень дерева, производим циклично следующие действия: упорядочиваем свободные узлы по возрастанию в список orderedNodes; берем первые два узла этого списка; создаем из них родительский узел согласно алгоритму, левый и правый дочерние узлы сохраняем в соответствующих переменных узла; удаляем дочерние узлы из списка свободных, добавляем туда родительский узел (рис. 5).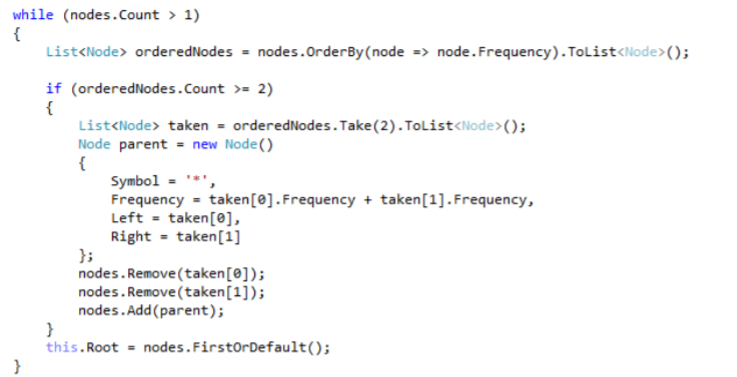

Рисунок 5 -Метод Build (часть № 2)

Таким образом, вся структура дерева хранится в дочерних узлах корня дерева. Каждый дочерний узел, кроме первоначальных свободных узлов, имеют свои дочерние узлы. Теперь, когда дерево построено, нужно произвести кодирование каждого символа сообщения. Метод Encode класса HuffmanTree для каждого символа вызывает метод Traverse класса Node, производящий обход дерева и возвращающий двоичный код символа. Все коды последовательно добавляются в список булевых значений encodedSourse, который в конце преобразуется в единый массив битов bits и является конечным результатом кодирования (рис. 6).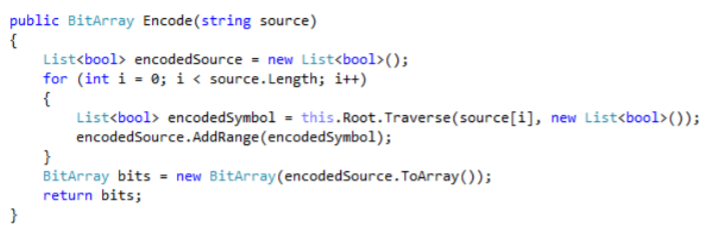

Рисунок 6 - Метод Encode

Наибольший интерес представляет метод Traverse. Метод является рекурсивным, поэтому вначале он проверяет, если узел не имеет дочерних узлов, соответствует ли текущий символ в узле входному изначально для кодирования символу. Если же узел является родительским, то идем сначала по левому узлу, в переменную leftPath добавляем ранее накопленные биты и бит равный нулю, вызываем метод Traverse по этому левому узлу, сохранив его результат в переменную left. Далее идем по правому узлу, выполняя аналогичные действия, как и для левого узла. В конечном счете, переменная left или right будет содержать необходимый набор битов для кодирования символа (рис. 7).

Переданное закодированное сообщение нужно декодировать. Так как информация об алфавите и частотах его символов передается вместе с сообщением, то структура дерева Хаффмана восстанавливается. Благодаря тому, что не имеется ни одного кодового значения символа, которое было бы началом любого другого кодового значения символа, можно последовательно однозначно декодировать сообщение. Метод Decode класса HuffmanTree побитно производит движение по дереву от корня, и, достигая конечного узла, добавляет значение символа в переменную decoded, что повторяется до конца закодированного сообщения (рис. 8).



Рисунок 7 - Метод Traverse



Рисунок 8 - Метод Decode

3.2 Описание программы

Добавляем в форму четыре элемента richTextBox, один элемент treeView и кнопку button1. Первый элемент richTextBox1 предназначен для ввода текста, который будет кодироваться. В treeView1 показывается таблица с алфавитом кодов Хаффмана. В элементе richTextBox2 выводится массив бит. В richTextBox4 идёт перевод в массив бит Хаффмана. И в элементе richTextBox3 происходит обратный перевод в текст.



Рисунок 9 – Архиватор

Заключение

В процессе выполнения курсовой работы разработана программа, демонстрирующаяработу эффективность кода Хаффмана.

Во время выполнения задания на данную курсовую работу были получены углублённые знания по дисциплине «Теория информации и сигналов», в частности, были подробно изучены статистические характеристики стационарных случайных сигналов и приобретены практические навыки для работы со средой разработки MicrosoftVisualStudio 2019.

В ходе выполнения данной курсовой работы были получены углублённые навыки по разработке программного обеспечения на языке программирования C# в среде разработки VisualStudio C# 2019.

В перспективе данная программа может быть использована в качестве одного из компонентов более сложных программ, имеющих похожую направленность.

Прилагаю приложение разработанной и тестированной программы «Реализация кода Хаффмана в архиваторе» с оригинальностью 69,65%.

Список используемой литературы

Основная

1. Ключко В.И., Власенко А.В., Кушнир Н.В., Кушнир А.В. Теория информации и сигналов: учеб. пособие / Кубан. гос. технол. ун-т.- Краснодар: Изд. ФГБОУ ВПО «КубГТУ», 2014. 59, 61 с.

2. Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ . 2-е изд. М.: Вильямс, 2006. 1296 с.

3. Сэломон Д. Сжатие данных, изображения и звука. М.: Техносфера, 2004. 368 с.

4. Левитин А. В. Глава 9. Жадные методы: Алгоритм Хаффмана // Алгоритмы. Введение в разработку и анализ. М.: Вильямс, 2006. С. 392-398. 576 с.

5. Марков А. А. Введение в теорию кодирования. М.: Наука, 1982. 192с

.Интернет ресурсы

6. Код Хаффмана [электронный ресурс]. Адрес доступа https://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D0%B4_%D0%A5%D0%B0%D1%84%D1%84%D0%BC%D0%B0%D0%BD%D0%B0

Приложение А – Скриншот проверки курсовой работы в системе Antiplagiat.ru3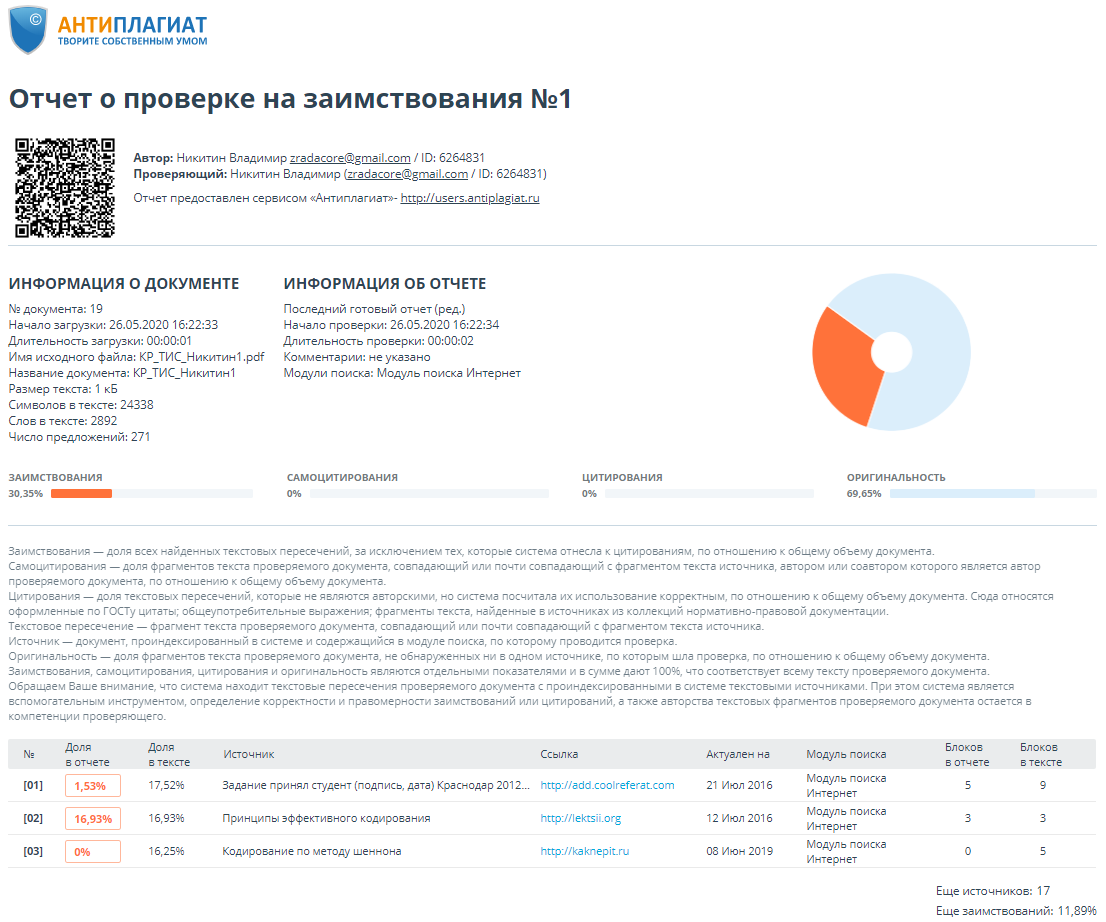

Приложение Б – Листинг программы «Реализация кода Хаффмана в архиваторе»

using System;

using System.Collections;

using System.Collections.Generic;

using System.ComponentModel;

using System.Data;

using System.Drawing;

using System.Linq;

using System.Text;

using System.Threading.Tasks;

using System.Windows.Forms;
namespace Hamming

{

public partial class Form1 : Form

{

public Form1()

{

InitializeComponent();

}
///

/// Структура "узел H-дерева"

///

public struct huffmannTreeNode

{

///

/// Текст

///

public String text;

///

/// Двоичный код

///

public String code;

///

/// Частота встречаемости

///

public int frequency;
public huffmannTreeNode(String t, String c, int f)

{

text = t;

code = c;

frequency = f;

}

};
///

/// Частота встречаемости отдельных символов алфавита

///

Dictionary freqs = new Dictionary();

///

/// Исходное дерево

///

List source = new List();

///

/// Вспомогательное дерево

///

List newRes = new List();

///

/// Еще дерево

///

List tree = new List();

///

/// Сортировка узлов дерева по убыванию

///

void sortTree()

{

for (int index = 0; index < tree.Count - 1; index++)

{

for (int index2 = index; index2 < tree.Count; index2++)

{

if (tree[index].frequency < tree[index2].frequency)

{

huffmannTreeNode buf = tree[index];

tree[index] = tree[index2];

tree[index2] = buf;

}

}

}

}
private void button1_Click(object sender, EventArgs e)

{

String text = richTextBox1.Text;
//Считаем частоту

for (int index = 0; index < richTextBox1.Text.Length; index++)

{

if (freqs.Keys.Contains(text[index]))

{

freqs[text[index]]++;

}

else

{

freqs.Add(text[index], 1);

}

}
//Начальное заполнение деревьев

foreach (KeyValuePair Pair in freqs)

{

source.Add(new huffmannTreeNode(Pair.Key.ToString(), "", Pair.Value));

tree.Add(new huffmannTreeNode(Pair.Key.ToString(), "", Pair.Value));

newRes.Add(new huffmannTreeNode(Pair.Key.ToString(), "", Pair.Value));

}
//Переводим в байты

String textAsBytes = "";

BitArray btr = new BitArray(Encoding.ASCII.GetBytes(text));
for (int index = 0; index < btr.Count; index++)

{

textAsBytes += (btr[index] ? "1" : "0");

}
label1.Text = btr.Count.ToString() + "(" + freqs.Count.ToString() + ")";

richTextBox2.Text = textAsBytes;

//Строим дерево

while (tree.Count > 1)

{

sortTree();
for (int index = 0; index < source.Count; index++)

{

if (tree[tree.Count - 2].text.Contains(source[index].text))

{

newRes[index] = new huffmannTreeNode(newRes[index].text, "0" + newRes[index].code, newRes[index].frequency);

}

else if (tree[tree.Count - 1].text.Contains(source[index].text))

{

newRes[index] = new huffmannTreeNode(newRes[index].text, "1" + newRes[index].code, newRes[index].frequency);

}

}
tree[tree.Count - 2] = new huffmannTreeNode(tree[tree.Count - 2].text + tree[tree.Count - 1].text, "",

tree[tree.Count - 2].frequency + tree[tree.Count - 1].frequency);

tree.RemoveAt(tree.Count - 1);

}
//Выводим алфавит на экран

treeView1.Nodes.Clear();

for (int index = 0; index < source.Count; index++)

{

treeView1.Nodes.Add(newRes[index].text + " (" + newRes[index].code + ")");

}
//Битовая последовательность с новыми кодами

for (int index = 0; index < text.Length; index++)

{

foreach (huffmannTreeNode htn in newRes)

{

if (htn.text == text[index].ToString())

{

richTextBox4.Text += htn.code;

}

}

}
label2.Text = richTextBox4.Text.Length.ToString();

//Кодируем обратно в буквы

String encodedText = richTextBox4.Text;

for (int index = 0; index < encodedText.Length - 7; index += 8)

{

int code = 0;

for (int ind = 0; ind < 8; ind++)

{

if (encodedText[index + ind] == '1')

{

code += Convert.ToInt32(Math.Pow(2, 7 - ind));

}

}

richTextBox3.Text += (char)code;

}
//Дописываем алфавит в новую строку (чтобы раскодировать было можно)

}
private void button2_Click(object sender, EventArgs e)

{
}
private void richTextBox2_TextChanged(object sender, EventArgs e)

{
}
private void richTextBox4_TextChanged(object sender, EventArgs e)

{
}
private void richTextBox1_TextChanged(object sender, EventArgs e)

{
}

}

}

Приложение В – Результаты работы программы «Реализация кода Хаффмана в архиваторе»