МЭТ2. МЭТ_Готовая_2. Исследование электрических свойств полупроводниковых материалов
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина) Кафедра Микро- и наноэлектроники отчет по лабораторной работе №2 Тема: «Исследование электрических свойств полупроводниковых материалов».
Санкт-Петербург 2022 Цель работы Сравнение температурных зависимостей сопротивления полупроводников с различной шириной запрещенной зоны; определение ширины запрещенной зоны и энергии ионизации легирующих примесей в материалах. Теоретические положения Полупроводники – материалы с электронной электропроводностью, которые по своему удельному сопротивлению занимают промежуточное положение между проводниками и диэлектриками. Условный диапазон удельных сопротивлений полупроводников ограничивают значениями 10–5... 108 Ом∙м. Характерной особенностью полупроводниковых материалов является сильно выраженная зависимость удельной проводимости от внешних энергетических воздействий, а также от концентрации и типа примесей. В зависимости от степени чистоты полупроводники подразделяются на собственные и примесные. Собственный – это такой полупроводник, в котором можно пренебречь влиянием примесей при данной температуре. Содержание примесей в них не превышает 10-9…10-8 %, и существенного влияния на удельную проводимость полупроводника они не оказывают. Примесный – это такой полупроводник, электрофизические свойства которого в основном определяются примесями. В собственных полупроводниках все валентные электроны атомов участвуют в образовании ковалентной (или ионно-ковалентной) насыщенной химической связи. При T = 0 К в полупроводниковых кристаллах нет ни одного квазисвободного носителя заряда, способного принять участие в направленном движении при воздействии внешнего фактора, т. е. при температуре абсолютного нуля полупроводник не обладает электропроводностью. Прочность ковалентной (ионно-ковалентной) связи (энергия связи) соответствует ширине запрещенной зоны полупроводника ∆Э. При температурах, отличных от 0 К, часть носителей заряда за счет тепловых флуктуаций способна разорвать химическую связь, что приводит к образованию равного количества электронов ni в зоне проводимости и дырок pi в валентной зоне. Экспериментальные данные и обработка результатов эксперимента 1. Рассчитать удельное сопротивление исследуемых полупроводниковых материалов по экспериментальным данным для каждой температурной точки по формуле ρ = RS/l. Вычислить соответствующие удельные проводимости образцов γэксп = 1/ρ. Результаты занести в таблицу 1.
2. По данным таблицы 1 построить температурные зависимости удельной проводимости полупроводников, откладывая по оси абсцисс параметр T−1, а по оси ординат – экспериментальные значения lnγэксп. 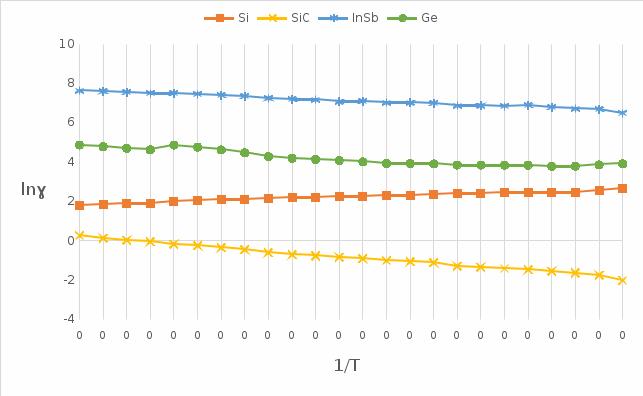 Рис 1. Температурные зависимости удельной проводимости полупроводников. 3. Рассчитать концентрации собственных носителей заряда в полупроводниках Si, Ge, InSb и SiC при T = 300 К по формуле ni = pi = (Nc∙Nv)1/2∙exp(-∆Э/(2kT)). ni (Si) = 6.76∙1015 м-3 ni (Ge) = 2,28∙1019 м-3 ni (SiC) = 7.66 м-3 ni (InSb) = 4.71∙1022 м-3 4. Оценить значения собственной удельной проводимости в этих полупроводниках при 300 К: γi = q∙n(µn + µp). γi (Si) = 5,74∙1,6∙10-4 (0,13 + 0,05) = 1,9∙10-4 См/м γi (Ge) = 2,07∙1,6(0,39 + 0,19) = 2.11 См/м γi (SiC) = 5,01∙1,6∙10-19(0,04 + 0,006) = 0,56∙10-19 См/м γi (InSb) = 1,45∙1,6∙103(7,8 + 0,075) = 18,773∙103 См/м 5. Сравнивая полученные в результате расчетов значения γi со своими экспериментальными данными γэксп, решить, какие же носители (собственные или примесные) определяют электрическую проводимость исследуемых образцов в интервале температур от Tmin = 300 К до Тmax – максимальной температуры измерений. Si: γэксп >> γi. Наблюдается только примесная электропроводность. Энергия ионизации примеси ∆Эпр = 0,01 … 0,02 < kTmax = 0,035. Ge: γэксп ≈ γi. Наблюдается собственная электропроводность. SiC: γэксп >> γi, следовательно, наблюдается только примесная электропроводность. Энергия ионизации примеси ∆Эпр = 0,04 … 0,4 > kTmax = 0,035 – не все примеси ионизированы. InSb: γэксп ≈ γi, следовательно, наблюдается собственная электропроводность. 6. Если в полупроводнике не все примеси ионизированы, то по наклону кривой lnγэксп(1/Т) можно найти ∆Эпр: ∆Эпр = 2k[T2T1(T2-T1)-1∙ln{n(T2)/n(T1)}] nэксп = γэксп/[q(µn + µp)] ∆Эпр (SiC) = 0,74 эВ 7. Для полупроводников, у которых γэксп ≈ γi, определить ∆Э по формуле: ∆Э = 2kT2T1(T2-T1)-1[ln{n(T2)/n(T1)}-1,5ln(T2/T1)] ∆Э (Ge) = 0,77 эВ ∆Э (InSb) = 0,061 эВ. Вывод В ходе выполнения лабораторной работы были получены температурные зависимости проводимости полупроводников. Проводимость примесного полупроводника определяется концентрацией носителей и их подвижностью. С изменением температуры подвижность носителей меняется по сравнительно слабому закону, а концентрация носителей – по очень сильному, поэтому проводимость примесных полупроводников определяется в основном температурной зависимостью концентрации носителей в нем. По полученным данным и графикам можно сделать выводы: Для InSb γэксп ≈ γi, что свидетельствует о наличии собственной проводимости. Полученный участок графика описывает собственную электропроводность. У Ge также наблюдается собственная проводимость. Полученная зависимость иллюстрирует переход от примесной к собственной проводимости. Ge и InSb являются узкозонными полупроводниками, у которых собственная концентрация носителей заряда при комнатной и близкой к ней температуре велика. Для SiC γэксп >> γi, следовательно, наблюдается только примесная проводимость. Полученный участок является участком ионизации примесей. Для Si γэксп >> γi. Наблюдается только примесная электропроводность. По графику можно говорить о наличии зоны истощения. 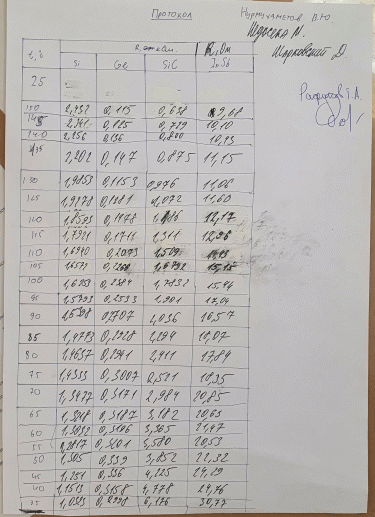 |
