ЛР №1. Исследование электрических свойств проводниковых материалов
 Скачать 294.5 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра физики отчет по лабораторной работе №1 по дисциплине «МЭТ» Тема: Исследование электрических свойств проводниковых материалов.
Санкт-Петербург 2022 Основные понятия и определения. Проводниковыми называют материалы, основным электрическим свойством которых является сильно выраженная электропроводность. К основным электрическим характеристикам проводниковых материалов относят: удельное сопротивление ρ, температурный коэффициент удельного сопротивления αρ, удельную термоэлектродвижущую силу αТ. В процессе направленного движения электроны испытывают рассеяние на статических (атом, вакансии, междоузельные атомы и т.д.) и динамических (тепловые колебания ионов в узлах кристаллической решётки) дефектах структуры. Интенсивность рассеяния определяет среднюю длину свободного пробега электрона и значение удельного сопротивления проводника, которое может быть выражено следующим образом:  , где m – масса электрона, e – заряд электрона,  - средняя скорость теплового движения, n0 – концентрация свободных электронов,  - средняя длина свободного пробега.Концентрация электронов и средняя скорость их теплового движения в металлах слабо зависит от температуры (электронный газ – вырожденный), но с повышением температуры увеличивается амплитуда колебаний ионов в узлах кристаллической решётки, что приводит к более интенсивному рассеянию электронов в процессе их направленного движения. Соответственно уменьшается средняя длина свободного пробега и возрастает удельное сопротивление. Относительное изменение удельного сопротивления при изменении температуры на один Кельвин называют температурным коэффициентом удельного сопротивления:  В области линейной зависимости  справедливо выражение: , где  и  - удельное сопротивление и температурный коэффициент удельного сопротивления, отнесённые к температуре  .Полное удельное сопротивление сплава:  , где  - сопротивление, обусловленное рассеянием электронов на тепловых колебаниях узлов решётки;  - добавочное (остаточное) сопротивление, связанное с рассеянием электронов на неоднородностях структуры сплава. Для многих двухкомпонентных сплавов изменение остаточного сопротивления от состава хорошо описывается параболической зависимостью вида: , где  ,  - атомные доли компонентов в сплаве.Удельное сопротивление тонких металлических плёнок существенно превосходит удельное сопротивление массивного металла. Для сравнительной оценки поводящих свойств плёнок пользуются таким параметром как сопротивление квадрата поверхности  , где  - удельное сопротивление слоя толщиной d.При соприкосновении двух различных металлов между ними возникает контактная разность потенциалов. Термоэлемент, составленный из двух различных проводников, образующих замкнутую цепь, называют термопарой. При различной температуре контактов в замкнутой цепи возникает термоэлектрический ток. Если цепь разорвать в произвольном месте, то на концах разомкнутой цепи появится термоэлектродвижущая сила. В относительно небольшом температурном интервале термоЭДС пропорциональна разности температур контактов (спаев):  .Описание установки. Измерение сопротивления исследуемых проводников и термоЭДС термопар производится с помощью ампервольтметра, постоянно подключённого к испытательному стенду. Все исследуемые образцы расположены в корпусе стенда, причём резисторы R1, R2, R3 и один из спаев термопар помещены в термостат. Обработка результатов. Таблица 1.1
Таблица 1.2
1. Расчёт удельного сопротивления металлических проводников и сопротивления квадрата поверхности металлических плёнок:  , где R – сопротивление образца, S – площадь поперечного сечения, l – длина проводника. , где R сопротивление образца, b – ширина резистивного слоя, l – длина плёнки.Таблица 1.2
2. Зависимость сопротивления материалов от температуры: 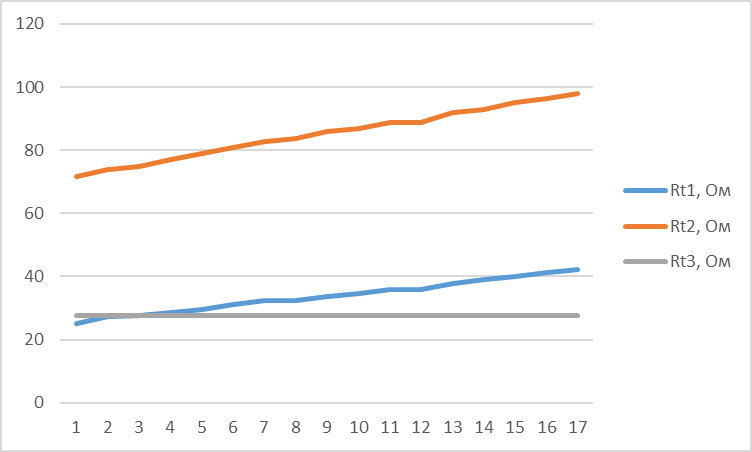 3. Расчёт температурного коэффициента удельного сопротивления:  , где  и  - температурные коэффициенты сопротивления и линейного расширения. , где  - сопротивление образца при данной температуре.Таблица 1.3
4. Зависимость температурного коэффициента удельного сопротивления от температуры: 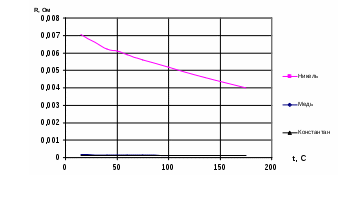 5. Зависимость удельного сопротивления и температурного коэффициента удельного сопротивления от состава для слава Cu-Ni:  , где a – постоянный коэффициент (a = 1,82), х – содержание никеля в сплаве в относительных долях по массе. Таблица 1.5
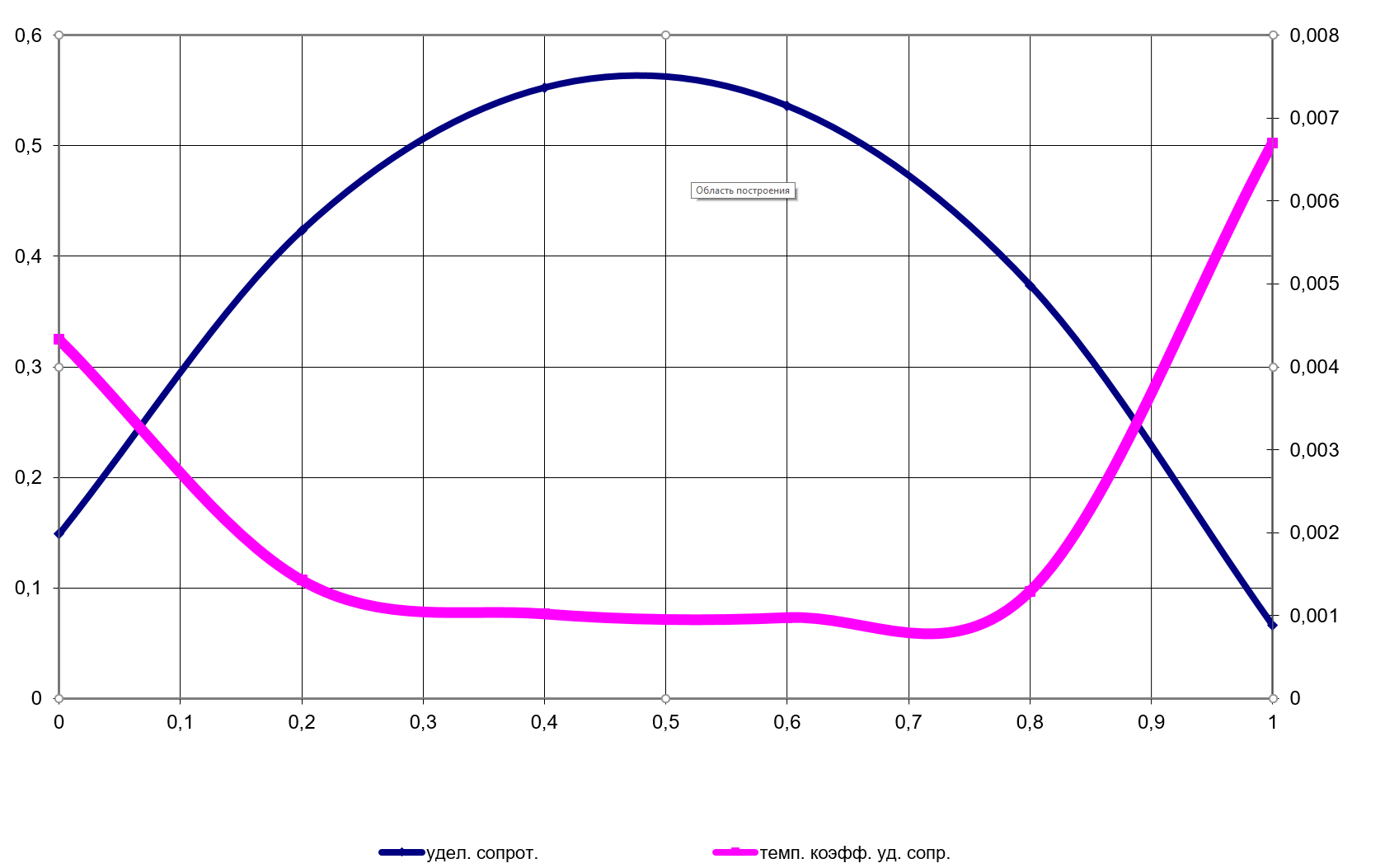 Таблица 1.4
6. Температурная зависимость термоЭДС: 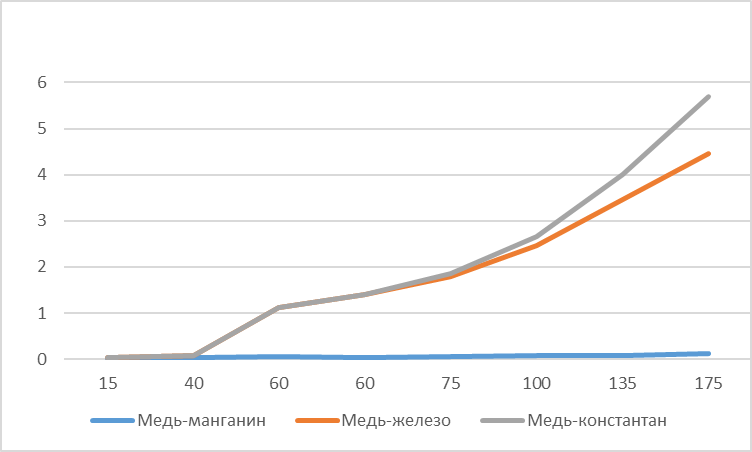 Вывод В результате выполнения лабораторной работы были исследованы электрические свойства проводниковых материалов. Для достижения результатов было выполнено: -измерение сопротивлений объемных и тонкопленочных резисторов на лабораторном стенде. -исследование зависимостей удельных электрических сопротивлений и их температурных коэффициентов от температуры и состава резистивных материалов, а также зависимостей термоЭДС термопар от разностей температур контактов Научился находить удельное сопротивление проволоки, а также удельное поверхностное сопротивление проводящей плёнки. У сплава меди и никеля - константана, удельное сопротивление, с повышением температуры изменяется незначительно относительно изменения удельного сопротивления меди и никеля при тех же температурах. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||