Исследование функции.
Экстремумы и интервалы монотонности функции.
Функция  называется возрастающей на интервале называется возрастающей на интервале 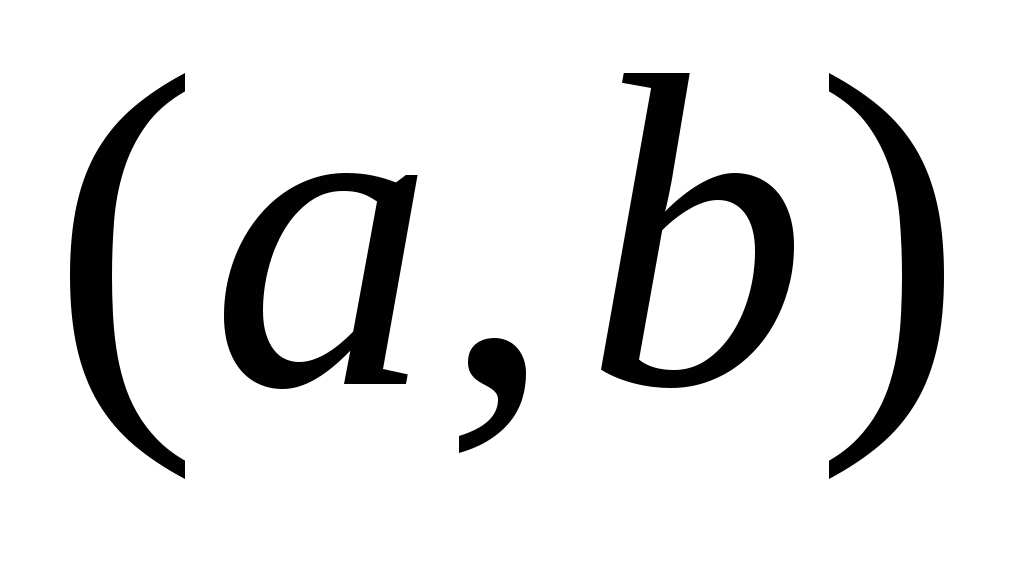 , если для любых точек , если для любых точек 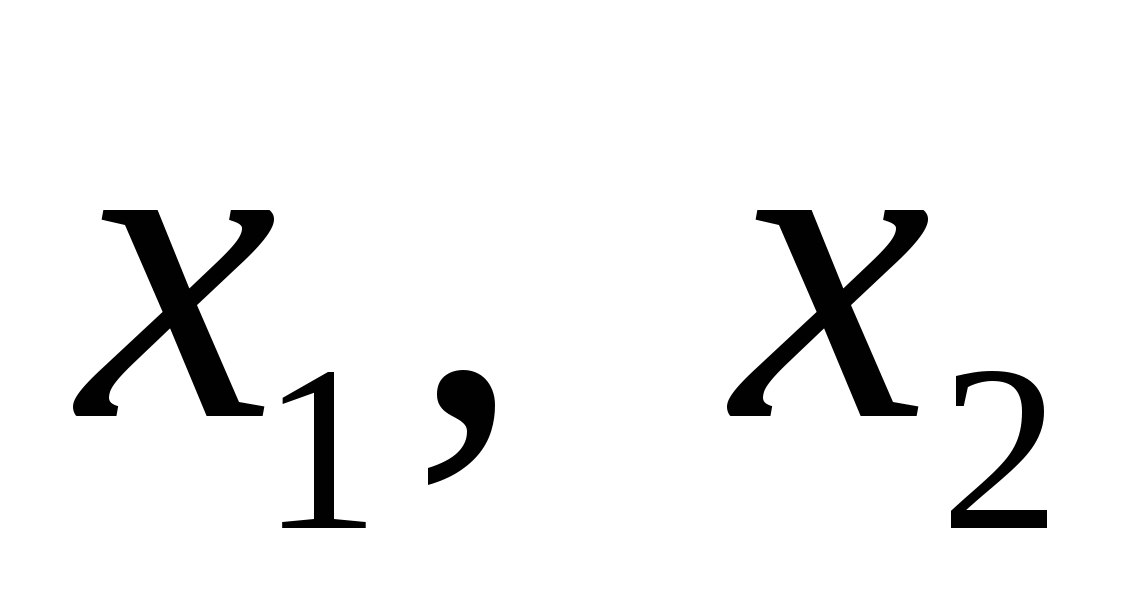 из этого интервала при выполнении условия из этого интервала при выполнении условия 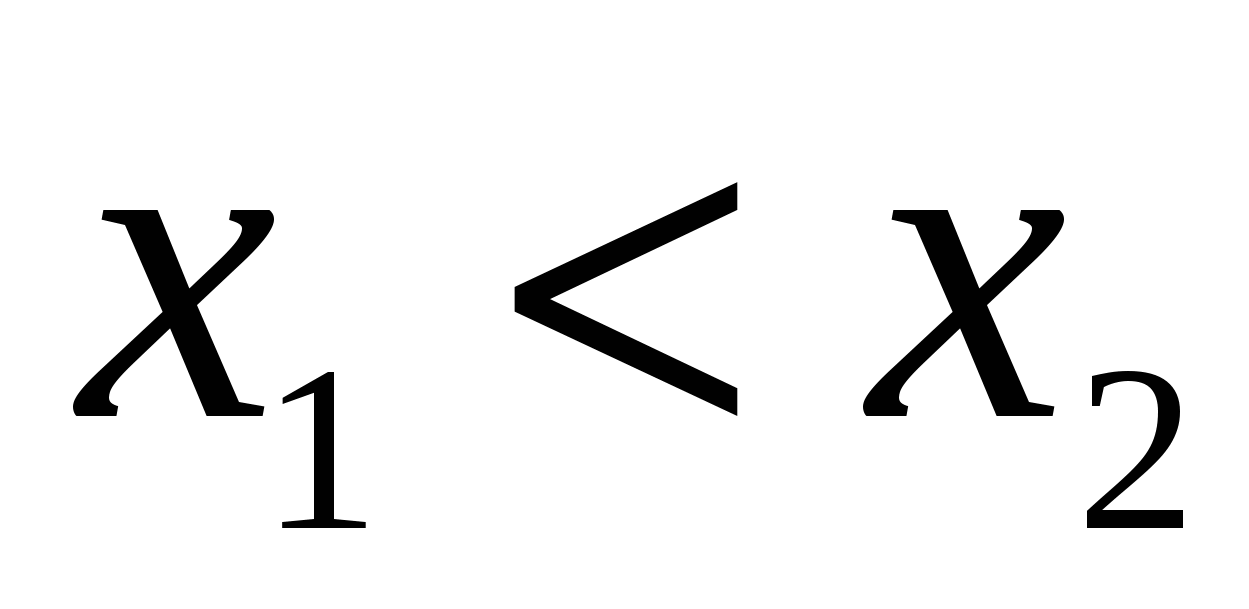 выполняется неравенство выполняется неравенство 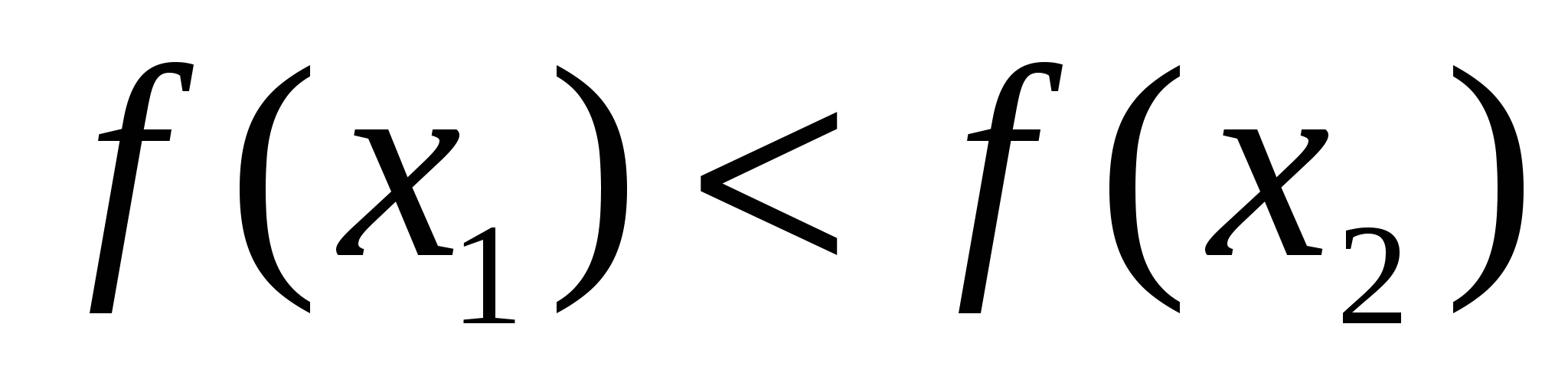 (большему значению аргумента соответствует большее значение функции). (большему значению аргумента соответствует большее значение функции).
Аналогично, функция  называется убывающей на интервале называется убывающей на интервале 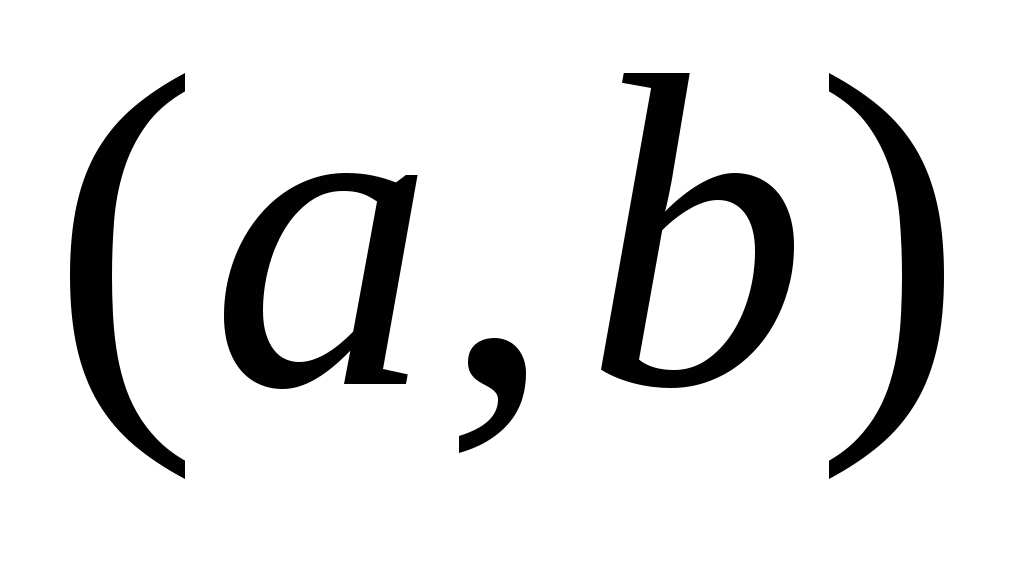 , если для любых точек , если для любых точек 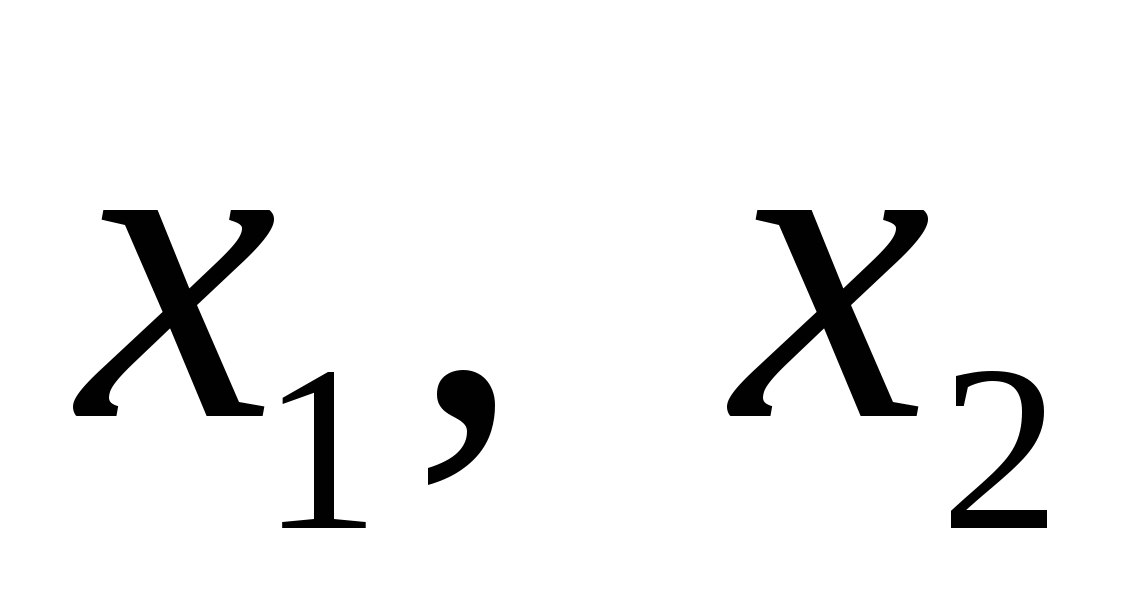 из этого интервала при выполнении условия из этого интервала при выполнении условия 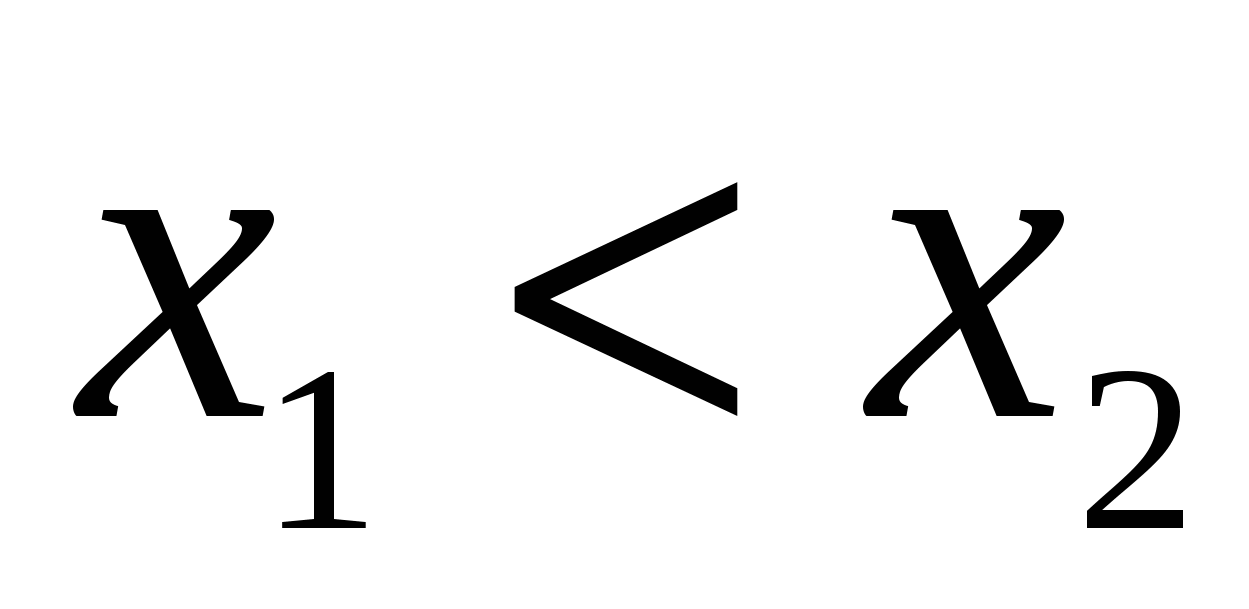 выполняется неравенство выполняется неравенство 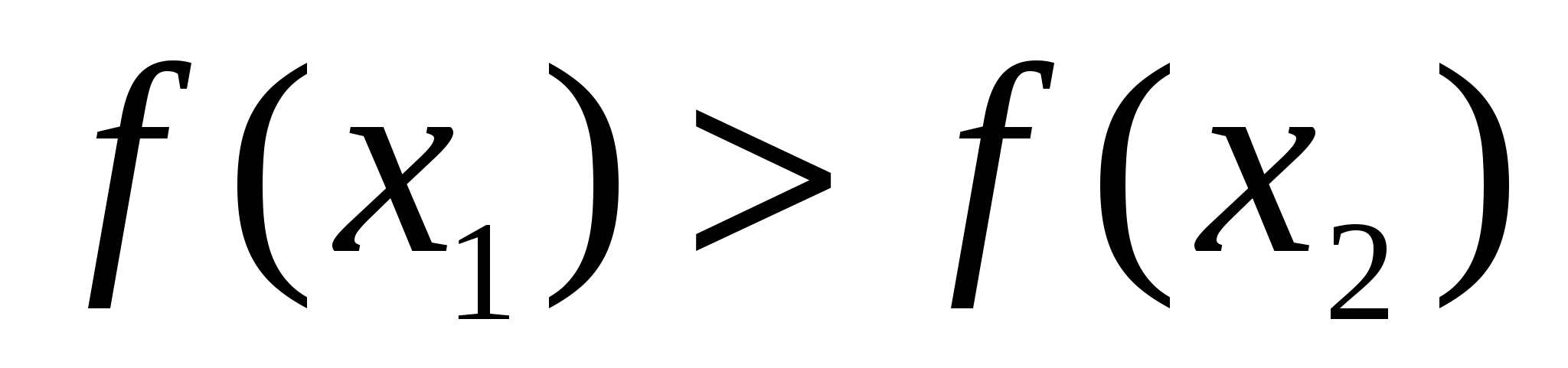 (большему значению аргумента соответствует меньшее значение функции). (большему значению аргумента соответствует меньшее значение функции).
Возрастающие на интервале 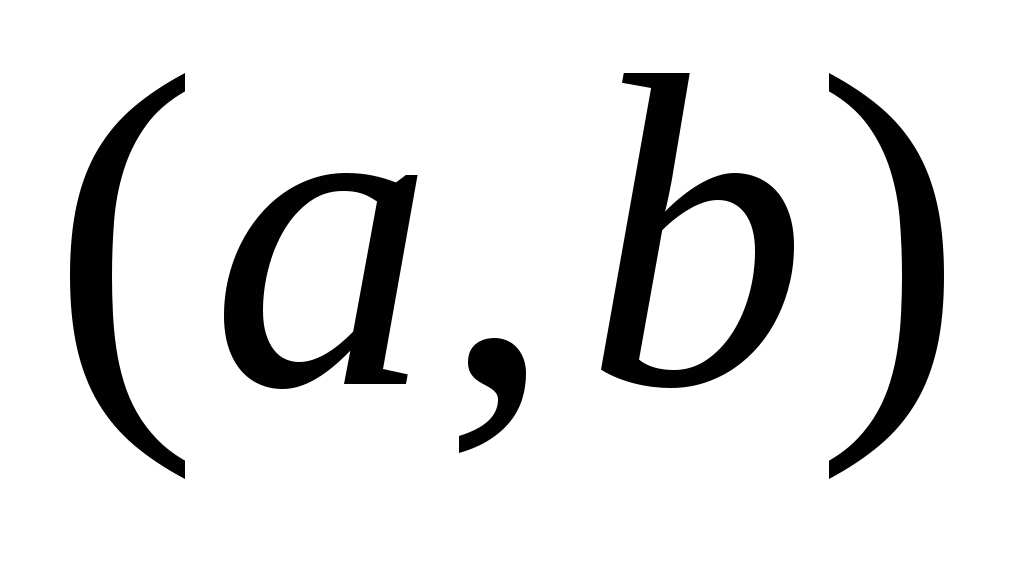 и убывающие на интервале и убывающие на интервале 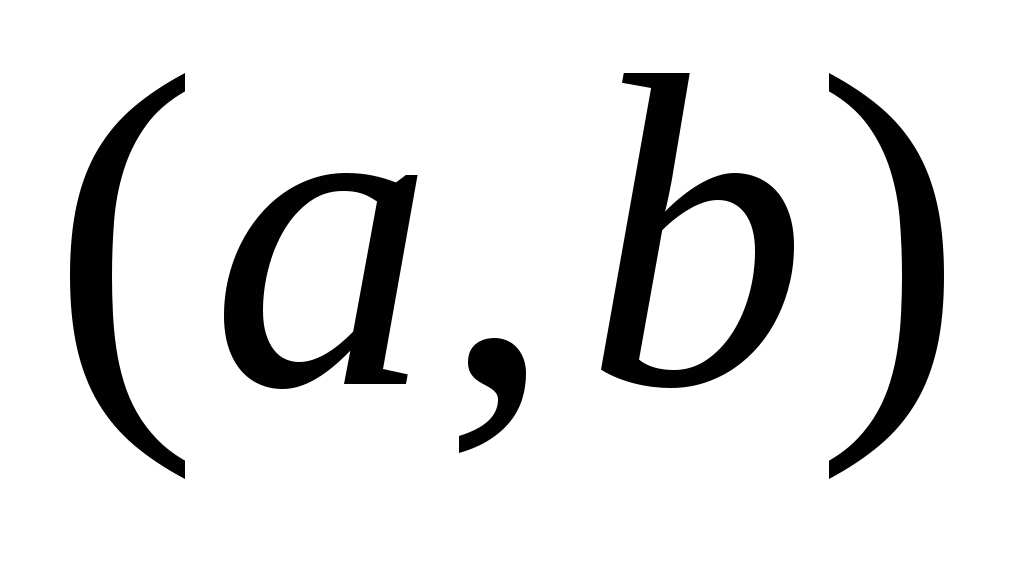 функции называются монотонными на интервале функции называются монотонными на интервале 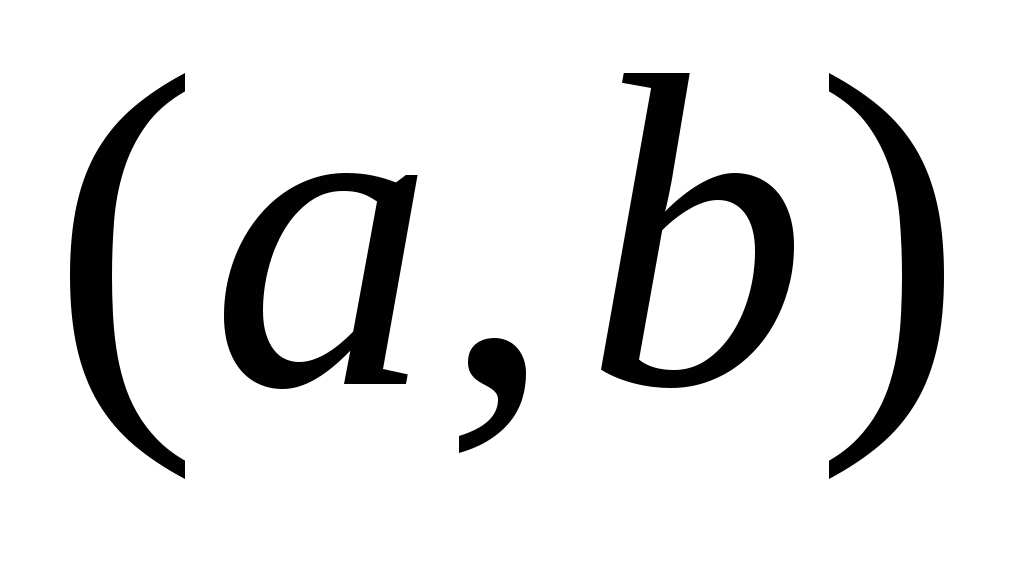 . .
Знание производной дифференцируемой функции позволяет находить интервалы ее монотонности.
Теорема (достаточное условие возрастания функции). Если производная дифференцируемой на интервале 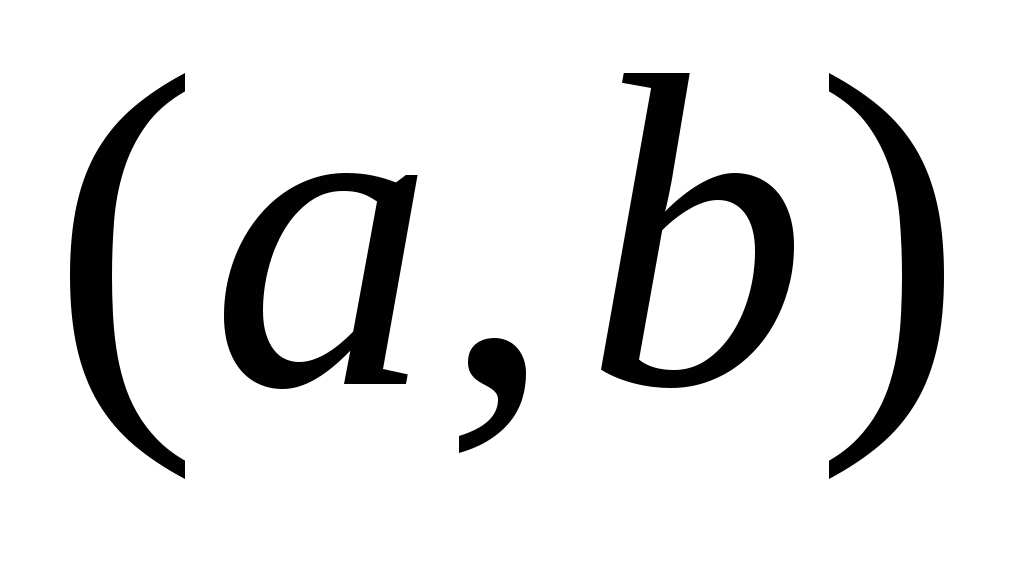 функции функции  положительна на интервале положительна на интервале 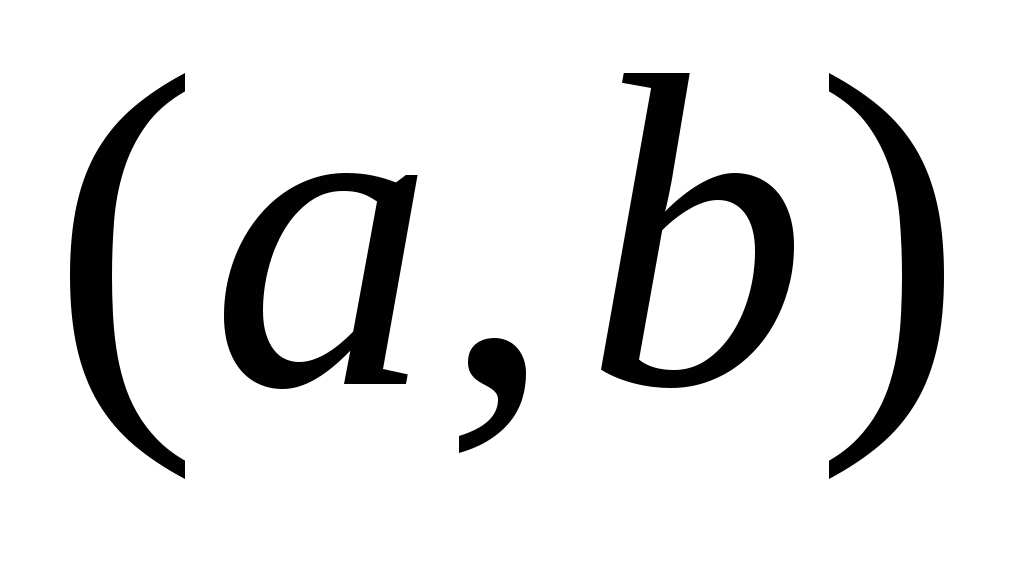 , то функция , то функция  монотонно возрастает на этом интервале. монотонно возрастает на этом интервале.
Теорема (достаточное условие убывания функции). Если производная дифференцируемой на интервале 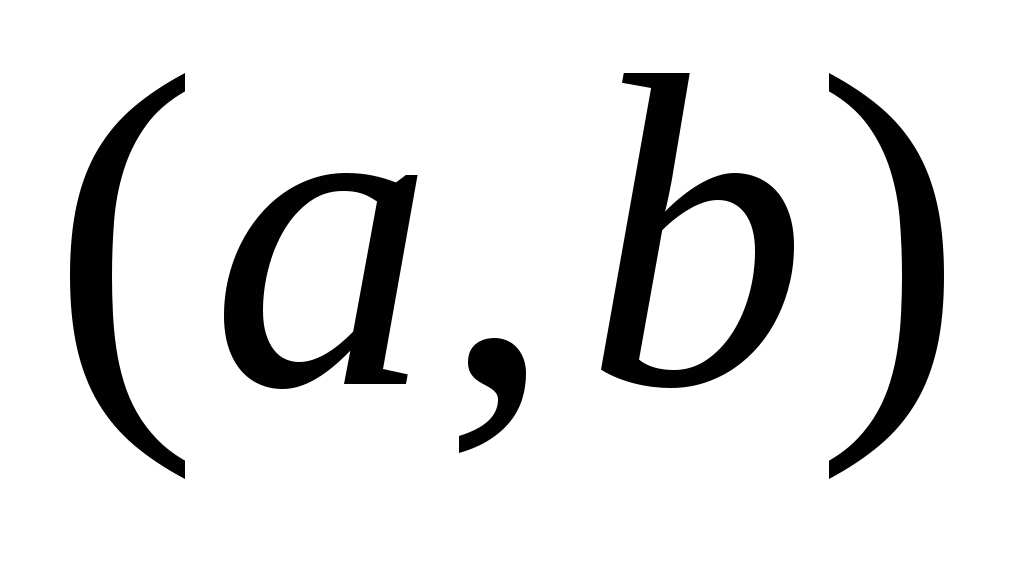 функции функции  отрицательна на интервале отрицательна на интервале 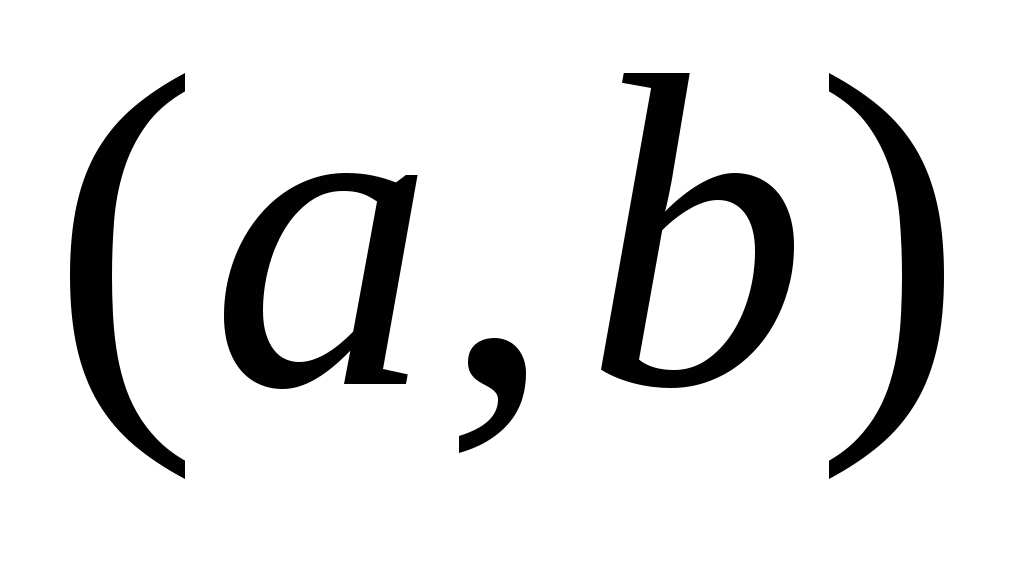 , то функция , то функция  монотонно убывает на этом интервале. монотонно убывает на этом интервале.
Геометрический смысл этих теорем состоит в том, что на интервалах убывания функции касательные к графику функции образуют с осью 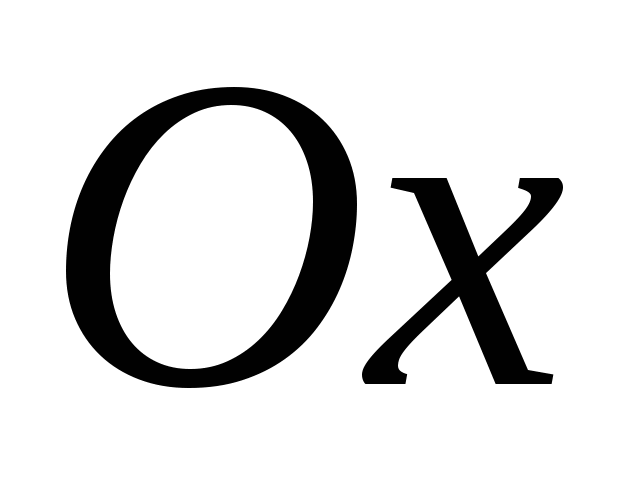 тупые углы, а на интервалах возрастания – острые (см. рис. 1). тупые углы, а на интервалах возрастания – острые (см. рис. 1).
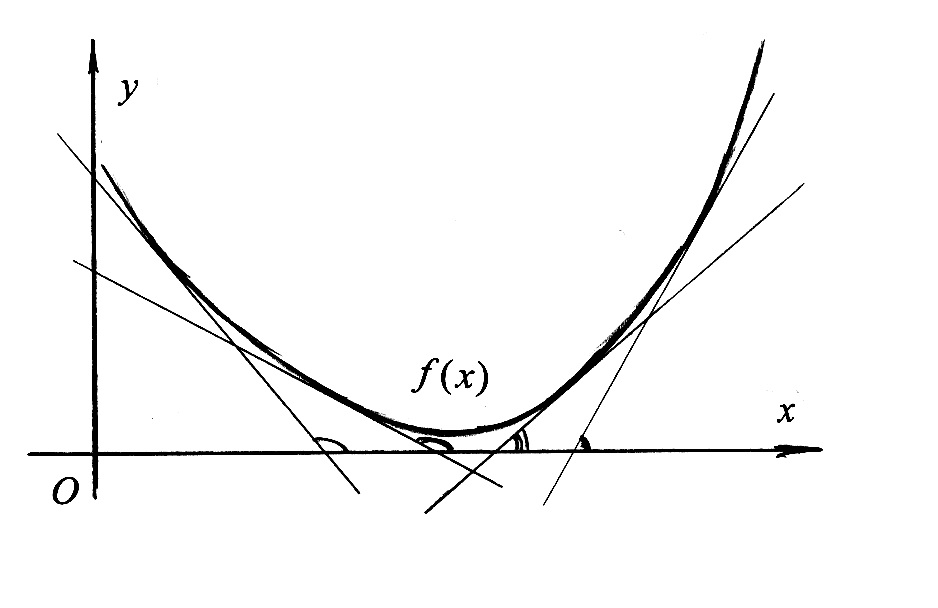
Рис. 1.
Теорема (необходимое условие монотонности функции). Если функция  дифференцируема и дифференцируема и 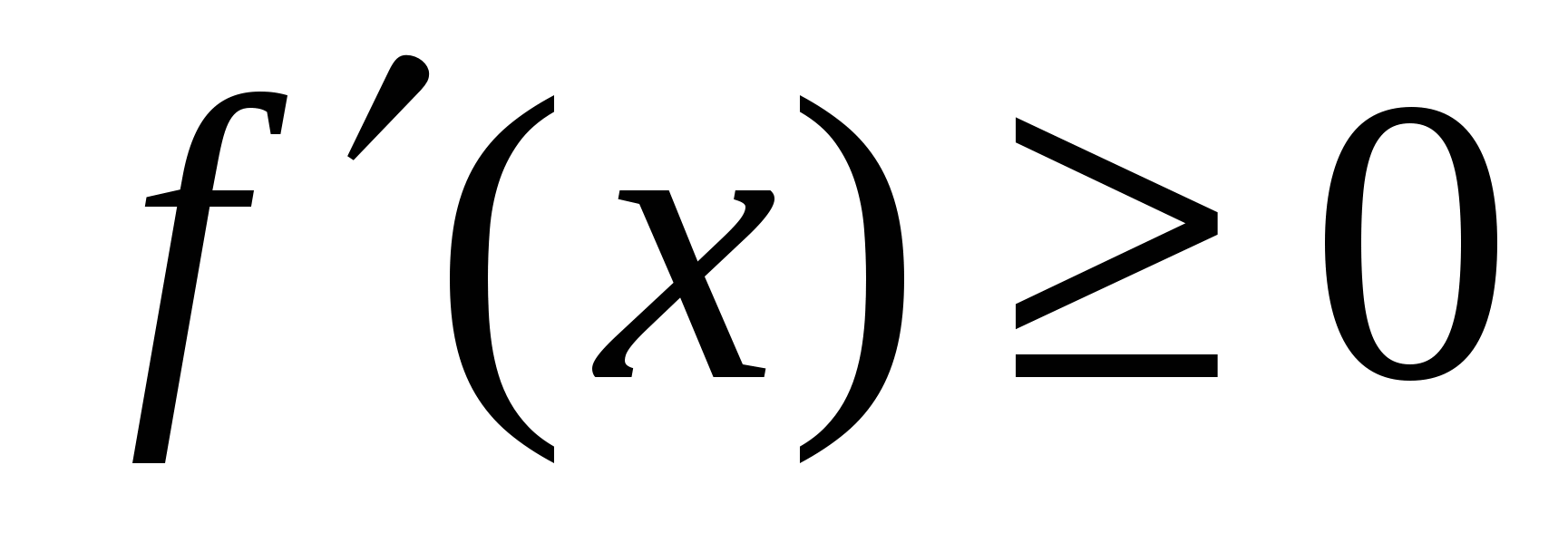 ( (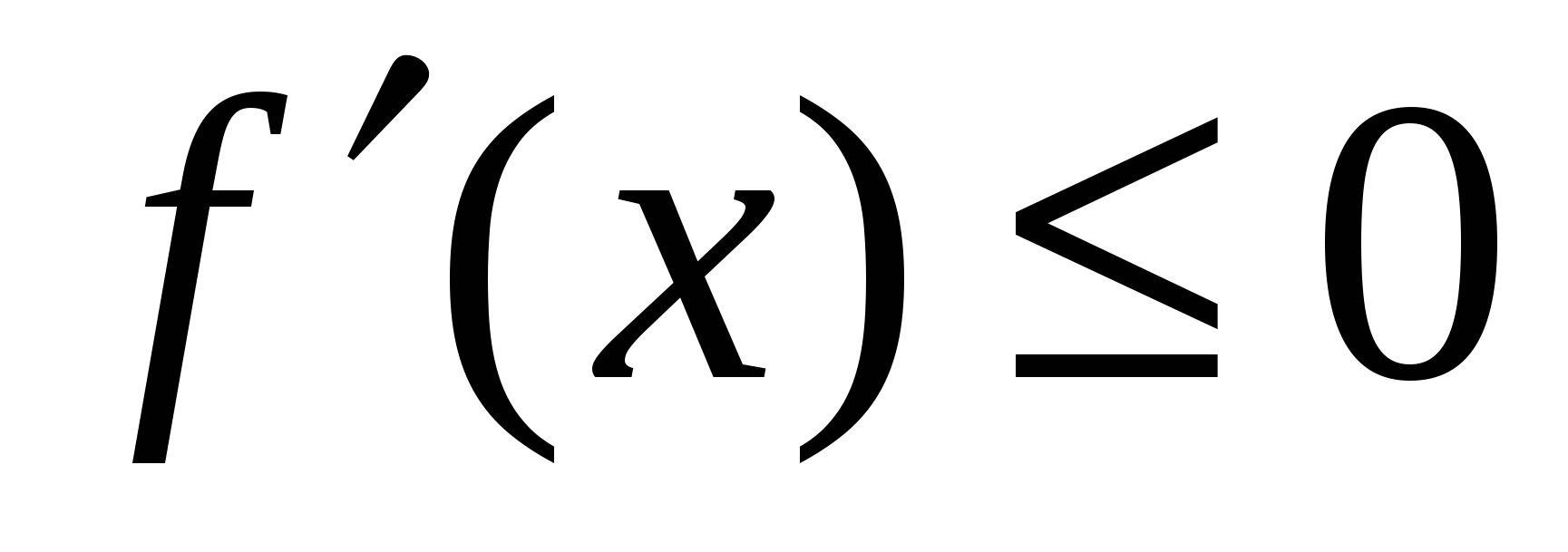 ) на интервале ) на интервале 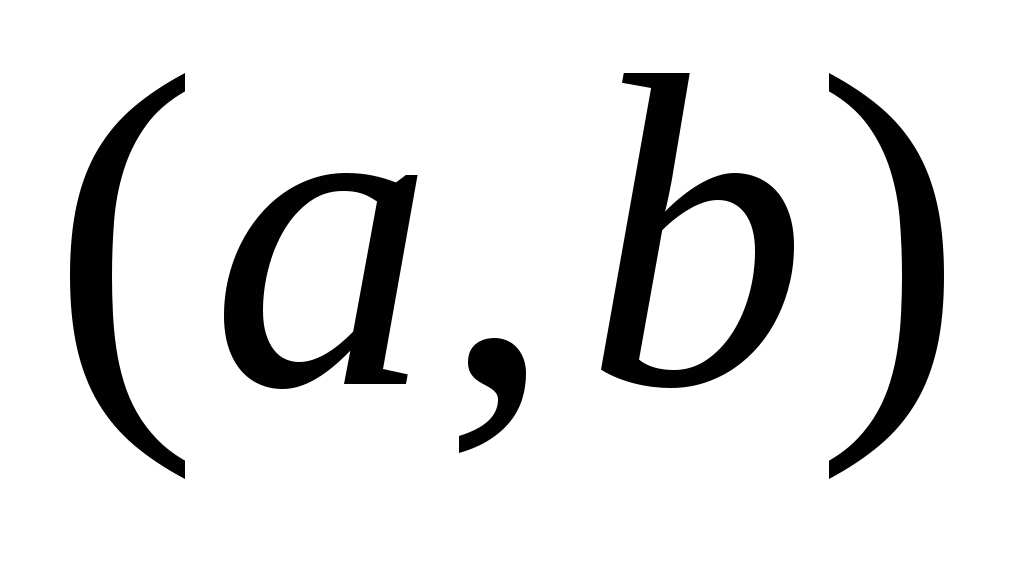 , то она не убывает (не возрастает) на этом интервале. , то она не убывает (не возрастает) на этом интервале.
Алгоритм нахождения интервалов монотонности функции  : :
Найти 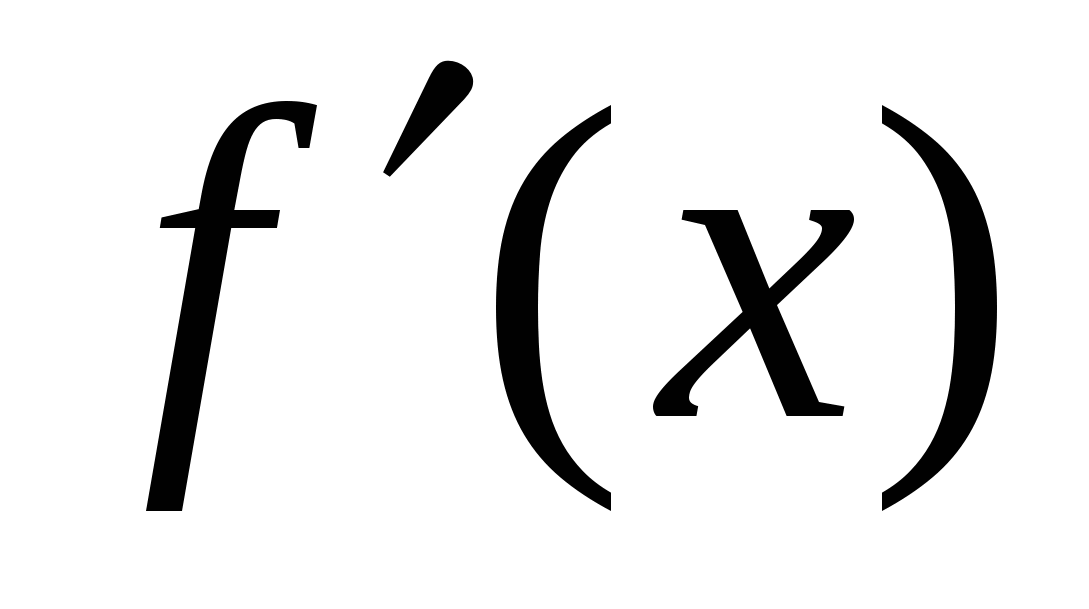 . .
Найти нули производной.
На числовой оси отметить область определения  , нули производной и те точки, где производная не существует. , нули производной и те точки, где производная не существует.
На каждом из полученных интервалов определить знак производной 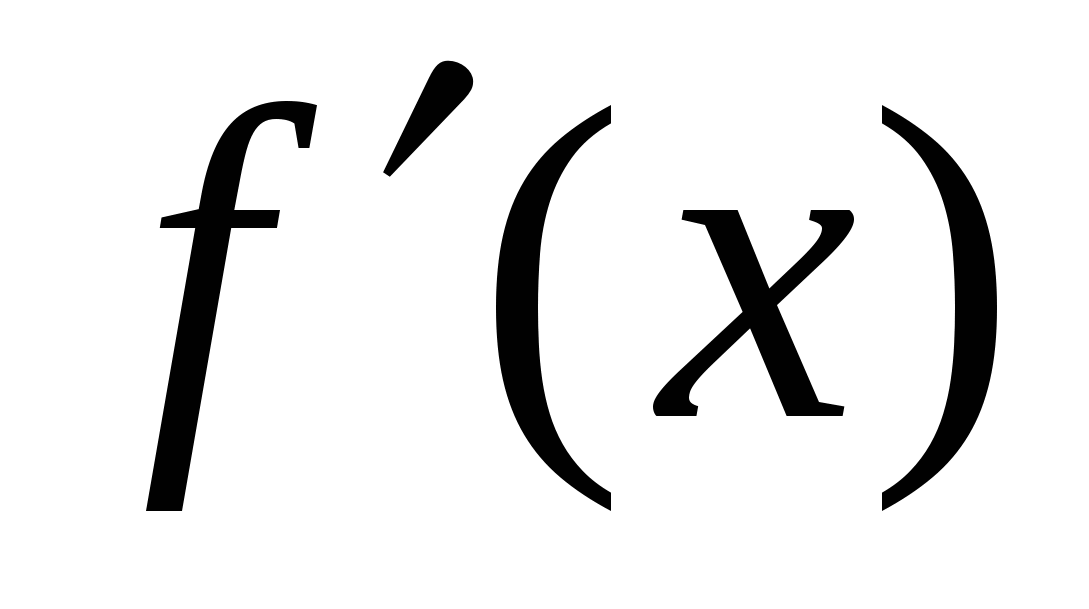 . .
Сделать вывод о возрастании или убывании функции  на каждом интервале. на каждом интервале.
Пример. Найти интервалы монотонности функции 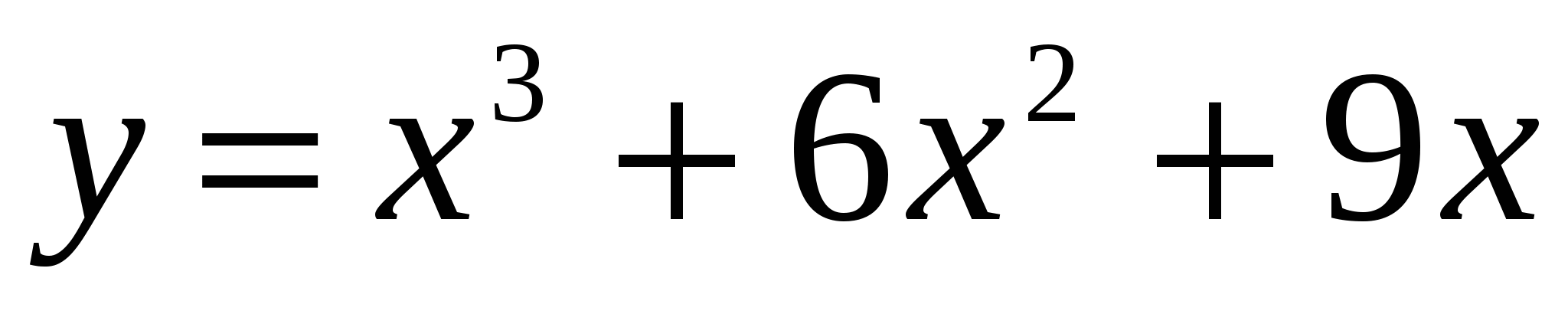 . .
Точка 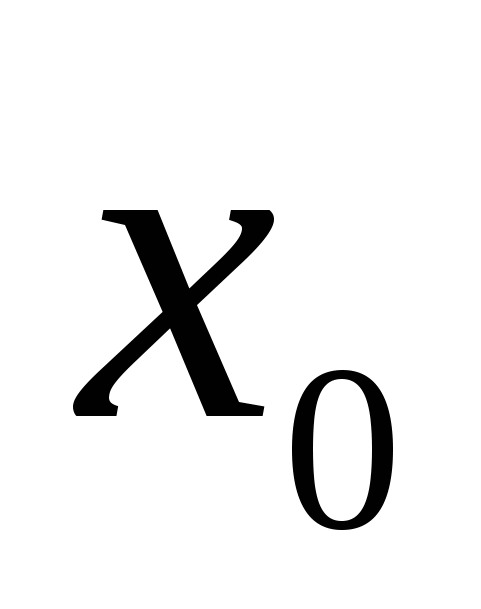 называется точкой максимума функции называется точкой максимума функции  , если существует некоторое число , если существует некоторое число 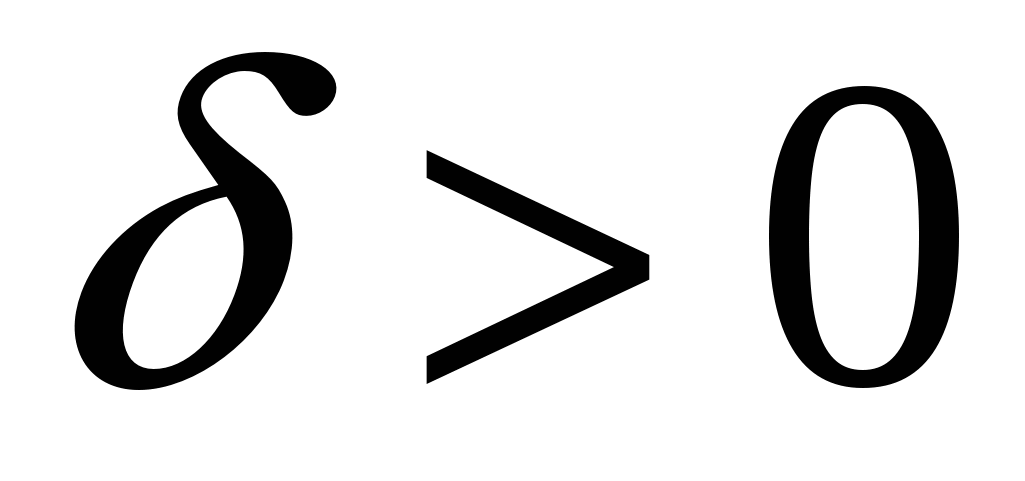 такое, что для всех такое, что для всех 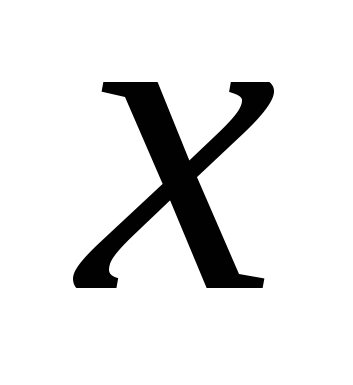 , удовлетворяющих условию , удовлетворяющих условию 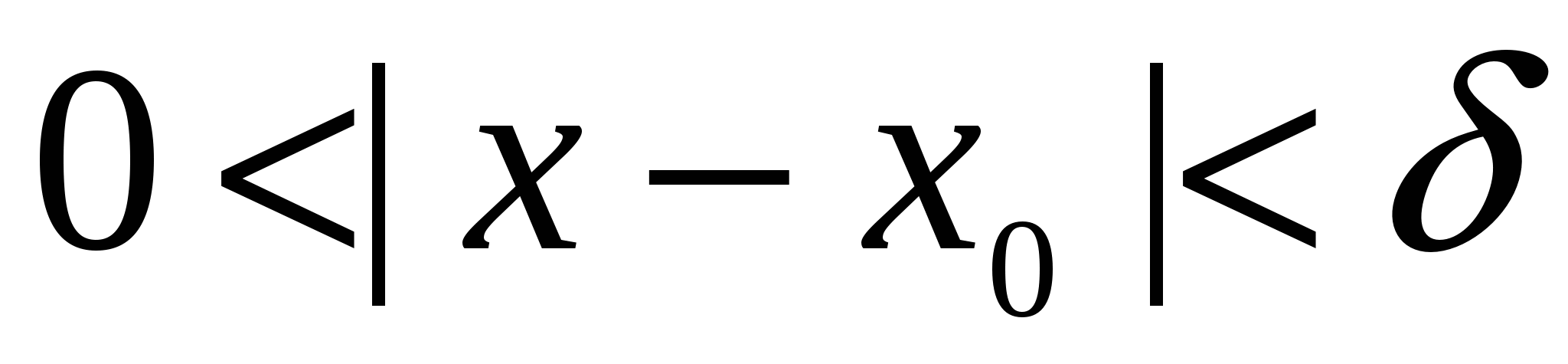 , выполнено неравенство , выполнено неравенство 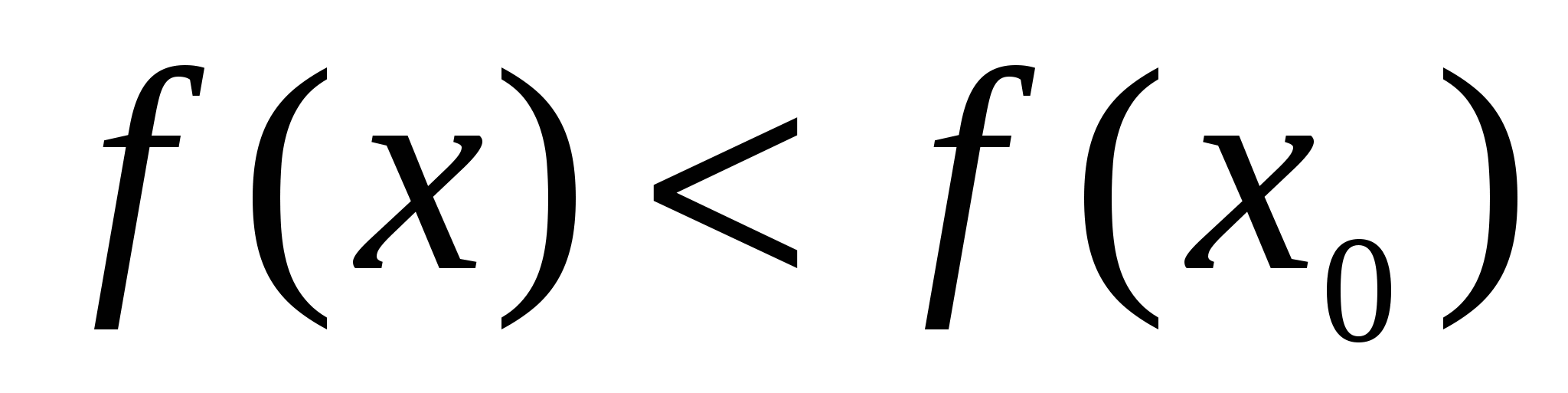 . .
Максимум функции – это значение функции в точке максимума.
На рис 2 показан пример графика функции, имеющей максимумы в точках 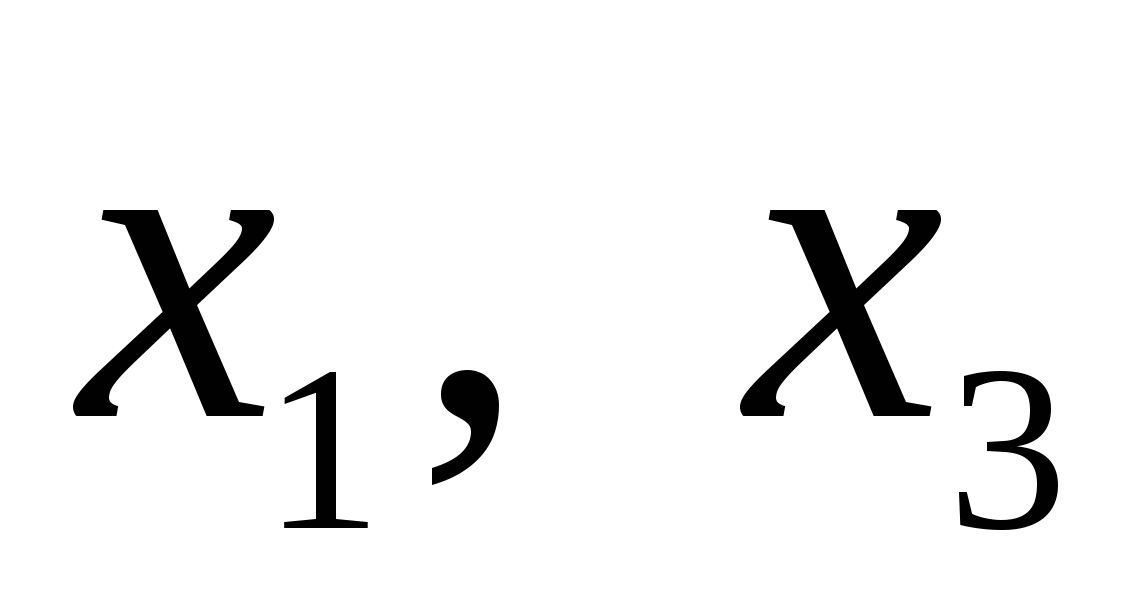 . .
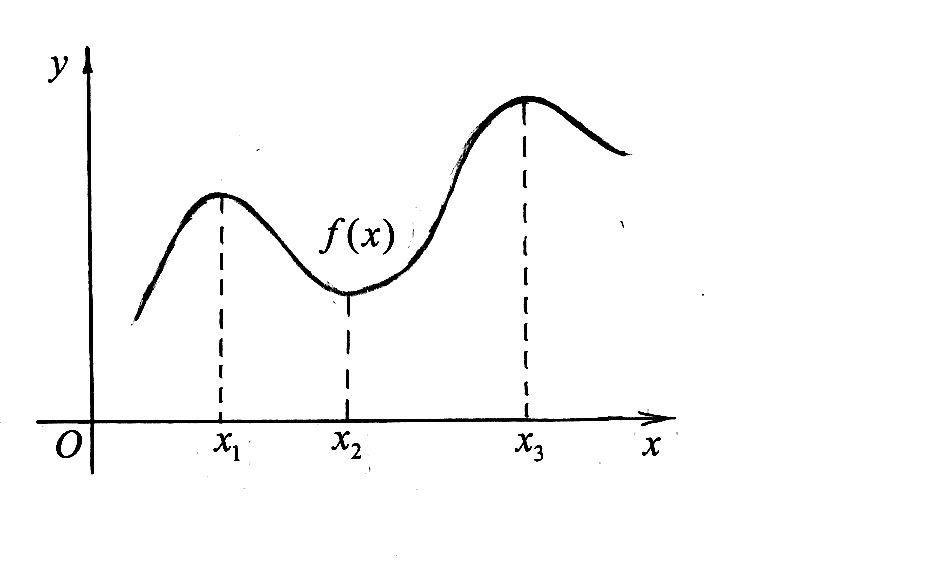
Рис. 2.
Точка 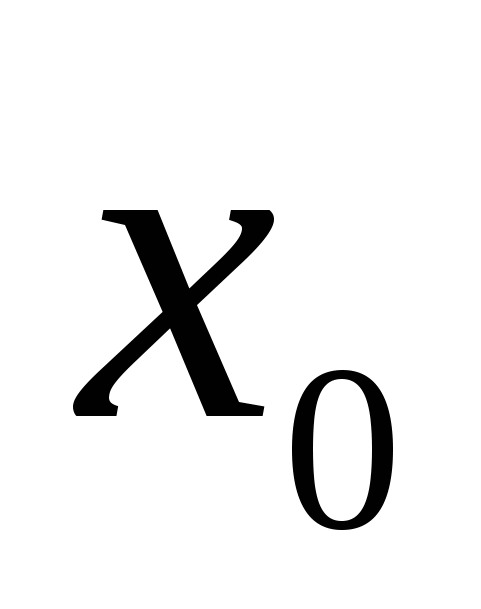 называется точкой минимума функции называется точкой минимума функции  , если существует некоторое число , если существует некоторое число 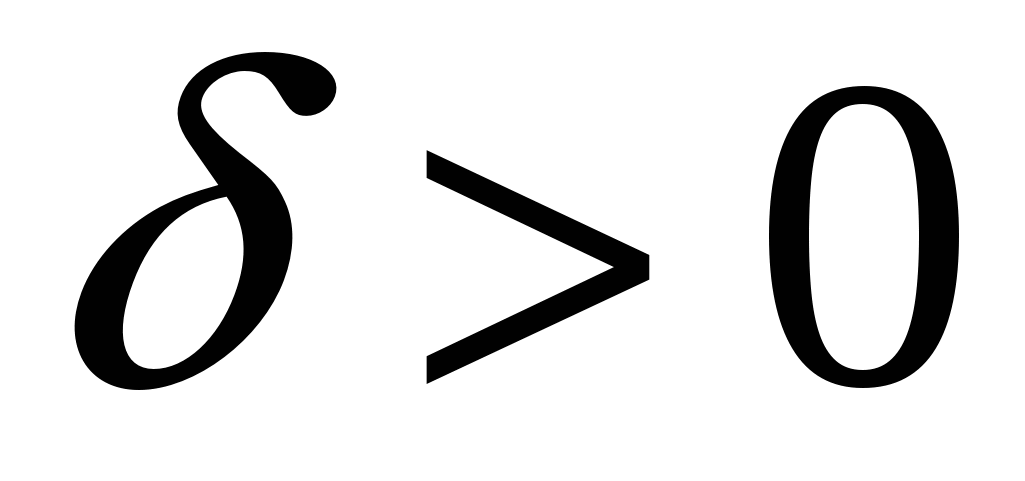 такое, что для всех такое, что для всех 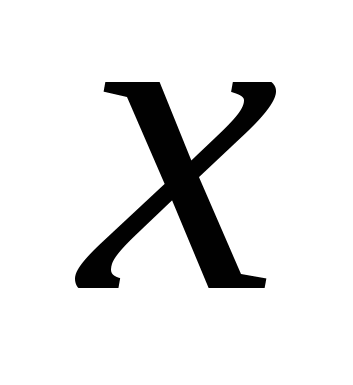 , удовлетворяющих условию , удовлетворяющих условию 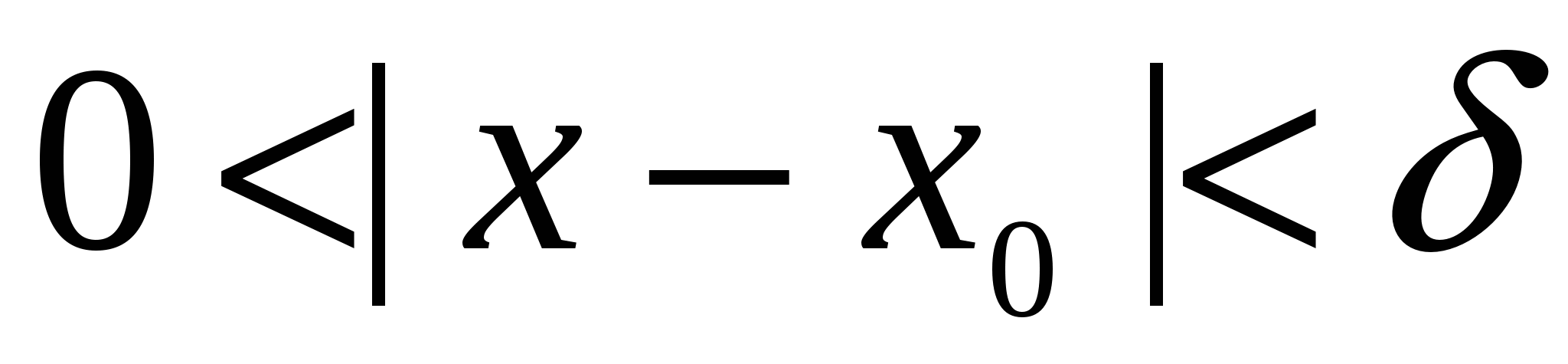 , выполнено неравенство , выполнено неравенство 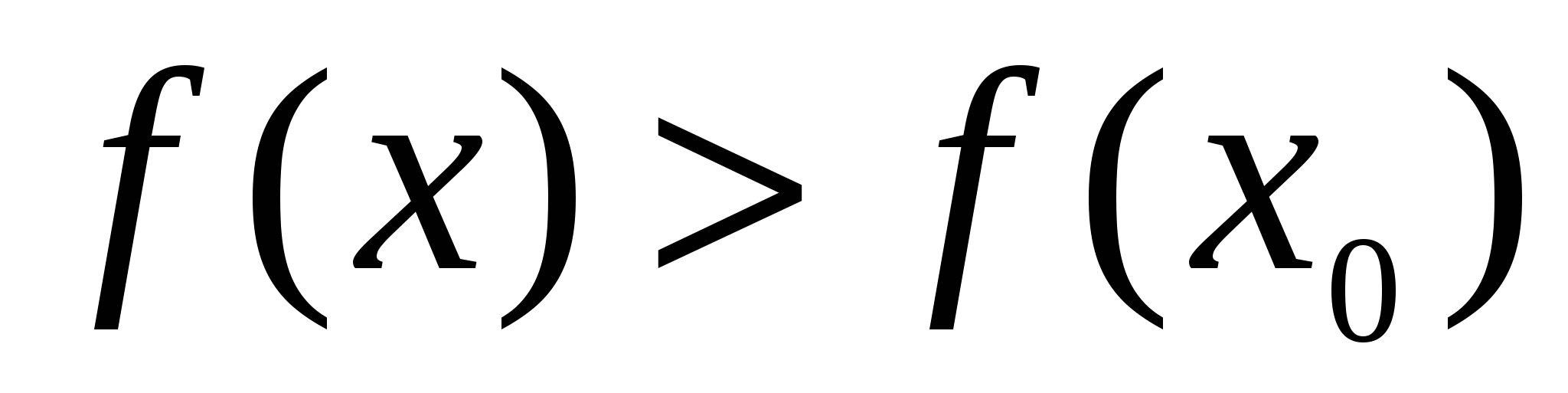 . На рис. 2 функция имеет минимум в точке . На рис. 2 функция имеет минимум в точке 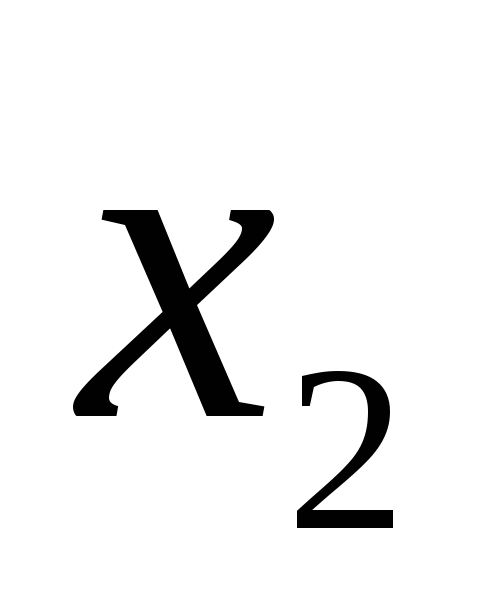 . .
Для максимумов и минимумов есть общее название – экстремумы. Соответственно точки максимума и точки минимума называются точками экстремума.
Функция, определенная на отрезке, может иметь максимум и минимум только в точках, находящихся внутри этого отрезка. Нельзя также путать максимум и минимум функции с ее наибольшим и наименьшим значением на отрезке – это понятия принципиально различные.
В точках экстремума у производной есть особые свойства.
Теорема (необходимое условие экстремума). Пусть в точке 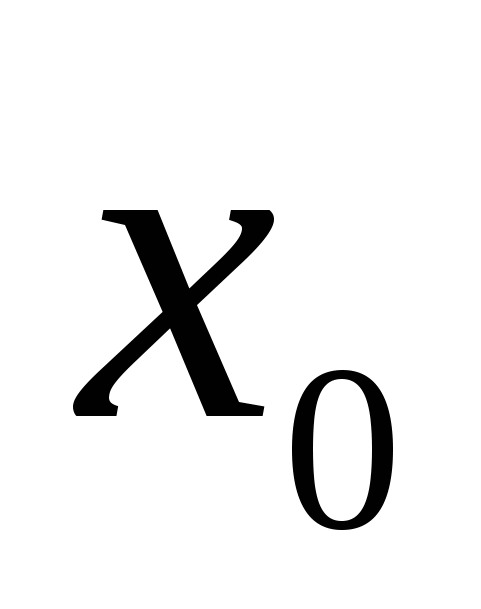 функция функция  имеет экстремум. Тогда либо имеет экстремум. Тогда либо 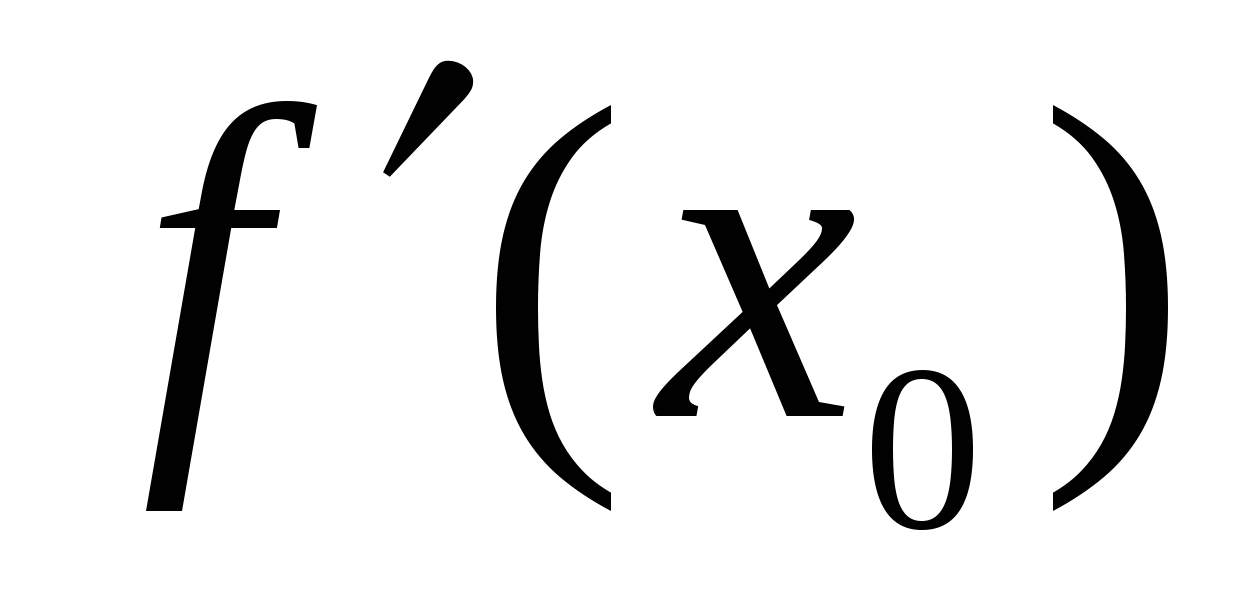 не существует, либо не существует, либо 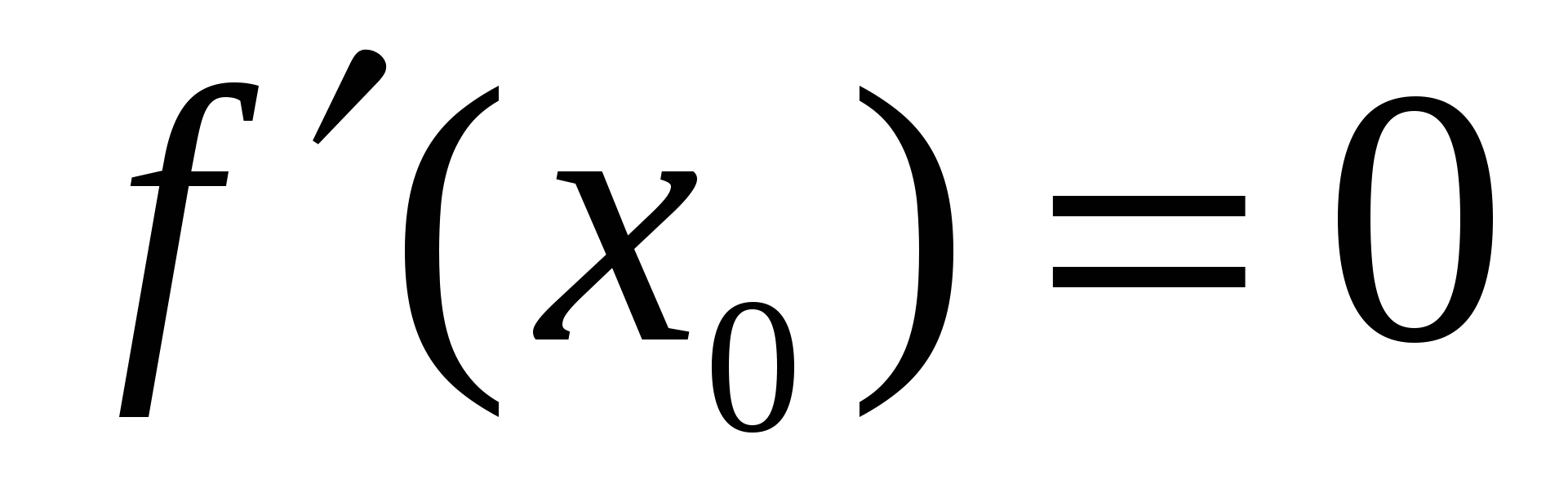 . .
Те точки из области определения функции, в которых 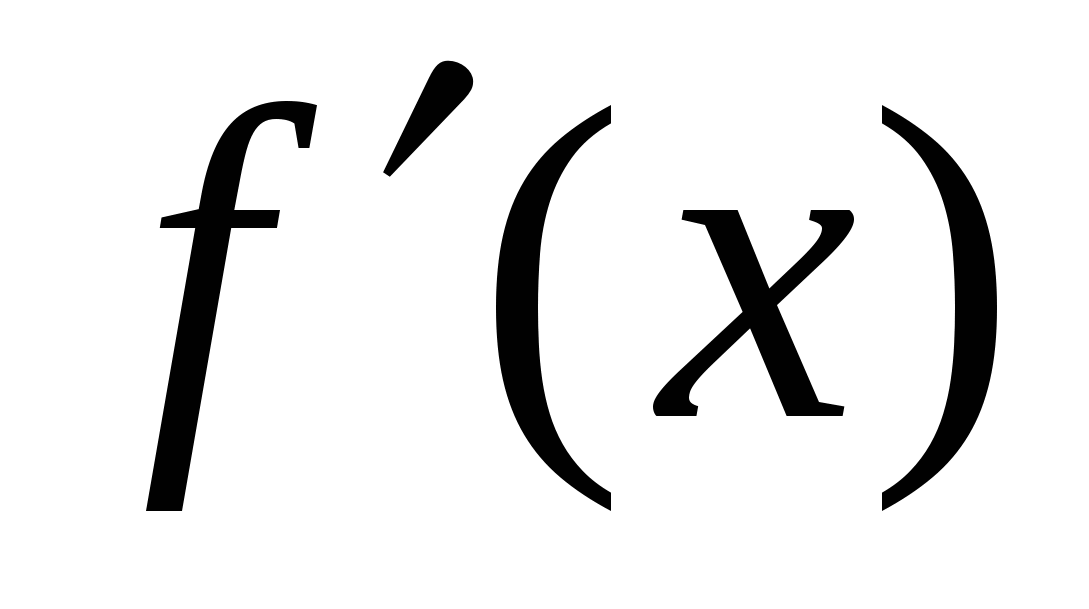 не существует или в которых не существует или в которых 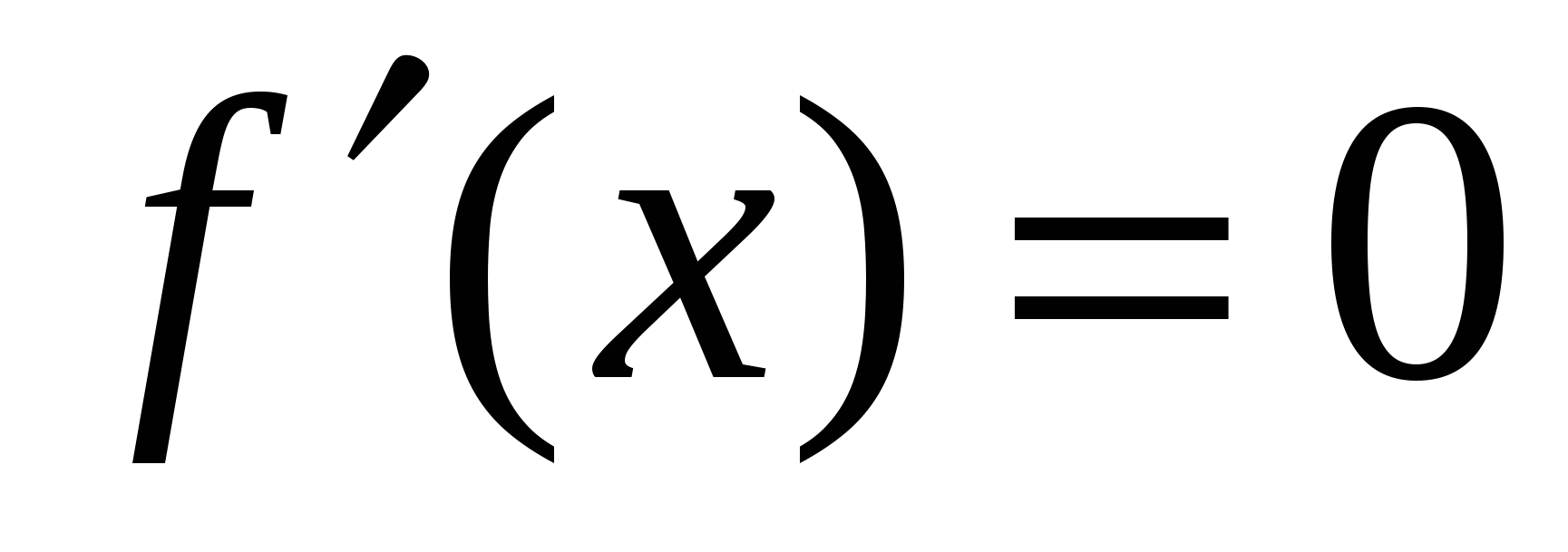 , называются критическими точками функции. , называются критическими точками функции.
Таким образом, точки экстремума лежат среди критических точек. В общем случае критическая точка не обязана быть точкой экстремума. Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум.
Пример. Рассмотрим 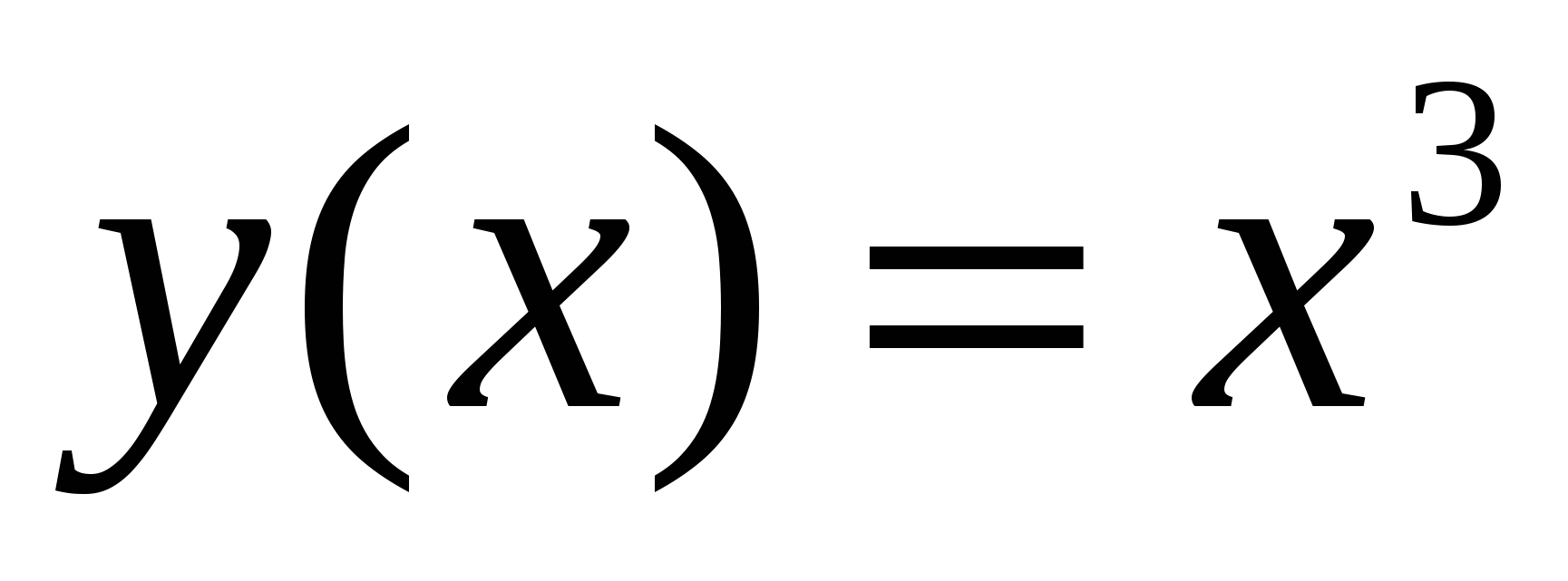 . Имеем . Имеем 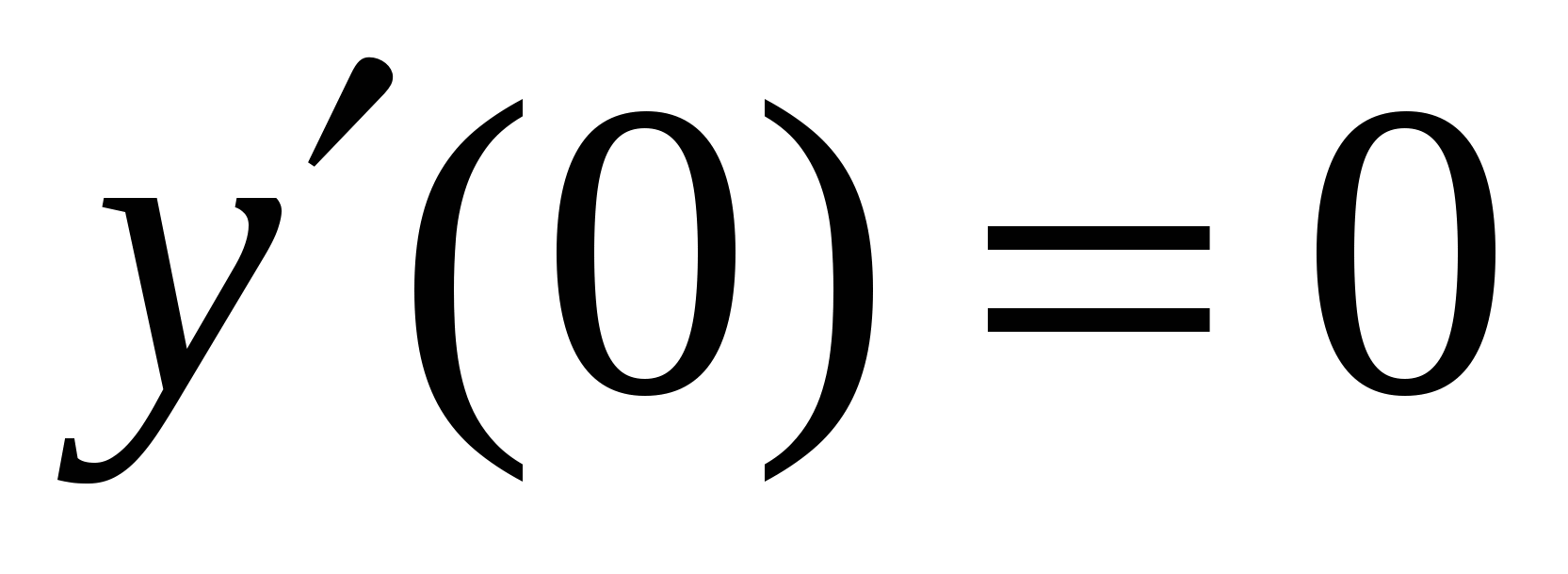 , но точка , но точка 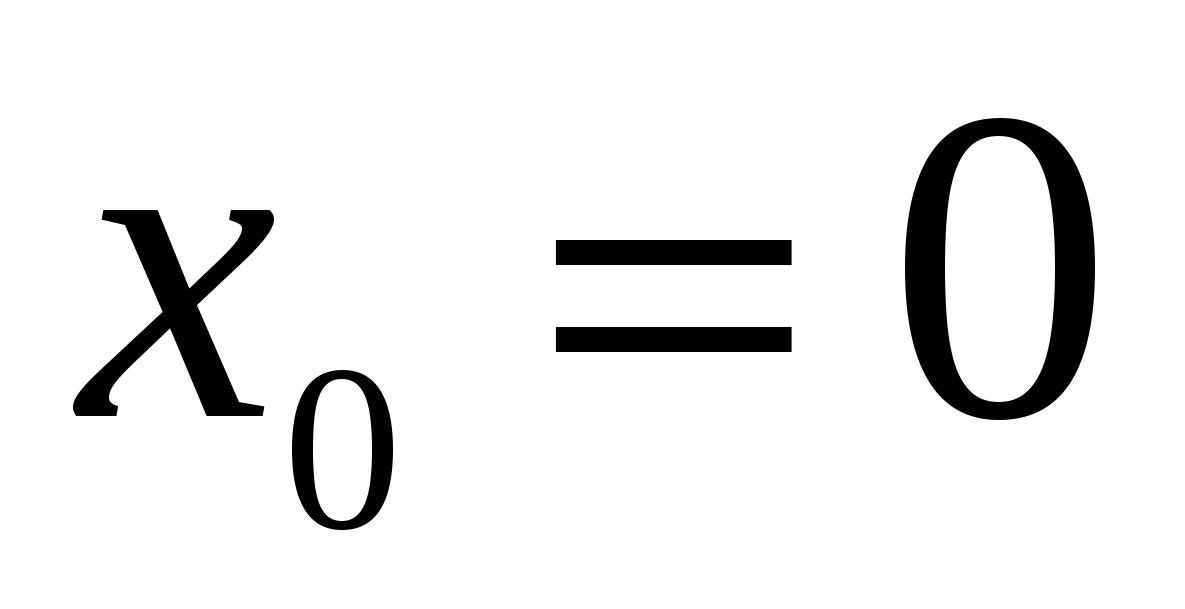 не является точкой экстремума (см. рис 3). не является точкой экстремума (см. рис 3).
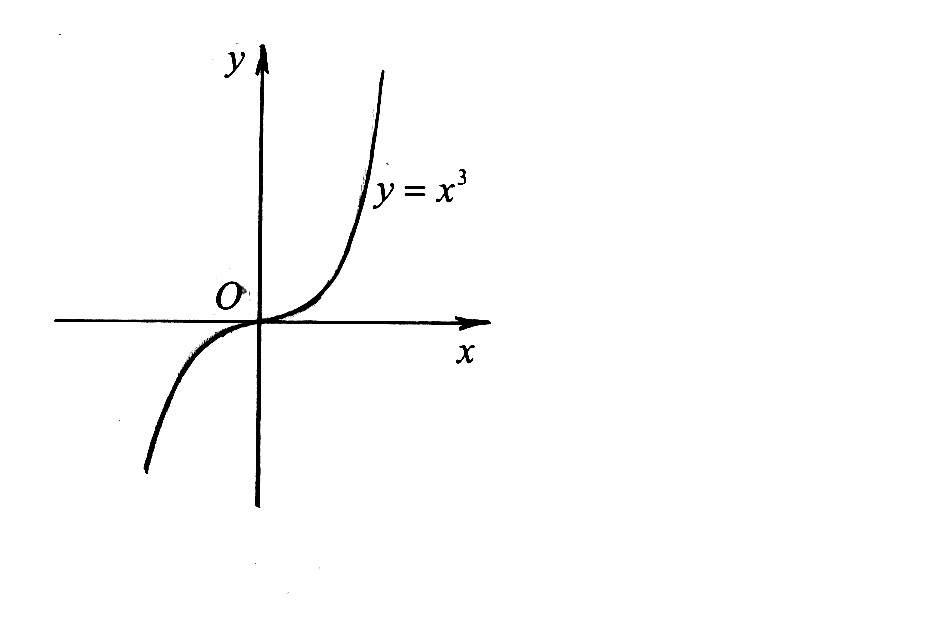
Рис. 3.
Теорема (первое достаточное условие экстремума). Пусть в точке 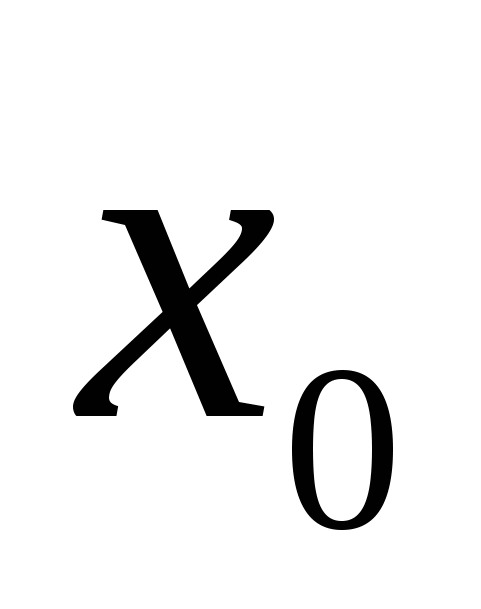 функция функция  непрерывна, а производная непрерывна, а производная 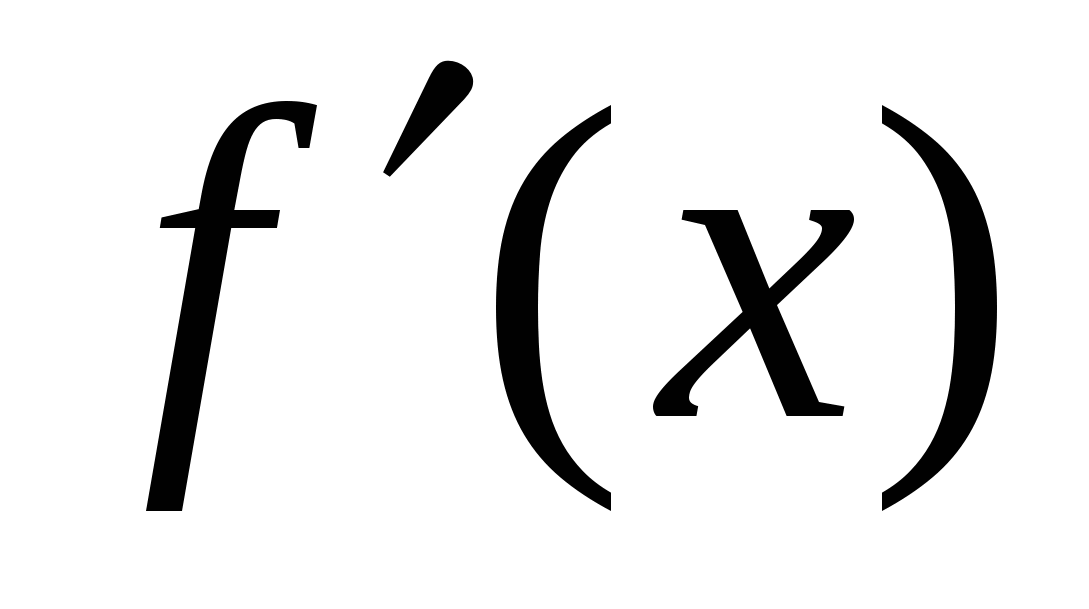 при переходе через точку при переходе через точку 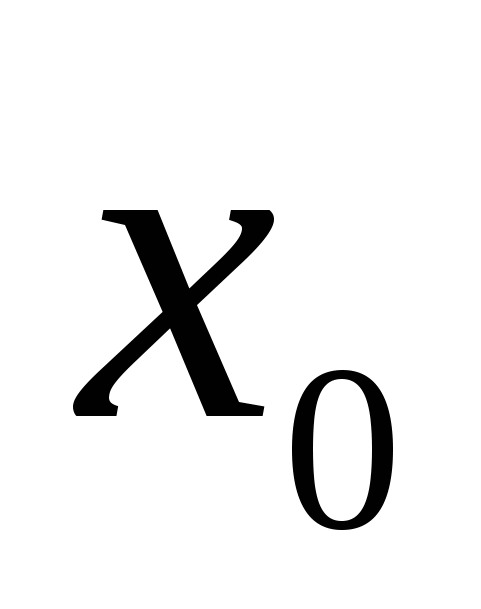 меняет знак. Тогда меняет знак. Тогда 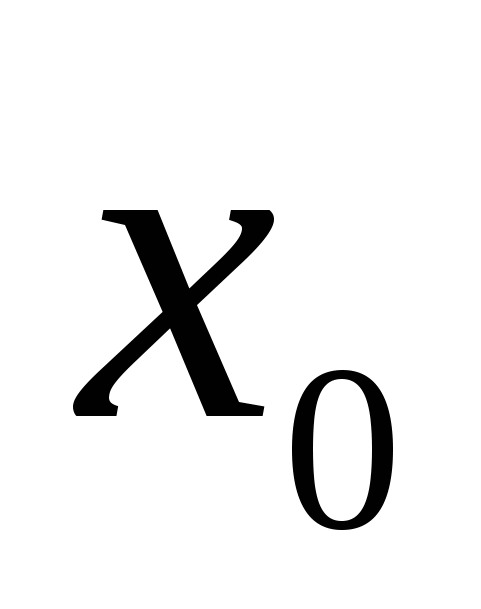 – точка экстремума: максимума, если знак меняется с «+» на «–», и минимума, если с «–» на «+». – точка экстремума: максимума, если знак меняется с «+» на «–», и минимума, если с «–» на «+».
Если при переходе через точку 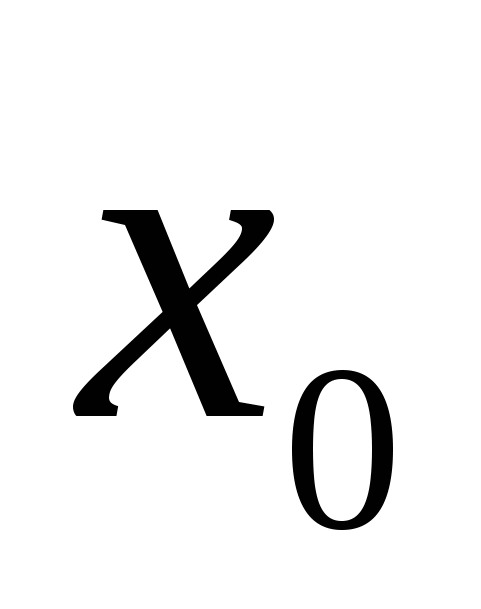 производная не меняет знак, то в точке производная не меняет знак, то в точке 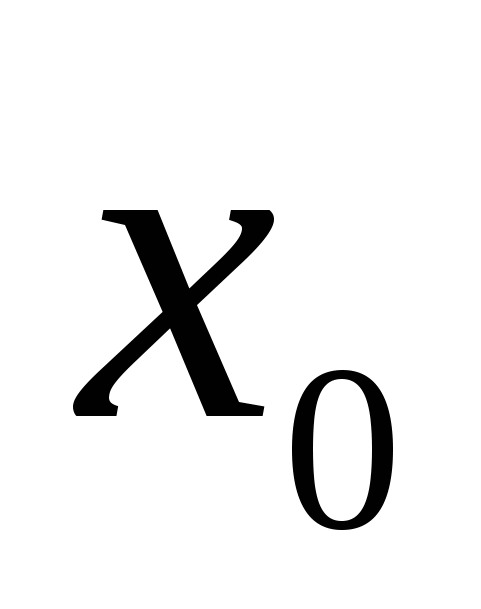 экстремума нет. экстремума нет.
Теорема (второе достаточное условие экстремума). Пусть в точке 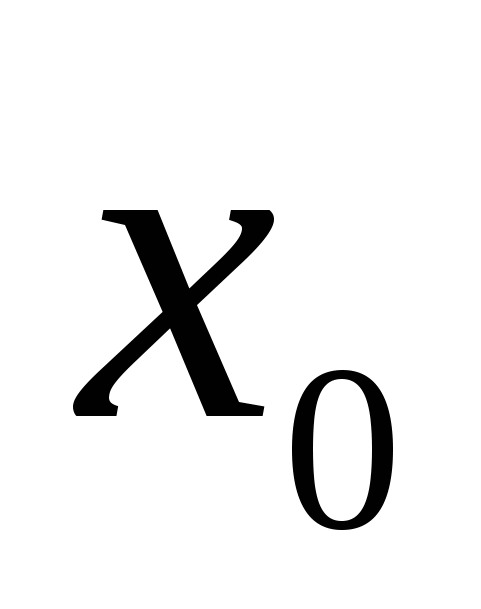 производная дважды дифференцируемой функции производная дважды дифференцируемой функции  равна нулю ( равна нулю (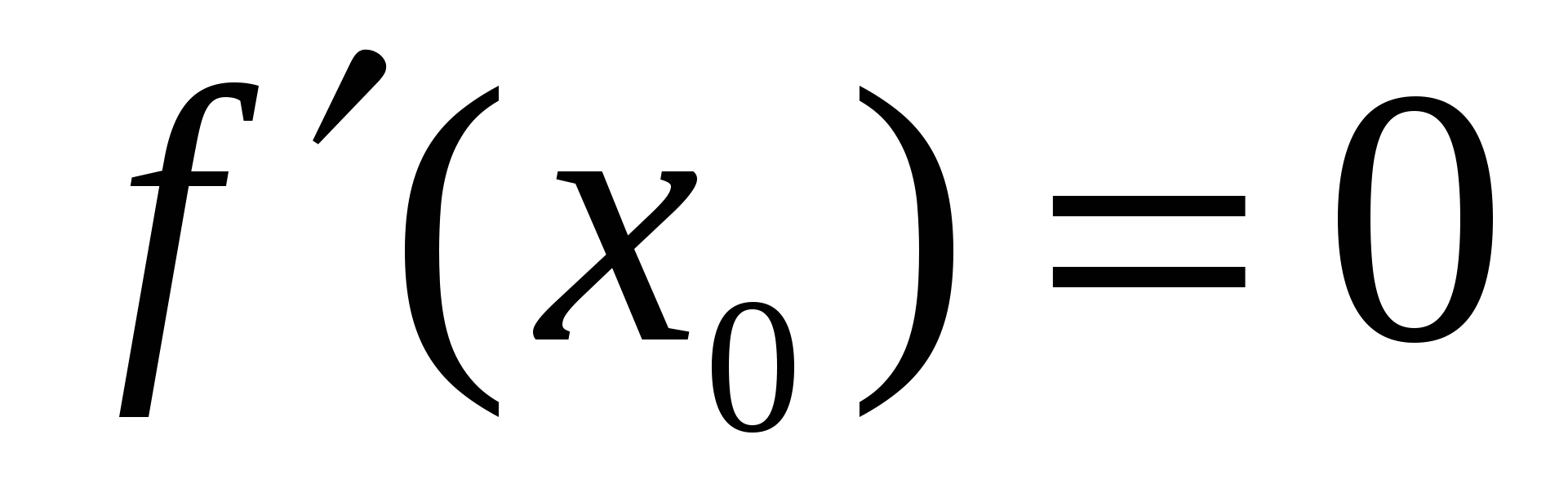 ), а ее вторая производная в этой точке отлична от нуля ( ), а ее вторая производная в этой точке отлична от нуля (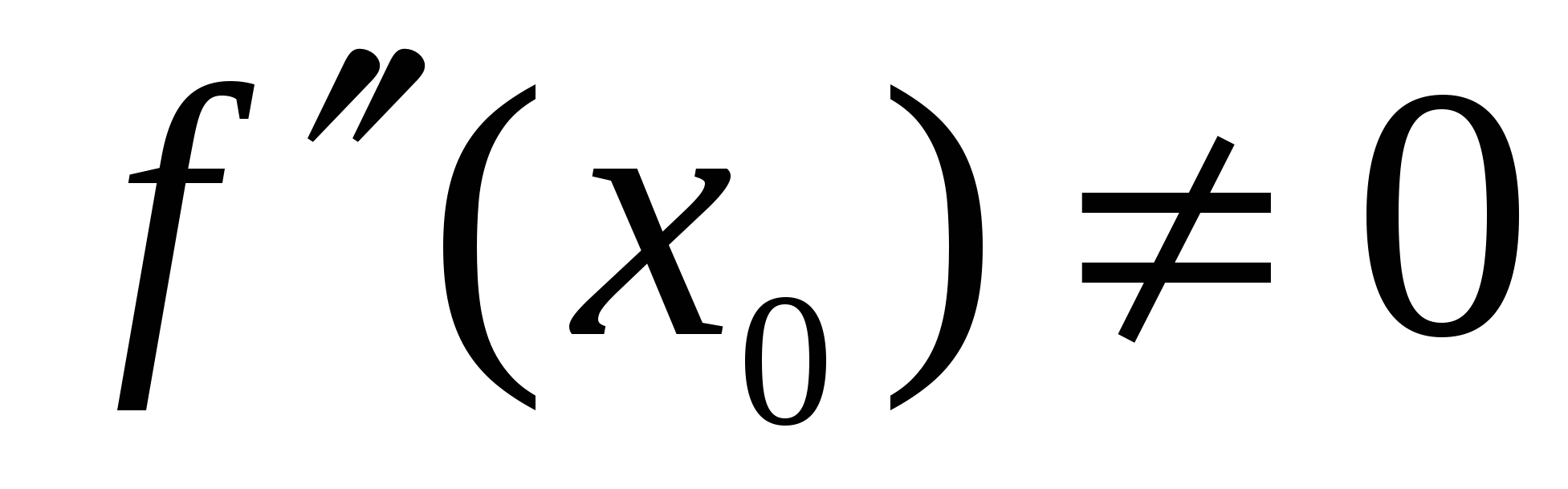 ) и непрерывна в некоторой окрестности точки ) и непрерывна в некоторой окрестности точки 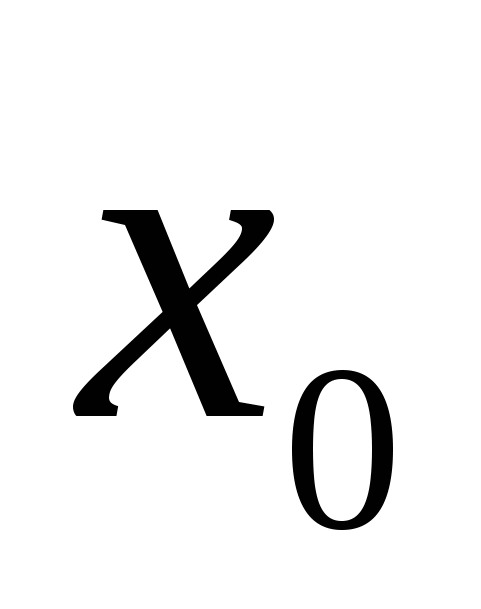 . Тогда . Тогда 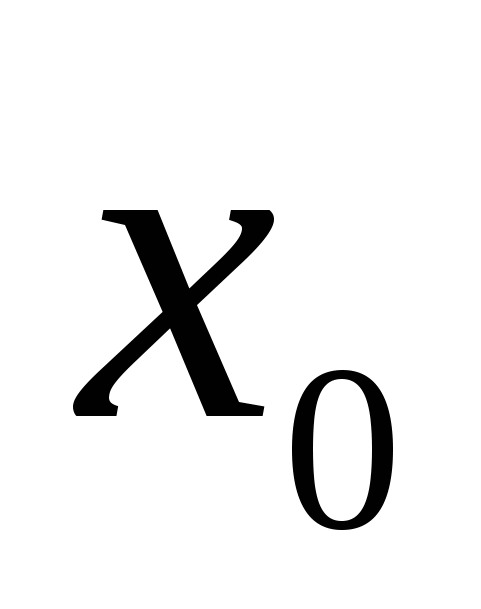 – точка экстремума – точка экстремума  ; при ; при 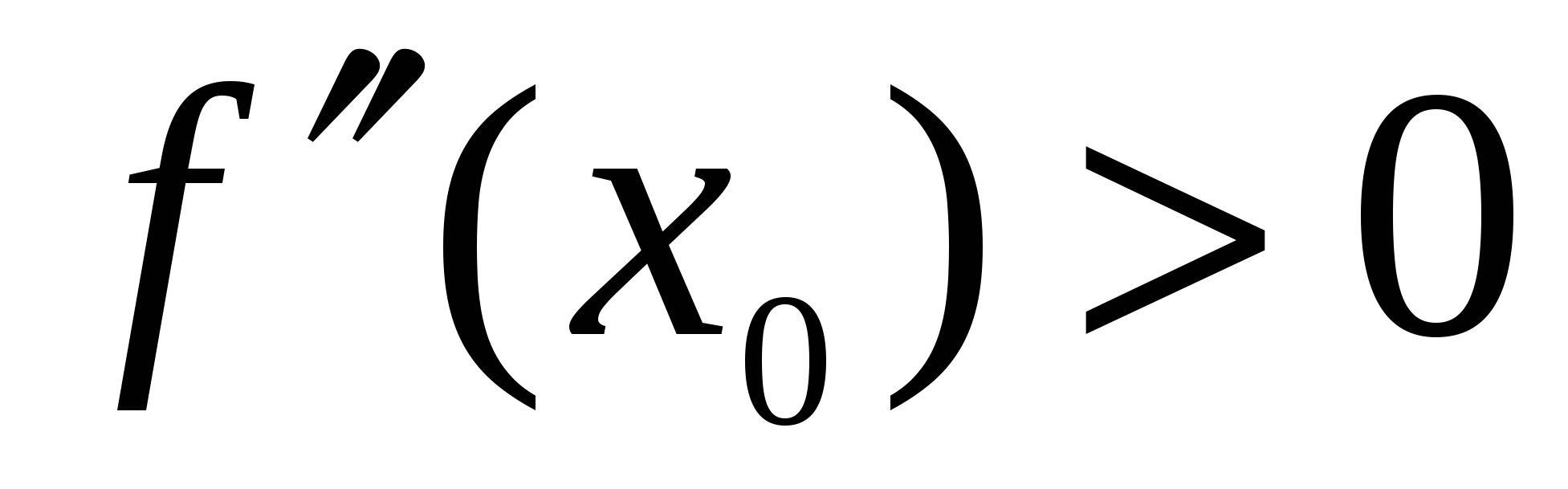 это точка минимума, а при это точка минимума, а при 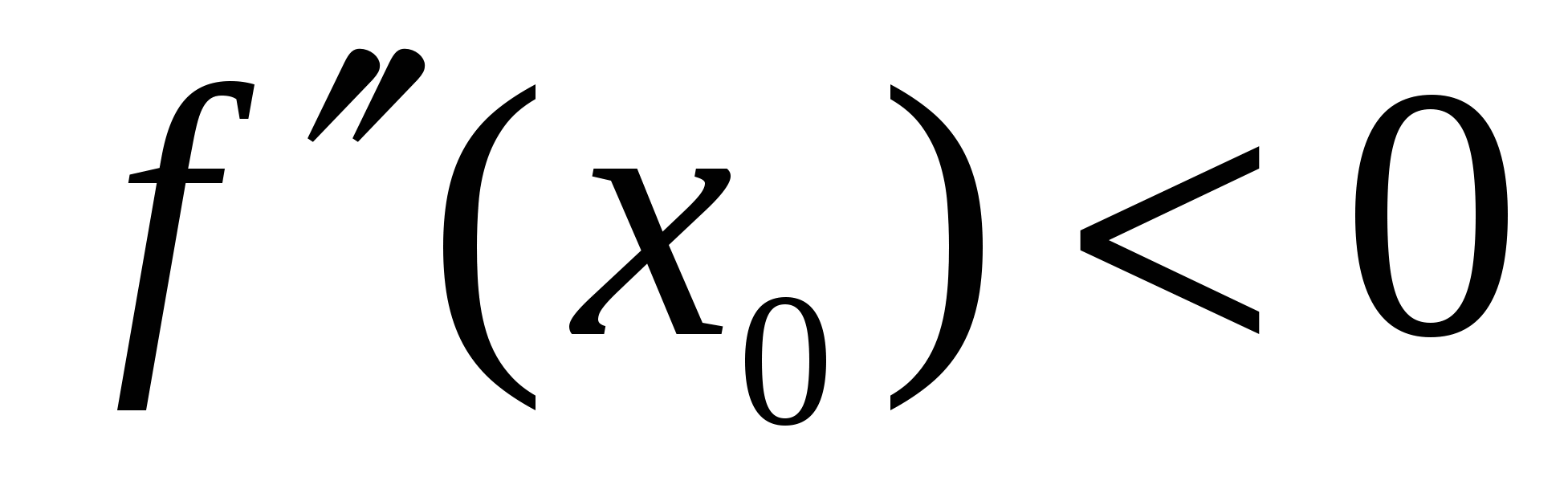 это точка максимума. это точка максимума.
Алгоритм нахождения экстремумов функции с помощью первого достаточного условия экстремума:
Найти производную.
Найти критические точки функции.
Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов.
Найти экстремальные значения функции.
Алгоритм нахождения экстремумов функции с помощью второго достаточного условия экстремума:
Найти производную 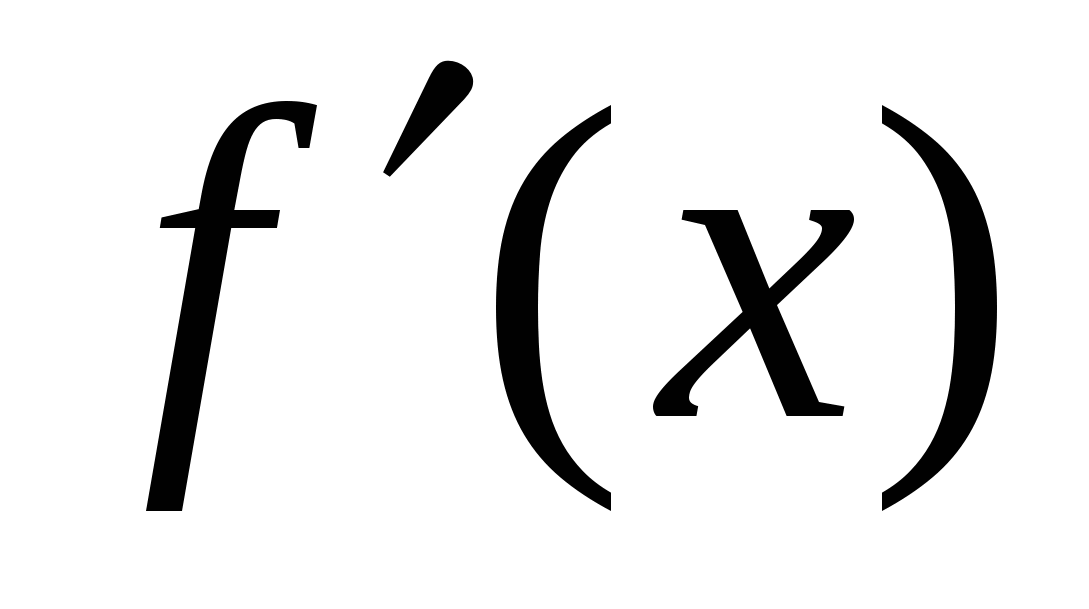 . .
Найти вторую производную 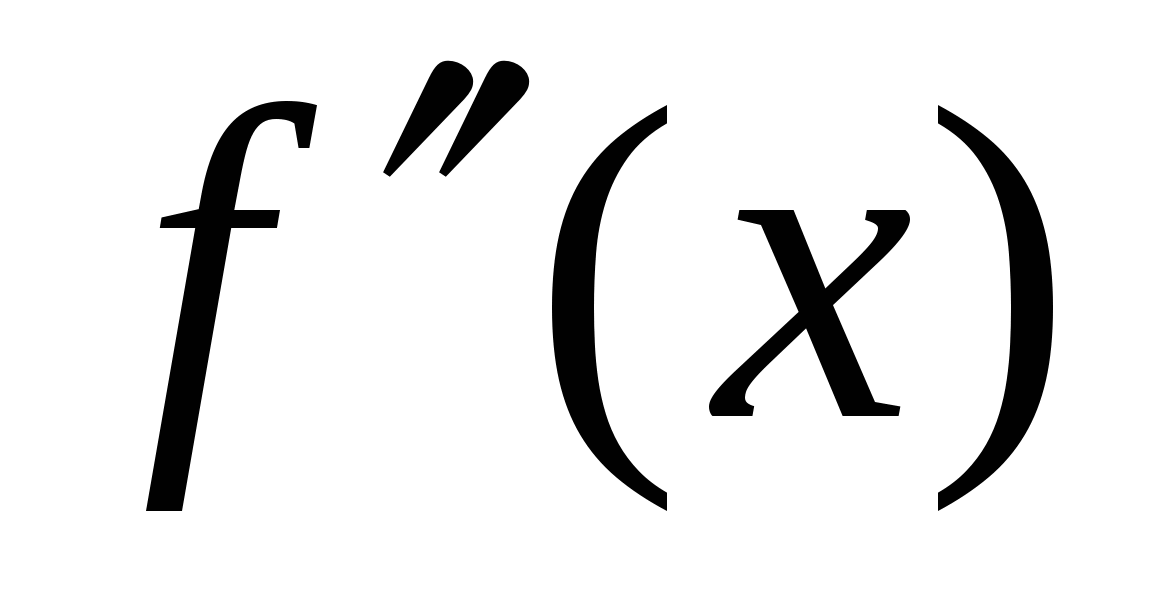 . .
Найти те точки, в которых 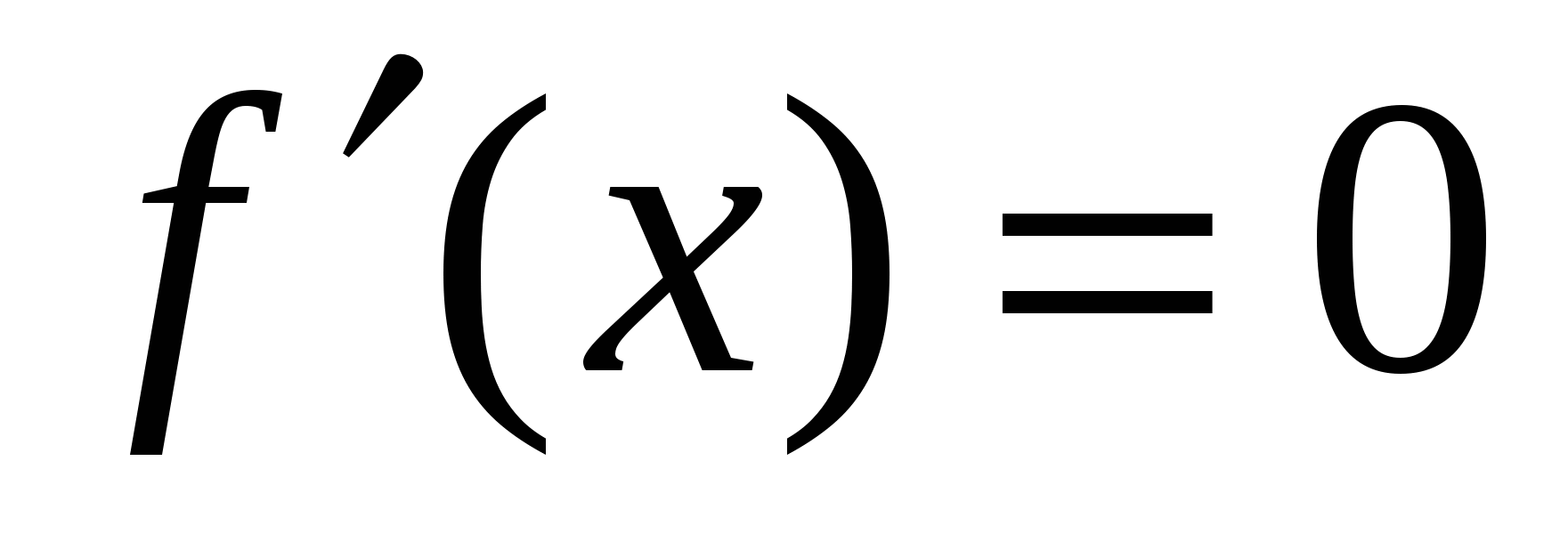 . .
В этих точках определить знак 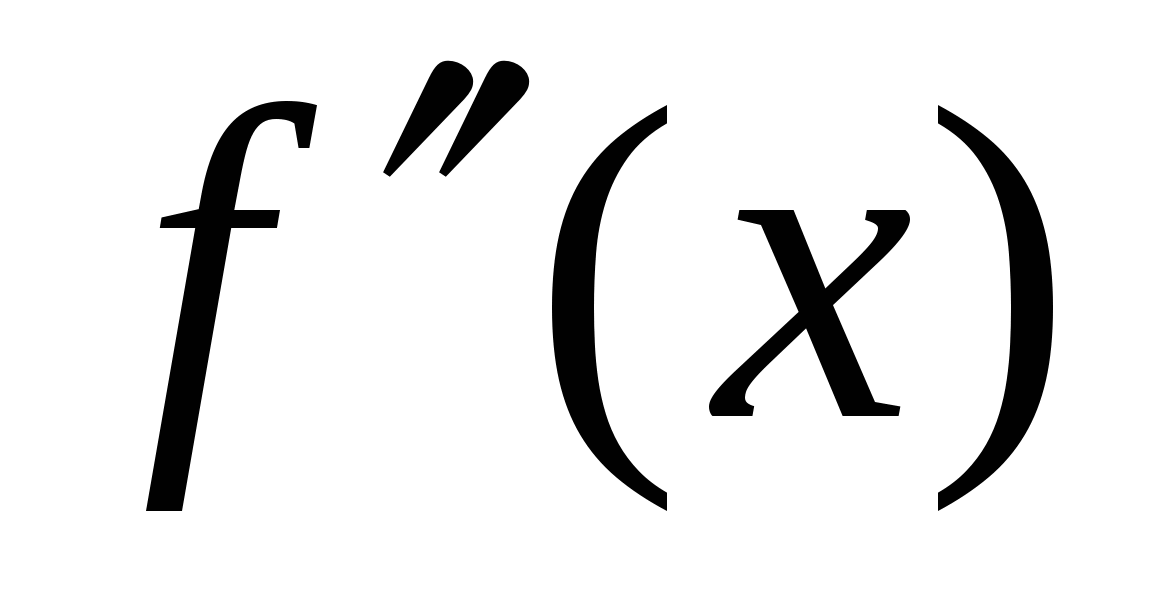 . .
Сделать вывод о существовании и характере экстремумов.
Найти экстремальные значения функции.
Пример. Найти экстремумы функции 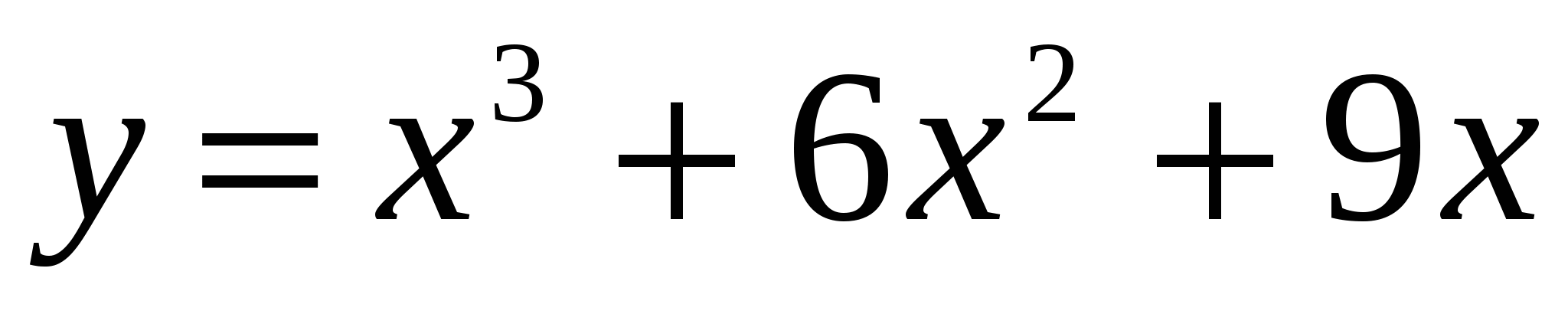 . .
Интервалы выпуклости и точки перегиба.
Функция  называется выпуклой вниз (выпуклой вверх) на промежутке называется выпуклой вниз (выпуклой вверх) на промежутке 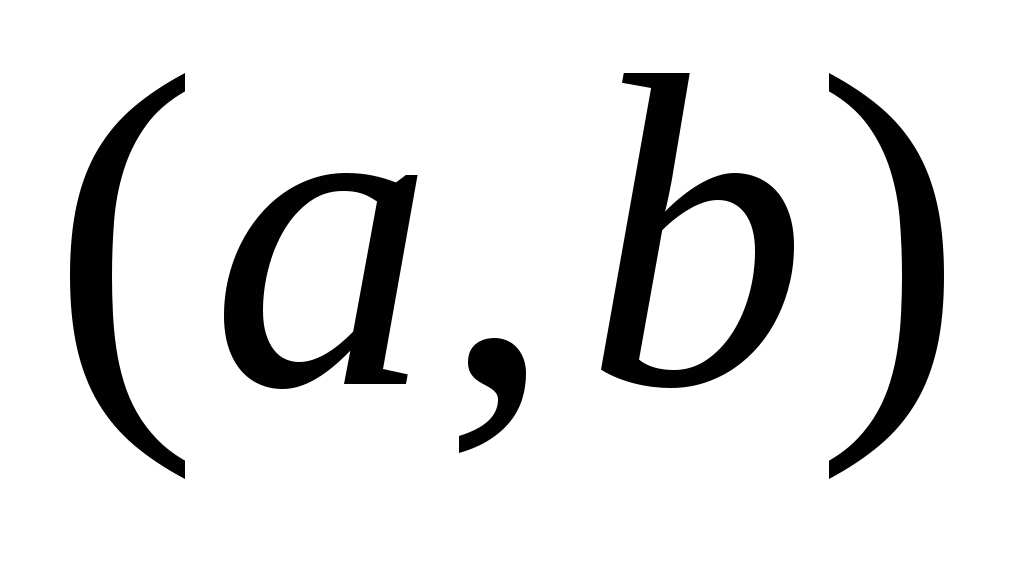 , если для любых значений , если для любых значений 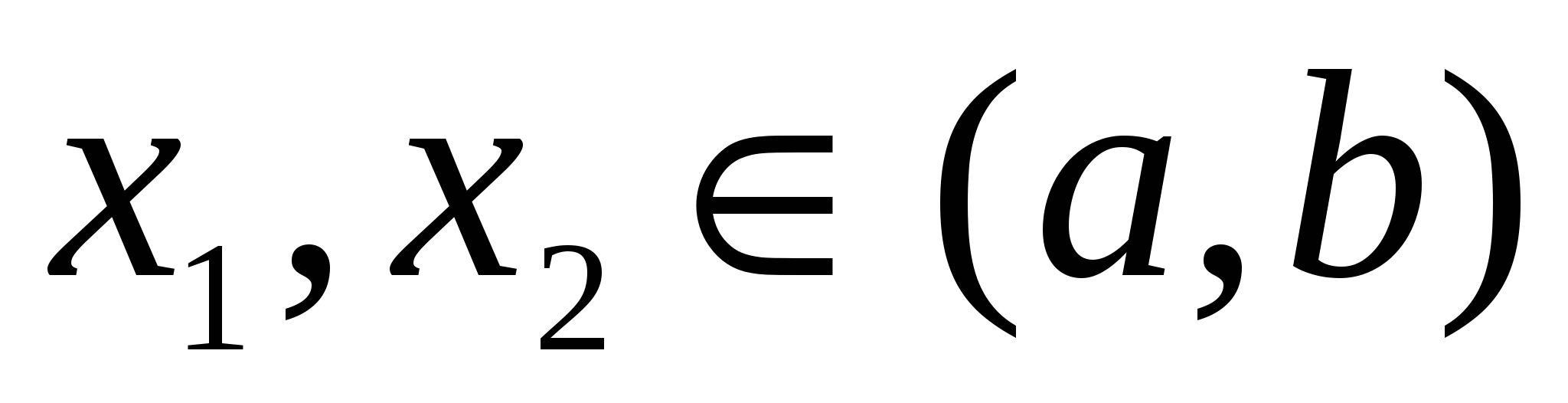 выполняется неравенство выполняется неравенство 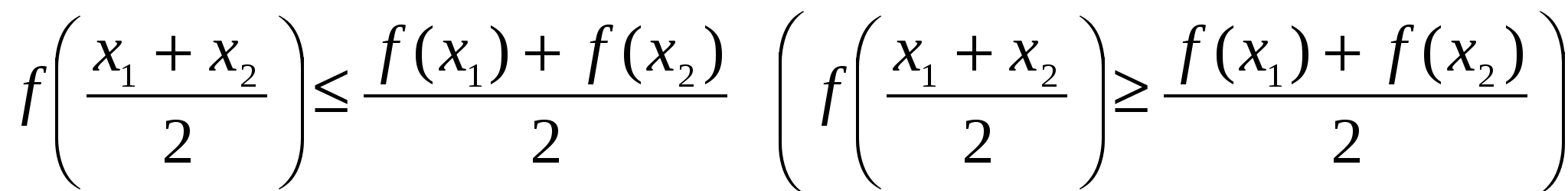 . .
Теорема (достаточное условие выпуклости функции). Если функция  имеет на интервале имеет на интервале 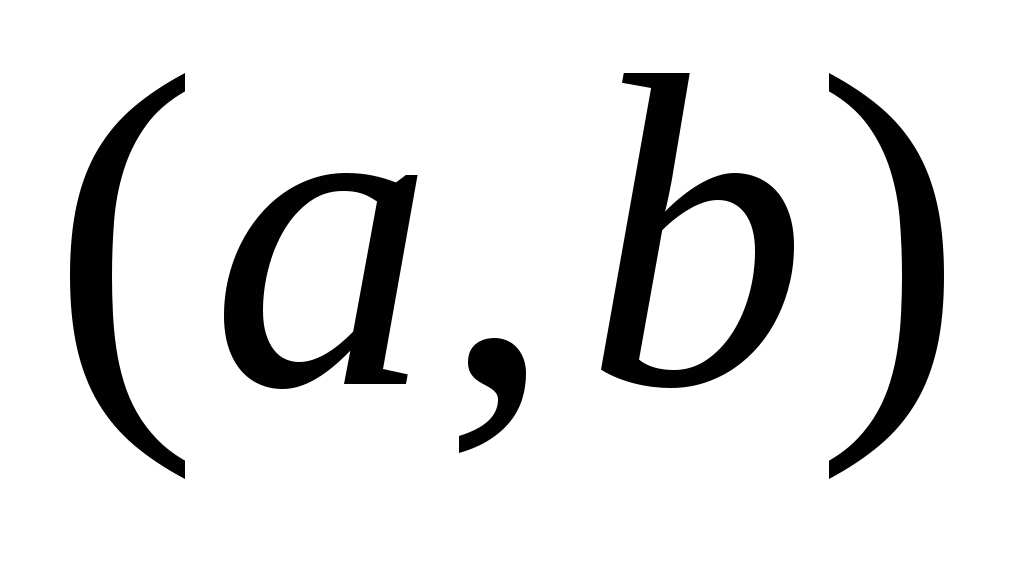 вторую производную вторую производную 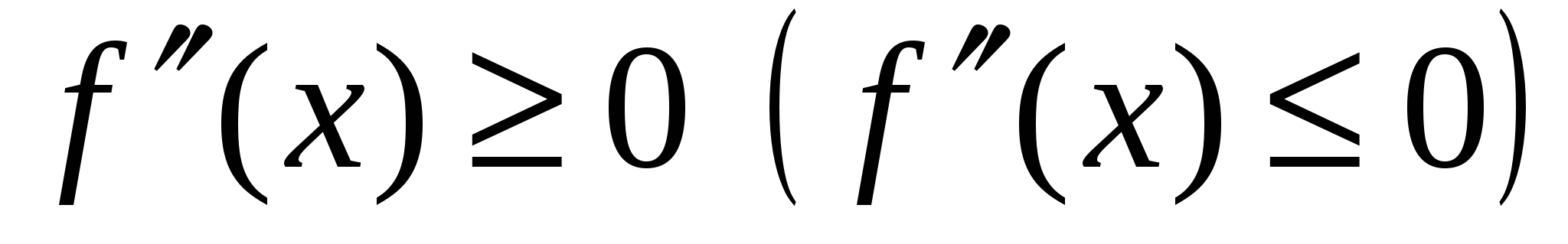 , то график функции имеет на , то график функции имеет на 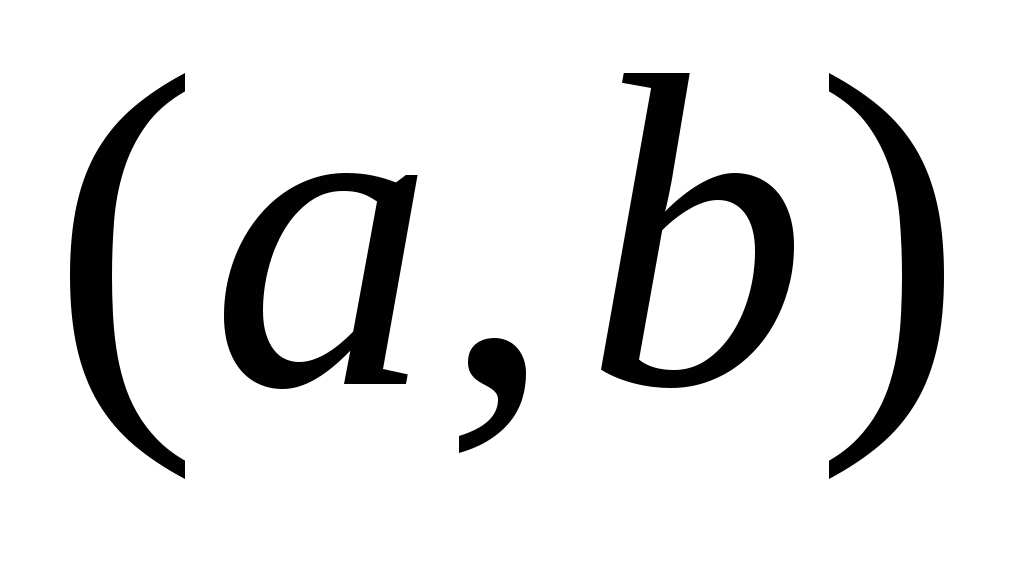 выпуклость направленную вниз (вверх). выпуклость направленную вниз (вверх).
Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла вниз и вверх.
Теорема (необходимое условие перегиба). Вторая производная дважды дифференцируемой функции  в точке перегиба в точке перегиба 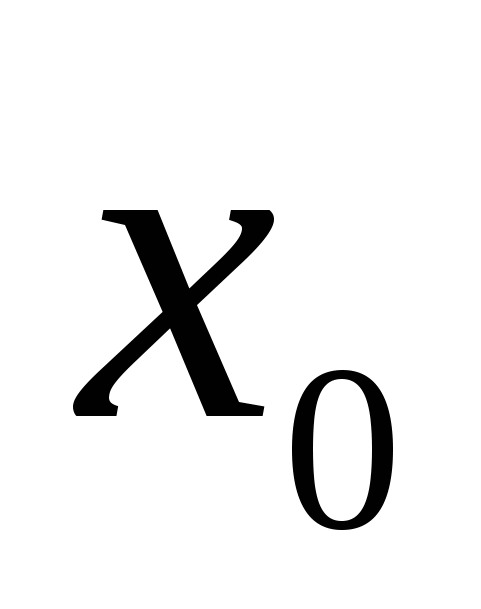 равна нулю, т.е. равна нулю, т.е. 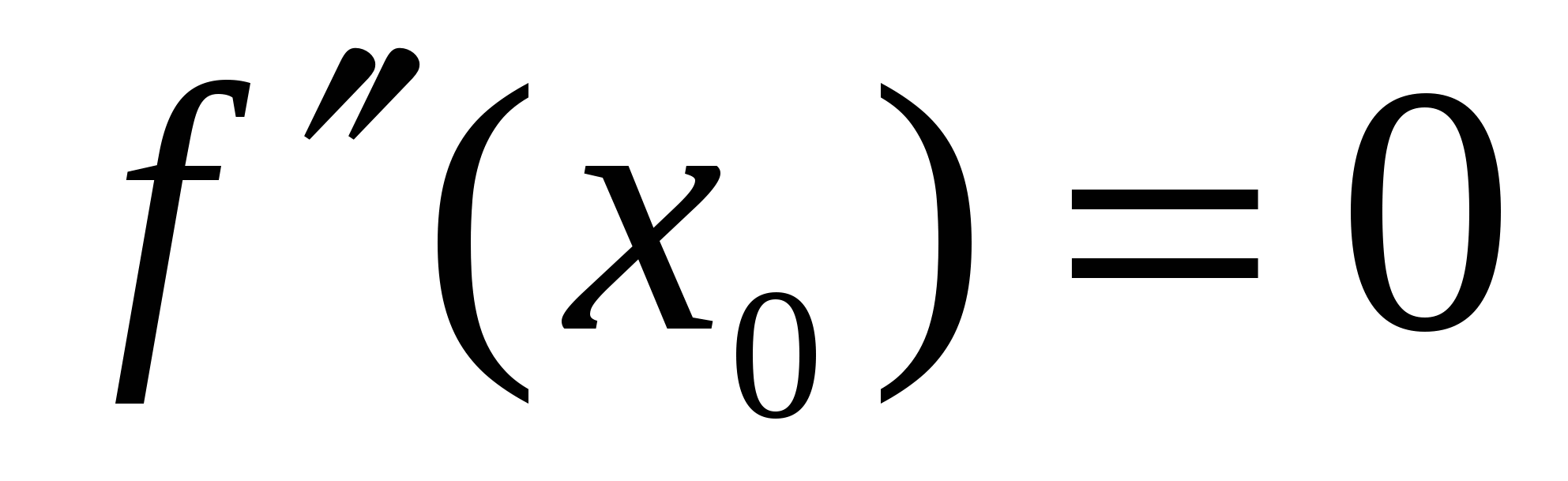 . .
Теорема (достаточное условие перегиба). Если вторая производная 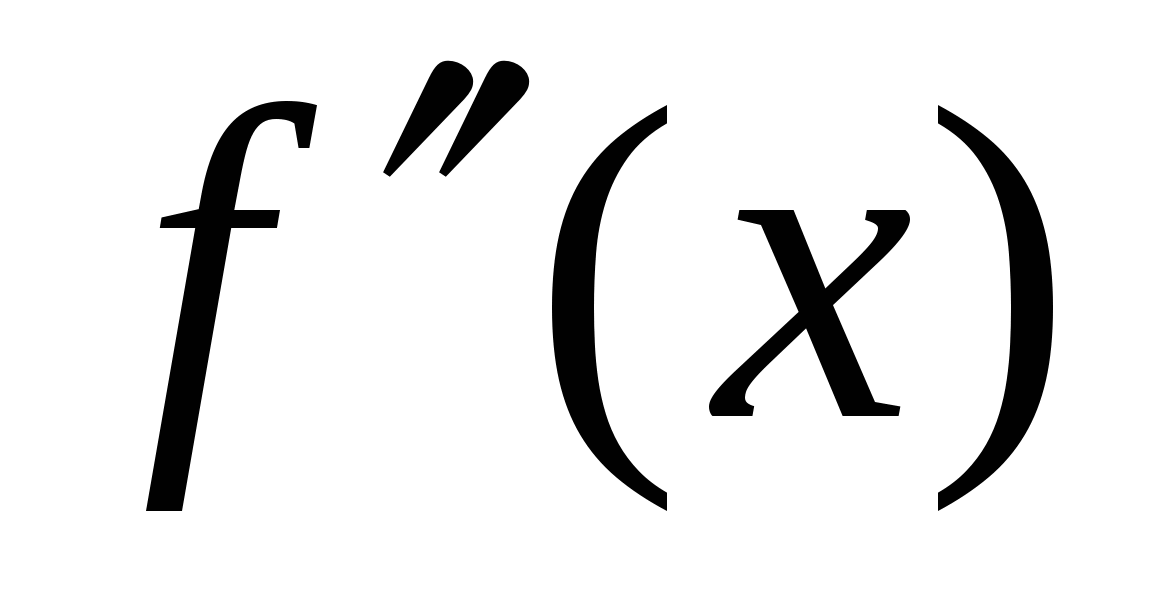 дважды дифференцируемой функции дважды дифференцируемой функции  при переходе через некоторую точку при переходе через некоторую точку 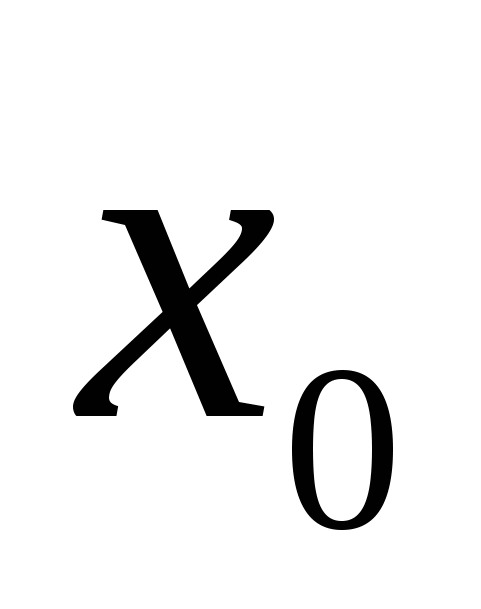 меняет свой знак, то меняет свой знак, то 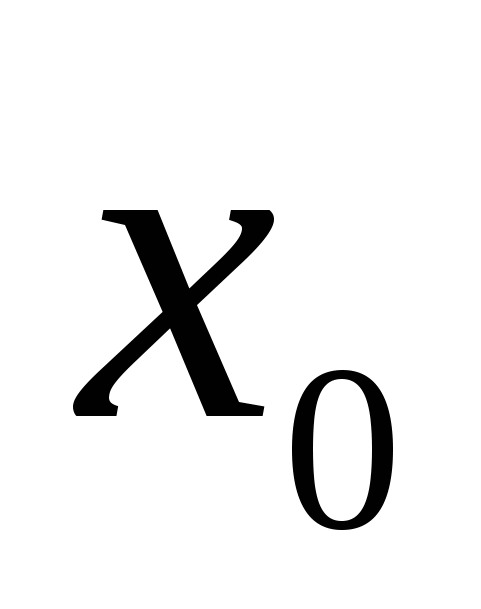 есть точка перегиба ее графика. есть точка перегиба ее графика.
Алгоритм нахождения выпуклостей функции и точек перегиба:
Находим вторую производную 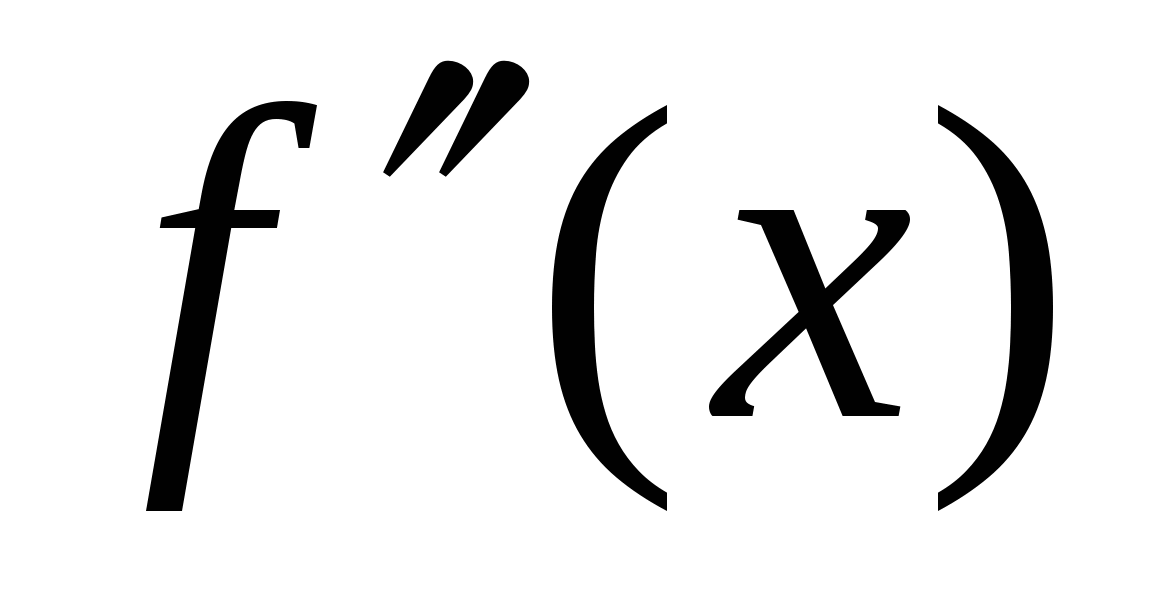 . .
Находим точки, в которых 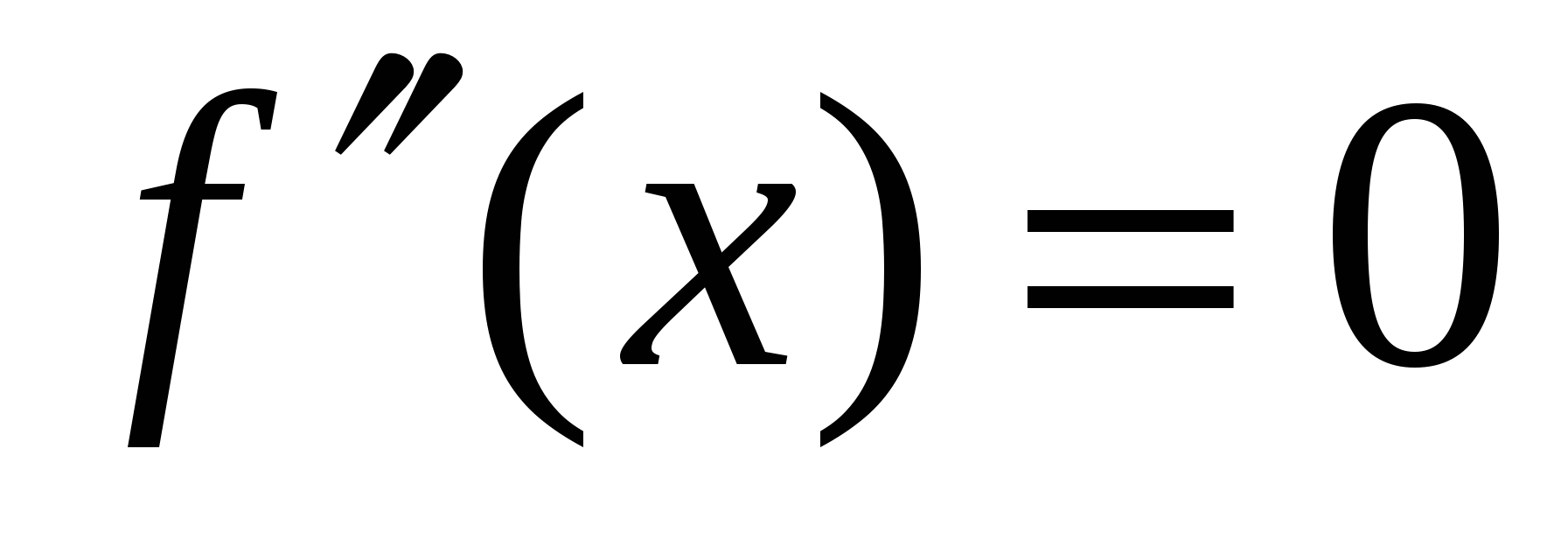 или не существует. или не существует.
Исследуем знак 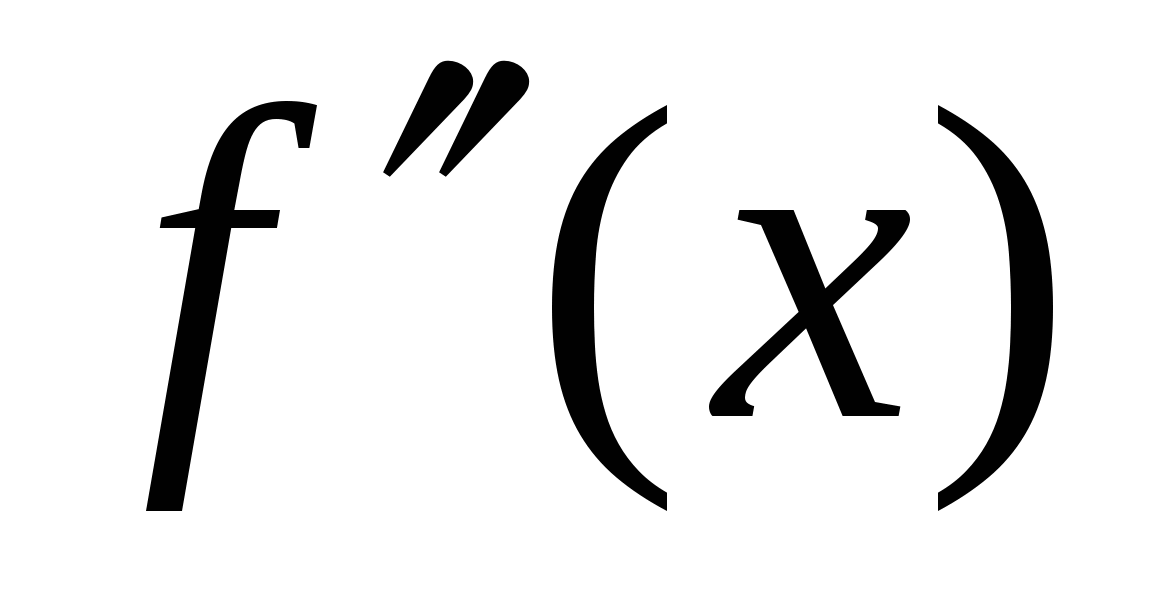 слева и справа от найденных точек и делаем вывод об интервалах выпуклости и о наличии точек перегиба. слева и справа от найденных точек и делаем вывод об интервалах выпуклости и о наличии точек перегиба.
Находим значение функции в точках перегиба.
Пример. Найти точки перегиба графика функции 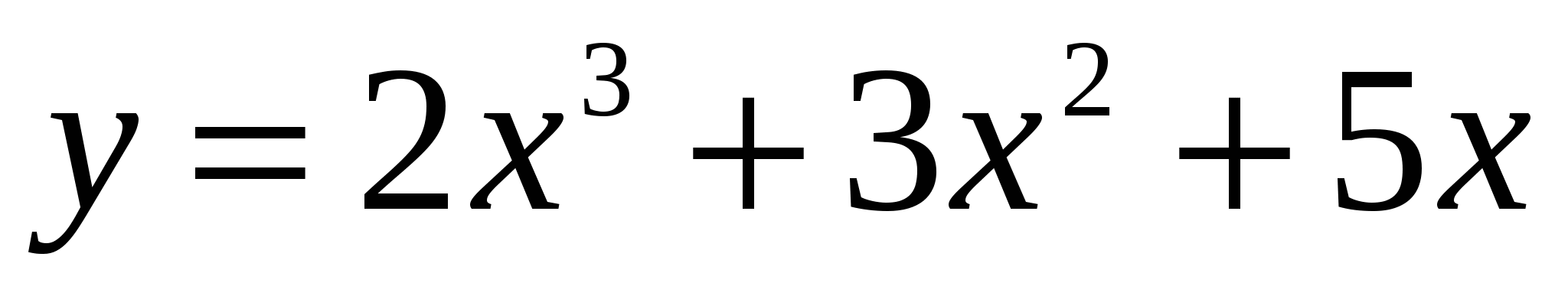 . .
Асимптоты графика функции.
Асимптотой графика функции 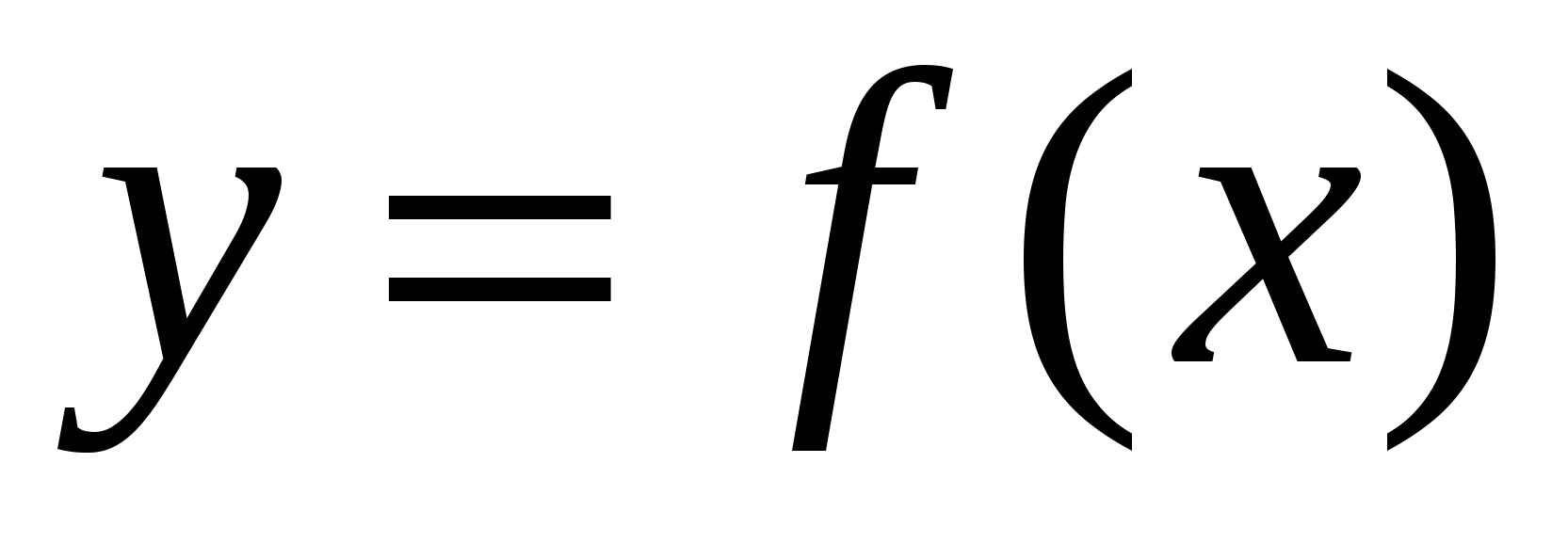 называется прямая, обладающая тем свойством, что расстояние от точки называется прямая, обладающая тем свойством, что расстояние от точки 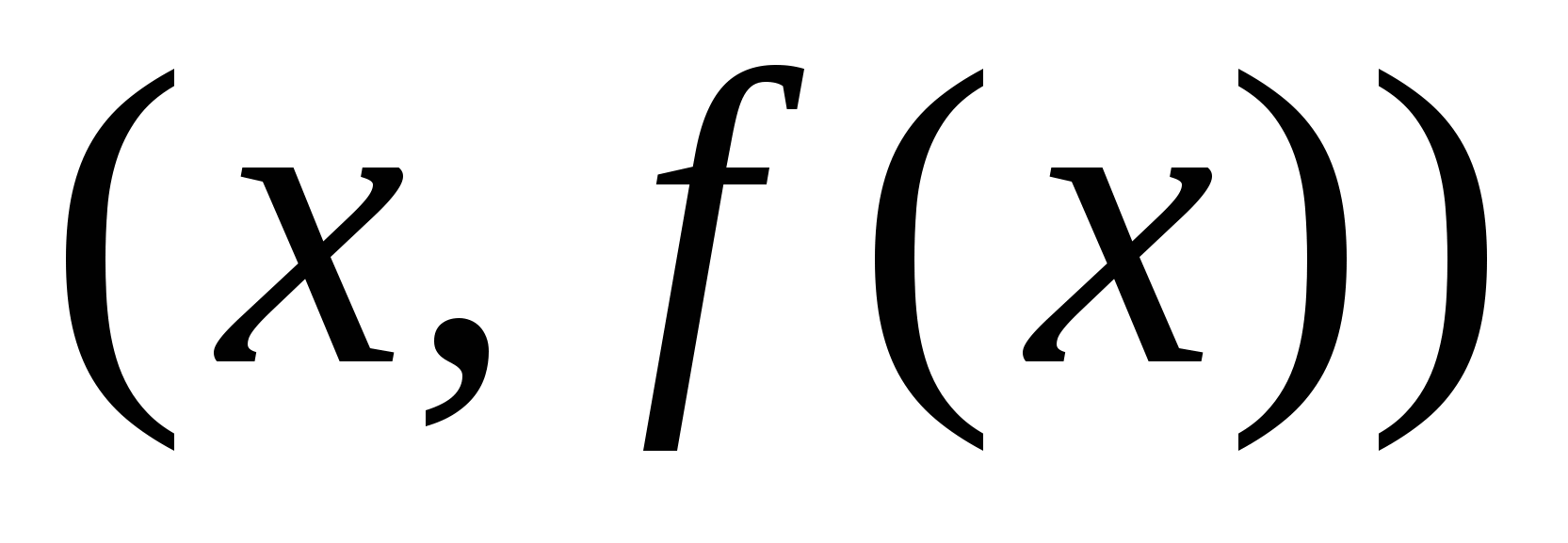 до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
Различают вертикальные (рис. 4а), горизонтальные (рис. 4б) и наклонные (рис. 4в) асимптоты.
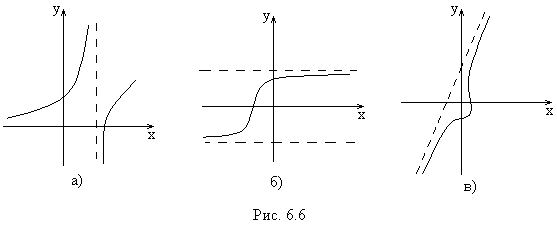
Рис. 4.
Теорема. В точках вертикальных асимптот (например, 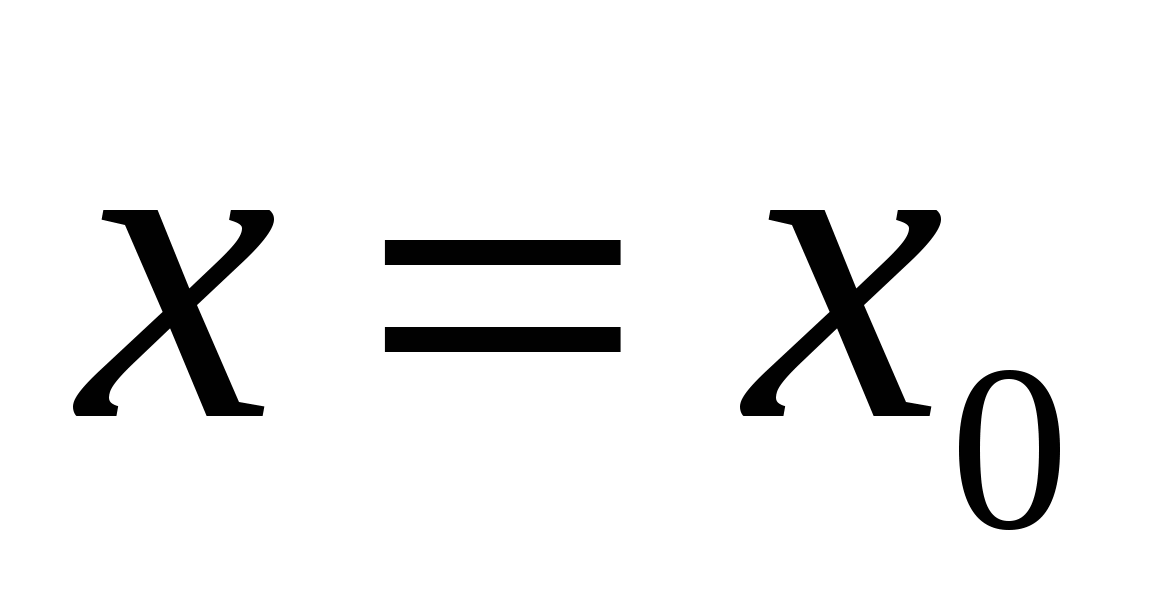 ) функция ) функция 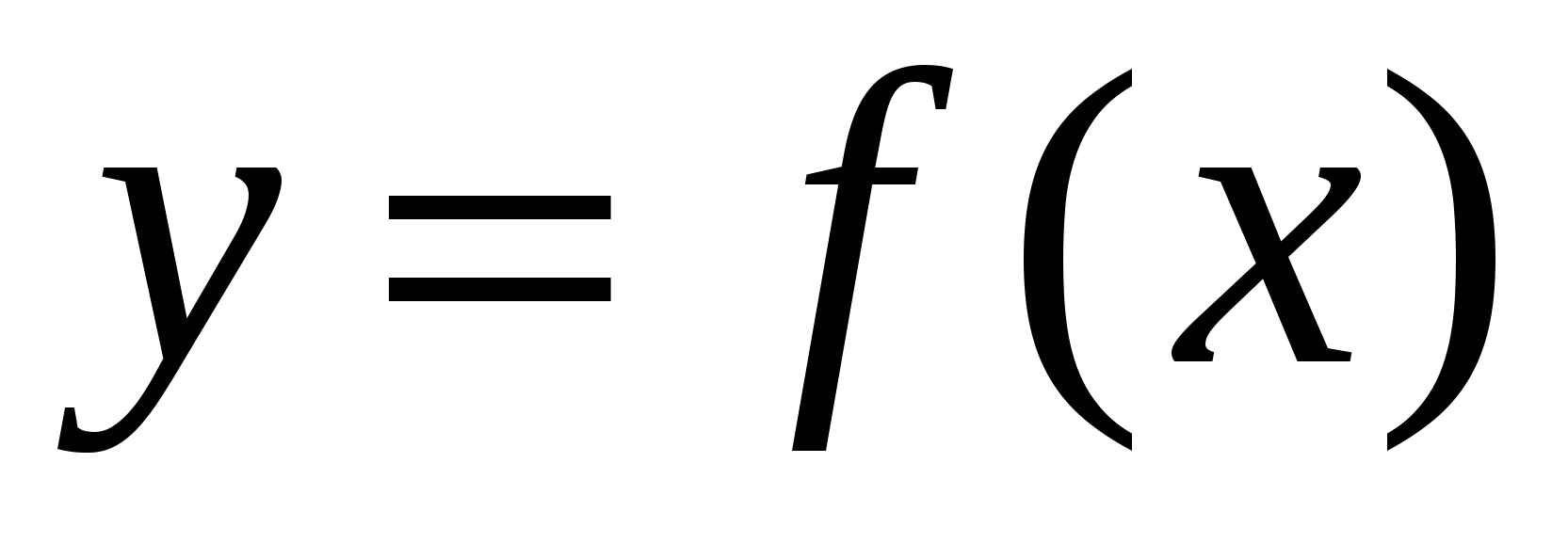 терпит разрыв, ее предел слева и справа от точки терпит разрыв, ее предел слева и справа от точки 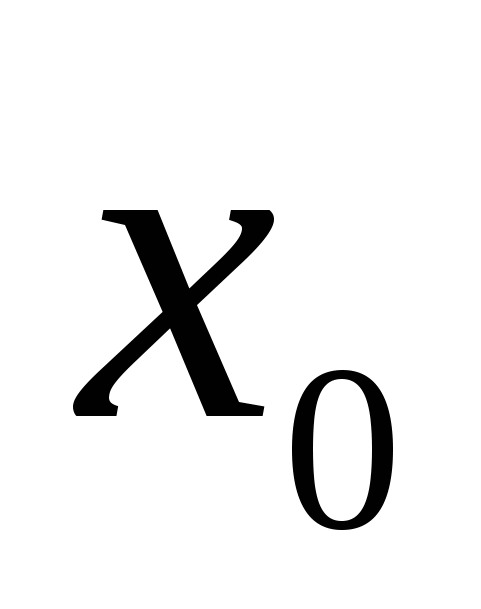 равен равен 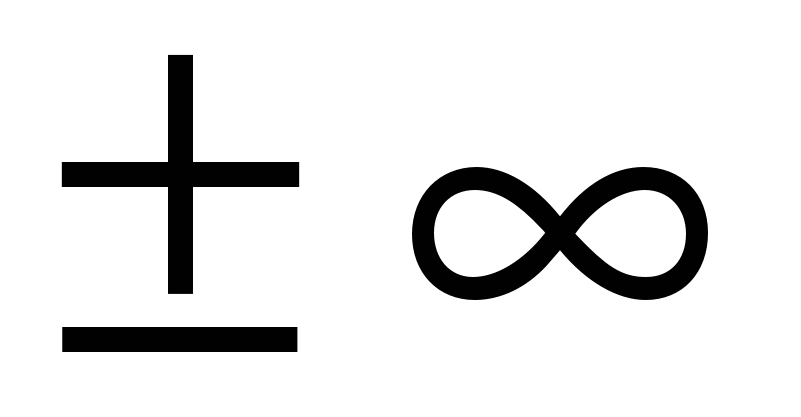 : : 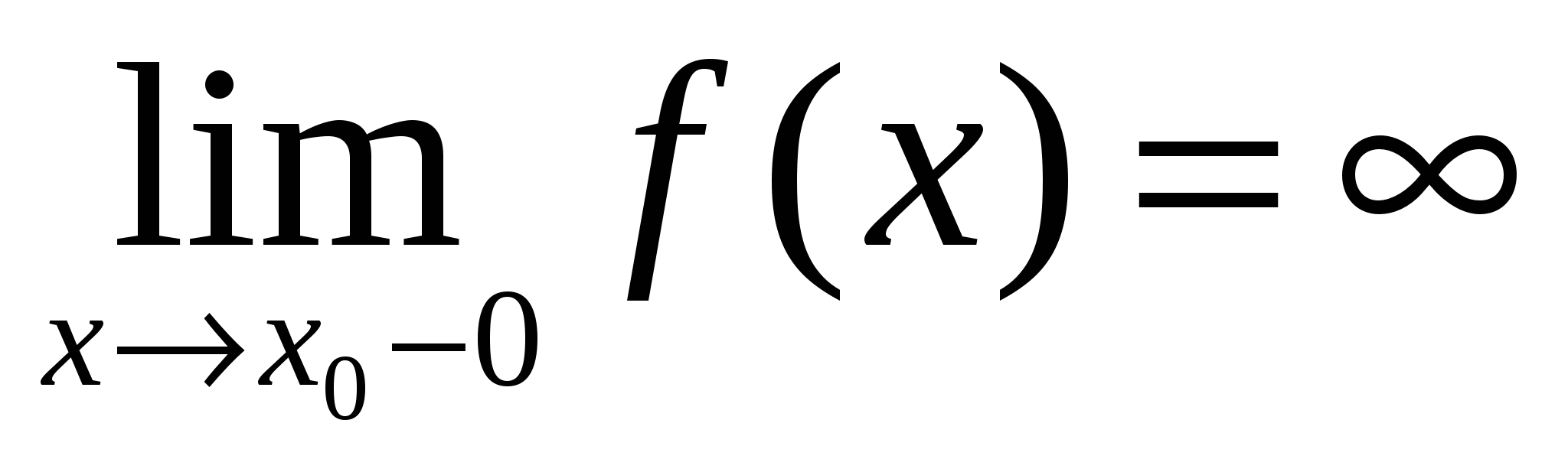 и (или) и (или) 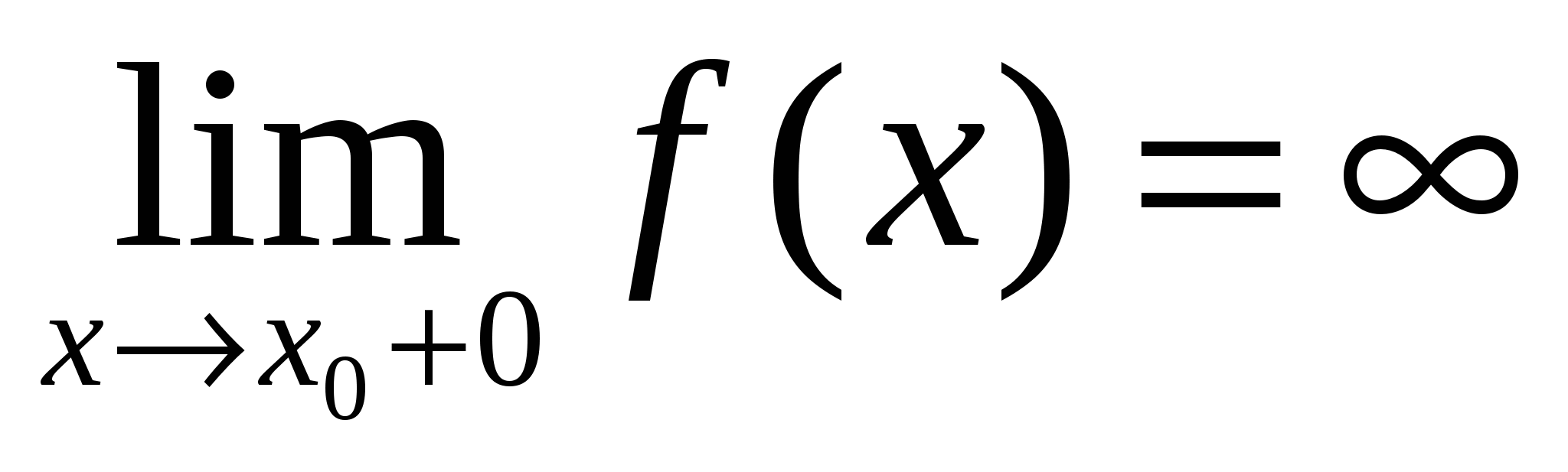 . .
Теорема. Пусть функция 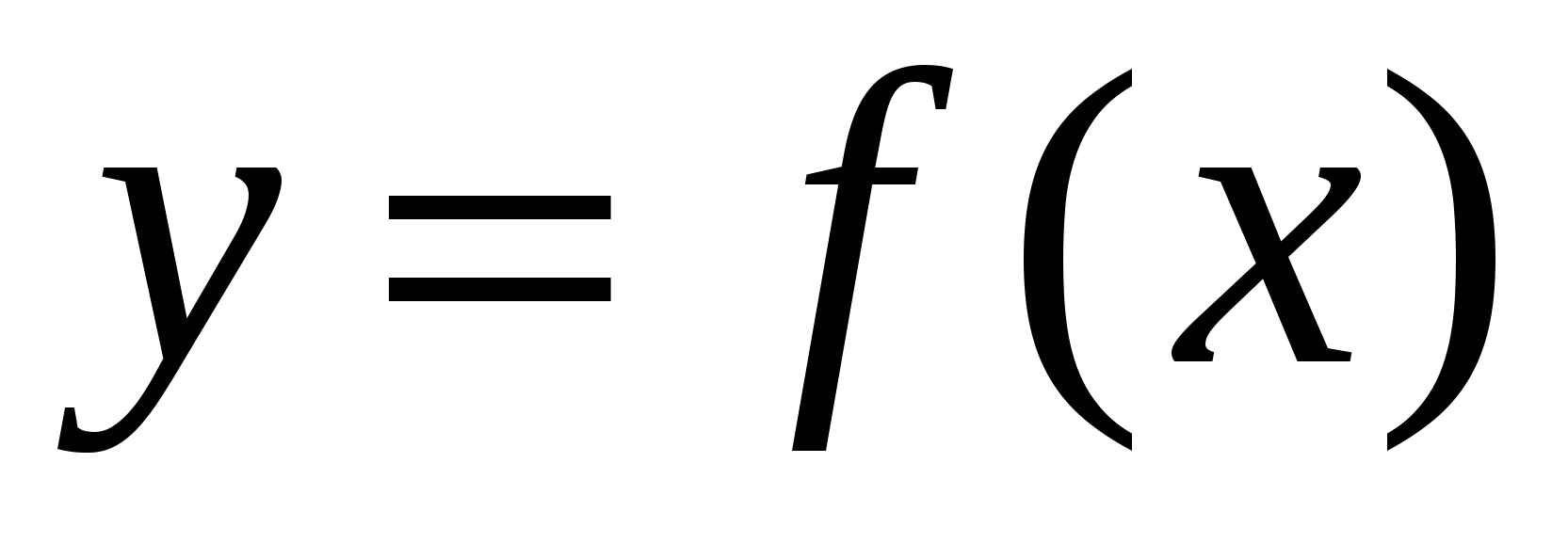 определена при достаточно больших определена при достаточно больших 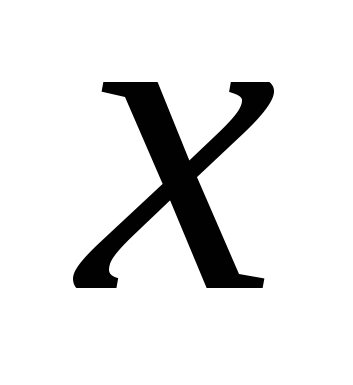 и существуют конечные пределы и существуют конечные пределы 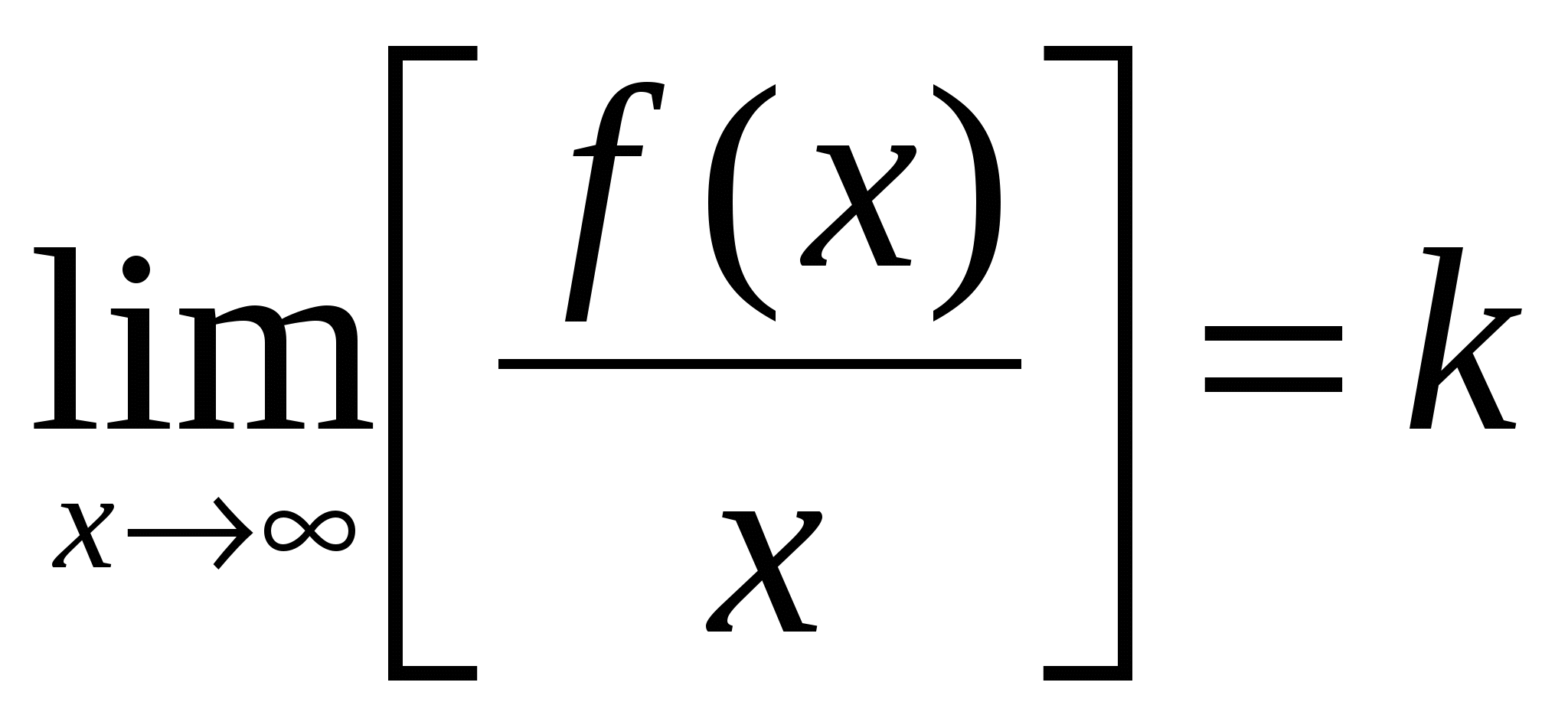 и и 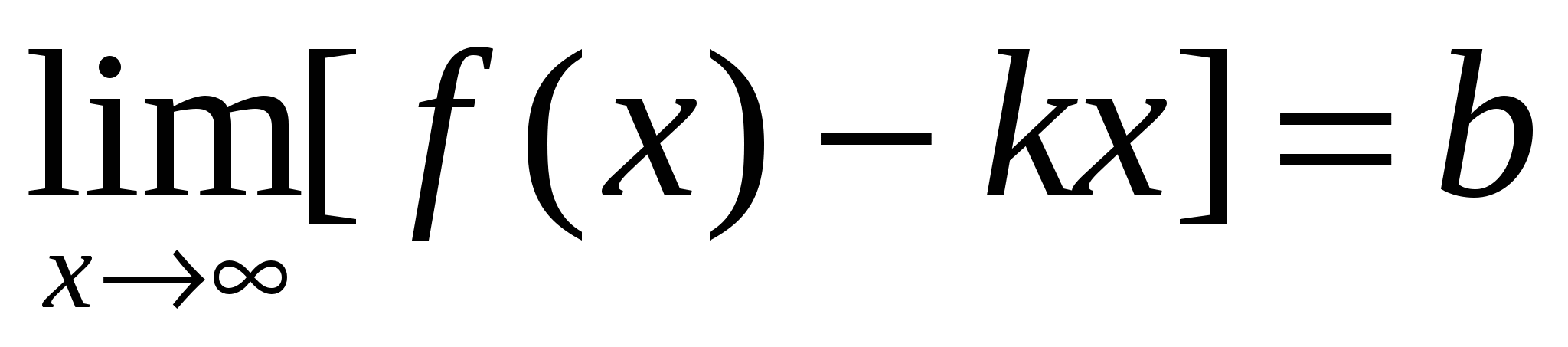 . Тогда прямая . Тогда прямая 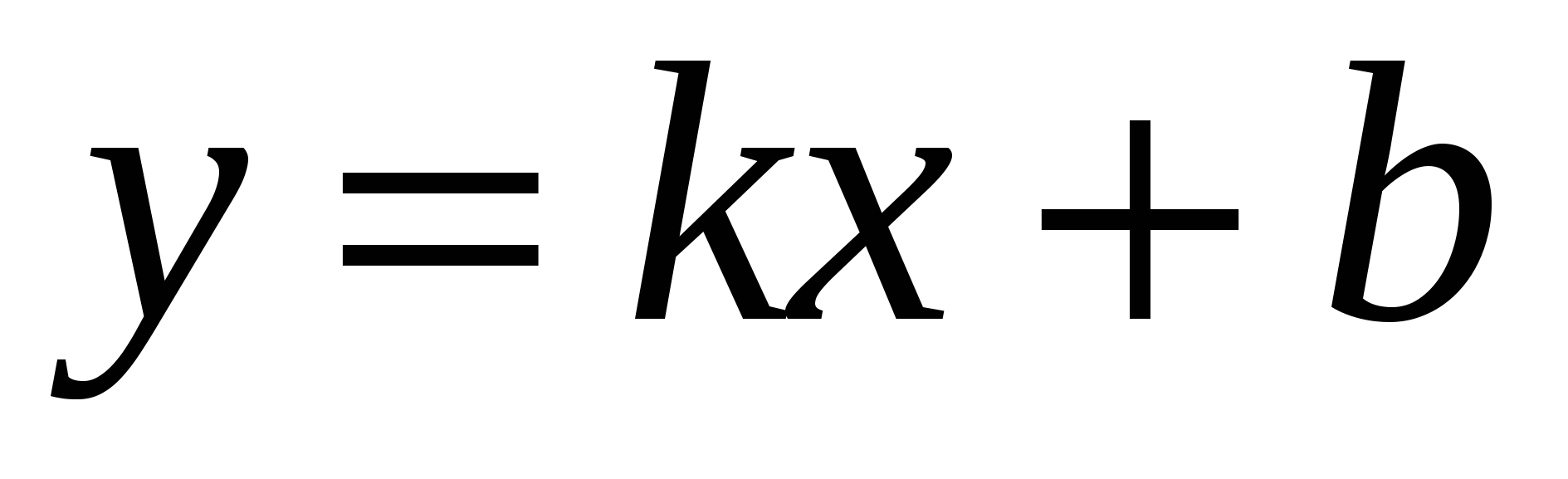 является наклонной асимптотой графика функции является наклонной асимптотой графика функции 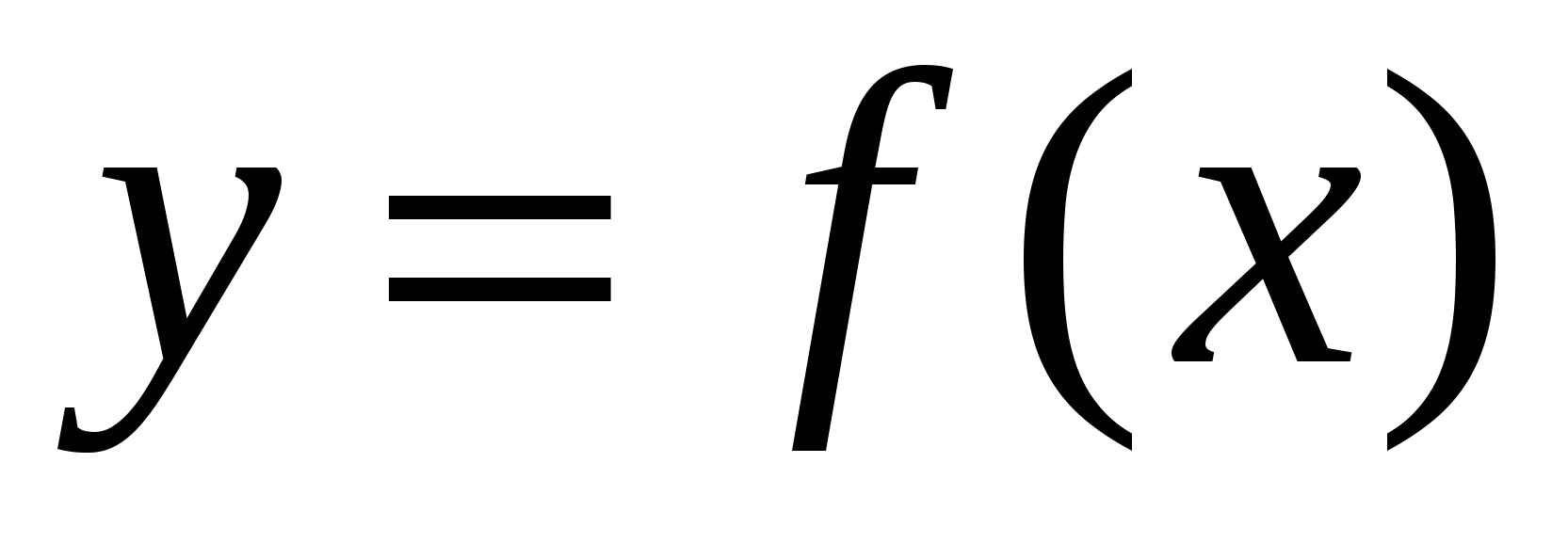 . .
Теорема. Пусть функция 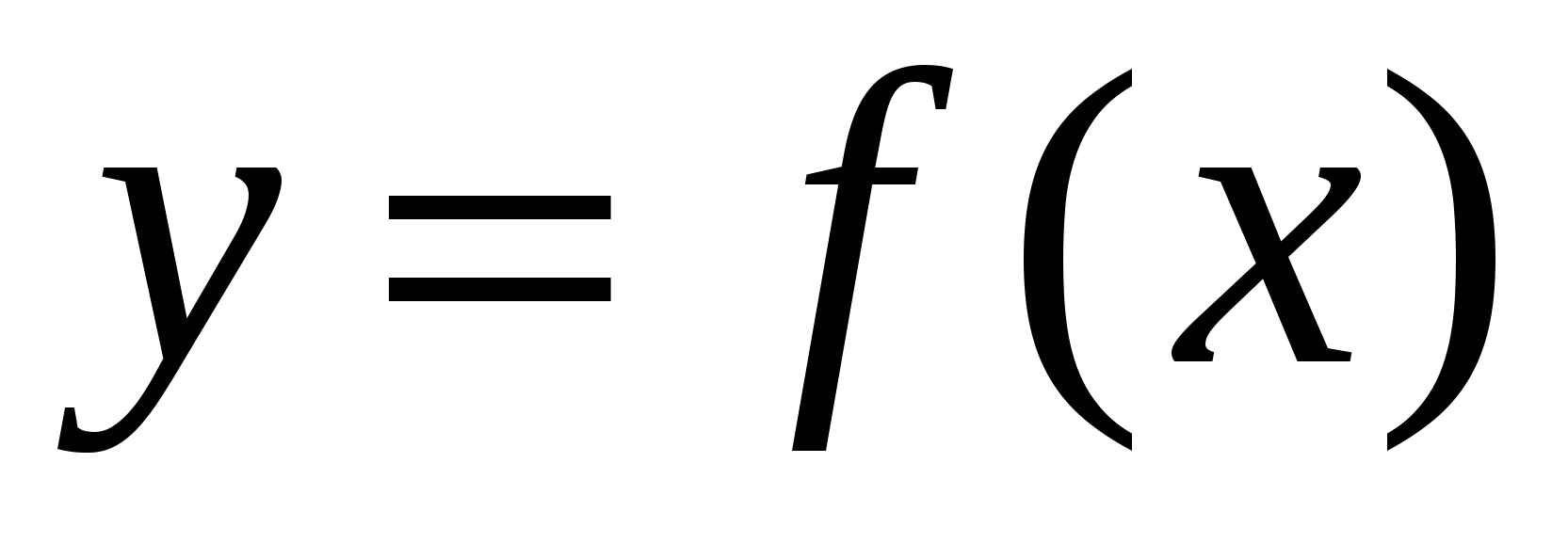 определена при достаточно больших определена при достаточно больших 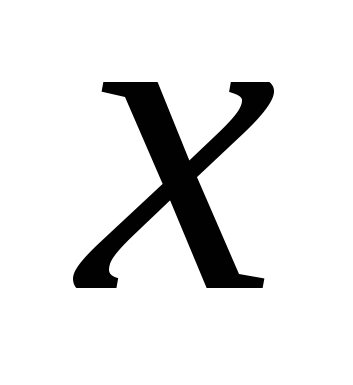 и существует предел функции и существует предел функции 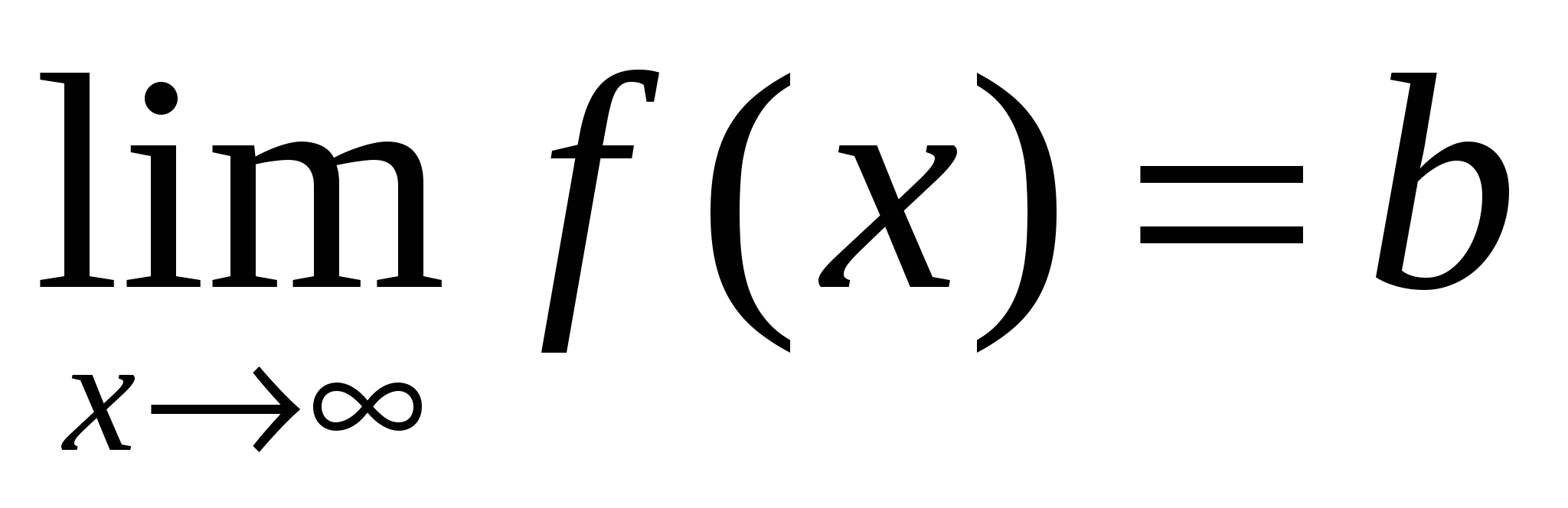 . Тогда прямая . Тогда прямая 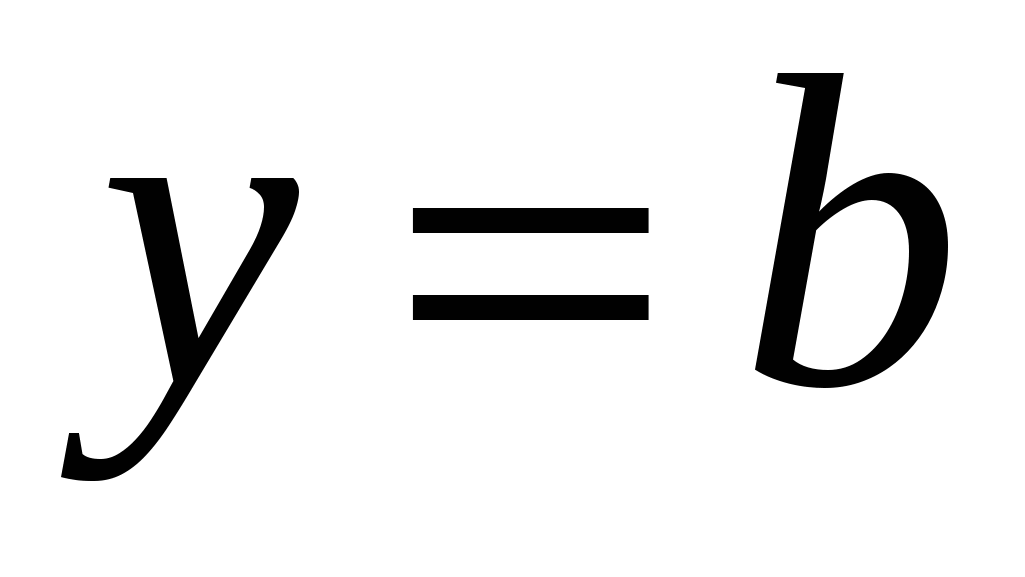 есть горизонтальная асимптота графика функции есть горизонтальная асимптота графика функции 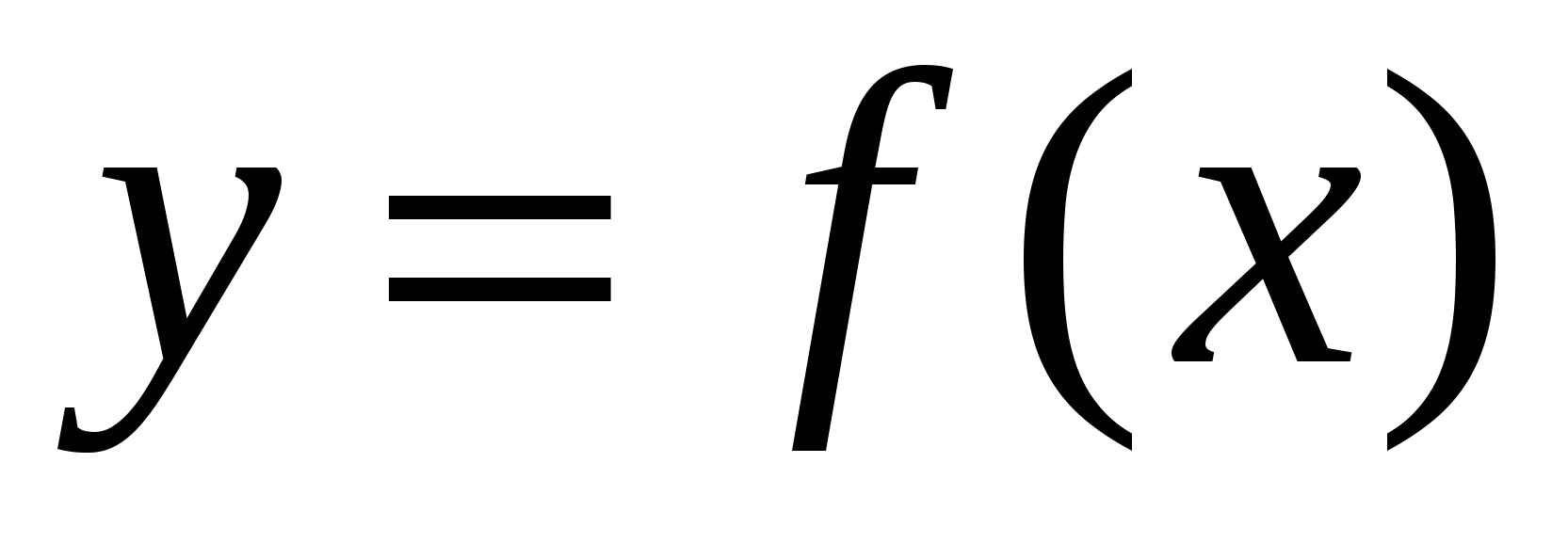 . .
Горизонтальная асимптота является частным случаем наклонной асимптоты, когда 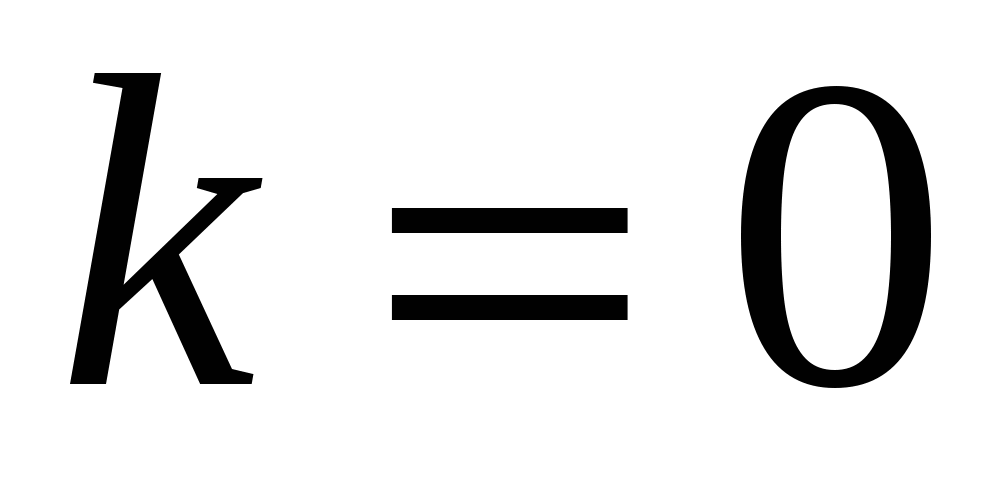 . Поэтому, если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот. . Поэтому, если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.
Пример. Найти асимптоты графика функции 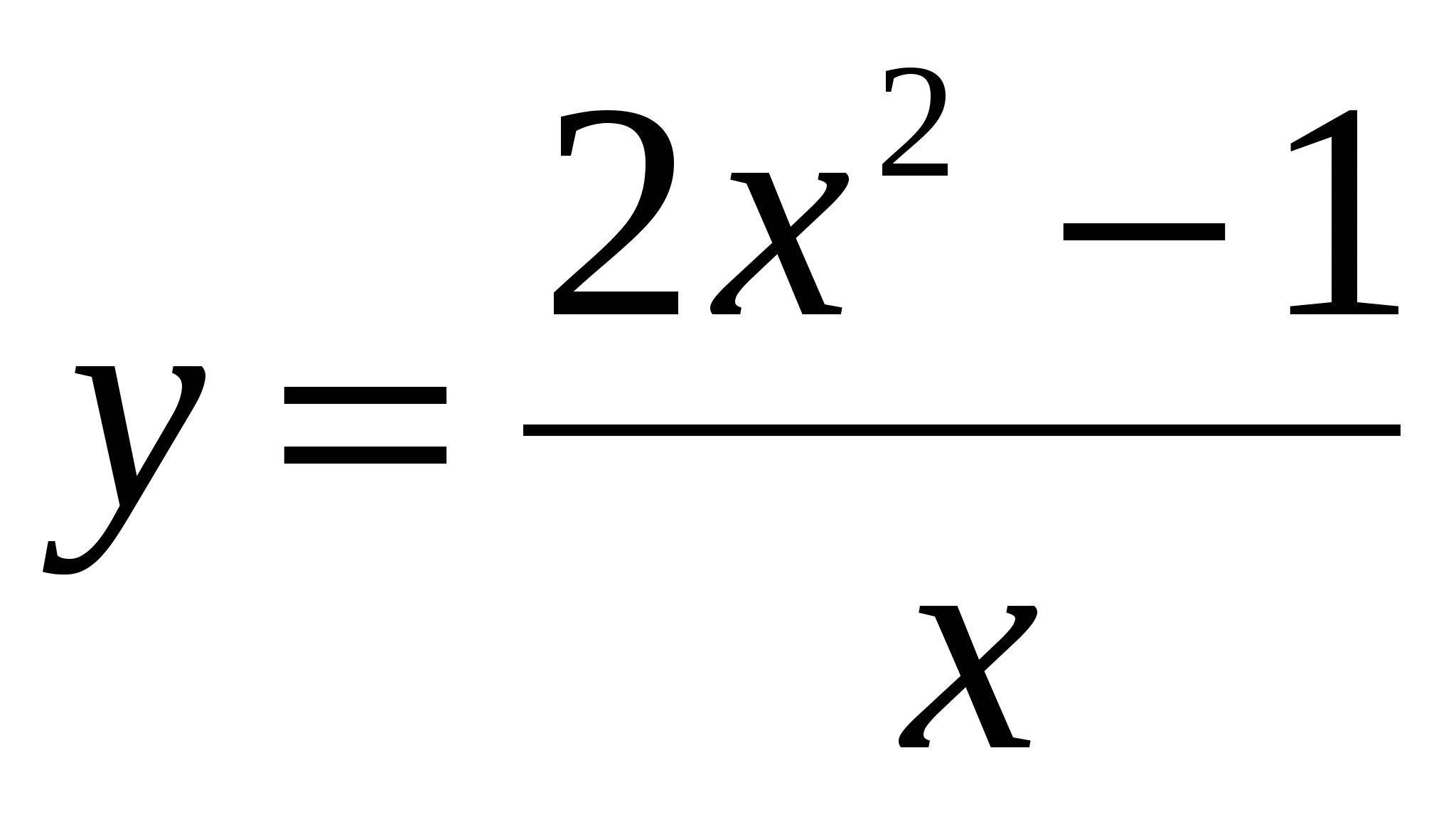 . .
Общая схема исследования функции и построения ее графика.
Найти область определения  . .
Если у  есть знаменатель, он не должен обращаться в 0. есть знаменатель, он не должен обращаться в 0.
Подкоренное выражение корня четной степени должно быть неотрицательным (больше либо равно нулю).
Подлогарифмическое выражение должно быть положительным.
Исследовать функцию на четность – нечетность.
Если 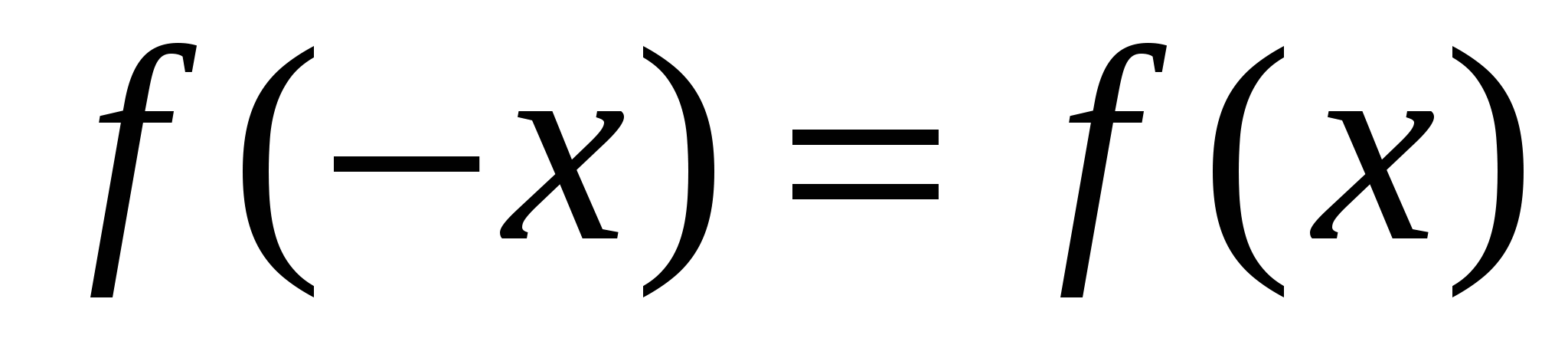 , то функция четная. , то функция четная.
Если 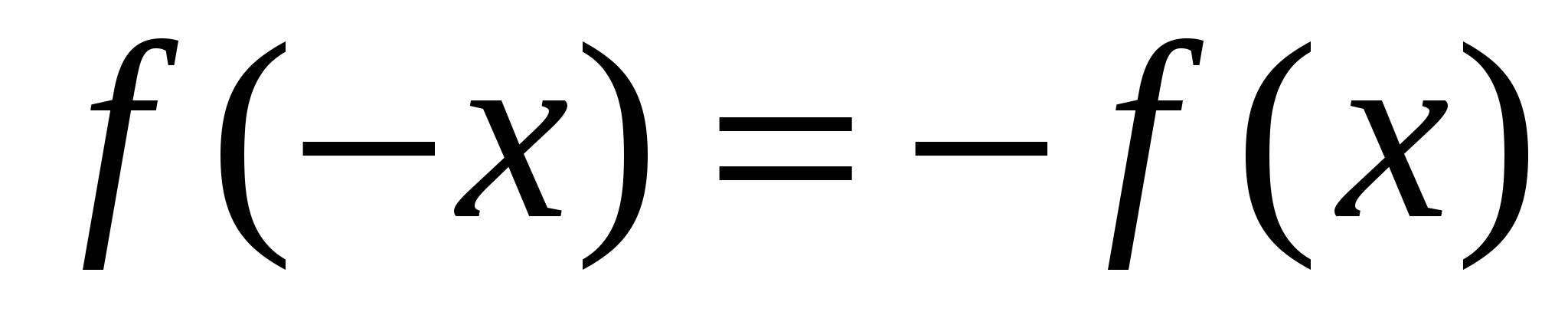 , то функция нечетная. , то функция нечетная.
Если не выполнено ни 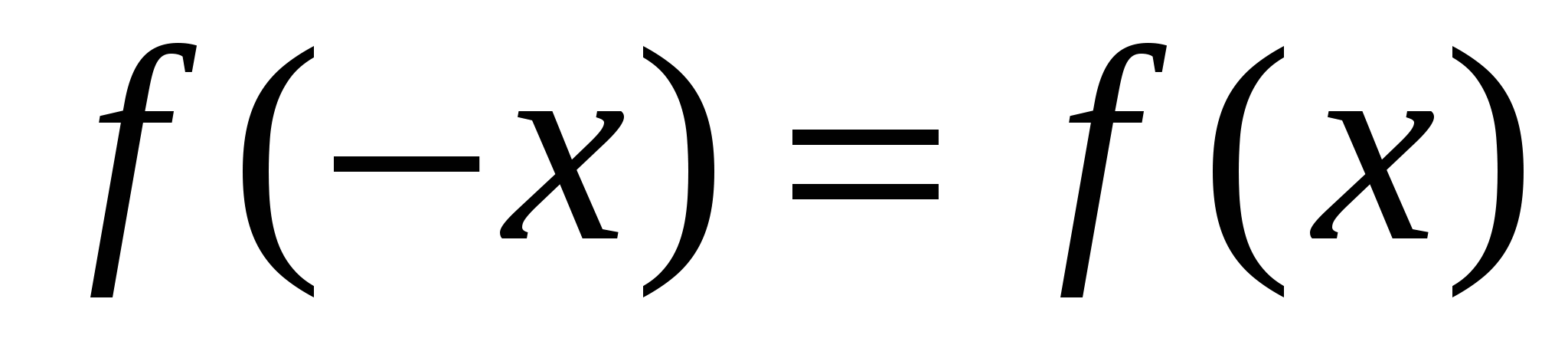 , ни , ни 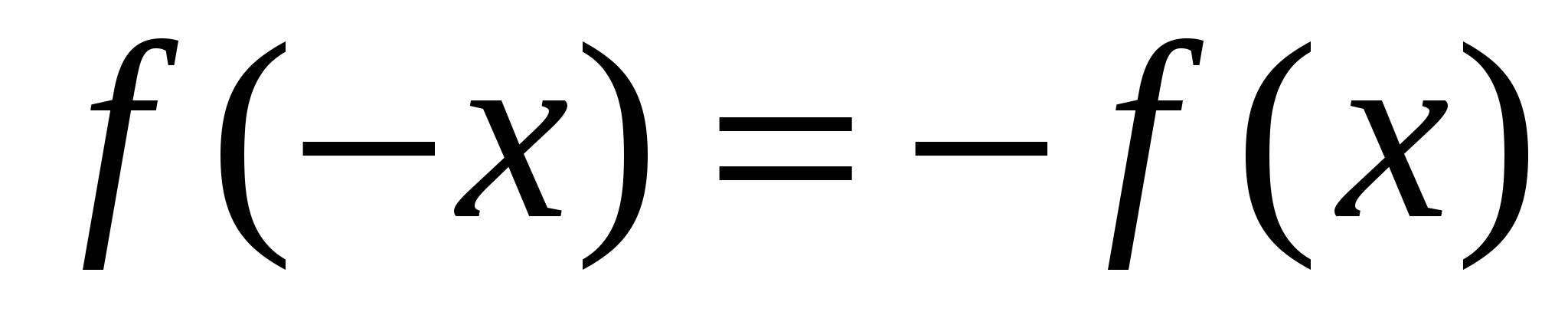 , то , то  – функция общего вида. – функция общего вида.
Найти вертикальные асимптоты и точки разрыва (если есть).
Вертикальная асимптота может возникнуть только на границе области определения функции.
Если 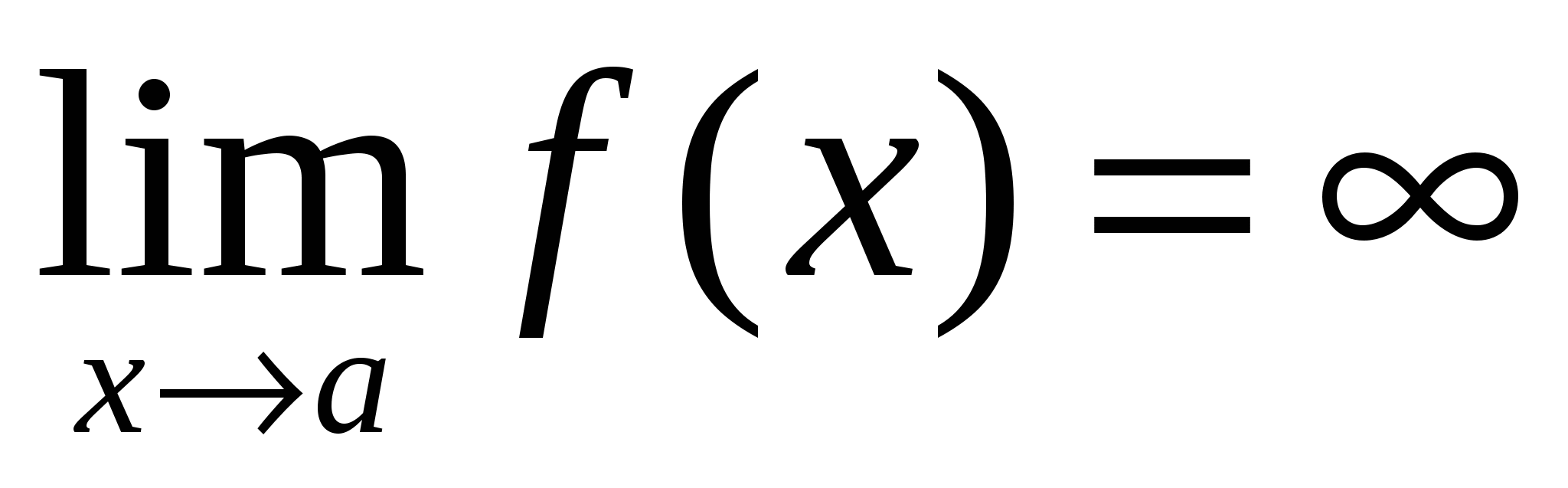 ( (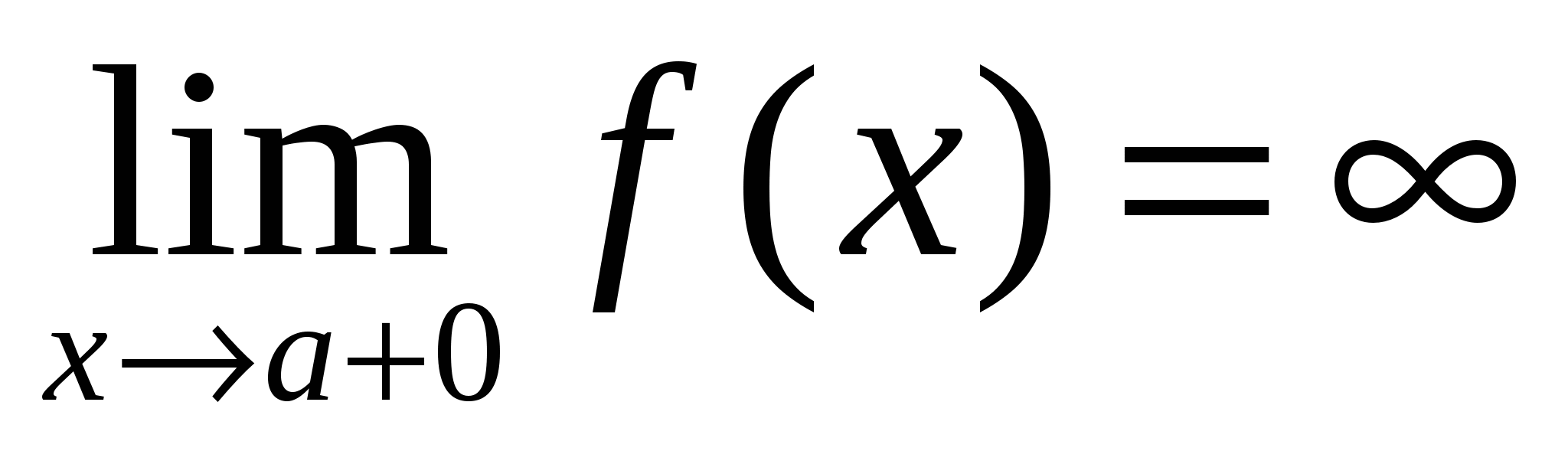 или или 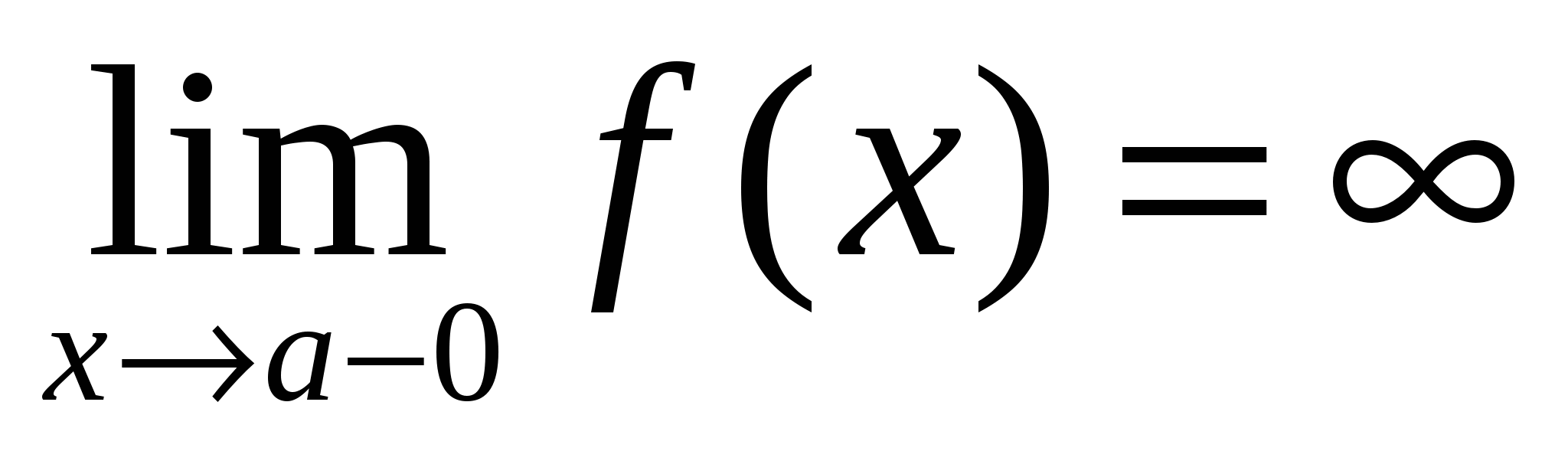 ), то ), то 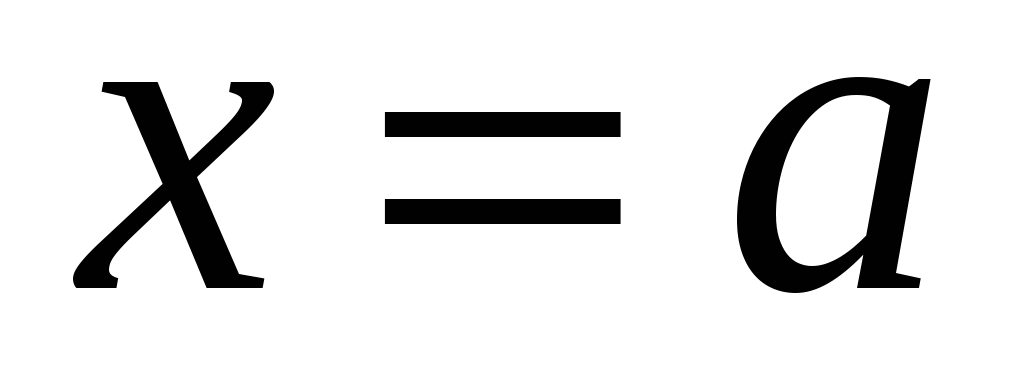 – вертикальная асимптота графика – вертикальная асимптота графика  . .
Исследовать поведение функции в бесконечности; найти горизонтальные и наклонные асимптоты (если есть).
Если 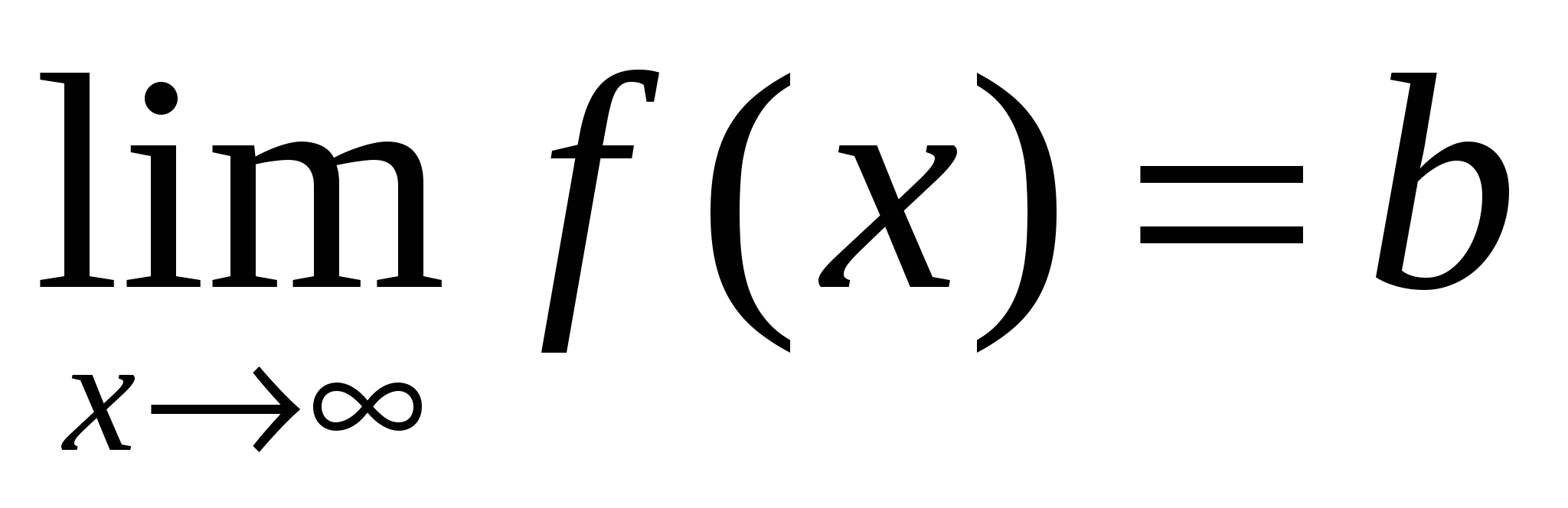 , то , то 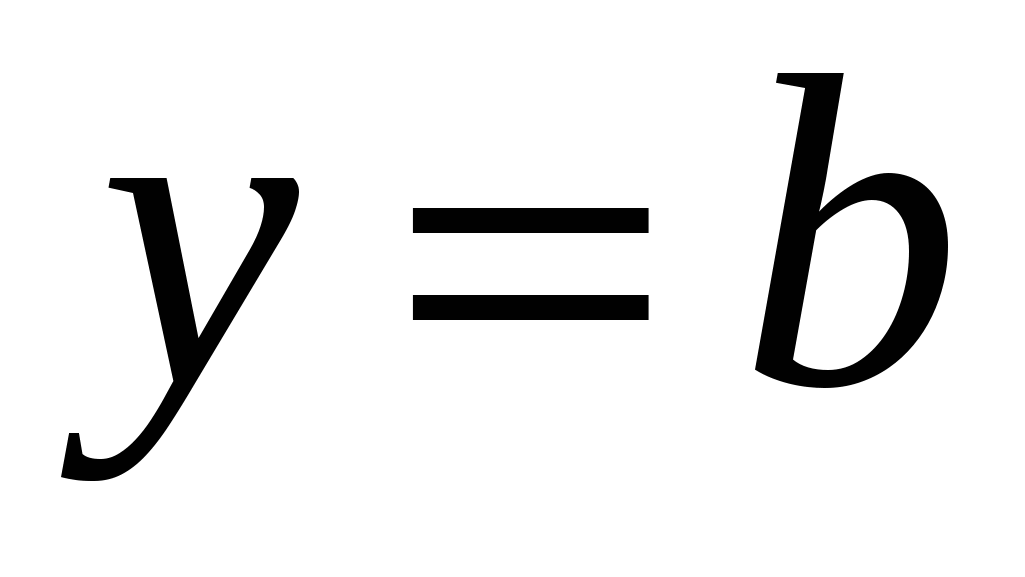 – горизонтальная асимптота графика – горизонтальная асимптота графика  . .
Если 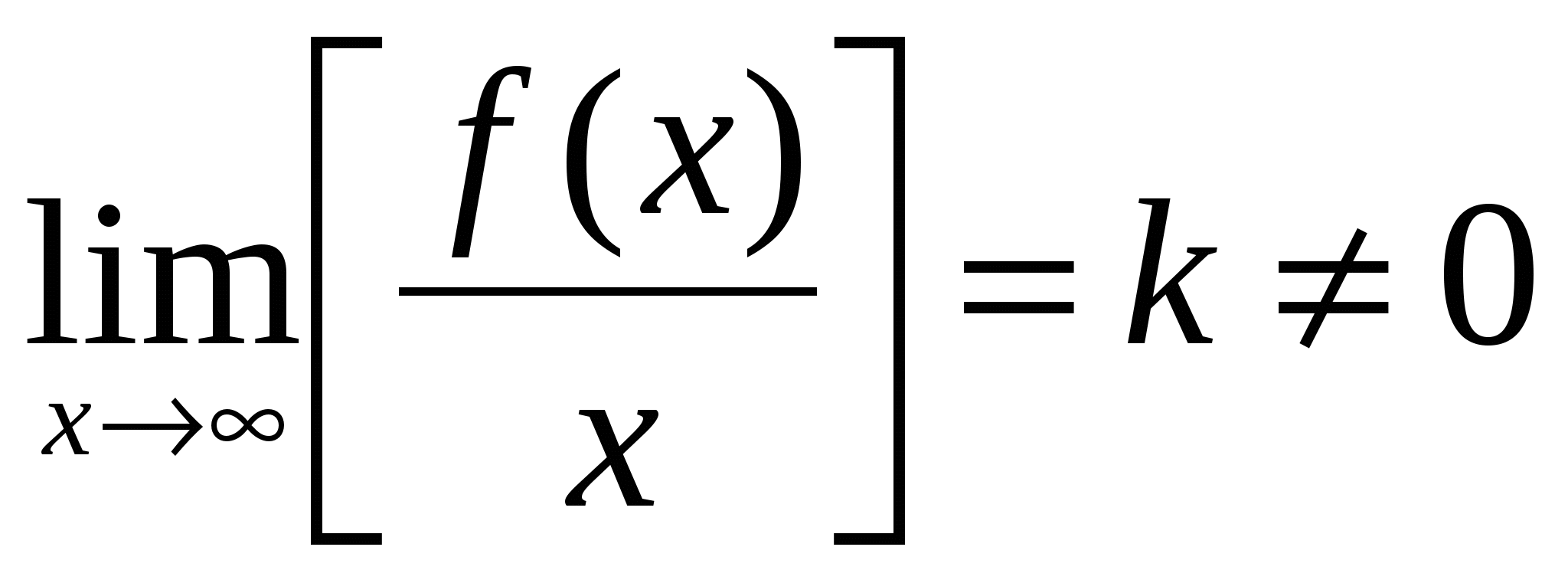 и и 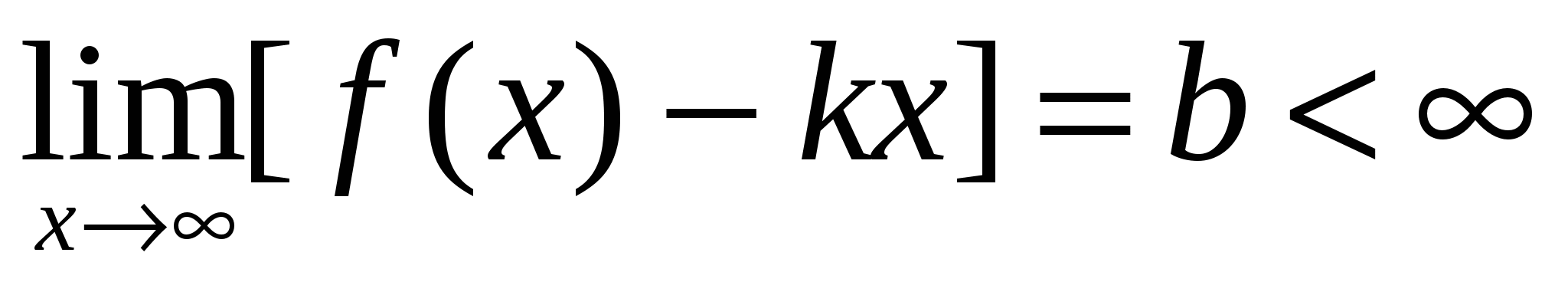 , то прямая , то прямая 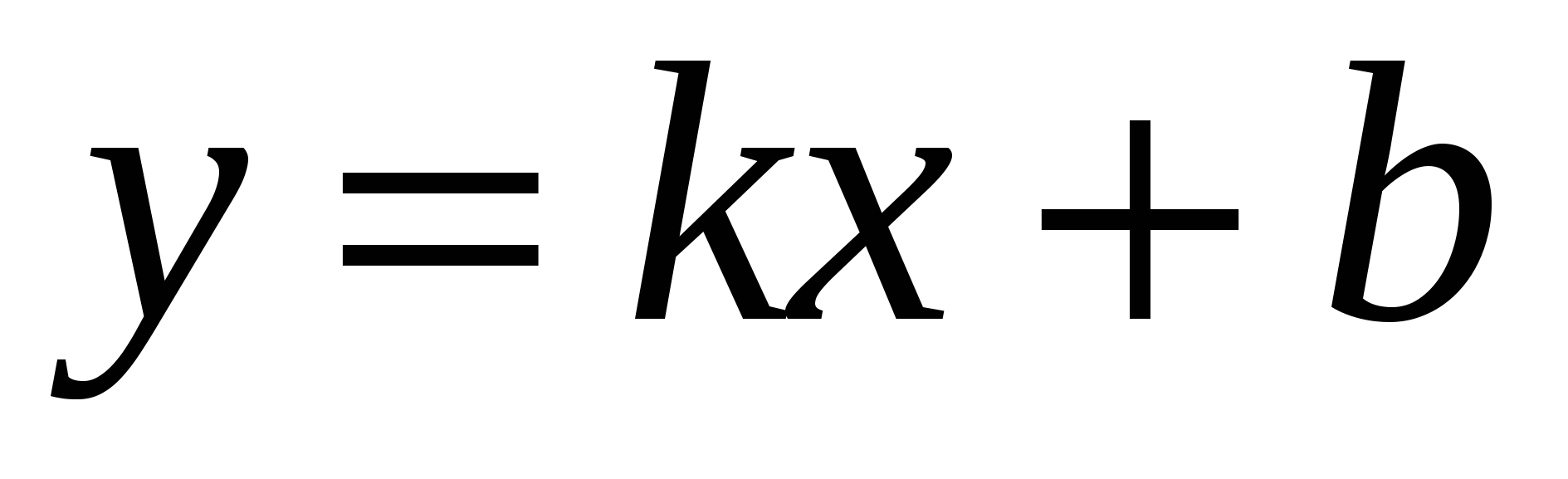 является наклонной асимптотой графика является наклонной асимптотой графика  . .
Если пределы, указанные в п. a, b, существуют только при одностороннем стремлении 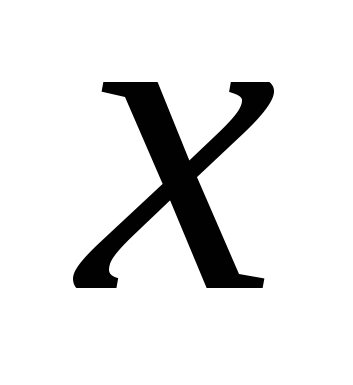 к бесконечности ( к бесконечности (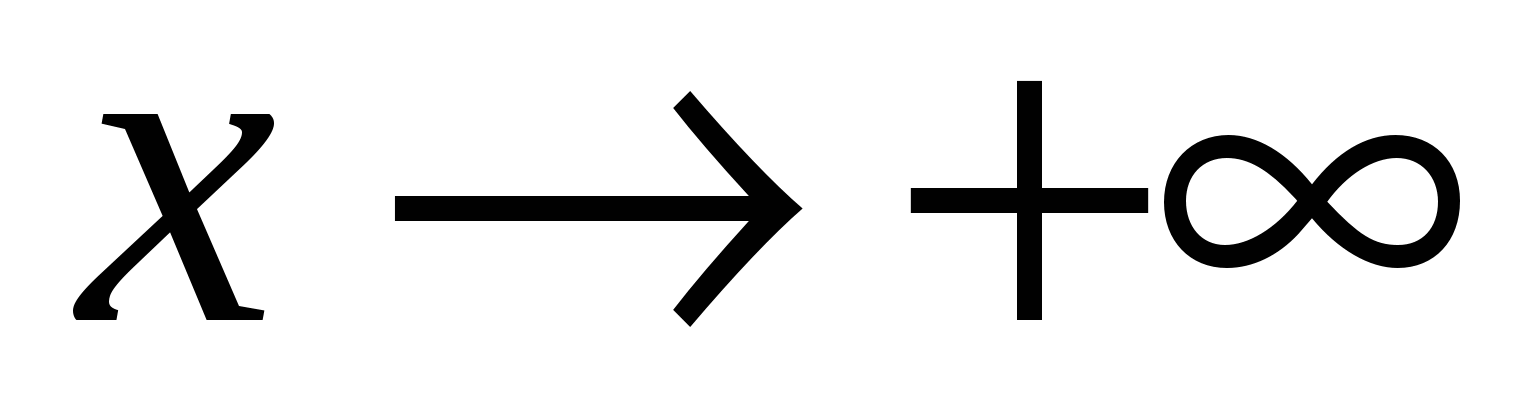 или или 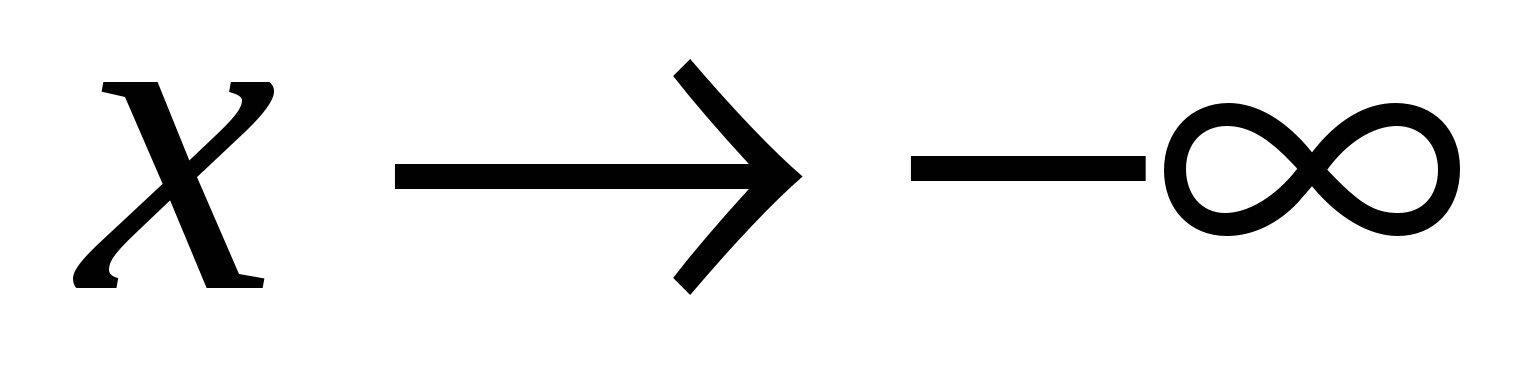 ), то полученные асимптоты будут односторонними: левосторонними при ), то полученные асимптоты будут односторонними: левосторонними при 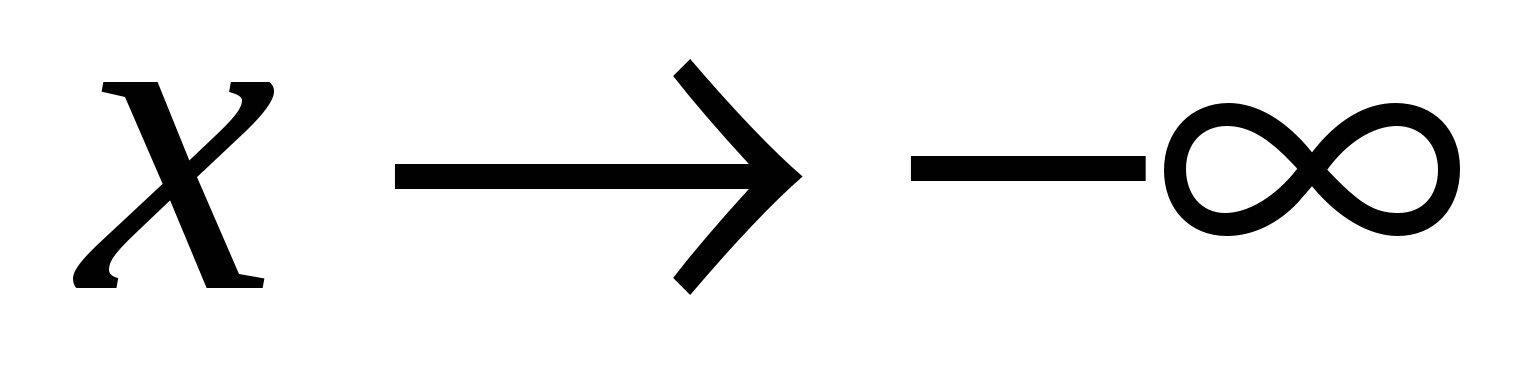 и правосторонними при и правосторонними при 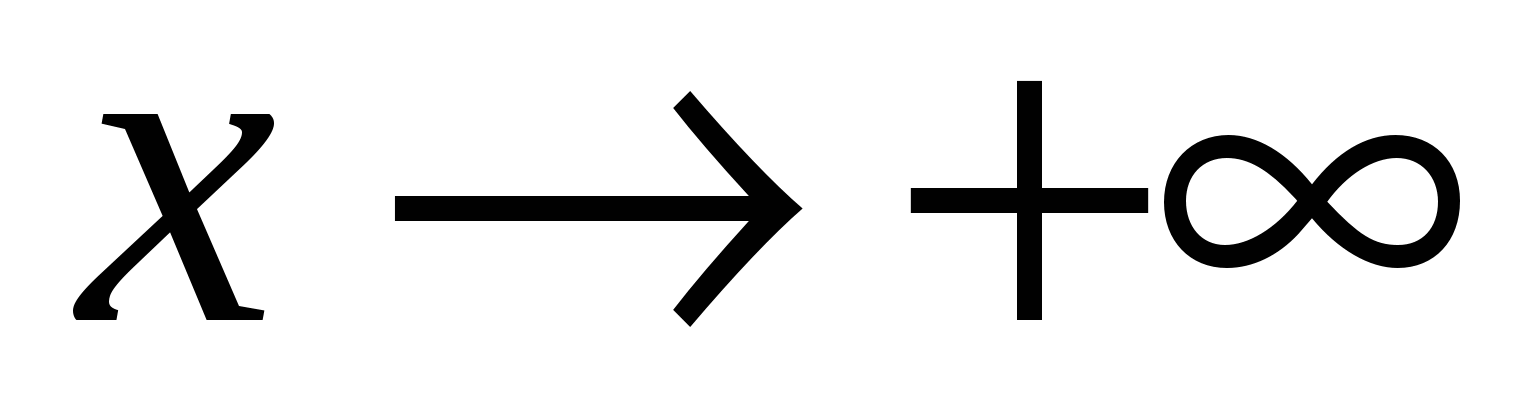 . .
Найти экстремумы и интервалы монотонности функции.
Найти производную 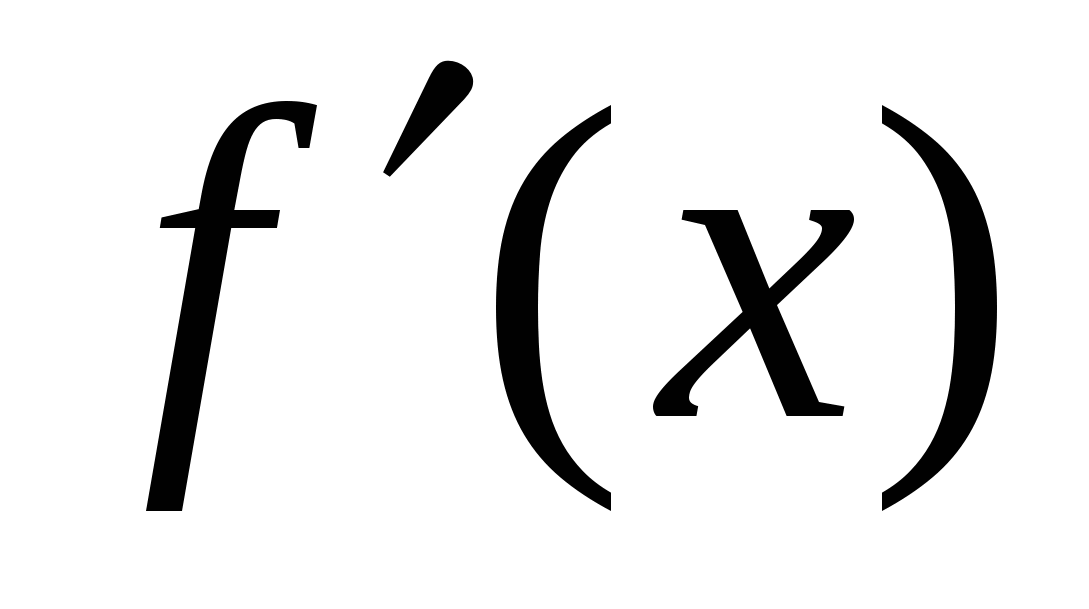 . .
Найти критические точки  (те точки, где (те точки, где 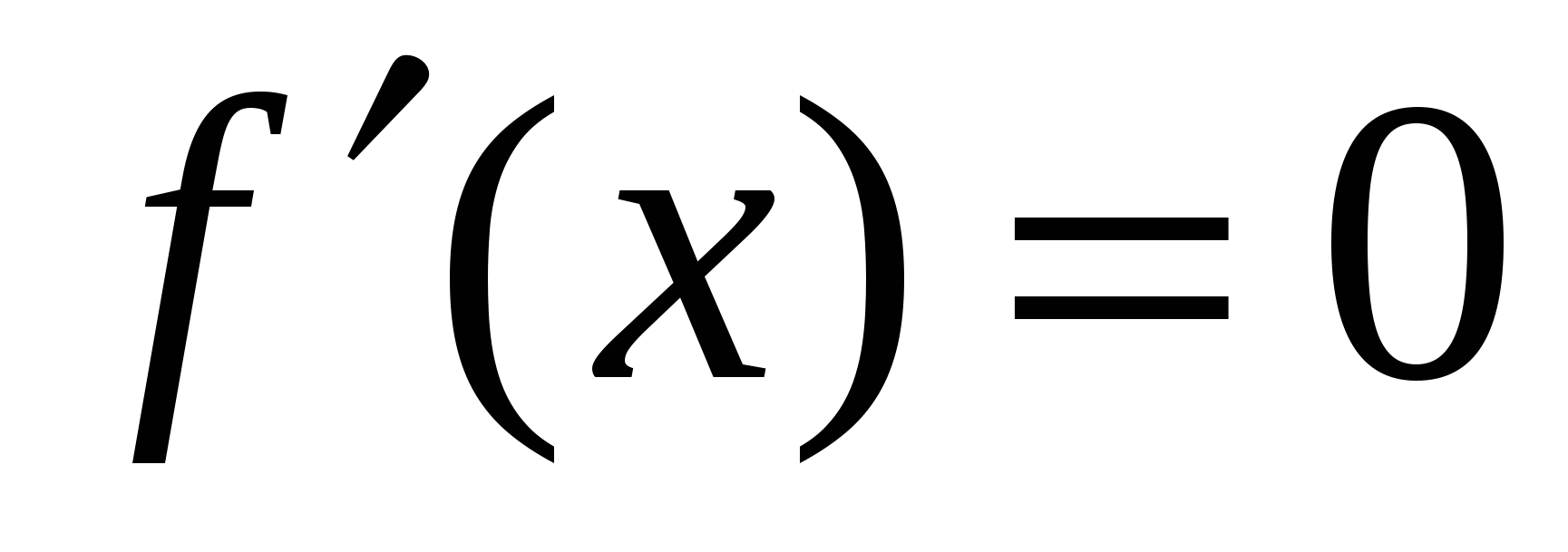 или, где или, где 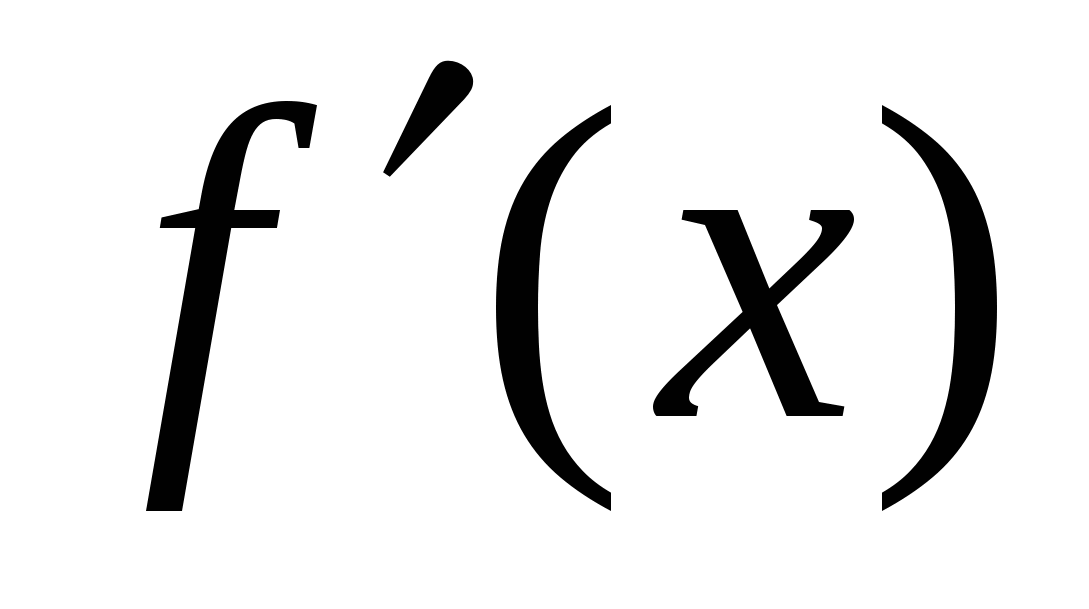 не существует). не существует).
На числовой оси отметить область определения  и ее критические точки. и ее критические точки.
На каждом из полученных числовых интервалов определить знак производной 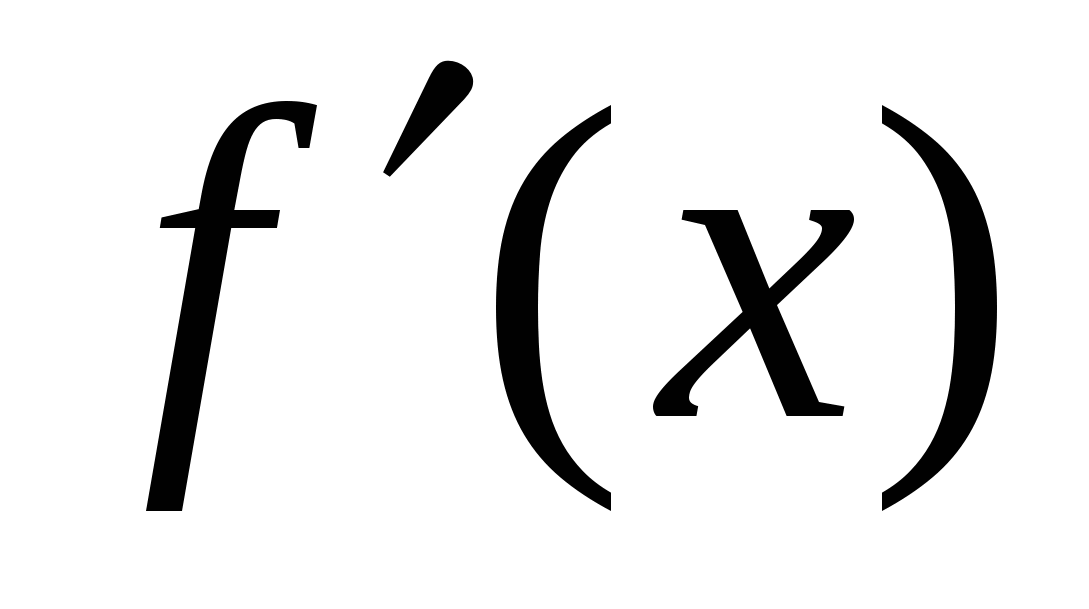 . .
По знакам производной сделать вывод о наличии экстремумов у  и их типе. и их типе.
Найти экстремальные значения  . .
По знакам производной сделать вывод о возрастании и убывании  . .
Найти интервалы выпуклости и точки перегиба.
Находим вторую производную 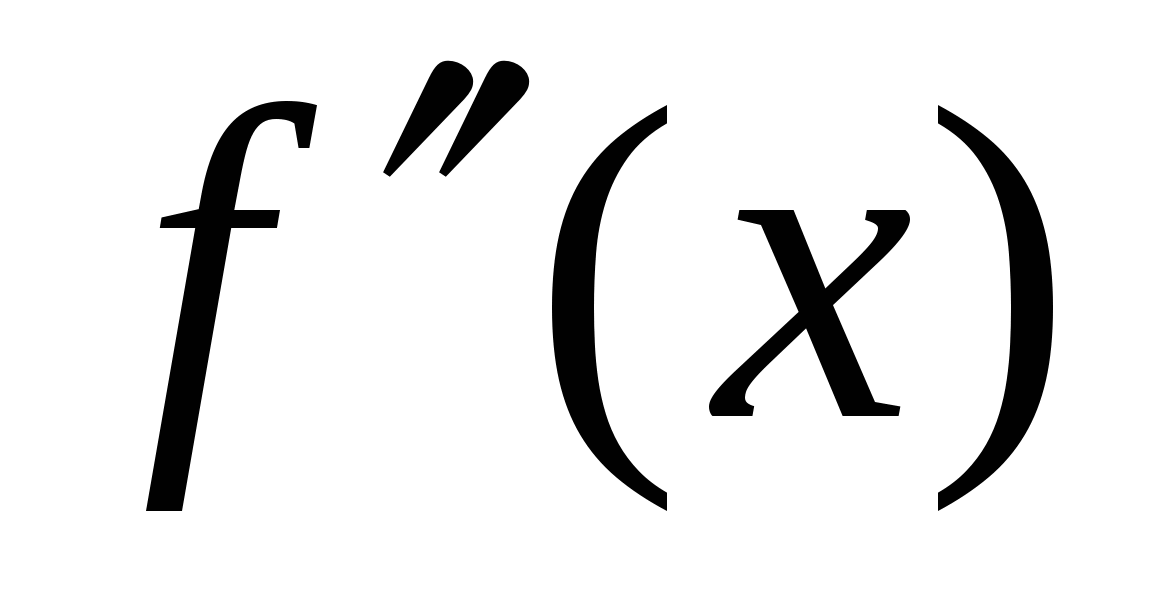 . .
Находим точки, в которых 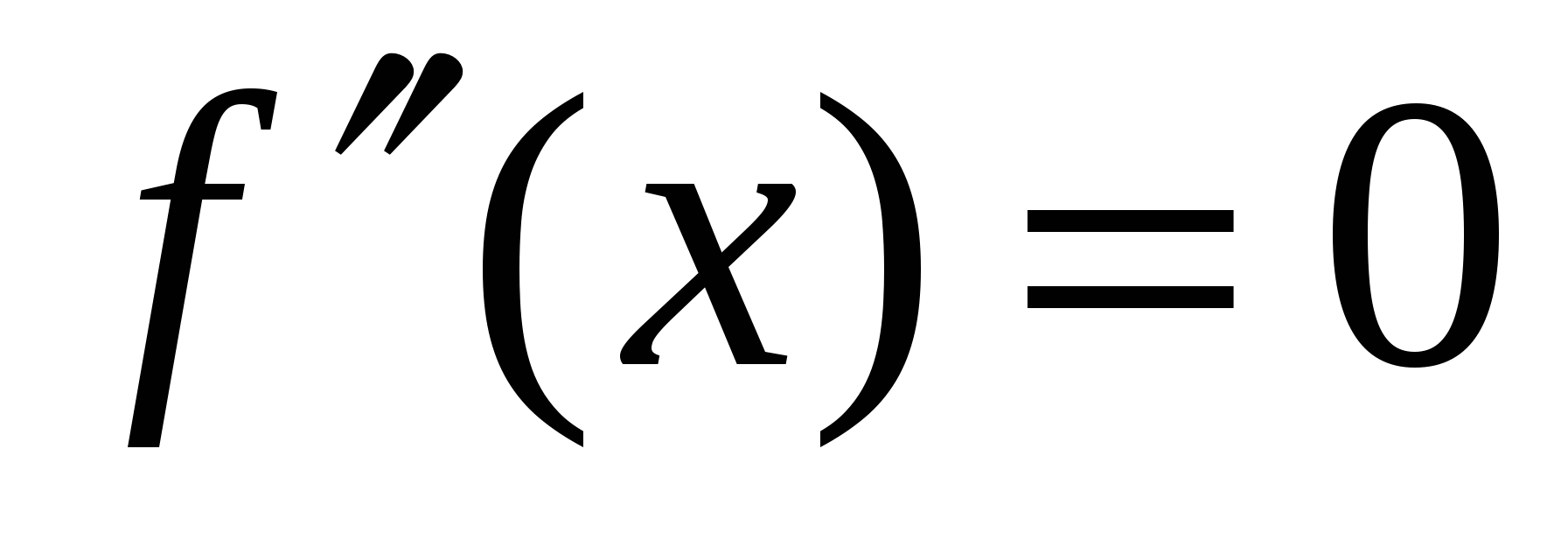 или не существует. или не существует.
Исследуем знак 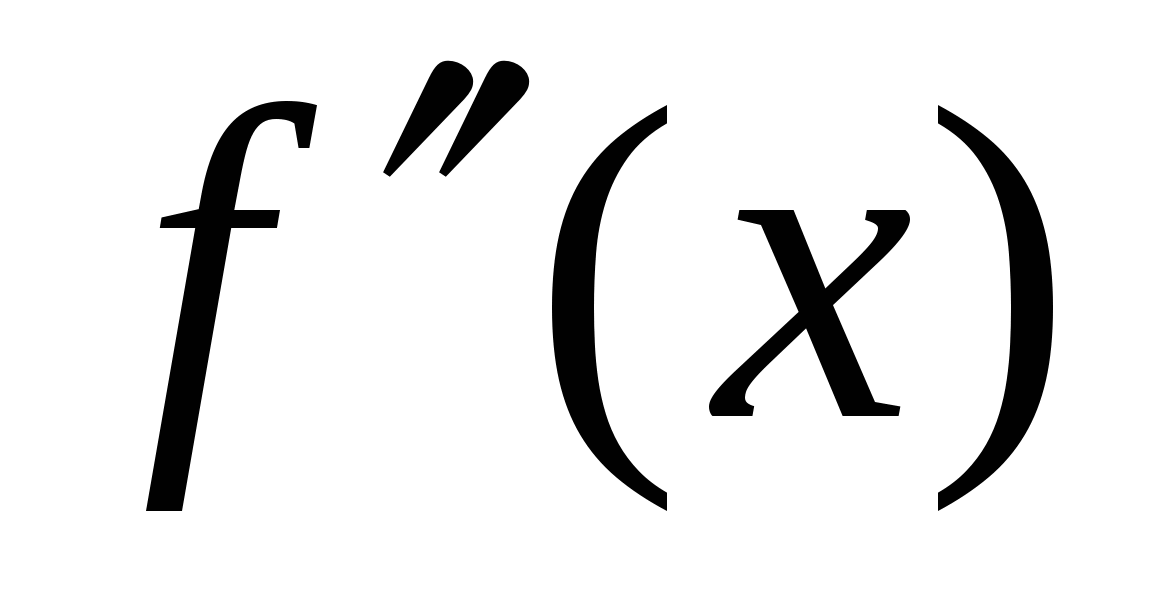 слева и справа от найденных точек и делаем вывод об интервалах выпуклости и о наличии точек перегиба. слева и справа от найденных точек и делаем вывод об интервалах выпуклости и о наличии точек перегиба.
Находим значение функции в точках перегиба.
Найти точки пересечения графика с осями координат и, если это нужно для схематического построения графика, найти дополнительные точки.
Для того, чтобы найти точки пересечения графика  с осью с осью 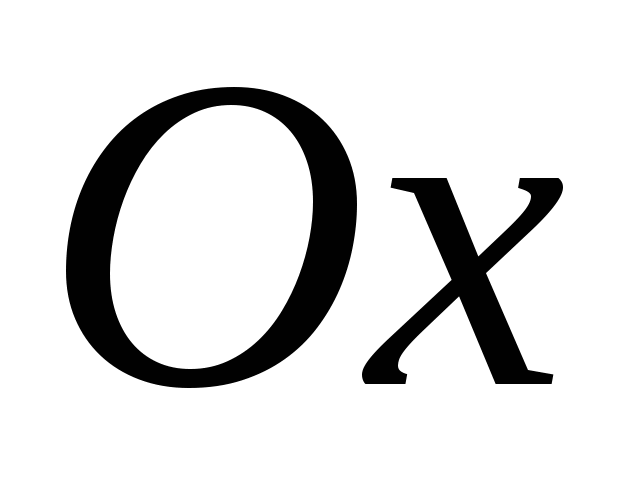 , надо решить уравнение , надо решить уравнение 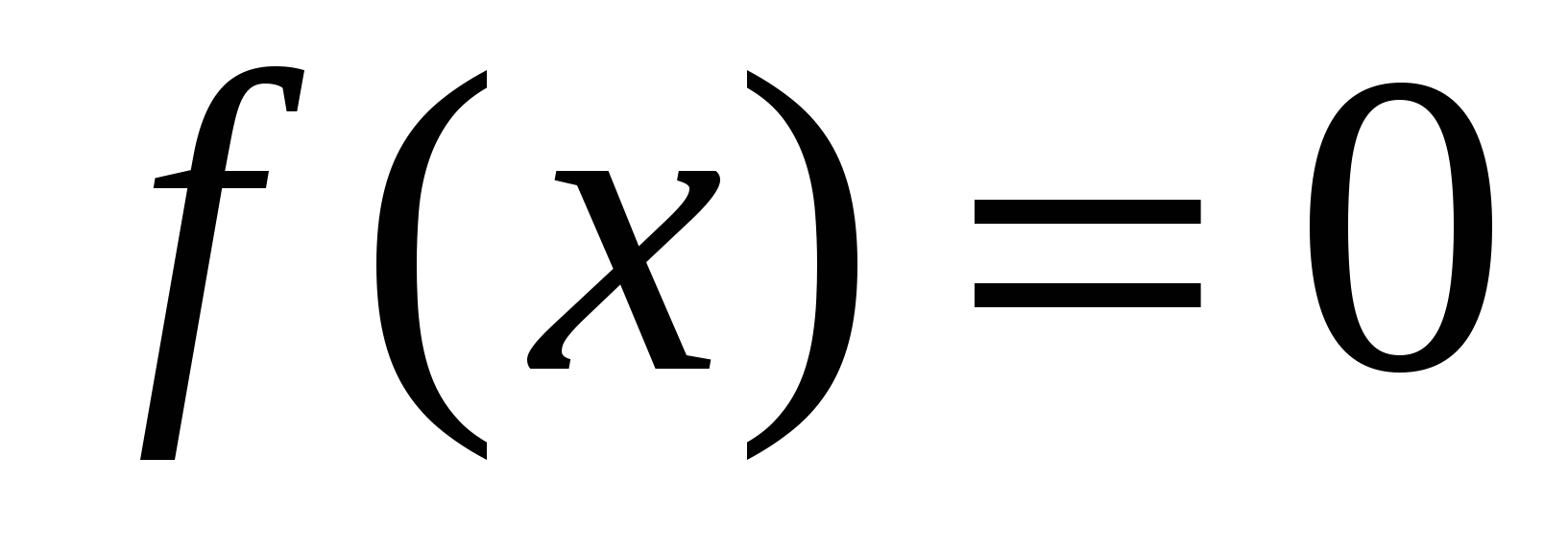 . Точки . Точки 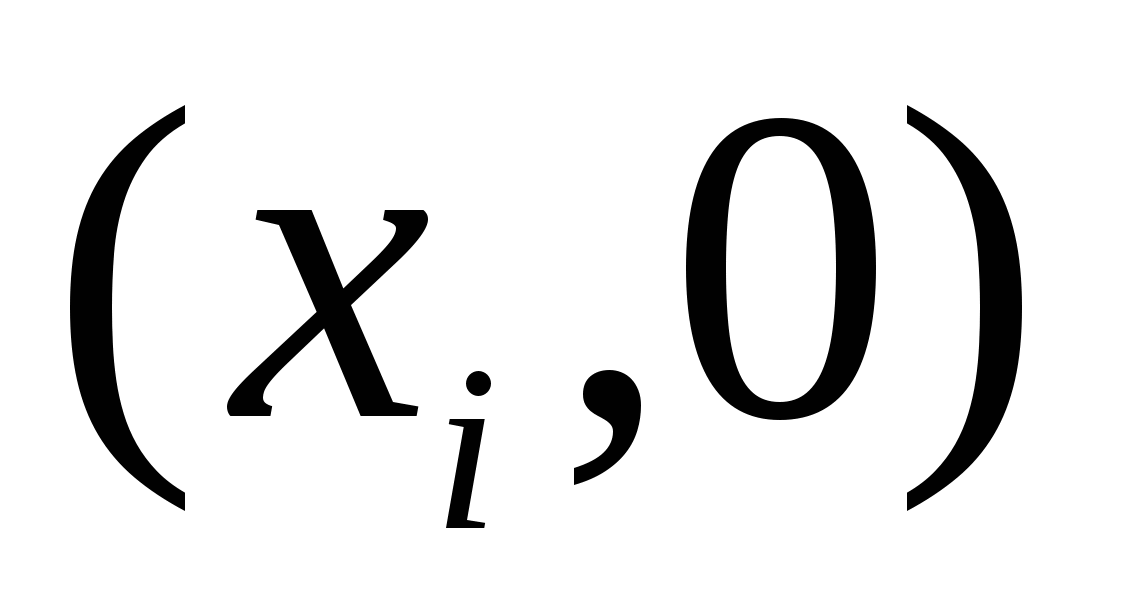 , где , где 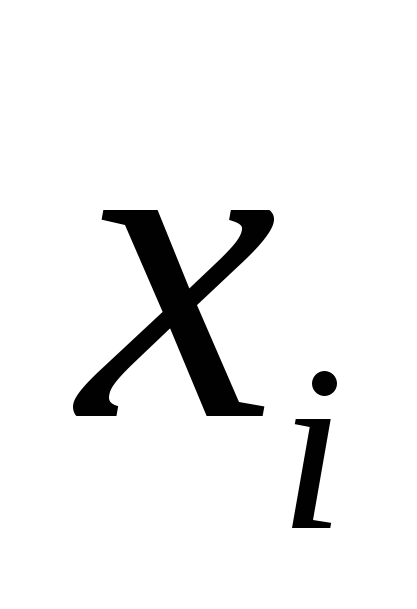 – нули – нули  , будут точками пересечения графика , будут точками пересечения графика  с осью с осью 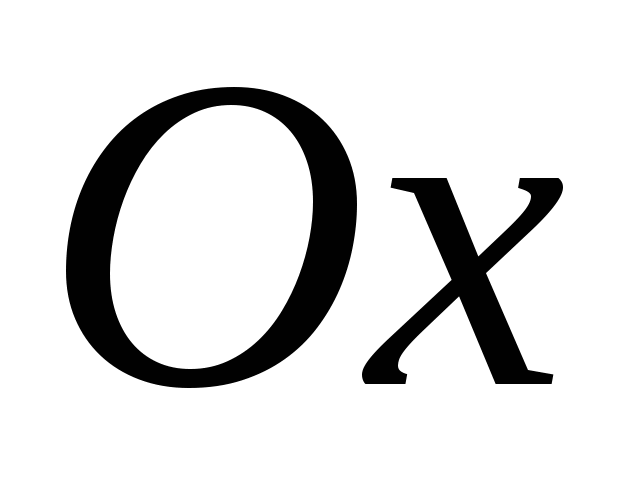 . .
Точка пересечения графика  с осью с осью 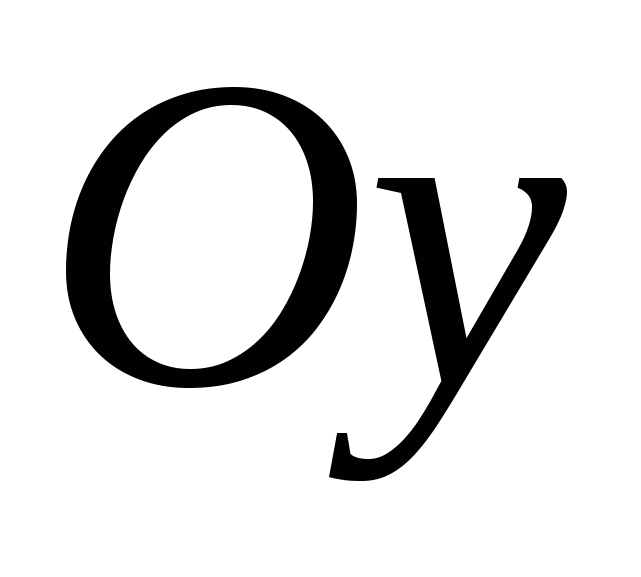 имеет вид имеет вид 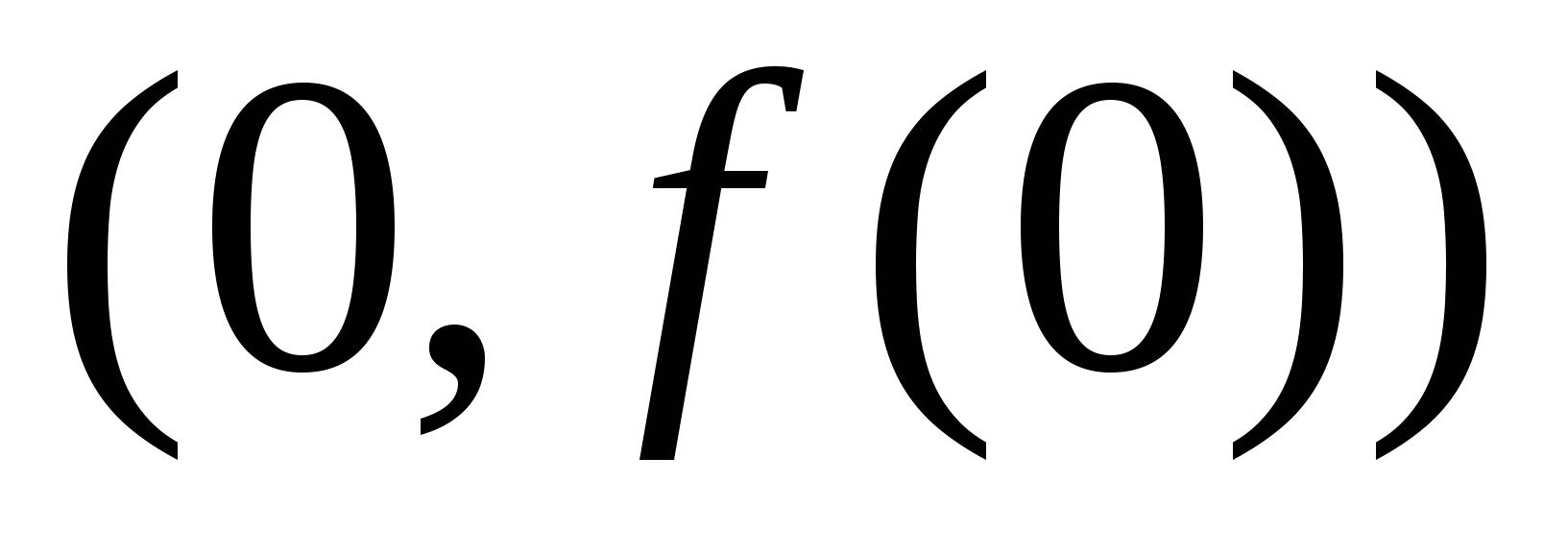 . Она существует, только если точка . Она существует, только если точка 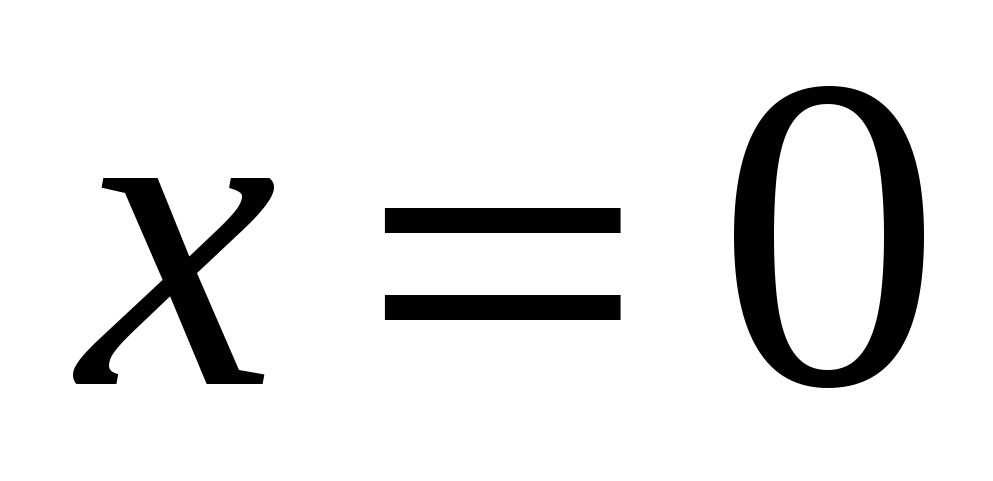 входит в область определения функции входит в область определения функции  . .
Схематично построить график.
Построить систему координат и асимптоты.
Отметить экстремальные точки.
Отметить точки перегибы и интервалы выпуклости.
Отметить точки пересечения графика с осями координат.
Схематично построить график так, чтобы он проходил через отмеченные точки и приближался к асимптотам.
Пример. Исследовать функцию 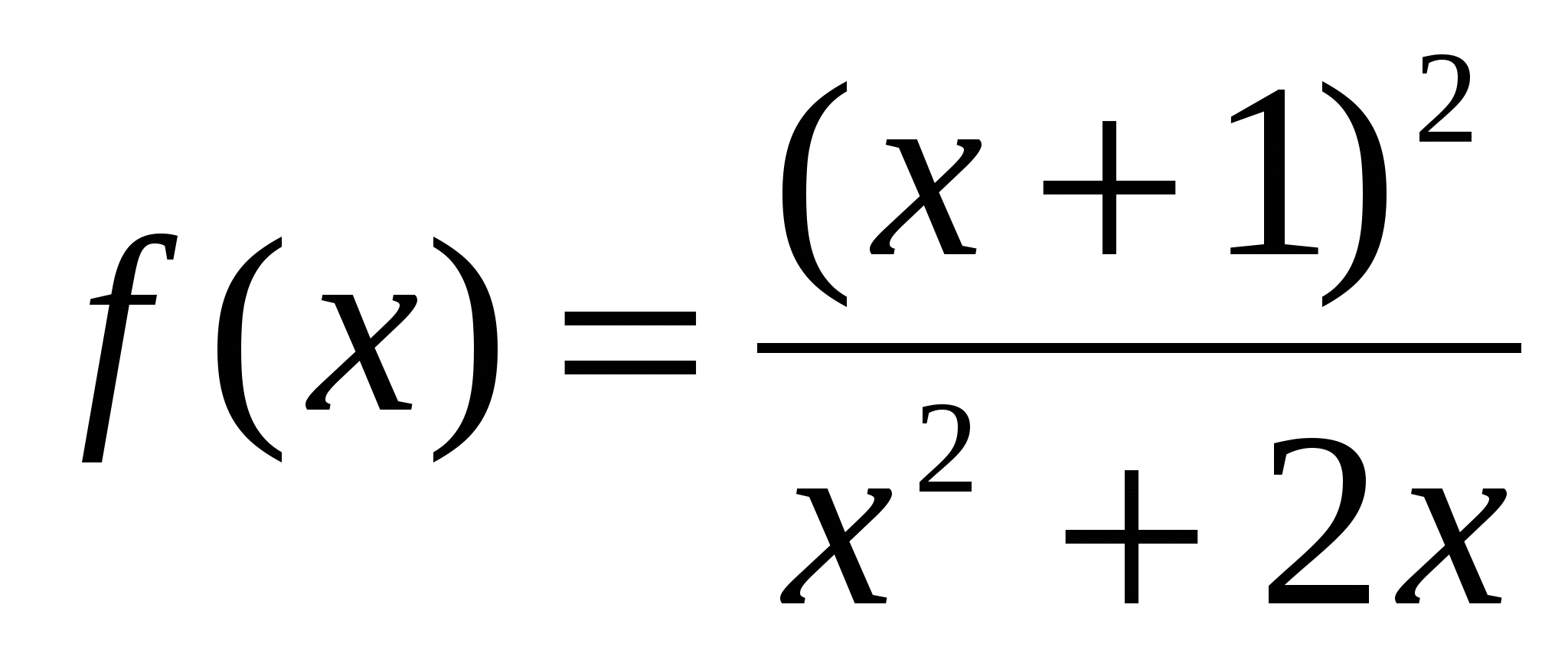 и схематично построить ее график. и схематично построить ее график.
Задания для самостоятельной работы.
Найти промежутки монотонности функций:
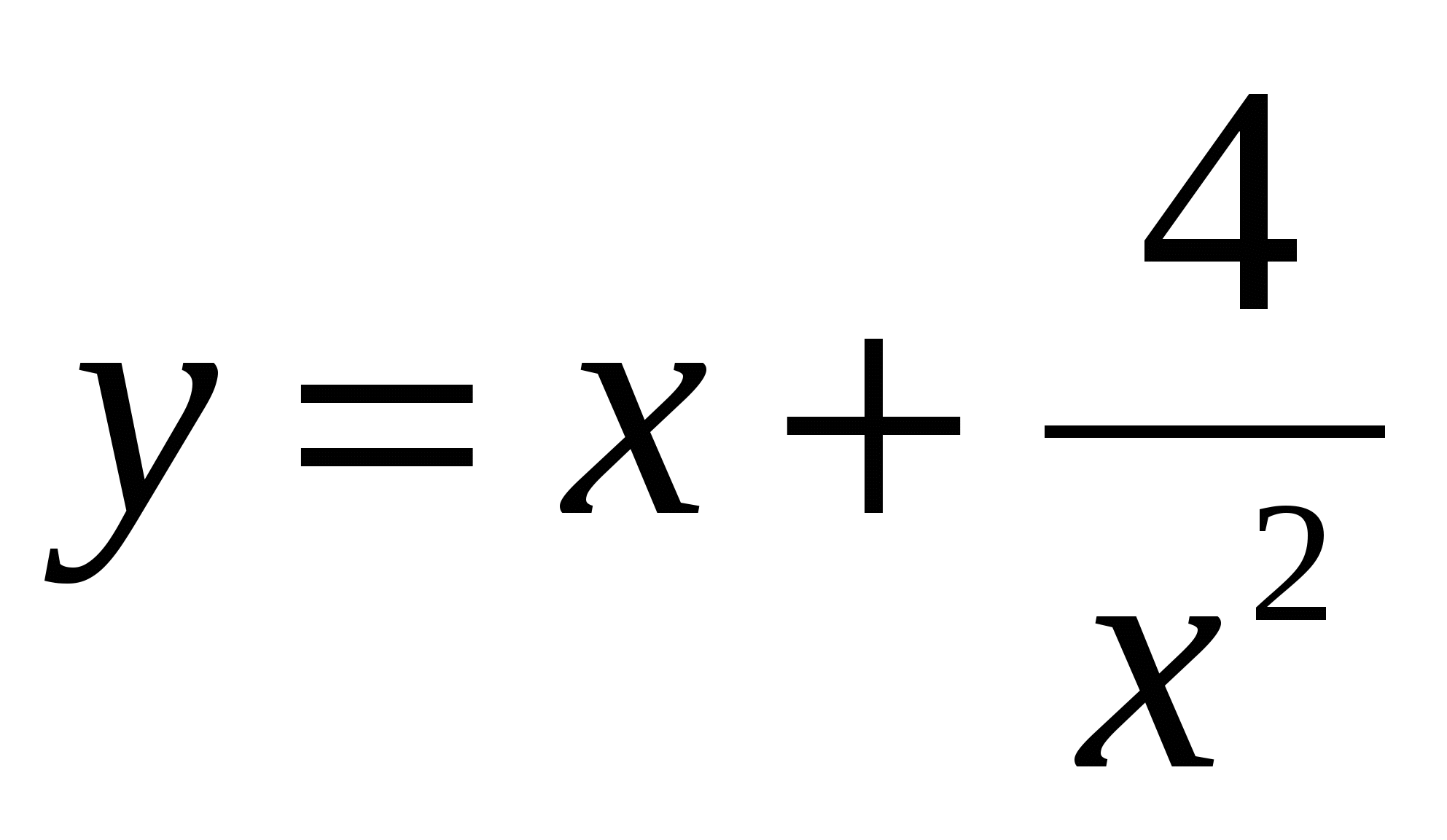 . .
|
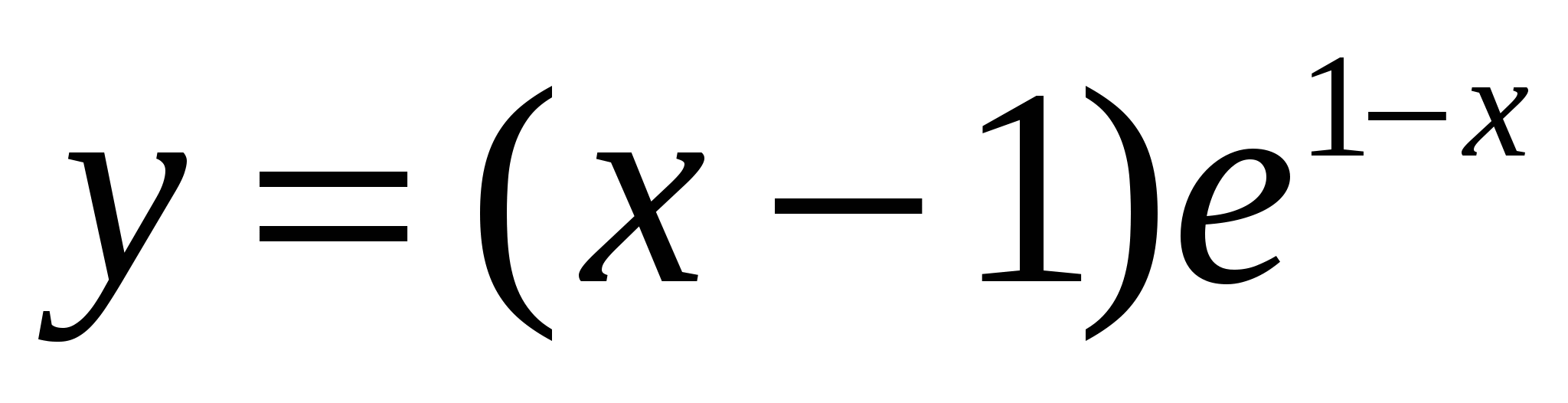 . .
|
Исследовать функции на экстремум:
Найти наибольшее и наименьшее значения каждой из функций на заданном отрезке:
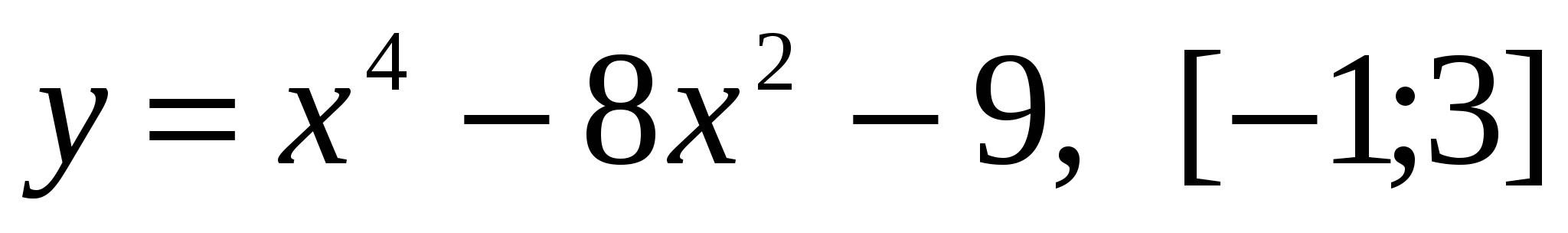 . .
|
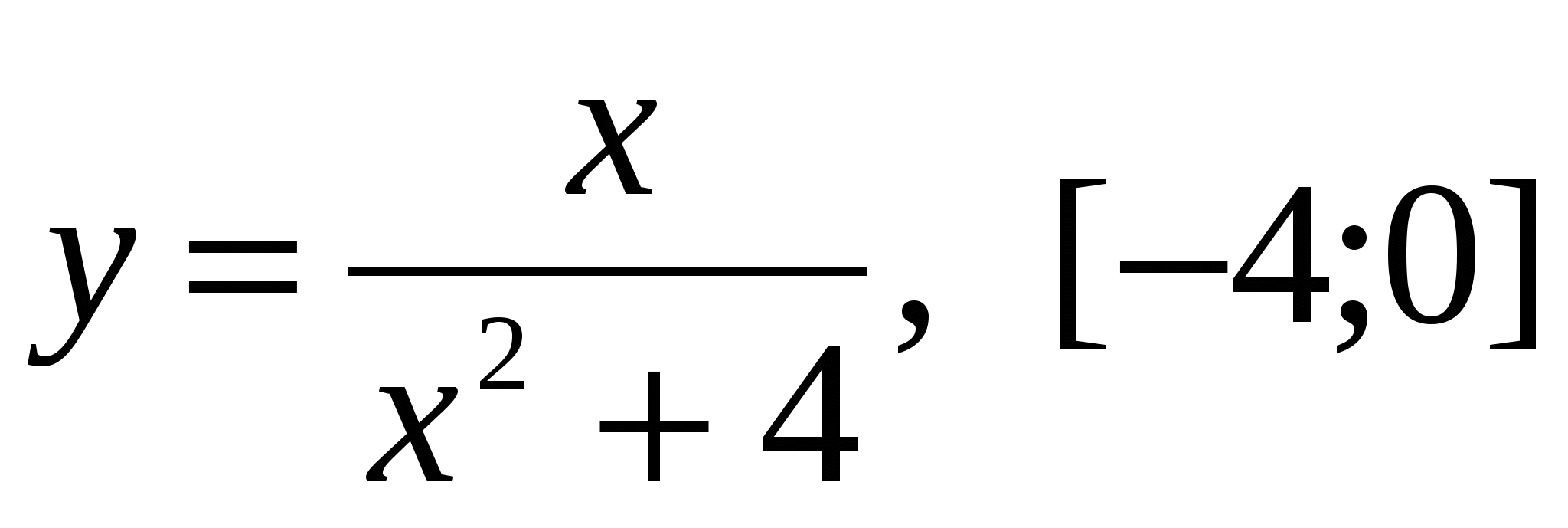 . .
|
Определить точки перегиба и интервалы выпуклости графиков функций:
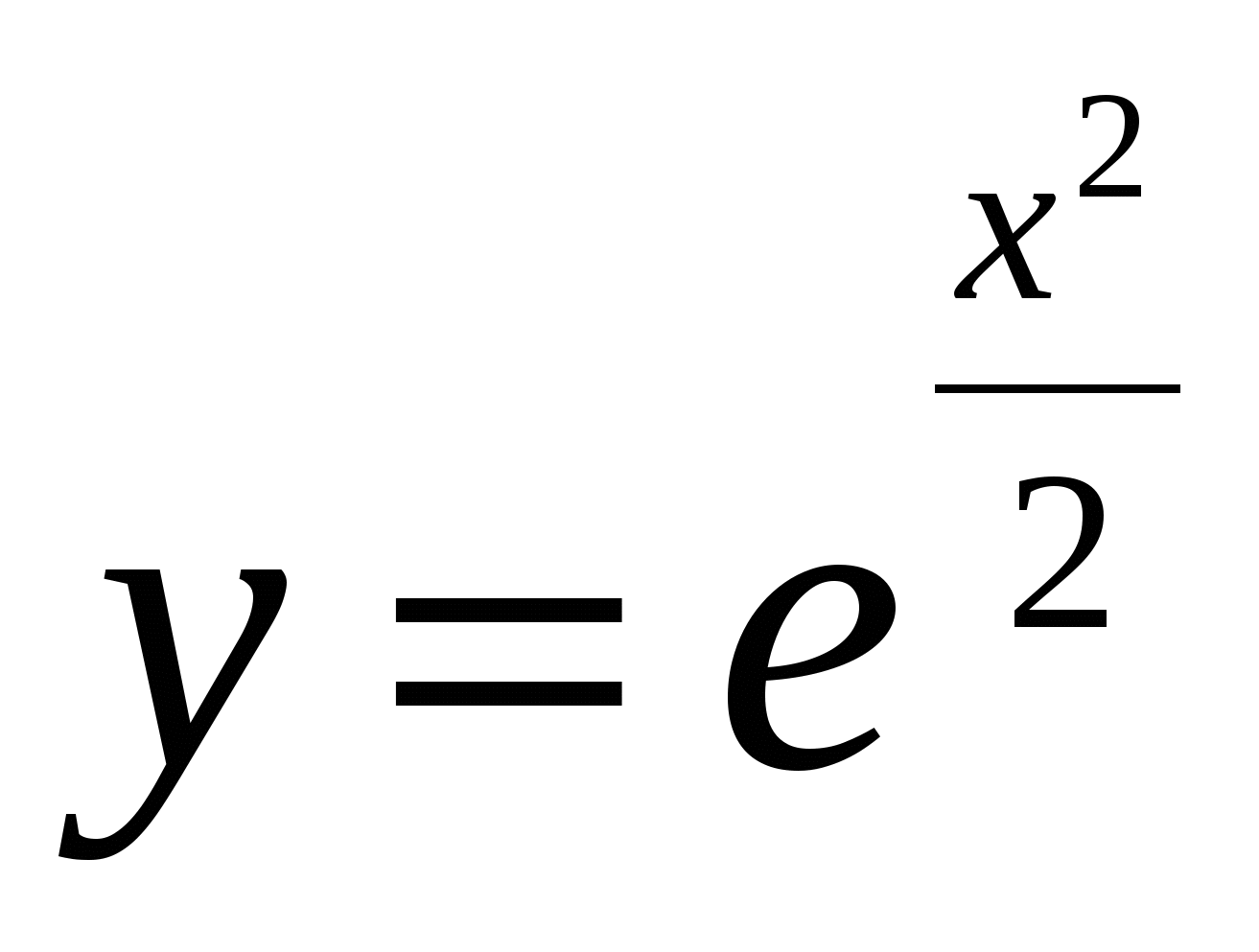 . .
|
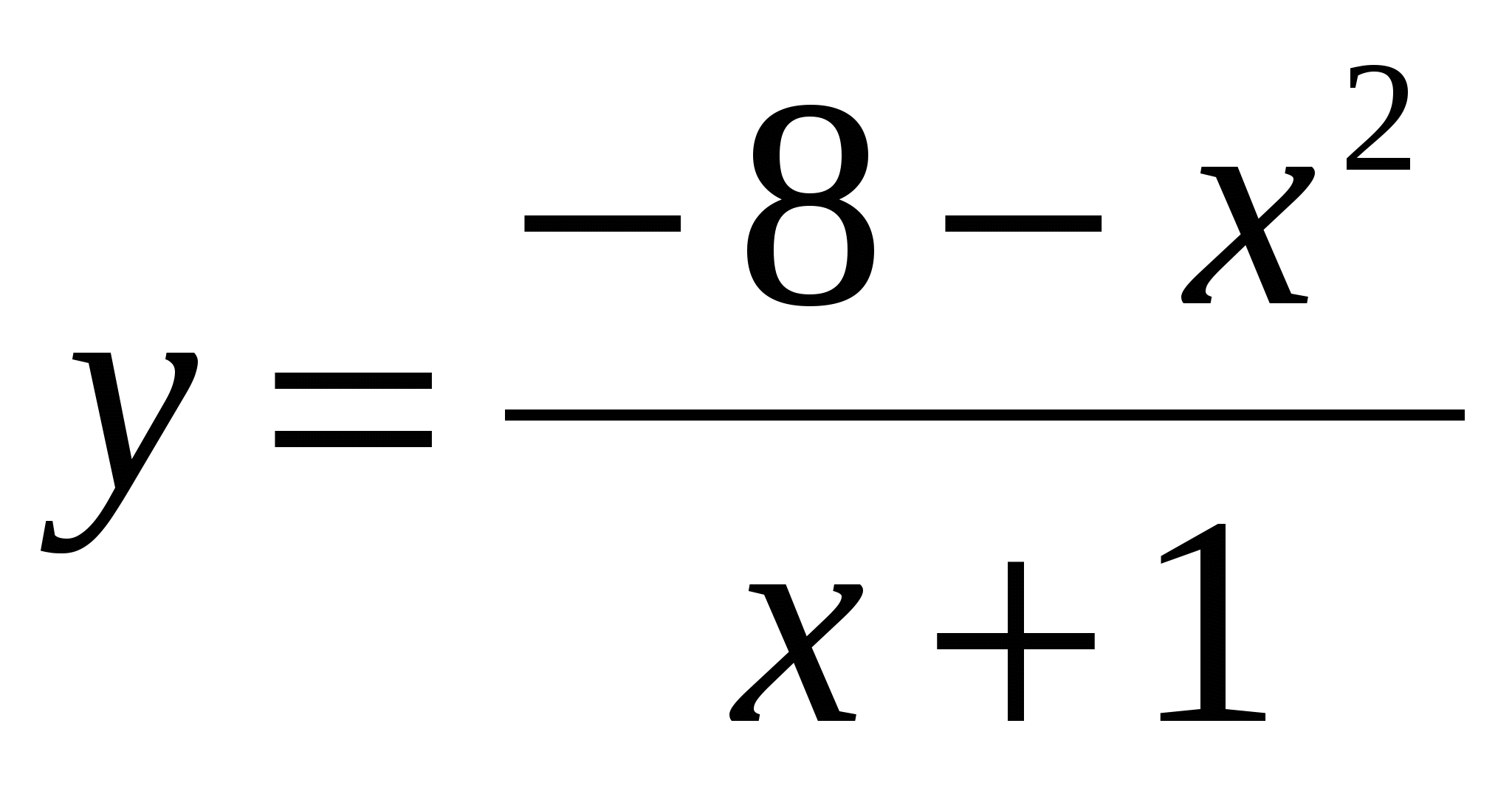 . .
|
Найти асимптоты графиков функций:
Исследовать функции и построить их графики:
|
 Скачать 0.49 Mb.
Скачать 0.49 Mb.

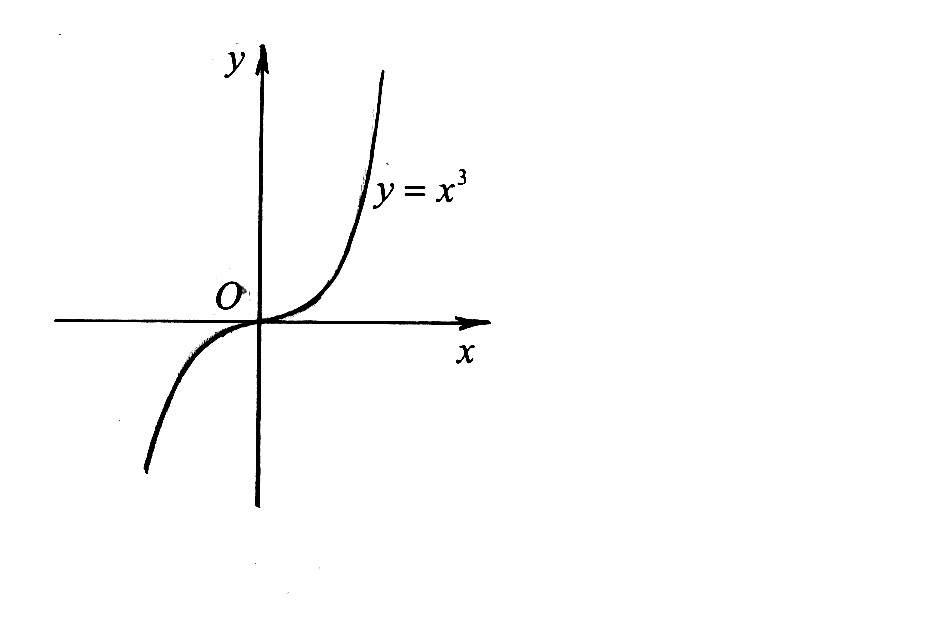
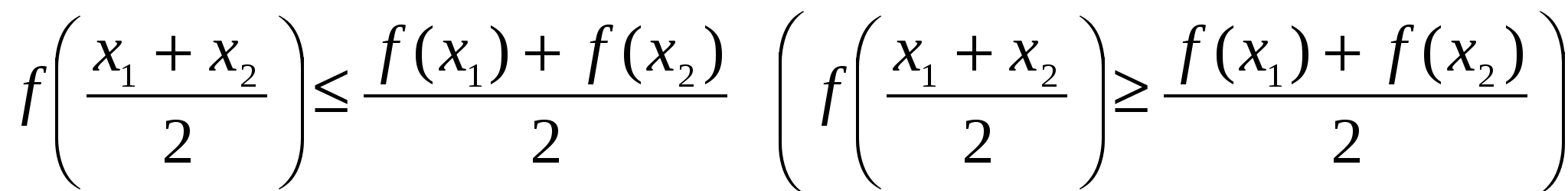 .
.
