Исследование функции. Исследование функции и построение ее графика План исследования ооф
 Скачать 50.66 Kb. Скачать 50.66 Kb.
|
|
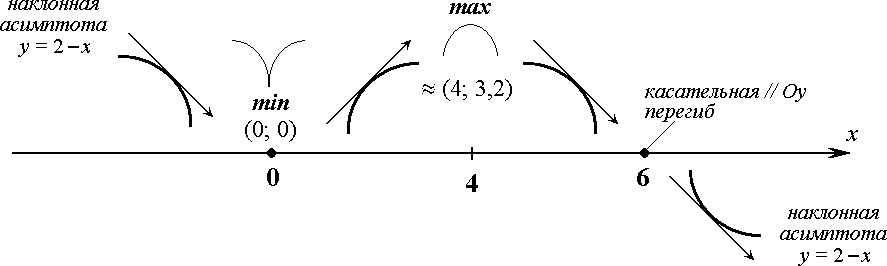
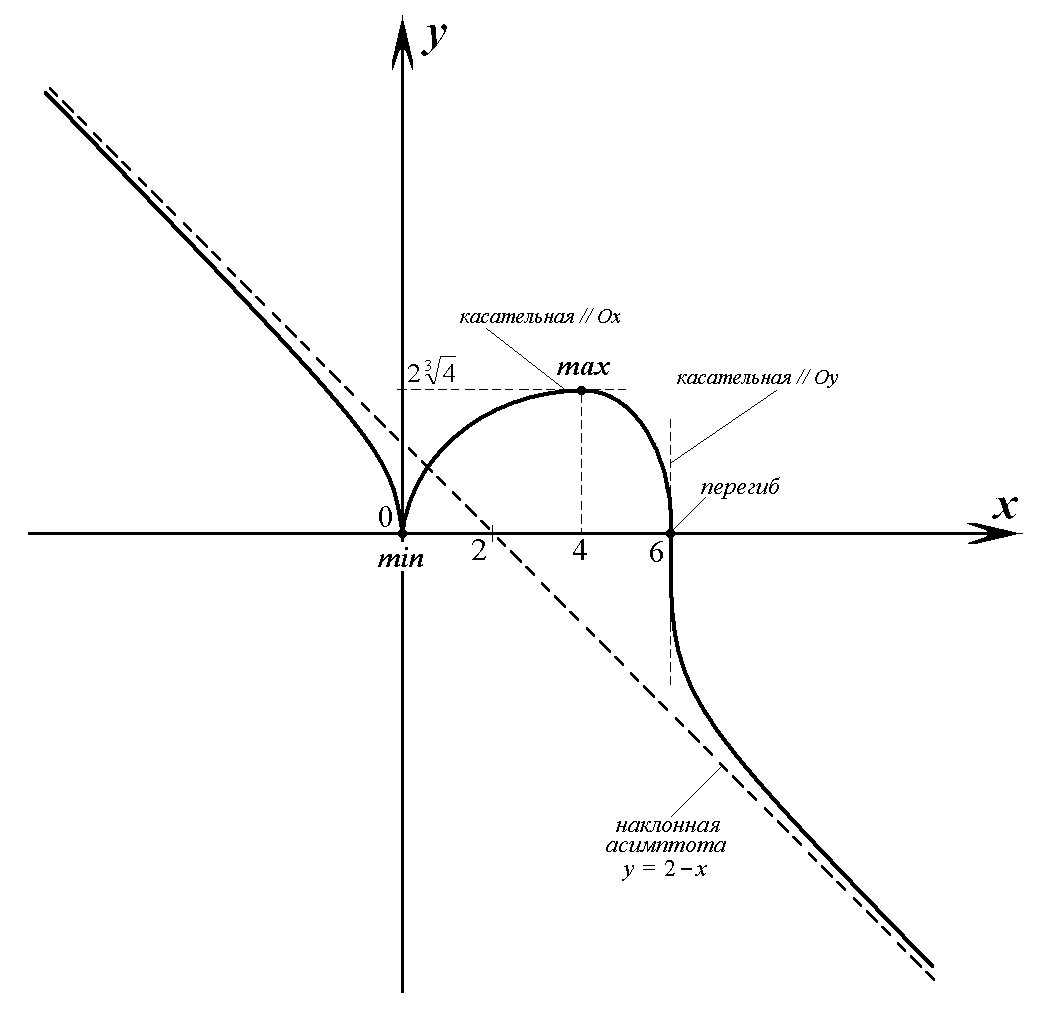
Расчетно-графическая работа № 2 Исследованиефункцииипостроениеееграфика План исследования: ООФ. Исследовать область определения функции, найти точки разрывов функции, исследо- вать функцию на вертикальные асимптоты. На вертикальные асимптоты функцию необходимо исследовать в точках разрывов и на концах области определения, если область определения ог- раничена. Особенности и симметрия функции. Исследовать функцию на четность-нечетность (и сим- метрия), периодичность. Если функция периодическая, то ее исследование можно проводить на отрезке, длина которого равно периоду. После завершения исследования построить график функции с учетом периода. Точка пересечения функции с осью Оу(при х= 0). Нулифункциииинтервалызнакопостоянства. Найти точки пересечения с осью Ох(при у = 0) и определить знаки функции в каждом из получившихся интервалов, учитывая, в том числе, и точки разрывов функции. Монотонность и экстремумы. Найти первую производную функции и определить критиче- ские точки функции первого рода, рассмотрев ситуации у′ = 0, y′ = ∞ и у′ не существует; оп- ределить знаки производной и поведение (возрастание-убывание) функции на каждом интерва- ле. Изобразить на схеме поведение функции, указав для каждой критической точки вид экстре- мума (max, min, острый, гладкий), положение касательной в точке экстремума и схематический рисунок. Найти координаты (х; у) точек экстремума. Выпуклость-вогнутость и точки перегибов. Найти вторую производную функции и опреде- лить критические точки функции второго рода, рассмотрев ситуации у′′ = 0, y′′ = ∞ и у′′ не существует; определить знаки второй производной и поведение (выпуклость-вогнутость) функции на каждом интервале. Изобразить на схеме поведение функции. Найти точки перегиба графика функции и их координаты. Наклонные или горизонтальные асимптоты. Исследовать функцию на существование на- клонных асимптот. При исследовании обязательно указывать, при каких значениях х(х → +∞; х→ ∞ или х→ ±∞) данная прямая является асимптотой функции. При отсутствии наклон- ных асимптот необходимо исследовать поведение функции при x . Дополнительные точки. В том, и только в том случае, когда исследуемая функция не имеет критических точек в пп. 4, 5 и 6, необходимо найти несколько дополнительных точек для по- строения графика функции — по одной дополнительной точке для каждой ветви графика. Замечание: дополнительных точек не должно быть много, так как график функции должен быть построен по ее исследованию, а не по точкам. Функции, построенные по точкам, на проверку не принимаются. Эскиз графика функции. Построить эскиз графика функции, учитывая результаты исследо- ваний, критические точки и асимптоты. Для облегчения решения задачи можно изобразить итоговую схему поведения функции. Замечание1: при оформлении работы каждый пункт должен быть оформлен отдельно и содер- жать вывод, причем пп.4, 5 и 6 — в виде схемы. Замечание2: все критические точки, положение касательной в точках экстремума, асимптоты и т.д. должны быть отмечены на графике. Пример. Исследовать функцию y и построить ее график. 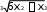 ООФ. х R, функция непрерывна, вертикальных асимптот не имеет. ООФ. х R, функция непрерывна, вертикальных асимптот не имеет.Четность-нечетность,периодичность. Данная функция непериодична. Исследуем ее на чет- ность-нечетность. Найдем 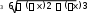 f(x) f(x) f(x) : 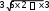 , f( x) , f( x) f(x), f(x) f(x) 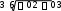 функция общего вида, симметрией не обладает. функция общего вида, симметрией не обладает.ПересечениесОу.f(0) 0 имеем точку (0; 0). Нули функциииинтервалызнакопостоянства.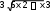 0 0 x2 (6 x) 0 х= 0, х= 6. Монотонностьиэкстремумы. Вычислим первую производную функции: 12x 3x2 4 x f(x) .   33 x4 6 x2 3 x6 x2 33 x4 6 x2 3 x6 x2Найдем точки функции, подозрительные на экстремум: 1) f(x) 0 4 x 0 x 4 — точка, в которой возможен гладкий экстремум; 2) f(x) тремум; х (6 х)2 = 0 х= 0; х= 6 — точки, в которых возможен острый экс- 3) f(x) не существует — таких точек нет. 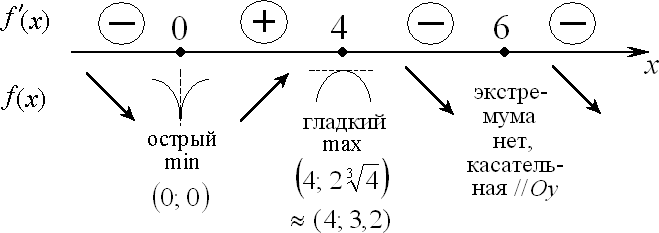 Найденные точки отметим на схеме, вычислим знаки производной в по- лученных интервалах, определим участки возрастания и убывания функции и точки экстремумов: Найденные точки отметим на схеме, вычислим знаки производной в по- лученных интервалах, определим участки возрастания и убывания функции и точки экстремумов:Выпуклость-вогнутостьиточки перегиба.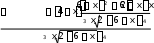 Вычислим вторую производную функции: Вычислим вторую производную функции: y = 3x6 x 4 x6 x6 3x 8   = . = .Точки, в которых возможен перегиб графика функции: 3 x4 6 x5 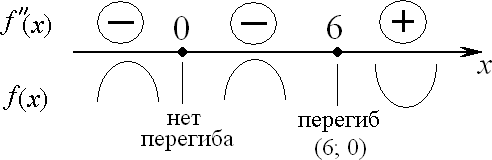 f (x) 0 — таких точек нет; 2) f (x) х= 0, х= 6; f (x) 0 — таких точек нет; 2) f (x) х= 0, х= 6;3) f (x) не существует — таких точек нет. Найденные точки отметим на схеме, вычислим знаки второй производной в полученных интер- валах, определим участки выпуклости и вогну- тости графика функции и точки перегиба: Наклонныеасимптоты. у = kx +b, 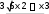 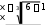 где k lim x f(x) x lim n x lim n x 1 ;  b lim f(x) kx lim 3 b lim f(x) kx lim 36x2 x3 x = lim 6x2  = =x n = lim n n  6x2 6x2 6 2 3 функция имеет наклонную асимптоту у = 2 хпри х → ± ∞. Дополнительныеточки — не требуются. |