Исследование функции и пстроить ее график
 Скачать 138.35 Kb. Скачать 138.35 Kb.
|
|
Выполнить полное исследование функции 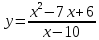 и пстроить ее график. и пстроить ее график.Решение. 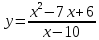 1) Найдем область определения функции 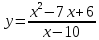 . Выражение . Выражение 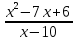 может быть вычислено при тех значениях переменной может быть вычислено при тех значениях переменной 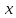 , при которых знаменатель , при которых знаменатель 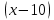 отличен от нуля: отличен от нуля: 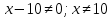 . Следовательно, область определения функции . Следовательно, область определения функции 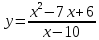 – вся числовая прямая, за исключением точки – вся числовая прямая, за исключением точки 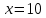 , то есть , то есть 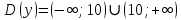 . .2) Исследуем функцию 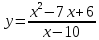 на наличие вертикальных асимптот. на наличие вертикальных асимптот.Рассмотрим интервал 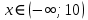 . На данном промежутке функция . На данном промежутке функция 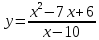 является непрерывной. является непрерывной.Рассмотрим точку 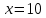 . .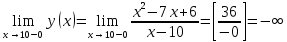 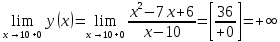 Следовательно, точка 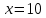 является точкой разрыва второго рода функции является точкой разрыва второго рода функции 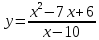 . . Рассмотрим интервал 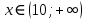 . На данном промежутке функция . На данном промежутке функция 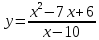 является непрерывной. является непрерывной.Таким образом, прямая 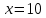 является вертикальной асимптотой графика функции является вертикальной асимптотой графика функции 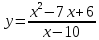 . .3) Функция 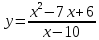 не является периодической не является периодической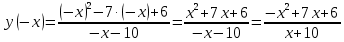 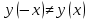 и и 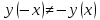 Следовательно, функция 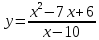 не является ни четной, ни нечетной. не является ни четной, ни нечетной.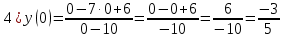 Следовательно, точка 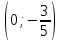 является точкой пересечения графика функции является точкой пересечения графика функции 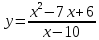 с осью ординат. с осью ординат.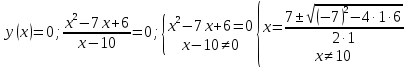 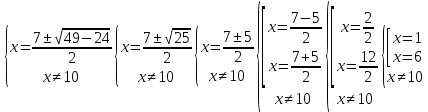 Следовательно, точки 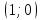 и и 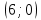 являются точками пересечения графика функции являются точками пересечения графика функции 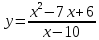 с осью абсцисс. с осью абсцисс.    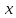          - + - + 10 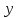 6 1 Следовательно, график функции 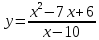 лежит выше оси абсцисс на промежутке лежит выше оси абсцисс на промежутке 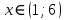 и на промежутке и на промежутке 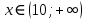 . График функции . График функции 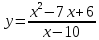 лежит ниже оси абсцисс на промежутке лежит ниже оси абсцисс на промежутке 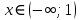 и на промежутке и на промежутке 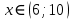 . .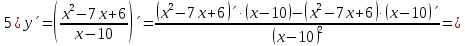 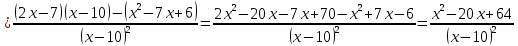 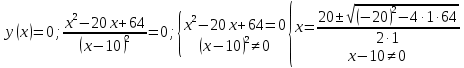 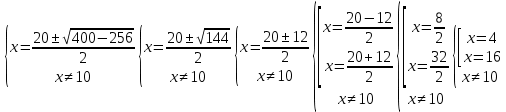  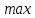 г  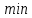 г      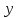     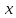          - + 16 - + 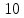 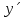 4 Функция возрастает при 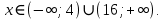 Функция убывает при 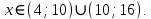 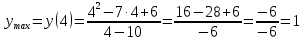 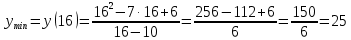 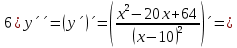 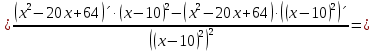 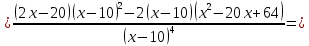 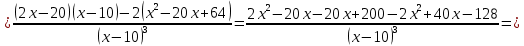 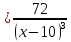 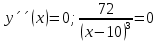 Данное кравнение не имеет решений. Следовательно, функция 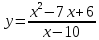 не имеет точек перегиба. не имеет точек перегиба.   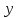   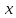      10 + - 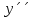 Точек перегиба нет. Функция вогнута 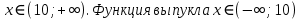 7) Исследуем функцию 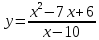 на наличие наклонных или горизонтальных асимптот. на наличие наклонных или горизонтальных асимптот.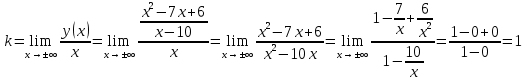 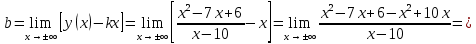 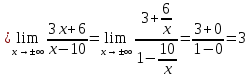 Следовательно, прямая 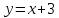 является наклонной асимптотой графика функции является наклонной асимптотой графика функции 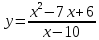 . .8) Эскиз графика функции 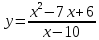 . .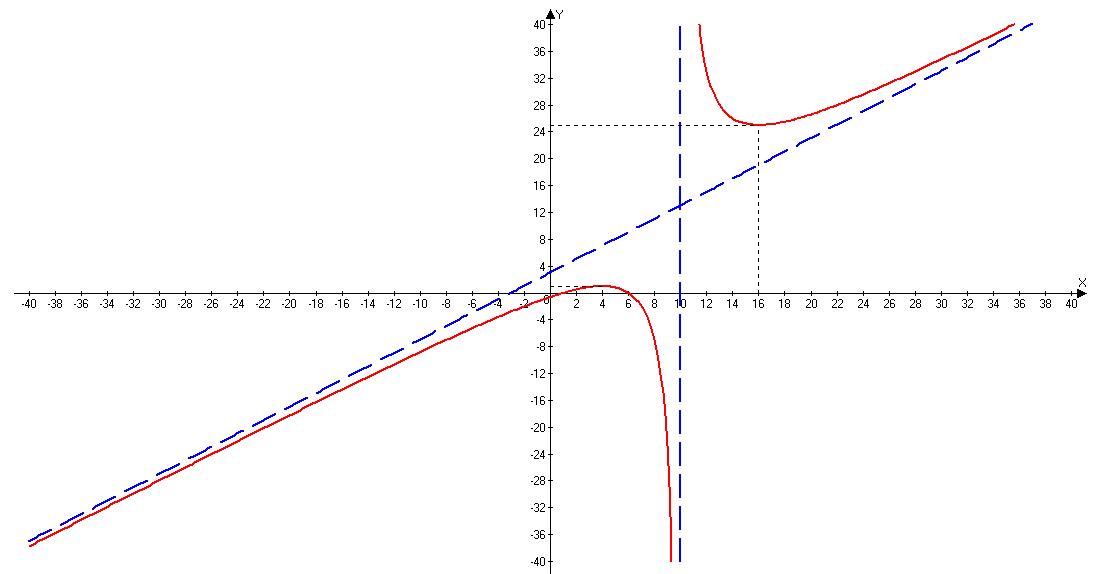 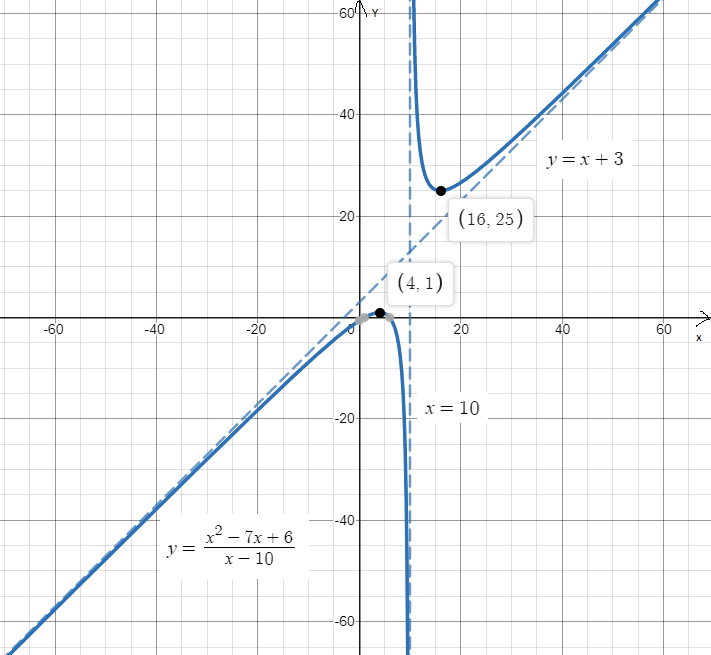 |
