Вопросы для подготовки к экзамену II курс (1). Исследование функции на монотонность. Исследование функции на экстремум с помощью первой производной
 Скачать 95.2 Kb. Скачать 95.2 Kb.
|
|
Вопросы для подготовки к экзаменам по математике Второй курс Определение комплексного числа. Алгебраическая форма комплексного числа. Геометрическая интерпретация комплексного числа. Модуль и аргумент комплексного числа. Тригонометрическая форма комплексного числа. Показательная форма комплексного числа. Предел функции. Два замечательных предела. Непрерывность функции. Формулы и правила дифференцирования. Производная сложной функции, высших порядков. Частные производные. Общая схема исследования функций. Исследование функции на монотонность. Исследование функции на экстремум с помощью первой производной. Исследование функции на экстремум с помощью второй производной. Исследование функции на направление выпуклости и точки перегиба. .Табличные интегралы. Методы интегрирования функций. Определенный интеграл. Методы интегрирования. Дифференциальные уравнения первого порядка с разделенными и разделяющимися переменными. Общее и частное решение дифференциальных уравнений. Числовые ряды. Необходимый признак сходимости ряда. Достаточные признаки сходимости рядов с положительными членами. Знакочередующиеся и знакопеременные ряды. Признак сходимости Лейбница для знакочередующихся рядов. Решение систем линейных уравнений. Формулы Крамера. Метод Гаусса. Элементы комбинаторики. Сочетания. Размещения. Перестановки. Случайные события. Вероятность события. Матрицы. Действия над матрицами. Примерные практические задания: Вычислите неопределенный интеграл: а)  ; б) ; б) В ящике находится 5 белых и 9 черных шаров. На удачу вынимают одновременно два шара. Найдите вероятности того, что оба шара окажутся белыми. Составьте уравнение касательной к графику функции 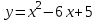 в точке с абсциссой x=4. в точке с абсциссой x=4. Вычислите предел: а) 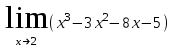 ; б) ; б)  Решите дифференциальное уравнение: а) 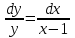 ; б) ; б)  =y =yТело движется прямолинейно со скоростью  (V-м/c) . Найдите расстояние, пройденное телом за 3-ю секунду. (V-м/c) . Найдите расстояние, пройденное телом за 3-ю секунду.Вычислите объем тела, образованного при вращении вокруг оси ОХ фигуры, ограниченной линиями:  Найдите производные функции: а)  Вычислить площадь фигуры, ограниченной линиями: а)  б)  и осью ОХ и осью ОХНайти частные производные: а)  при х = -1, б) при х = -1, б)  при х = 4 при х = 4Экзаменационные билеты пронумерованы от 1 до 35. Какова вероятность того, что наудачу взятый билет имеет номер, кратный либо 5,либо 7, либо обоим одновременно. Выполните действие над комплексными числами в алгебраической форме:  , если , если  Билеты пронумерованы двухзначными числами. Наудачу берут один билет. Какова вероятность того, что номер билета состоит из одинаковых цифр?  ; ;  ). Найдите ). Найдите 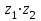 Материальная точка движется по закону  (м). Найдите её ускорение в конце 3-ей секунды. (м). Найдите её ускорение в конце 3-ей секунды.Решите систему линейных уравнений: а)  ; б) ; б)  Представьте комплексное число  в тригонометрической и показательной формах. в тригонометрической и показательной формах. Выполните действие в алгебраической форме: а) (-2+3i) – (7-2i); б) 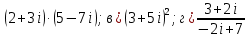 Найдите наибольшее и наименьшее значение функции  на на  В момент времени t тело находится на расстоянии 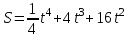 (км) от места отправления. Найдите его ускорение через 2 часа. (км) от места отправления. Найдите его ускорение через 2 часа.Найдите частное комплексных чисел:  ,если ,если  , , Тело движется прямолинейно по закону  . Найдите максимальную скорость движения тела (м/с) . Найдите максимальную скорость движения тела (м/с)Решите систему линейных уравнений по формулам Крамера: а)  б)  В первой урне находится 10 белых и 2 черных шара, а во второй 4 белых и 8 черных шаров. Из каждой урны вынули по 1 шару. Найдите вероятность, что оба шара будут черными? Тело брошено вверх со скоростью  (V-м/с). Вычислите наибольшую высоту подъема тела. (V-м/с). Вычислите наибольшую высоту подъема тела.Решить уравнение:  . .Представьте в показательной форме и выполните действия: 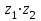 , ,  , , 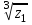 , если , если  ; ;  Представьте в показательной форме  и вычислите и вычислите 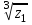 Вычислите определенный интеграл: а)  ; б) ; б)   ; ;  .Найдите: .Найдите: 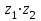 ; ; 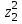 Решите систему трех линейных уравнений: 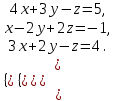 Вычислите: а)  если y = если y =  , б) , б)  , если , если 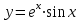 Скорость прямолинейного движения тела задана уравнением  (V-м/с). Вычислите его путь за 4 сек. (V-м/с). Вычислите его путь за 4 сек.Представьте в алгебраической и показательной формах комплексное число:  . .Вычислите пределы: а)  ; б) ; б)  Выполните действия над матрицами а) С = А2 + 2В, где А = 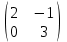 , В = , В = 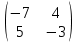 . . б)  Найдите (A-3B)(B-A) Найдите (A-3B)(B-A) 37. Постройте график сложной функции: а) 38. Исследовать функцию y= 1/3 x3 -9x на экстремум а) с помощью первой производной . б)с помощью второй производной . 39. Исследовать функцию у=х3+3х2 на направление выпуклости графика функции и точки перегиба. 40. Общая схема исследования функции и построение графика. ( у=х3+3х2) |
