ЛР тэц 2. Лаб.работы-Задание-2-ТЭЦ-2. Исследование и расчёт магнитной цепи при постоянном токе

• Название: Исследование и расчёт магнитной цепи при постоянном токе
• Анкор: ЛР тэц 2
• Дата: 12.05.2022
• Размер: 208.03 Kb.
• Имя файла: Лаб.работы-Задание-2-ТЭЦ-2.docx
• Тип: Исследование; #524363
• страница: 5 из 5

Общие сведения

В замкнутом контуре (рис. 5.5.1) после отключении его от источника постоянного или переменного напряжения возникает переходный процесс, обусловленный начальным запасом энергии в электрическом поле конденсатора и в магнитном поле катушки индуктивности. Этот процесс может носить как апериодический, так и колебательный характер.

В общем случае состояние цепи определяется из дифференциального уравнения, составленного по второму закону Кирхгофа:

Поскольку i Cdu_C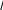


dt, то

Ri  L ^di u_Cdt
 0.

или

_RCdu_C

dt

• 
  LC
  

d²u_C

dt²

• 
  u_C
  

 0,

d²u_C

• 
  R^du_C
  

¹  

dt²

Ldt

_LCu_C 0.

t=0 _i

+
U

_R L
^uC _C

-
Рис. 5.5.1.
Вид решения этого дифференциального уравнения зависит от характера корней характеристического уравнения:

Корни этого уравнения:

p²  ^Rp ¹

L LC
 0.

^R  ^R^{2 1}

^p12

^{  }   ^{ .}

2L 2L LC

 

 ^R^{2 1}

Когда

 _2L

  0,т .e. R  2

LC

 R_кр, корни вещественные

 

отрицательные и процесс изменения тока и напряжений имеет апериодический ^{затухающий характер (рис. 5.5.2а). Если же R}кр^{, то возникает колебательный процесс} (рис. 5.5.2б). Тогда решение дифференциального уравнения имеет вид:

u_C

u₀

sin ψ

e^δtsin ωt ψ;
R

i ^u0

ωL

e^δtsint,

где

δ , ω .

2L

0

0

Рис. 5.5.2.
^{При уменьшении сопротивления от некоторого значения, большего, чем R}кр сначала увеличивается скорость затухающего апериодического процесса, затем, при ^R=Rкр ^{качественно изменяется характер процесса – он становится колебательным - и при} дальнейшем уменьшении сопротивления увеличивается частота колебаний и уменьшается затухание. При R, стремящемся к нулю, частота стремится к резонансной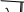

частоте ω₀  1 _LC, а затухание  – к нулю.

^{В данной работе заряд конденсатора до напряжения u}0 ^{осуществляется} однополярными прямоугольными импульсами напряжения и исследуется процесс его разряда на сопротивление и индуктивность во время пауз между импульсами. Повторяющийся процесс заряда и разряда конденсатора можно наблюдать на электронном или виртуальном осциллографе.

Экспериментальная часть

Задание

Исследовать влияние активного сопротивления на характер процесса разряда конденсатора на сопротивление и индуктивность. Сравнить экспериментальные частоту и затухание колебаний с расчётными значениями.

Порядок выполнения работы

• 
  Измерьте омметром и запишите активное сопротивление катушки индуктивности, указанной на схеме (рис. 5.5.3):
  

^Rк^{= Ом.}

• 
  Вычислите резонансную частоту и критическое сопротивление колебательного контура: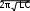
  

f₀  ¹ 

Гц;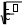

R_кр 2

Ом;

• 
  Соберите цепь согласно схеме (рис. 5.5.3), выведите подстроечный резистор Rдоб на ноль и установите на источнике напряжения однополярные прямоугольные импульсы частотой 200 Гц и максимальной амплитуды.
  

R_доб.=1 кОм

^R_K L=33 мГн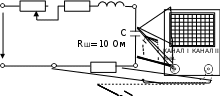

U=10 B

m

f=0,2 кГц

Рис. 5.5.3.

• 
  ^{Настройте осциллограф для наблюдения кривых u}C^{(t) и i(t) (наиболее удобная я} развёртка 200 - 500мкС/дел.).
  
• 
  Определите по осциллографу период затухающих колебаний и вычислите частоту:
  

T= мС, f= Гц.
Убедитесь, что полученное значение частоты близко к резонансной частоте.

• 
  ^{Плавно увеличивая добавочное сопротивление R}доб^{, убедитесь, что частота} колебаний слегка уменьшается, а затухание увеличивается и при большом сопротивлении процесс становится апериодическим.
  
• 
  Установите регулятор потенциометра в положение, при котором процесс меняет характер, отключите питание и измерьте омметром добавочное сопротивление:
  

^Rдоб^{= Ом.}

• 
  Вычислите суммарное активное сопротивление колебательного контура:
  

^RШ^+Rдо^б+Rк^{= Ом}

^{Убедитесь, что эта сумма близка к R}кр^.