Тоат курсовая. ТОАТ 35 2022. Исследование кодирующего и декодирующего устройств с использованием программы ElektronicsWorkbench

• Название: Исследование кодирующего и декодирующего устройств с использованием программы ElektronicsWorkbench
• Анкор: Тоат курсовая
• Дата: 23.12.2022
• Размер: 0.49 Mb.
• Имя файла: ТОАТ 35 2022.docx
• Тип: Исследование; #860929

Содержание

Введение…………………………………………………………………………….3

1 Задание и исходные данные по варианту задания……………………………..5

2 Результаты выполненного задания на курсовую работу………………………8

2.1 Построение кода для передаваемого сообщения……………………...8

2.2 Расчет корректирующих способностей заданного кода………….…...9

2.3 Структурный синтез кодирующего устройства (кодера)……………..9

2.4 Структурный синтез декодирующего устройства (декодера)……….11

2.5 Исследование кодирующего и декодирующего устройств с использованием программы ElektronicsWorkbench……………………...12

Вывод………………………………………………………………………………27

Список использованной литературы………………………………...…………..28

Введение

В настоящее время на железнодорожном транспорте всё более широкое применение получают цифровые системы автоматики и телемеханики, в которых информация передается в виде определенной кодовой комбинации. Цифровые методы передачи информации по сравнению с другими обладают рядом преимуществ, например:

а) прием сигнала сводится к обнаружению логических сигналов «1» или «0»;

б) сообщения в цифровой форме относительно легко подвергаются

обработке, записи, коммутации и регистрации;

в) возможна многократная передача данных без накопления ошибок;

г) применение помехоустойчивого кодирования позволяет значительно увеличить достоверность передачи телемеханических сообщений;

е) улучшается использование канала связи в случае применения специальных кодов, статистически согласованных с передаваемыми сообщениями.

Процесс преобразования сообщения для передачи по каналу связи средствами телемеханики называется кодированием. Процесс обратного преобразования сигнала в сообщение на приемной стороне называется декодированием.

Кодирование сообщения, которое требуется передать по каналу связи, заключается в том, что в кодовую комбинацию помимо k разрядов исходного кода (информационных разрядов) дополнительно включают r избыточных (контрольных) разрядов. В результате кодирования передаваемому сообщению будет соответствовать не k-разрядная кодовая комбинация значений исходного двоичного кода, а (k + r)-разрядное двоичное число.

Добавление контрольных разрядов в исходную кодовую комбинацию позволяет не только защитить передаваемое сообщение от возможных его искажений, но и в определенных условиях устранить искажение (восстановить информацию).

Коды, позволяющие обнаружить и исправить ошибки в кодовых комбинациях, называются помехозащищенными или корректирующими кодами. Они делятся на две группы: коды с обнаружением ошибок и коды с обнаружением и исправлением ошибок. К ним относятся такие коды как: Инверсный код (код Бауэра), Модифицированный код Бауэра, Коды Хемминга.

1 Задание и исходные данные по варианту задания

В ходе выполнения курсовой работы необходимо:

- построить заданный код для передаваемого сообщения;

- провести расчет корректирующих способностей построенного кода;

- провести структурный синтез кодирующего устройства (кодера);

- определить проверочные соотношения (синдромы) для построенного кода;

- провести структурный синтез декодирующего устройства (декодера);

- исследовать корректирующие способности синтезированного декодера при введении заданных искажений кодовых комбинаций с использованием лабораторной компьютерной программы по моделированию дискретных устройств автоматики (ElektronicsWorkbensh и/или др.);

- оформить пояснительную записку с результатами синтеза и исследований кодера и декодера информации.
Исходные данные

1) для передачи сообщений в кодовых комбинациях используем четыре информационных разряда, которые позволяют передать 2⁴= 16 возможных сообщений.

2) Кодируемое передаваемое сообщение представляет собой двоичное четырехразрядное число, получаемое преобразованием в двоичный код суммы предпоследней цифры номера зачетной книжки студента и последней цифры текущего года, т.е. 3+2 = 5 .

0101₂= 5₁₀.

3) Используемый для кодирования сообщения избыточный код выбирается по сумме двух последних цифр шифра студента из табл. 1.


Таблица 1 – Выбор варианта избыточного кода

№ п/п	Сумма чисел номера зачетной книжки	Избыточный код
3	Четное число, причем обе последние цифры шифра есть нечетные числа	Код Хемминга(семиразрядный)

Вариант 35 – Код Хемминга(семиразрядный) (так как 3 + 5 = 8, четное число, причем обе последние цифры шифра есть нечетные числа).

4)При исследовании корректирующих способностей избыточного кода на входе декодера следует сформировать следующие типы искажений кодовой комбинации:

- одиночная ошибка в информационных разрядах;

- одиночная ошибка в контрольных разрядах;

- двойная ошибка в информационных разрядах;

- двойная ошибка в контрольных разрядах;

-одиночная ошибка в информационных разрядах одновременно с одиночной ошибкой в контрольных разрядах;

- тройная ошибка в кодовой комбинации.

5) По результатам исследования кодирующего и декодирующего устройств:

- привести краткие пояснения по синтезу структурных схем кодера и декодера;

- изобразить структурные схемы кодера и декодера;

- оформить в виде таблицы результаты исследования, корректирующих способностей заданного вариантом кода;

6) Сформулировать краткие выводы по результатам выполненной курсовой работы.

2 Результаты выполненного задания на курсовую работу

2.1 Построение кода для передаваемого сообщения
Для получения семиразрядного кода Хэмминга необходимо значения младших контрольных разрядов r₁r₂r₃ определить в соответствии с аналитическими выражениями (1):

Вычислим контрольные разряды по формулам (1):

r₁=k₄⊕k₃⊕k₁=0⊕1⊕1=0

r₂=k₄⊕k₂⊕k₁=0⊕0⊕1=1 (1)

r₃=k₃⊕k₂⊕k₁=1⊕0⊕1=0
В соответствии с правилами построения кода исходная кодовая комбинация будет выглядеть следующим образом: r₁r₂k₄r₃k₃k₂k₁ = 0100101.

Значения разрядов синдрома кодовой комбинации для ее декодирования определяются по формулам (2):

i₁=r₁⊕k₄⊕k₃⊕k₁=0⊕0⊕1⊕1=0

i₂=r₂⊕k₄⊕k₂⊕k₁=1⊕0⊕0⊕1=0 (2)

i₃=r₃⊕k₃⊕k₂⊕k₁=0⊕1⊕0⊕1=0
Если комбинация значений разрядов синдрома принятой кодовой комбинации равна нулю, значит, она принята без ошибок.

2.2 Расчет корректирующих способностей заданного кода
Расчет производим для определения числа t обнаруживаемых и q исправляемых ошибок, которые могут возникнуть в процессе передачи кодовой комбинации по каналу связи. Расчет производим для каждого вида ошибок раздельно.

Число исправляемых ошибок:

q=d_min – t – 1; (3)

где d_min – минимальное кодовое расстояние, d_мин = 3 при k = 4;

t – число обнаруживаемых ошибок;

t=d_min-1=3-1=2,при q=0 (4)

t= d_min-q-1=3-1-1=1, при q=1

Вычислим по формуле (3):

q=d_min – t – 1 = 3 – 1 – 1 = 1

Из этого следует, что семиразрядный код Хемминга позволяет находить и исправлять все одиночные ошибки.

2.3 Структурный синтез кодирующего устройства (кодера)
Для синтеза схемы кодера для семиразрядного кода Хэмминга используем выражения (1) и (2) для вычисления контрольных разрядов. Структурная схема, реализующая логическую функцию сложения по модулю 2, представлена на рисунке 1(а), а ее условное обозначение - на рисунке 1(б). На рисунке 1(в) показана схема многовходового логического блока при использовании трех входов. Будем обозначать его «R». При использовании всех четырех входов – будем обозначать «I».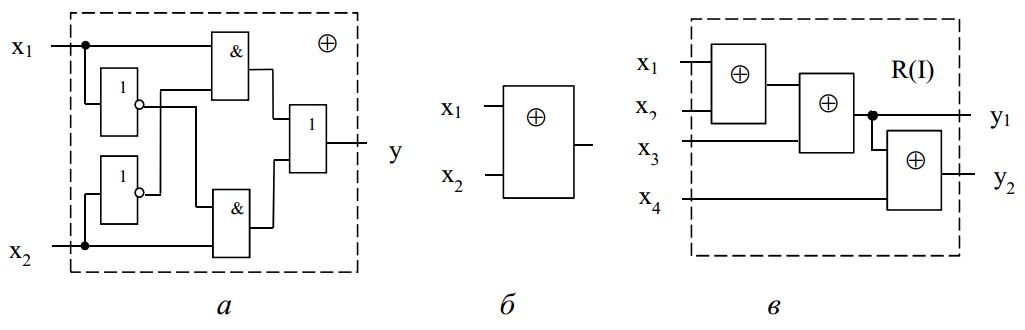



Рисунок 1 – Схемы функции сложения по модулю 2:

а - структурная схема функции сложения по модулю 2;

б - условное обозначение;

в – многовходовый блок сложения по модулю 2
Один блок R позволяет вычислить значение только одного контрольного разряда. Поэтому для построения кодера необходимо использовать три блока R по числу контрольных разрядов.

На рисунке 2 изображена схема кодера для 7-разрядного кода Хэмминга.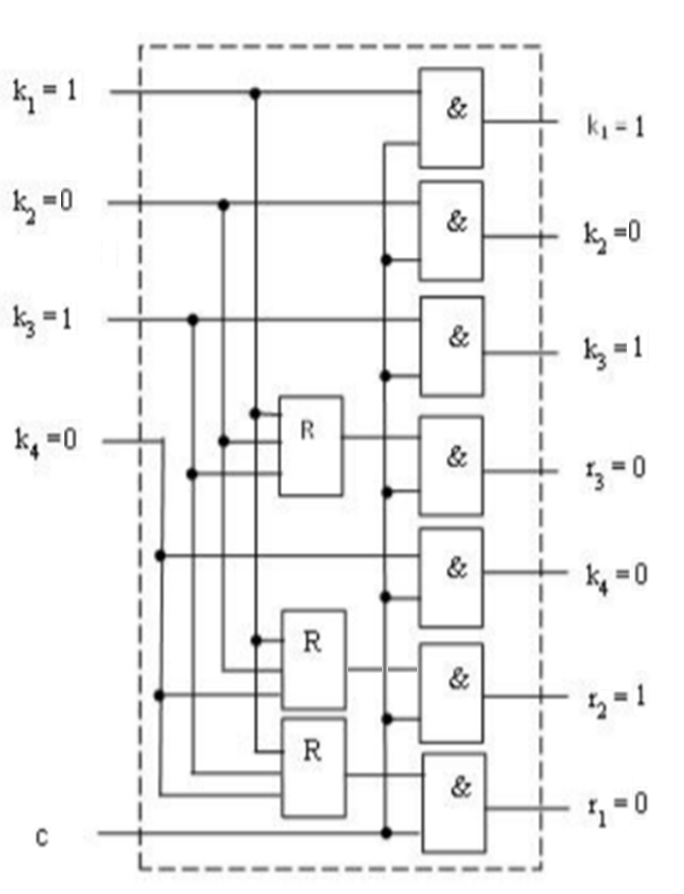

Рисунок 2 - Структурная схема кодера для 7-разрядного кода Хэмминга
Структурный синтез декодирующего устройства (декодера)

Для построения структурной схемы декодера применим логические выражения синдромов (выражение 2).

На рисунке 3 изображена схема декодера для семиразрядного кода Хэмминга.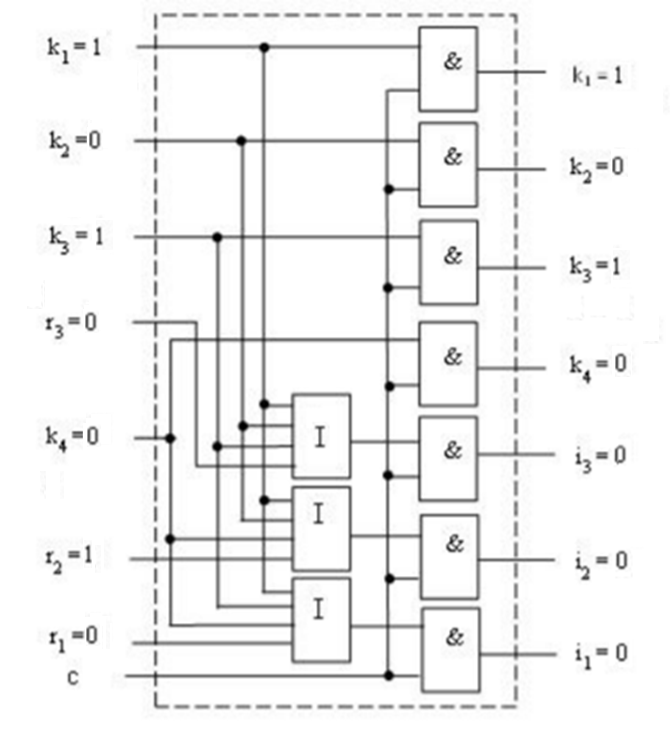



Рисунок 3 - Структурная схема декодера для семиразрядного кода Хэмминга

Исследование кодера и корректирующих свойств декодера
Исследование кодера и декодера проведем с использованием стандартной программы по моделированию устройств автоматики Elektronics Workbenсh. Используя средства программы, построим и исследуем модели кодера и декодера на типовых логических элементах.

Модель кодера и декодера представлена на рисунке 4.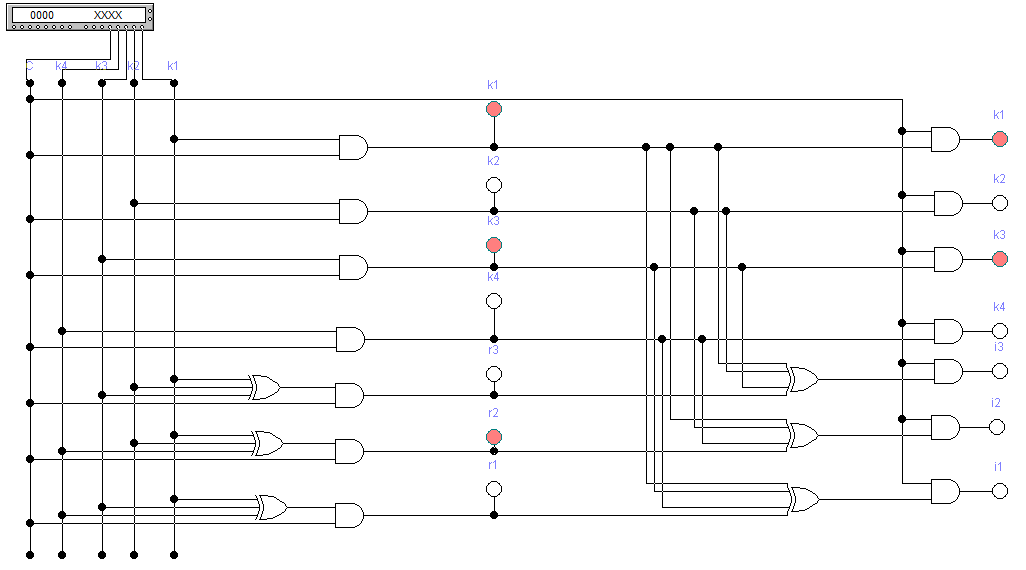


Рисунок 4 – Модель кодера и декодера в Eleсtronics Workbenсh
При исследовании корректирующих способностей избыточного кода на входе декодера сформируем следующие типы искажений кодовой комбинации:

1. 
   Одиночная ошибка в информационных разрядах (k3) – 0100001;
   
2. 
   Одиночная ошибка в контрольных разрядах (r2) – 0000101;
   
3. 
   Двойная ошибка в информационных разрядах (k4,k3) –0110001;
   
4. 
   Двойная ошибка в контрольных разрядах (r1,r2) – 1000101;
   
5. 
   Одиночная ошибка в информационных разрядах одновременно с одиночной ошибкой в контрольных разрядах(k4,r1) – 1110101;
   
6. 
   Тройная ошибка в кодовой комбинации (2 информационных k4,k3 и 1 контрольная r1) – 1110001;
   

Все исследования приведены на рисунках 5-11. Результаты исследований сведем в таблицу 3.



Рисунок 5 – Безошибочно переданное сообщение
С помощью инверторов исказим информационный разряд k₃. На вход декодера будет подаваться код r₁r₂k₄r₃k₃k₂k₁=0100001. В соответствии с логическими выражениями разряды синдрома на выходе декодера примут значения:

i₁=r₁⊕k₄⊕k₃⊕k₁=0⊕0⊕0⊕1=1

i₂=r₂⊕k₄⊕k₂⊕k₁=1⊕0⊕0⊕1=0

i₃=r₃⊕k₃⊕k₂⊕k₁=0⊕0⊕0⊕1=1
В результате на выходе декодера будет двоичное число: i₃i₂i₁=101, которое показывает, что в процессе передачи кодовой комбинации по каналу связи произошло искажение k_3.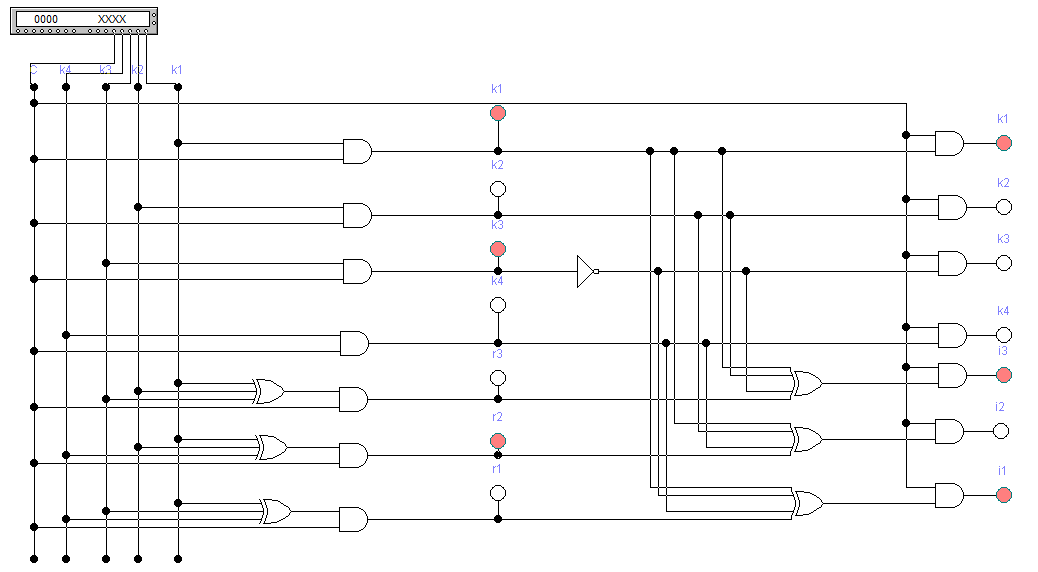


Рисунок 6 – Одиночная ошибка в информационном разряде k3
С помощью инверторов исказим контрольный разряд r₂. На вход декодера будет подаваться код r₁r₂k₄r₃k₃k₂k₁ = 0000101. В соответствии с логическими выражениями разряды синдрома на выходе декодера примут значения:

i₁=r₁⊕k₄⊕k₃⊕k₁=0⊕0⊕1⊕1=0

i₂=r₂⊕k₄⊕k₂⊕k₁=0⊕0⊕0⊕1=1

i₃=r₃⊕k₃⊕k₂⊕k₁=0⊕1⊕0⊕1=0
В результате на выходе декодера будет двоичное число: i₃i₂i₁=010, которое показывает, что в процессе передачи кодовой комбинации по каналу связи произошло искажение r_2.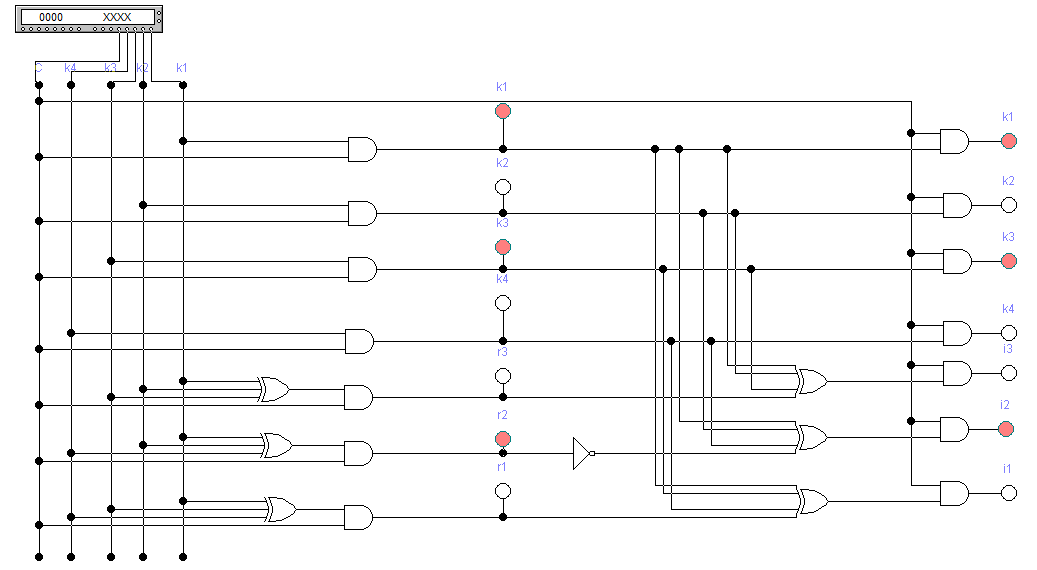


Рисунок 7 – Одиночная ошибка в контрольном разряде r2
Исказим два информационных разряда k₄ и k_3. На вход декодера будет подаваться код r₁r₂k₄r₃k₃k₂k₁=0110001.В соответствии с логическими выражениями разряды синдрома на выходе декодера примут значения:

i₁=r₁⊕k₄⊕k₃⊕k₁=0⊕1⊕0⊕1=0

i₂=r₂⊕k₄⊕k₂⊕k₁=1⊕1⊕0⊕1=1

i₃=r₃⊕k₃⊕k₂⊕k₁=0⊕0⊕0⊕1=1
В результате на выходе декодера будет двоичное число: i₃i₂i₁=110, которое показывает, что в процессе передачи кодовой комбинации по каналу связи произошло искажение в двух и более разрядах._.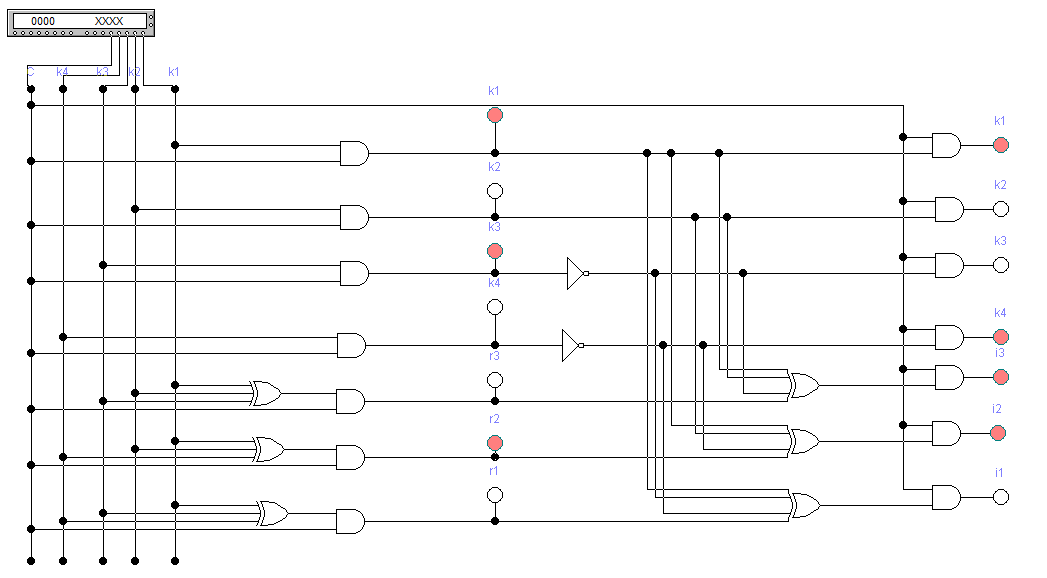

Рисунок 8 – Двойная ошибка в информационных разрядах k3,k4
Исказим два контрольных разряда r₁ и r₂._. На вход декодера будет подаваться код r₁r₂k₄r₃k₃k₂k₁=1000101.В соответствии с логическими выражениями разряды синдрома на выходе декодера примут значения:

i₁=r₁⊕k₄⊕k₃⊕k₁=1⊕0⊕1⊕1=1

i₂=r₂⊕k₄⊕k₂⊕k₁=0⊕0⊕0⊕1=1

i₃=r₃⊕k₃⊕k₂⊕k₁=0⊕1⊕0⊕1=0
В результате на выходе декодера будет двоичное число: i₃i₂i₁=011, которое показывает, что в процессе передачи кодовой комбинации по каналу связи произошло искажение в двух и более разрядах._.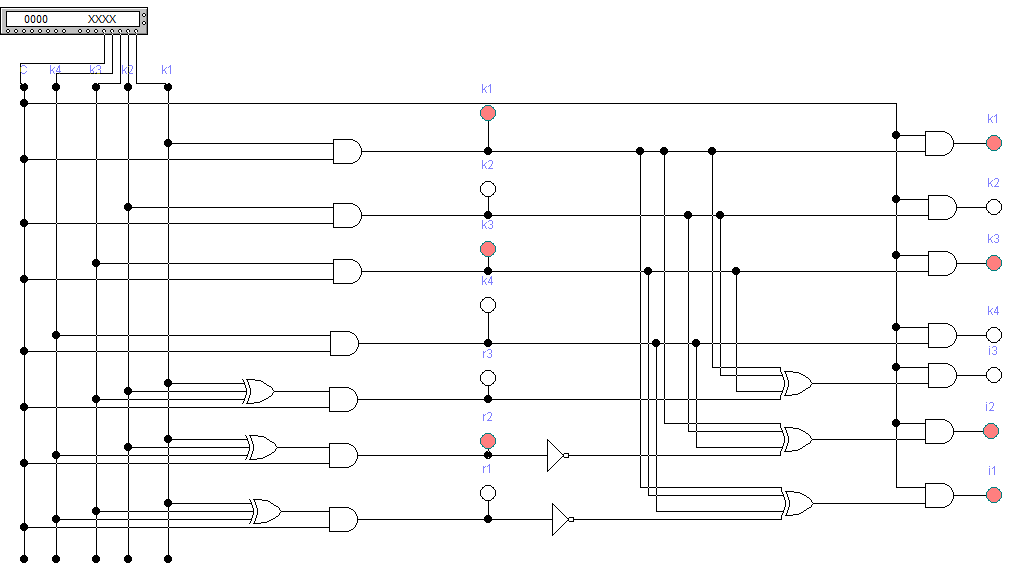

Рисунок 9 – Двойная ошибка в контрольных разрядах r1,r2
Исказим один информационный разряд и один контрольный разряд k₄ и r₁. На вход декодера будет подаваться код r₁r₂k₄r₃k₃k₂k₁=1110101. В соответствии с логическими выражениями разряды синдрома на выходе декодера примут значения:

i₁=r₁⊕k₄⊕k₃⊕k₁=1⊕1⊕1⊕1=0

i₂=r₂⊕k₄⊕k₂⊕k₁=1⊕1⊕0⊕1=1

i₃=r₃⊕k₃⊕k₂⊕k₁=0⊕1⊕0⊕1=0
В результате на выходе декодера будет двоичное число: i₃i₂i₁=010, которое показывает, что в процессе передачи кодовой комбинации по каналу связи произошло искажение в двух и более разрядах._.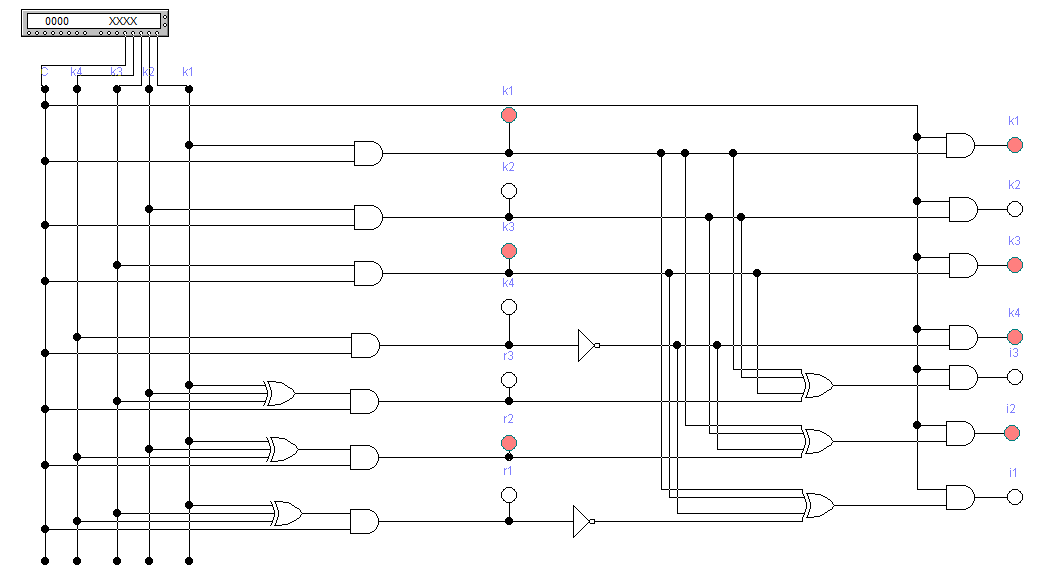

Рисунок 10 – Одиночная ошибка в информационных разрядах k4 одновременно с одиночной ошибкой в контрольных разрядах r1

Исказим два информационных разряда и один контрольный k₄, k₃ и r₁. На вход декодера будет подаваться код r₁r₂k₄r₃k₃k₂k₁=1110001. В соответствии с логическими выражениями разряды синдрома на выходе декодера примут значения:

i₁=r₁⊕k₄⊕k₃⊕k₁=1⊕1⊕0⊕1=1

i₂=r₂⊕k₄⊕k₂⊕k₁=1⊕1⊕0⊕1=1

i₃=r₃⊕k₃⊕k₂⊕k₁=0⊕0⊕0⊕1=1
В результате на выходе декодера будет двоичное число: i₃i₂i₁=111, которое показывает, что в процессе передачи кодовой комбинации по каналу связи произошло искажение. Ошибка в трех и более разрядах.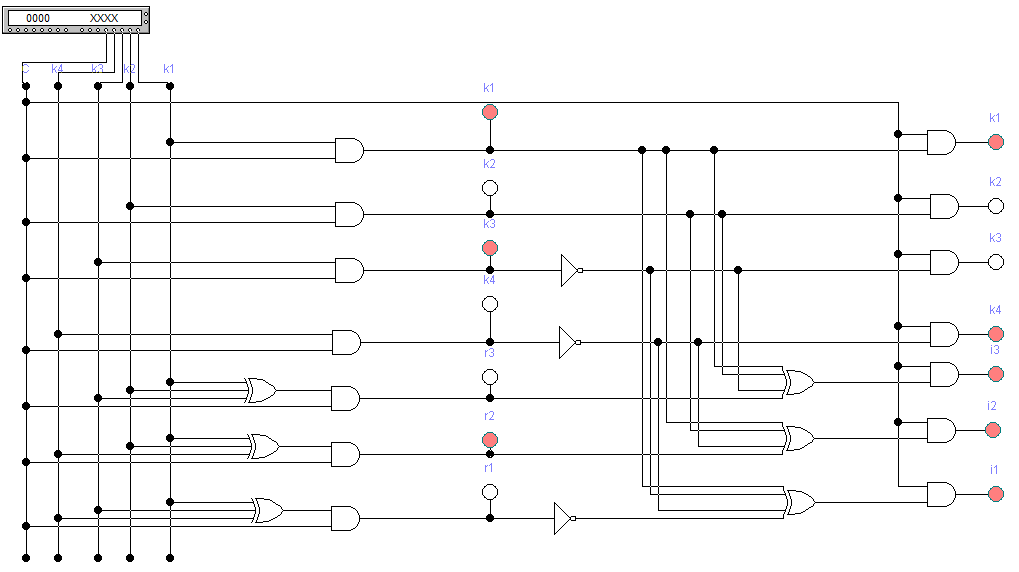




Рисунок 11 - Тройная ошибка в кодовой комбинации (2 информационных k3,k4 и 1 контрольная r1)

Таблица 3 – Результаты исследования корректирующих способностей декодера

Наименование кода
7-разрядный код Хэмминга
Номер сообщения: 5				Исходный код: 0101
Передаваемая кодовая комбинация
Принятая кодовая комбинация	Значение синдрома				Заключение
	i3	i2	i1
0100101	0	0	0		Сообщение принято без ошибок
0100001	1	0	1		Одиночная ошибка в информационном разряде k3
0000101	0	1	0		Одиночная ошибка в контрольном разряде r2
0110001	1	1	0		Неразличимая двойная ошибка
1000101	0	1	1		Неразличимая двойная ошибка
1110101	0	1	0		Неразличимая двойная ошибка
1110001	1	1	1		Неразличимая ошибка
Код позволяет обнаружить и исправить все ошибки кратностью 1. Обнаруживает ошибки кратностью 2, но не может их различить. При наличии более двух ошибок, возникает неоднозначная ситуация, при которой невозможно верно определить количество ошибок.

Вывод

В ходе курсовой работы был исследован принцип работы семиразрядного кода Хэмминга для кодирования сообщения 0101. Особенность построения кода Хэмминга заключается в том, что комбинация значений разрядов синдрома представляет собой двоичный код десятичного числа, указывающего номер разряда кодовой комбинации, в котором произошла ошибка.

При выполнении работы для кода Хэмминга были смоделированы кодер и декодер. Провели исследование корректирующей способности декодера. При исследовании выяснили, что декодер может обнаруживать и исправлять все одиночные ошибки. Обнаруживать неразличимые двойные ошибки. При наличии более двух ошибок, возникает неоднозначная ситуация, при которой невозможно верно определить количество ошибок. Это является недостатком рассмотренного семиразрядного кода Хэмминга.

Список использованной литературы

1. 
   Синтез и анализкомбинационныхустройств в системах обеспечения движения поездов : Задание и методическиеуказания для выполнения курсовойработы по дисциплине «Теоретические основы автоматики и телемеханники». – Иркутск/ В. А, Алексеенко, М. В. Копанев, В. А. Целищев : ИрГУПС, 2017. – 38 с.
   
2. 
   ПрограммныйпакетElectronics Workbench 5.12portable, 1998.
   
3. 
   В.В. Сапожников, Ю.А. Кравцов, Вл.В. Сапожников. Теоретические основы железнодорожной автоматики и телемеханики : под ред. В.В. Сапожникова. – М.:УМЦ по образов. на ж.-д. трансп., 2008.- 393 с.