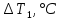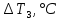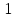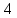Исследование нестационарной теплопроводности в диэлектрической среде
 Скачать 206.03 Kb. Скачать 206.03 Kb.
|
|
Санкт-Петербургский государственный электротехнический университет “ЛЭТИ” Кафедра физики ОТЧЕТ По Лабораторной работе №6 на тему: «Исследование нестационарной теплопроводности в диэлектрической среде» Выполнил: Фомичев Константин Вячеславович Факультет ФЭЛ Группа № 3282 Преподаватель: Черненко Юлия Сергеевна
Выполнено “____” ___________ Подпись преподавателя __________ Цель работы. Изучение закономерностей процесса тепловой диффузии и определение значения коэффициента тепловой диффузии исследуемого материала. Приборы и принадлежности. Установка для измерения температурного поля, создаваемого в среде тепловым источником. Исследуемые закономерности. Уравнение теплопроводности. Теплопроводность характеризует диффузию тепла в среде. Перенос энергии теплового движения в газах осуществляется через столкновения молекул, в твердых телах посредством передачи энергии колебаний кристаллической решетки. В обоих случаях процесс переноса теплоты описывается уравнением диффузии Фика: 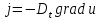 , ,где j - плотность теплового потока; u - объемная плотность внутренней энергии среды; 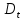 - коэффициент тепловой диффузии. Учитывая, что объемная плотность внутренней энергии связана с температурой среды соотношением - коэффициент тепловой диффузии. Учитывая, что объемная плотность внутренней энергии связана с температурой среды соотношением 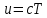 , где c - теплоемкость единицы объема среды, можно записать уравнение теплопроводности Фурье: , где c - теплоемкость единицы объема среды, можно записать уравнение теплопроводности Фурье:  , ,где 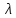 - коэффициент теплопроводности, - коэффициент теплопроводности,  . .Температурное поле точечного источника тепла. Рассмотрим задачу определения температурного поля T(x; t) в однородной среде. Положим, что температурное поле создается импульсным точечным источником тепла. Рассмотрим распространение тепла вдоль однородного бесконечного стержня, расположенного вдоль оси x. Начало координат совместим с положением нагревателя, который расположен перпендикулярно оси. Пусть в тонком поперечном слое при x = 0 и t = 0 мгновенно выделилось количество теплоты  . Выделившееся тепло диффундирует вдоль оси x. . Выделившееся тепло диффундирует вдоль оси x.Распределение тепла вдоль стержня в любой момент времени соответствует нормальному закону Гаусса: 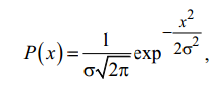 где Р (x) - вероятность того, что к некоторому моменту времени порция теплоты будет иметь координату x;  - среднеквадратичная ширина распределения. - среднеквадратичная ширина распределения. Тогда распределение линейной плотности тепла вдоль стержня равно: 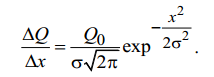 Разделим обе части этого равенства на произведение (сS), где с - теплоемкость единицы объема стержня, S - площадь его поперечного сечения: 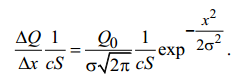 Левая часть данного выражения есть приращение температуры относительно исходной. Она равна приращению температуры  (x; t) в точке (x; t) в точке с координатой x в момент времени t по отношению к температуре в момент времени t = 0: Тогда искомое распределение температуры вдоль стержня имеет вид:  где T(0; t) - температура стержня к моменту времени t в точке среды с координатой x = 0;  - среднеквадратичная ширина распределения температуры по координате x. Кривые распределения температуры по координате для двух моментов времени показаны на рис. 11.1. - среднеквадратичная ширина распределения температуры по координате x. Кривые распределения температуры по координате для двух моментов времени показаны на рис. 11.1. 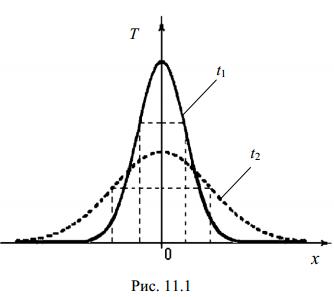 С увеличением времени параметр  увеличивается, при этом температура T(0; t), соответствующая максимуму распределения, уменьшается. увеличивается, при этом температура T(0; t), соответствующая максимуму распределения, уменьшается.Неравновесное состояние неравномерно нагретого стержня релаксирует к равновесному состоянию с одинаковой температурой во всех точках стержня. Зависимость  от времени можно представить в следующем виде: от времени можно представить в следующем виде:Формула (2) аналогична соотношению Смолуховского – Эйнштейна для среднеквадратичного смещения частицы, совершающей броуновские блуждания. Задача работы – сверить выводы теории теплопроводности в диэлектриках с экспериментом и определить значение коэффициента тепловой диффузии для исследуемого материала. Для этой цели зависимость (1), используя операцию логарифмирования, можно линеаризовать и привести к виду 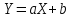 , где , где 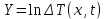 . .Коэффициенты a и b в этой линейной зависимости могут быть найдены методом наименьших квадратов (МНК). Для проверки закона 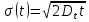 запишем его в виде запишем его в виде 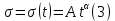 , ,где  . . Эту формулу также можно линеаризовать, используя операцию логарифмирования. В результате придем к зависимости где коэффициенты  и и  в которой также могут быть найдены по МНК. в которой также могут быть найдены по МНК.По найденному значению коэффициента 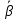 можно найти значение коэффициента можно найти значение коэффициента  , а затем значение коэффициента тепловой диффузии, , а затем значение коэффициента тепловой диффузии,Если полученное значение  близко к 1/2, то закон близко к 1/2, то закон 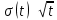 в данном опыте выполняется. Степень отличия в данном опыте выполняется. Степень отличия  от 1/2 может служить мерой невыполнения теоретических допущений в данном эксперименте. от 1/2 может служить мерой невыполнения теоретических допущений в данном эксперименте.Метод измерений. В работе исследуется нестационарное распределение температуры в среде после кратковременного нагревания среды в некотором малом объеме. Экспериментальная установка содержит электронагревательный элемент, имеющий форму пластины, и термометры, находящиеся на различных расстояниях от нагревателя. Пространство между нагревателем и термометрами заполнено кварцевым песком. Удельная теплоемкость песка  . .Геометрические размеры установки подобраны таким образом, что температурное поле вблизи нагревателя можно считать изменяющимся только вдоль одной координаты x. Направление оси x перпендикулярно плоскости пластины. Обработка результатов эксперимента. Вычислим приращение температуры среды относительно начальной температуры: 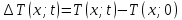 для каждого Т в точке x. для каждого Т в точке x.
Построим графики распределения приращения температур для каждого значения времени. 1.  : :  2. 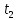 : :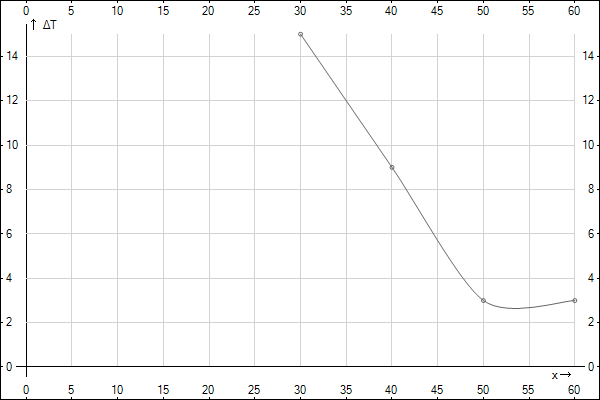 3.  : : 4.  : :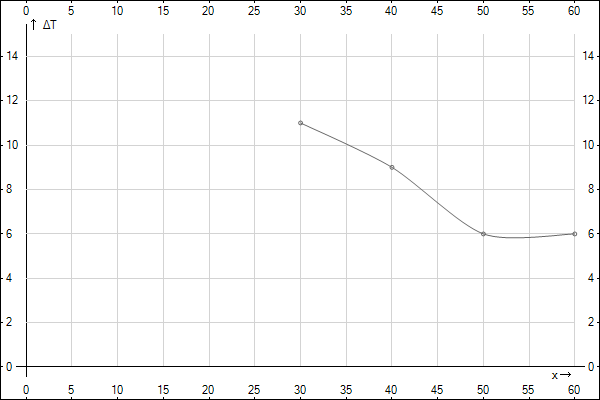 5.  : : 6. 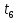 : :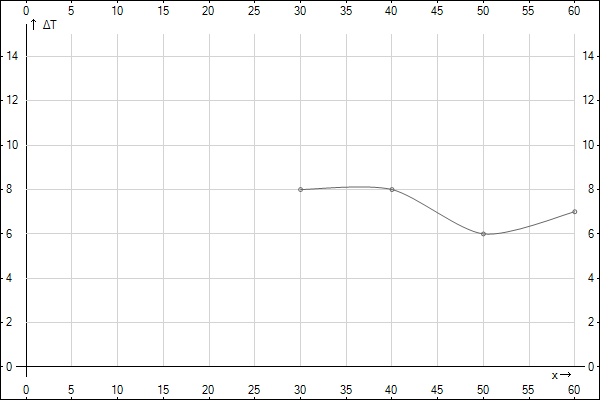 Введем обозначения  и и  . .Найдем коэффициенты  , , … линейных зависимостей … линейных зависимостей  , , ,… прологарифмированного уравнения (1) для каждого момента времени. ,… прологарифмированного уравнения (1) для каждого момента времени.     . .
  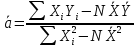
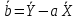
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||