ИО Теория. Исследование операций
 Скачать 117.51 Kb.
|
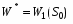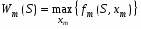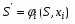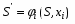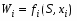     1.Определения:Исследование операций – дисциплина, занимающаяся разработкой и применением математических и количественных методов для нахождения оптимальных решений во всех областях целенаправленной человеческой деятельности. Операция – всякое мероприятие или система действий, объединённые единым замыслом и направленные на достижение какой-то цели, существующее во времени, проходящее различные этапы (фазы) развития и завершающийся получением конечного результата, сопоставимого с исходной целью. Оперирующие стороны – отдельные лица и коллективы, объединённые организационным руководством и активно стремящиеся к достижению поставленной цели. Активные средства проведения операции – совокупность материальных, энергетических, денежных, трудовых и других ресурсов, а также организационных возможностей, используемых оперирующей стороной для обеспечения успешного хода операции и достижения её цели. Действующие факторы операции – объективные условия и обстоятельства, определяющие её особенности и непосредственно влияющие на её исход. Различают факторы:
Все они разделяются на:
Пример определённого неконтролируемого фактора – сила притяжения Земли, смена сезонов года (мы знаем эти факторы, но не можем на них повлиять, константы) или количество минут в часах. Пример контролируемого фактора – количество войск в армии (известно количество человек в армии и оперирующая сторона может поменять это количество, переменная). Пример неопределённого неконтролируемого фактора – температура днем через два месяца (случайная величина). Критерий эффективности операции (целевая функция) – показатель требуемого, или ожидаемого, или достигнутого соответствия между результатом предпринимаемых действий и целью операции. Важнейшая функция критерия – возможность сравнительной оценки различных стратегий до начала их реализации. целевая функция, стратегии ОС, Математическая модель – формальные соотношения, устанавливающие связь принятого критерия эффективности с действующими факторами операции. Она должна быть достаточно полной (т.е. учитывать все важные факторы), но достаточно простой и исключать второстепенные факторы (чтобы можно было установить обозримые зависимости). 2. Общая запись задачи ИО в детерминированном и недетерминированном случае, оптимизация в среднем. Оптимизация: Детерминированный случай:  Когда все факторы заданы заранее: условия(а) и решения(х). Недетерминированный случай: 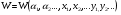 Добавляются неизвестные факторы (у). Задача поиска оптимального решения теряет определённость, т.к. нельзя максимизировать неизвестную величину. Это превращает её в задачу принятия решения в условиях неопределённости. Оптимизация в среднем:  Выше – функция распределения критериальной функции. Показатель эффективности – математическое ожидание. Можно решать максимизируя среднее значение критериальной функции. a – константы – определённые неконтролируемые факторы. x – переменные – неопределённые контролируемые факторы. y – случайные величины, а f(y…) – плотность вероятности т.е. неопределённые неконтролируемые факторы. Плотность вероятность - усреднённое значение критерия и максимизируем или минимизируем. Оптимизация в среднем- берётся значение фактора, попадающее в среднее значение. 3. Векторная операция, область согласия, область компромиссов. Уметь определить где область компромиссов по графику. Векторная операция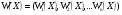 Вектор - набор частных скалярных критериев эффективности. 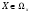 - область допустимых решений – когда допустимое множество всех возможных точек, которые удовлетворяют ограничениям задачи. - область согласия – когда возможно улучшение качества одновременно всех критериев или, по крайней мере, не ухудшение одного при увеличении другого. - область компромиссов – когда существуют противоречия между некоторыми критериями. В область согласия входят решения, для любого из которого можно найти решение из области компромиссов, превосходящее его по всем критериям. Нормализация вектора на основе введения вектора идеального качества операции Wи = (W1/Wи, W2/Wи …Wn/Wи) Или, в качестве идеального вектора принимается такой, компонентами которого являются максимумы локальных критериев. Проблемы векторной оптимизации:
4. Оптимальность по Парето. Оптима́льность по Паре́то — такое состояние некоторой системы, при котором значение каждого частного показателя, характеризующего систему, не может быть улучшено без ухудшения других. ... В экономике ситуация, когда достигнута эффективность по Парето, — это ситуация, когда все выгоды от обмена сторон исчерпаны. 5. Метод абсолютной и относительной справедливой уступки. Как свести к задаче оптимизации, как абсолютная справедливая уступка связана с экономической сверткой. Относительная уступка обеспечивает справедливый компромисс, если суммарный относительный уровень снижения качества по одному или нескольким критериям не превосходит суммарного относительного уровня повышения качества по остальным критериям. Лучшим по принципу абсолютной уступки считается компромисс, при котором абсолютное значение суммы снижения одного или нескольких критериев не превышает абсолютного значения суммы приращений оставшихся критериев. 6. Метод идеальной точки. Метод идеальной точки – в области допустимых значений неизвестных ищется такая их совокупность, которая способна обеспечить набор значений критериев, в том или ином смысле ближайших к наилучшему, но недосягаемому (точки утопии). Состоит в отыскании на границе Парето точки, ближайшей к точке утопии. На области определения заданы функции U и V, требуется решить задачу их максимизации. 7. Метод свертки Метод свёртывания – сведение многокритериальной задачи к задаче с одним критерием. 8. Метод уступок. Метод уступок – один или несколько критериев снижаются, в зависимости от совокупности других критериев (постепенно ослабляют первоначальные требования, невыполнимые совместно). Принцип равномерной уступки 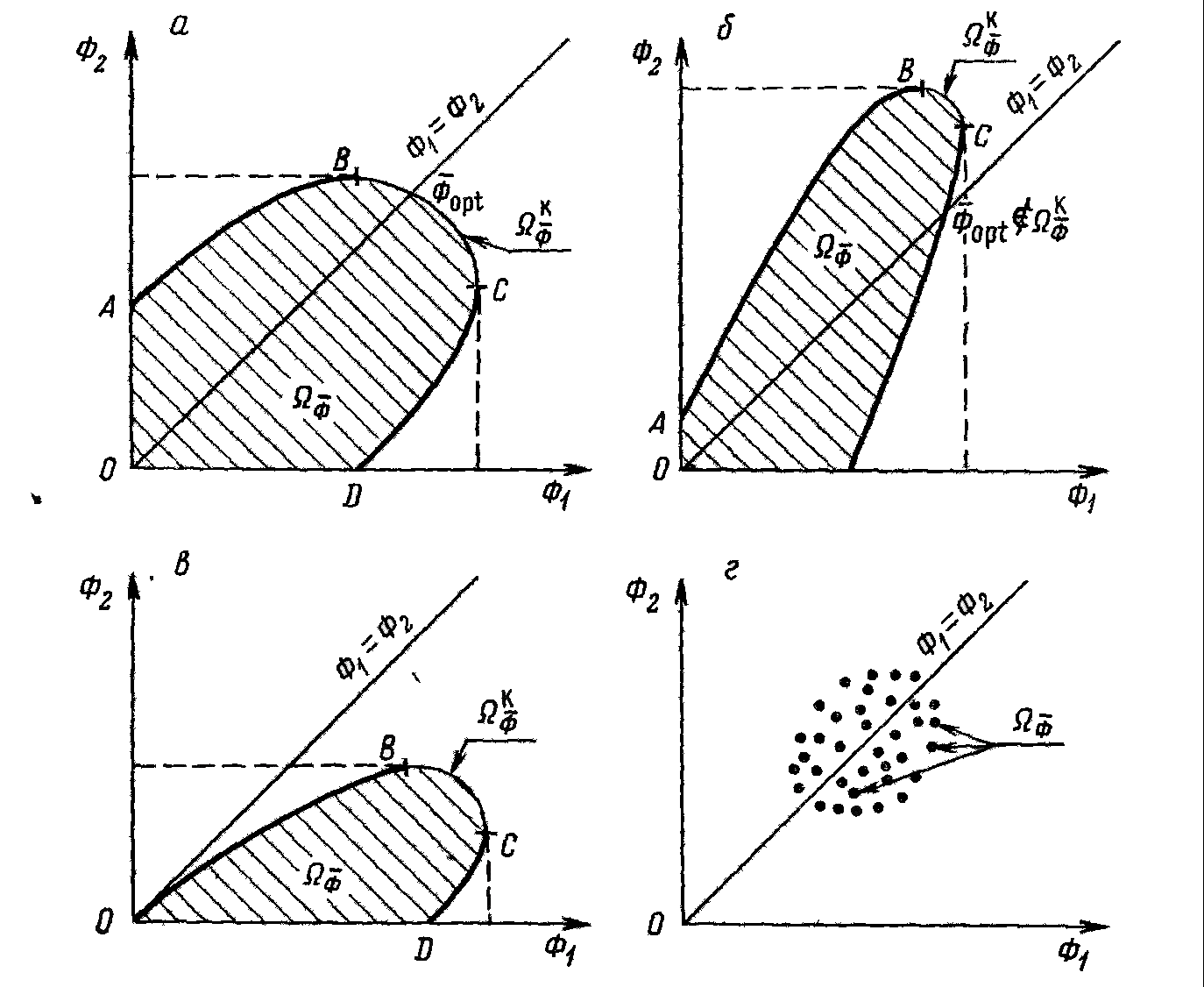 Недостаток – при равномерных уступках найденная оптима может просто не попасть в область компромиссов. Принцип максимина Выбирается наихудший из имеющихся критериев и по нему проводится максимизация. Суть в отыскании наибольшей точки, находящейся на границе Парето.  Принцип справедливой абсолютной уступки Справедливым считается такой компромисс, при котором суммарный абсолютный уровень снижения одного или нескольких критериев не превосходит суммарного абсолютного уровня повышения других критериев.  Принцип относительной справедливой уступки Справедливым является такой компромисс, при котором суммарный относительный уровень снижения одного или нескольких локальных критериев не превосходит суммарного относительного уровня повышения эффективности по остальным критериям. Важным преимуществом принципа является то, что он инвариантен к масштабу измерения критериев.  Принцип последовательных уступок Суть в последовательном сужении множества точек на границе Парето и выбора компромиссной пары критериев. Задача максимизации обоих критериев решения не имеет – точка утопии вне области допустимых решений.   9. Метод ограничений. Метод ограничений – множество допустимых значений неизвестных уменьшается путём осмысленного введения дополнительных ограничений. Задачи Динамического программирования. Примеры. Динамическое программирование (ДП) представляет собой математический метод, заслуга создания и развития которого принадлежит, прежде всего, Беллману. Метод можно использовать для решения весьма широкого круга задач, включая задачи распределения ре сурсов, замены и управления запасами, задачи о загрузке. Характерным для динамического программирования является подход к решению задачи по этапам, с каждым из которых ассо циирована одна управляемая переменная. Набор рекуррентных вычислительных процедур, связывающих различные этапы, обеспечивает получение допустимого оптимального реше ния задачи в целом при достижении последнего этапа. Фундаментальным принципом, положенным в основу теории ДП и лежащим в основе решения всех задач динамического программирования, является принцип оптимальности: «Каково бы ни было состояние системы S перед очередным шагом, надо выбрать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным». Динамическое программирование – это поэтапное планирование многошагового про цесса, при котором на каждом этапе оптимизируется только один шаг. Управление на каж дом шаге должно выбираться с учетом всех его последствий в будущем. При решении любой задачи динамического программирования удобно придерживаться раз и навсегда установленного, стандартного порядка действий. Этот порядок можно установить в следующей форме: 1. Выбрать способ описания процесса, т.е. параметры (фазовые координаты), характеризующие состояние S управляемой системы перед каждым шагом. 2. Разбить операцию на этапы (шаги). 3. Выяснить набор шаговых управлений xi для каждого шага и налагаемые на них ограничения. 4. Определить какой выигрыш приносит на i-ом шаге управление xi, если перед этим система была в состоянии S, т.е. записать «функцию выигрыша»: (3.2.1) Определить, как изменяется состояние системы S под влиянием управления xi на i-ом шаге: оно переходит в новое состояние: (3.2.2) 6. Записать основное функциональное уравнение динамического программирования, выражающее условный оптимальный выигрыш Wi(S) (начиная с i-го шага и до конца) через уже известную функцию Wi+1 (S): 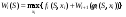 (3.2.3)Этому выигрышу соответствует условное оптимальное управление на i-м шаге xi (S) (причем в уже известную функцию Wi+1 (S): надо вместо S подставить измененное состояние ) Произвести условную оптимизацию последнего (m-го) шага, задаваясь гаммой состояний S, из которых можно за один шаг дойти до конечного состояния, вычисляя для каждого из них условный оптимальный выигрыш по формуле: (3.2.4) 8. Произвести условную оптимизацию (m-1)-го, (m-2)-го и т.д. шагов по формуле (3.2.3), полагая в ней i = (m-1),(m-2),…, и для каждого из шагов указать условное оптимальное управление Xi(S), при котором максимум достигается. Заметим, что если состояние системы в начальный момент известно (а это обычно бывает так), то необходимо найти оптимальный выигрыш по формуле: (3.2.5) 9. Далее найти безусловные оптимальные управления (и, если надо, конечное состояние 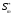 ) по цепочке: (3.2.6)В дальнейшем при решении задач распределения ресурсов будем придерживаться вышеизложенной схемы: условные оптимальные управления находятся в обратном порядке, от последнего шага к первому, а безусловные – в прямом порядке, от первого шага к последнему. Функция Белмана в общем виде. 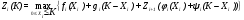 Условная и безусловная оптимизация для задачи о распределения ресурсов (1 ресурс), объяснить как решается. безусловной оптимизации — на искомое решение не налагается никаких дополнительных условий, кроме того, что оно должно доставлять минимум некоторой функции (другими словами, минимум функции ищется на всем пространстве — области определения функции). Мультипликативная задача динамического программирования, сведение к аддитивной. |