32 лаба ТОЭ. Исследование пассивных цепей при гармоническом воздействии на постоянной частоте
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
|
Министерство цифрового развития и массовых коммуникаций Российской Федерации Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технический университет связи и информатики» (МТУСИ) Кафедра Теории электрических цепей Отчет по лабораторной работе №32 по дисциплине «Электротехника» на тему: «Исследование пассивных цепей при гармоническом воздействии на постоянной частоте» Выполнил: студент группы БИН2206 Васильев Пётр Алексеевич Проверила: Степанова Анастасия Георгиевна Москва 2023 г. Содержание Цель работы С помощью программы Micro-Cap исследовать электрический режим конденсатора и катушки индуктивности в цепях гармонического тока. Сравнить полученные характеристики с помощью программы Micro-Cap, с аналогичными характеристиками, полученными расчётным путём. Задание на лабораторную работу Рассчитать в алгебраической форме комплексное сопротивление конденсатора Zc, определить его полное сопротивление |Zc| и аргумент arg(Zc) на пяти частотах 1, 2, 3, 4 и 5 кГц, если С=38,7. Построить векторную диаграмму. Полученные величины занести в таблицу 1 предварительного расчета. Рассчитать в алгебраической форме комплексное сопротивление ZRC RC-цепи для пяти частот 1, 2, 3, 4 и 5 кГц, определить его полное сопротивление и аргумент, если R=3 кОм, С=38,7 нФ. Построить векторную диаграмму. Полученные величины занести в таблицу 2 предварительного расчёта. Рассчитать напряжения на конденсаторе U2=U2eiꝕ, если U1=0,707e10 на частотах 1, 2, 3, 4 и 5 кГц, определить его модуль и фазу. Записать комплексное напряжение U2 в экспоненциальной форме. Полученные данные занести в таблицу 3 предварительного расчёта. Рассчитать в экспоненциальной форме комплексное сопротивление катушки индуктивности Z1 для пяти частот 1, 2, 3, 4 и 5 кГц, определить ее полное сопротивление и аргумент, если L=31 мГн. Построить векторную диаграмму. Полученные величины занести в таблицу 4 предварительного расчёта. Рассчитать в алгебраической форме комплексное сопротивление ZRL RL-цепи для пяти частот 1, 2, 3, 4 и 5 кГц, определить его полное сопротивление и аргумент, если R=3 кОм, L=31 мГн. Построить векторную диаграмму. Полученные величины занести в таблицу 5 предварительного расчёта. Рассчитать напряжение на катушке индуктивности U2=U2eiꝕ, если U1=0,707e10 для пяти частот 1, 2, 3, 4 и 5 кГц, определить его модуль и фазу. Записать комплексное напряжение U2 в экспоненциальной форме. Полученные данные занести в таблицу 6 предварительного расчёта. Расчетные формулы: Закон Ома для комплексных величин I=U/Z - комплексный ток U=Z*I – комплексное падение напряжения UL=j*ω*L*I=|UL|e j90ᵒ - комплексное напряжение на катушке UC=-j/(ω*C)*I=|UC|e -j90ᵒ - комплексное напряжение на конденсаторе Z=Re(Z)+jIm(Z)=R+jX=(R2+X2)1/2 *ejφ=Z*ejφ R=Re(Z) – резистивное сопротивление двухполюсника X=Im(Z) – реактивное сопротивление двухполюсника |Z|=Z – модуль комплексного сопротивления двухполюсника φ =arg(Z) – аргумент (фаза) комплексного сопротивления двухполюсника ω=2πf – угловая частота f – частота j=√(-1) – мнимая единица Для C-цепи ZC=-j*XC=-j/ (ω*C) = 1/(ω*C)*e-j90ᵒ=UC/I=|UC|/|I|*ej*arg(Uc/I) XC=1/ ω*C – ёмкостное сопротивление конденсатора Для L-цепи ZL=-j*XL=j*ω*L= ω*L*e j90ᵒ=UL/I=|UL|/|I|*ej*arg(Uc/I) XL= ω*L – индуктивное сопротивление катушки Ход выполнения лабораторной работы Сборка схемы с источником синусоидального напряжения и конденсатором 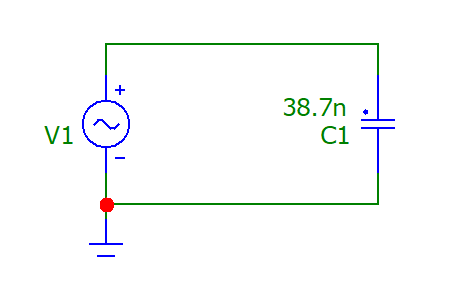 Рисунок 1 - Схема с источником синусоидального напряжения и конденсатором Таблица 1 - Результаты предварительного расчета
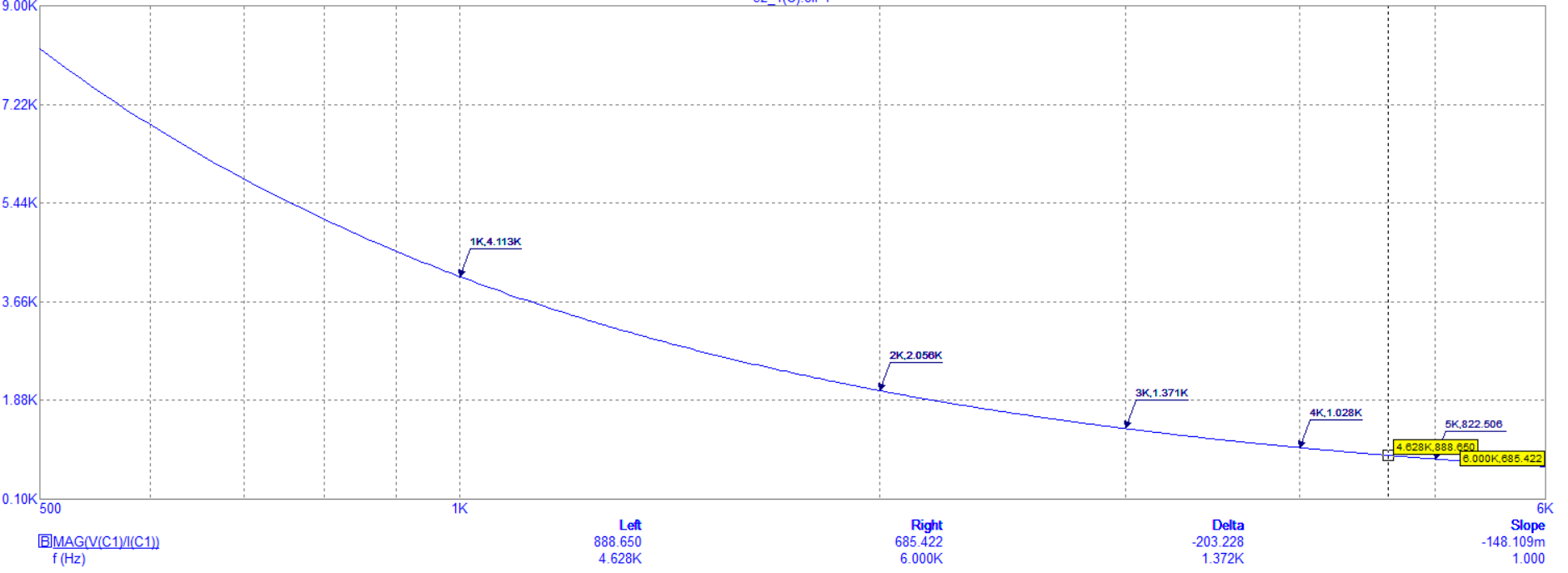 Рисунок 2 - График зависимости модуля сопротивления C-цепи от частот Вывод: Значение модуля сопротивления цепи уменьшается при увеличении частоты 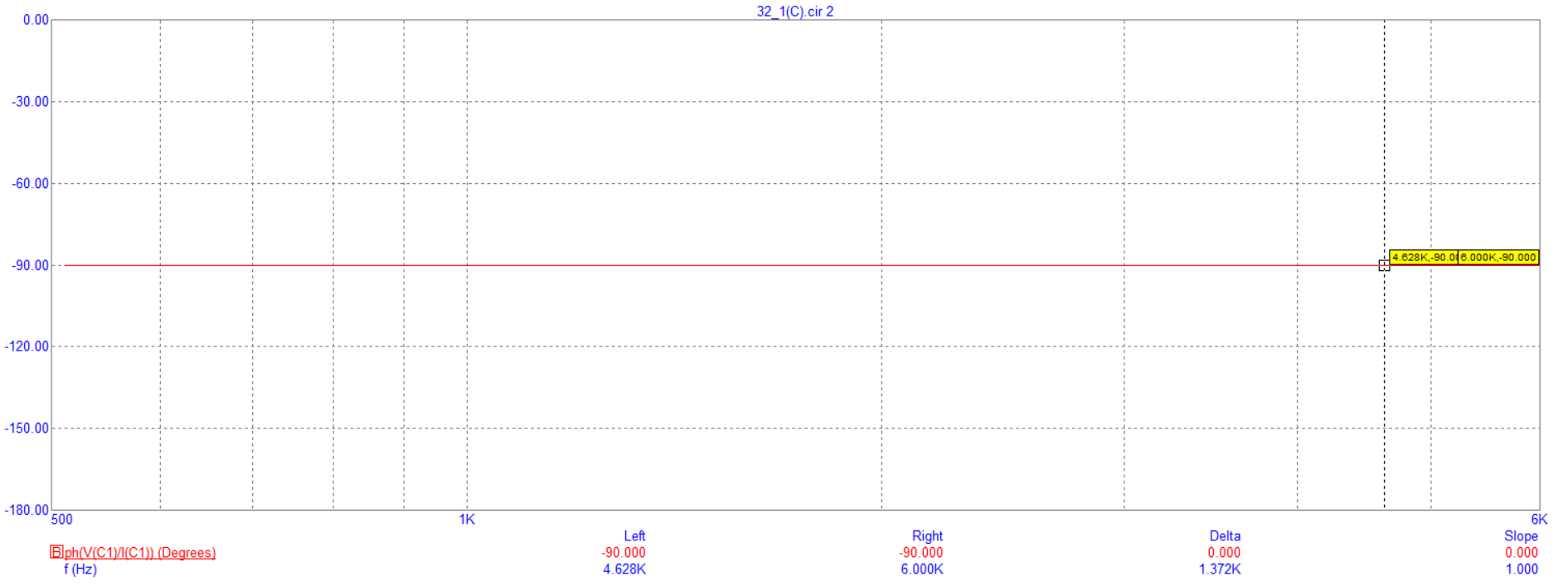 Рисунок 3 - График зависимости фазы сопротивления C-цепи от частоты Вывод: Падение напряжения увеличивается при увеличении сопротивления нагрузки. 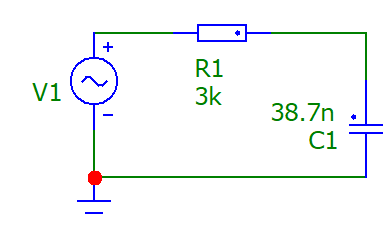 Рисунок 4 -RC-цепь Таблица 1
Таблица 2
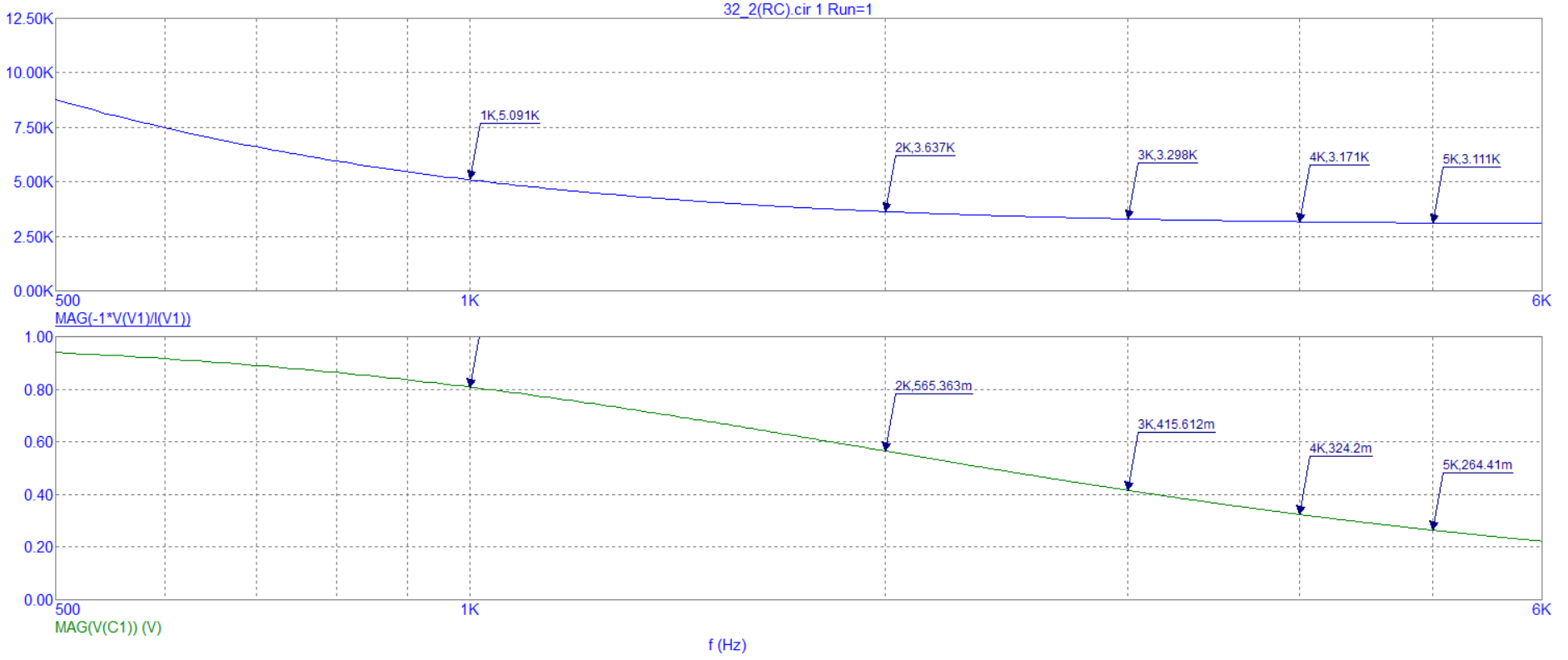 Рисунок 5- График зависимости модуля и фазы комплексного сопротивления RC-цепи от частоты Вывод: При увеличении частоты значение модуля комплексного сопротивления уменьшается, а его фаза растет. 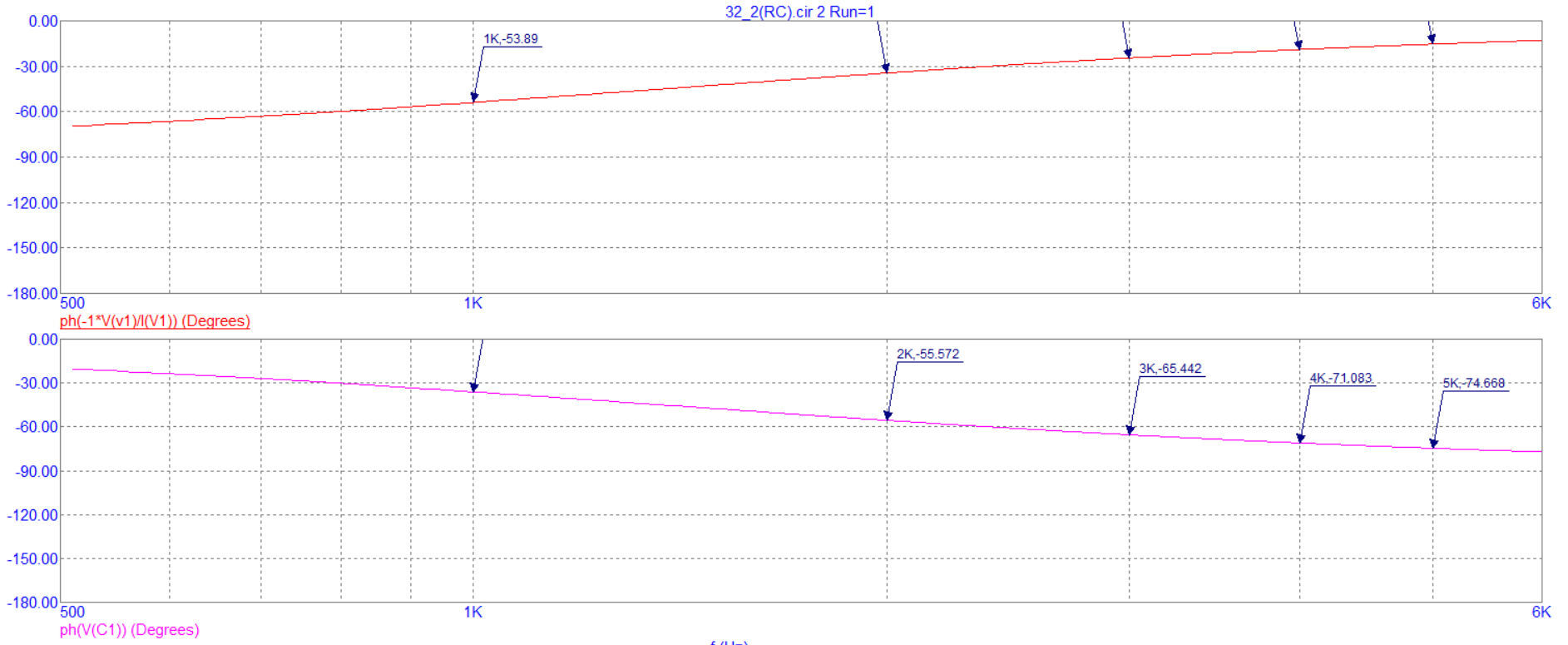 Рисунок 6 - График зависимости модуля и фазы комплексного напряжения нa конденсаторе RC-цепи от частоты Вывод: Значение модуля и фазы комплексного напряжения уменьшается при увеличении частоты. 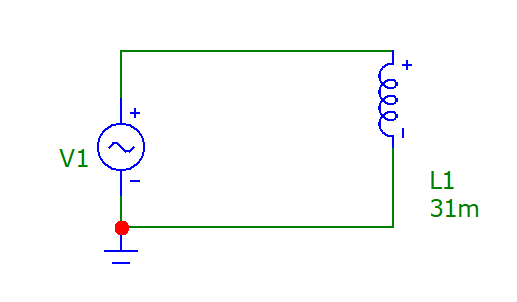 Рисунок 10 – Схема L-цепи Таблица 3
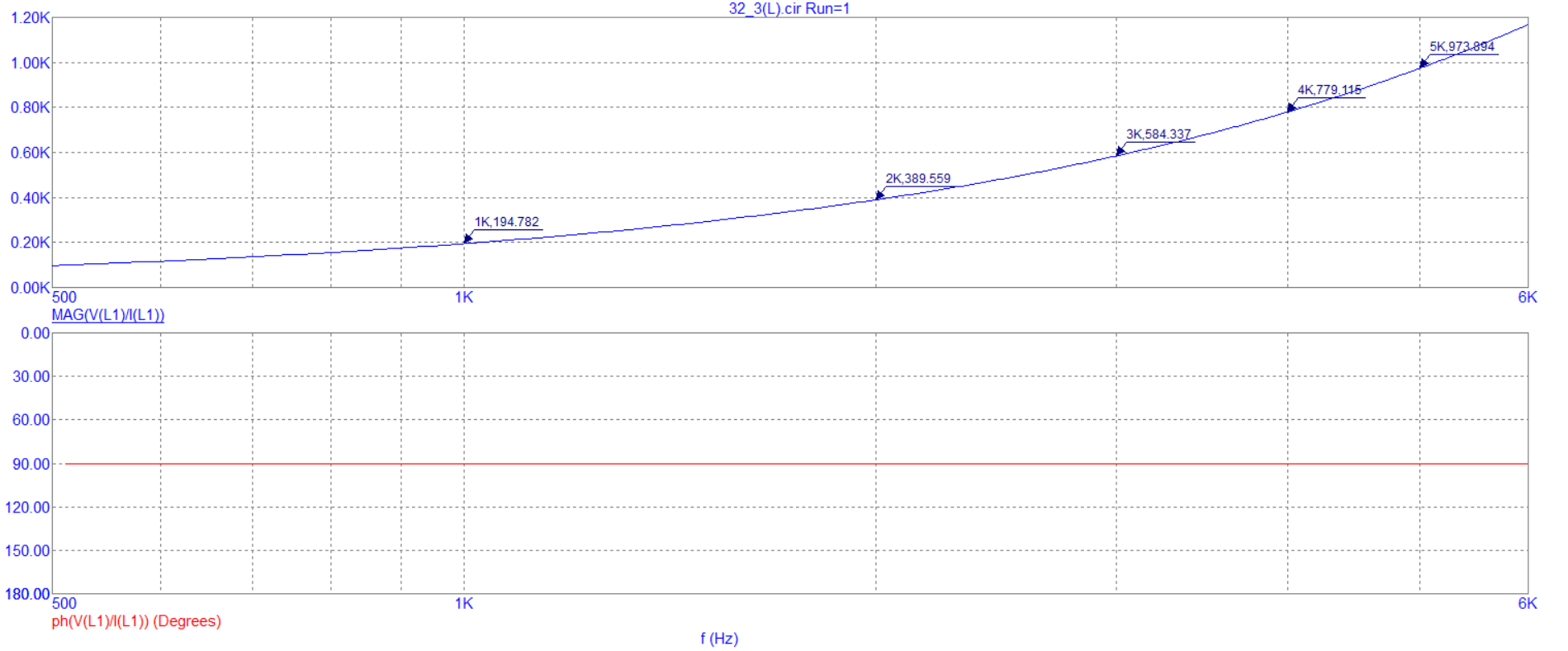 Рисунок 7 - График зависимости модуля и фазы комплексного сопротивления катушки L-цепи от частоты Вывод: Значение модуля комплексного сопротивления увеличивается, а его фаза не изменяется при увеличении частоты. 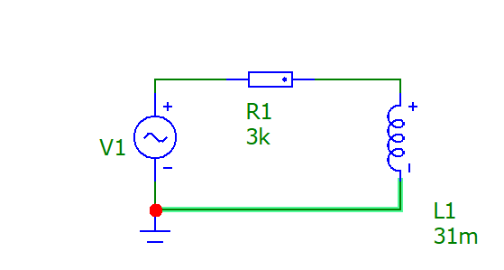 Рисунок 8 – схема RL-цепи Таблица 4
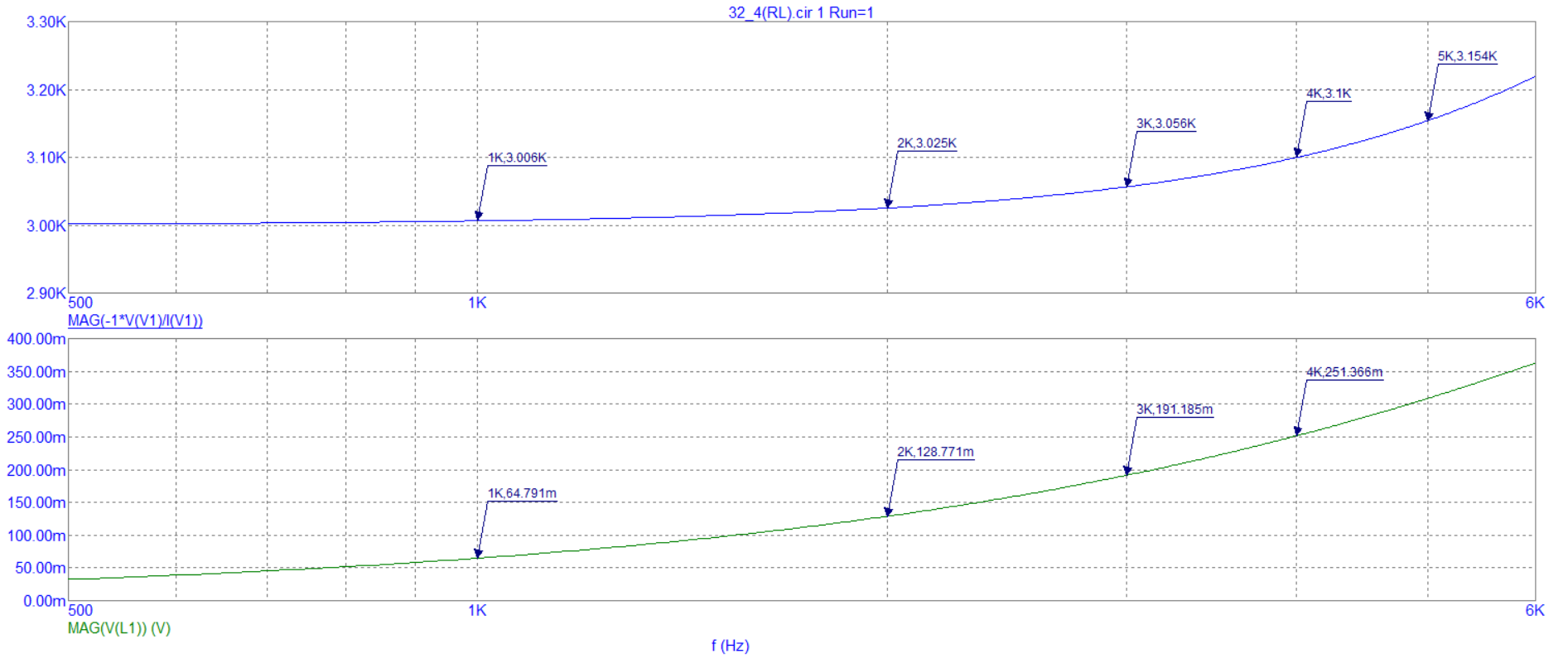 Рисунок 9 - График зависимости модуля и фазы комплексного сопротивления RL-цепи от частоты Вывод: Чем больше частота, тем больше увеличивается фаза. И с уменьшением частоты емкостное сопротивление катушки уменьшается. Таблица 5
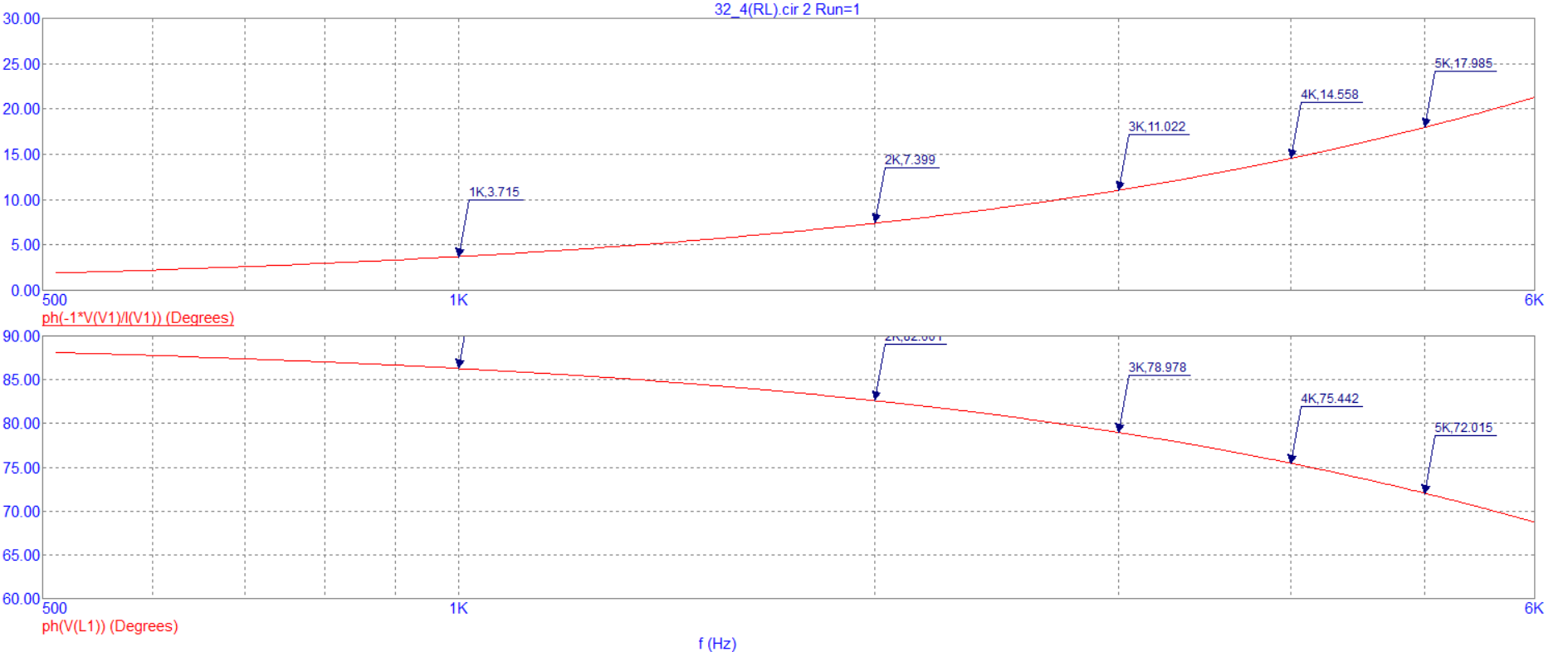 Рисунок 10 - График зависимости модуля и фазы комплексного напряжения на катушке RL-цепи от частоты Вывод: Значение модуля комплексного напряжения увеличивается, а его фаза уменьшается при увеличении частоты. Вопросы для самопроверки Какая частота называется граничной для RL – цепи? Ответ: Частота, на которой действительная и мнимая часть комплексного входного сопротивления равны, называется граничной. Каково значение модуля входного сопротивления RL – цепи на граничной частоте? Ответ: |Zвх|=R√2 Каково значение аргумента входного сопротивления RL – цепи на граничной частоте? Ответ: arg(Z)=44.98o К чему стремится модуль тока RL – цепи при увеличении частоты? Ответ: 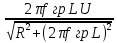 =U =U С ростом частоты входное сопротивление цепи RL возрастает, а модуль тока уменьшается. И стремится к нулю. Чему равен модуль входного сопротивления RL – цепи при частоте равной нулю? Ответ: Модуль входного сопротивления RL-цепи при частоте равной нулю равен сопротивлению на резисторах | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
