Исследование трёхфазных цепей при соединении фаз потребителя треугольником цель работы
 Скачать 428.05 Kb. Скачать 428.05 Kb.
|
|
Лабораторная работа 4 ИССЛЕДОВАНИЕ ТРЁХФАЗНЫХ ЦЕПЕЙ ПРИ СОЕДИНЕНИИ ФАЗ ПОТРЕБИТЕЛЯ ТРЕУГОЛЬНИКОМ Цель работы Экспериментально установить влияние характера, несимметрии нагрузки и неполнофазного режима работы, на токи и напряжения исследуемой цепи. Определить соотношения между фазными, линейными токами и напряжениями при различных режимах работы потребителя. Общие сведения Соединить фазы потребителя треугольником – это последовательно соединить все его фазы, образовав треугольник a-b-с, к началам фаз потребителя а, b, с подается напряжение от источника питания (рис. 4.1). 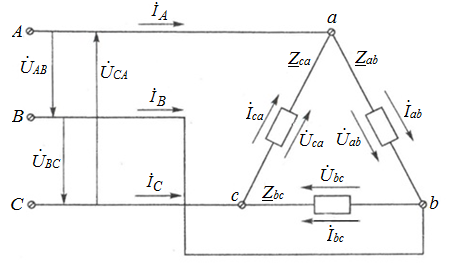 Рис. 4.1. Схема соединения фаз потребителя треугольником На рис. 4.1: 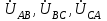 – линейное напряжение источника (UЛ); – линейное напряжение источника (UЛ);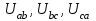 – фазные напряжения нагрузки (UФ); – фазные напряжения нагрузки (UФ);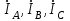 – линейные токи (IЛ); – линейные токи (IЛ);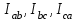 – фазные токи нагрузки (IФ); – фазные токи нагрузки (IФ);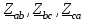 – полные комплексные сопротивления фаз нагрузки. – полные комплексные сопротивления фаз нагрузки.Если пренебречь потерями напряжения в соединительных проводах, то фазные напряжения нагрузки равны, соответствующимлинейнымнапряжениямсети, т. е. 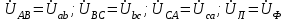 . (4.1) . (4.1)Расчеты в 3-фазной электрической цепи при соединении нагрузки треугольником осуществляются по следующим формулам: напряжения нагрузки на комплексной плоскости 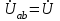 ; ;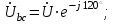 (4.2) (4.2)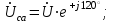 комплексы фазных действующих токов потребителя вычисляются согласно закону Ома по формулам: 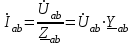 ; ;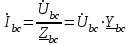 ; (4.3) ; (4.3)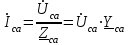 , ,где 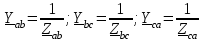 –комплексы проводимостей фазных нагрузок; –комплексы проводимостей фазных нагрузок;линейные токи сети вычисляются на основании первого закона Кирхгофа для узлов а, b и с цепи потребителя 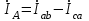 ; ;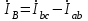 ; (4.4) ; (4.4)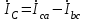 ; ;комплексная полная мощность для каждой фазы потребителя 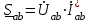 ; ;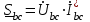 ; (4.5) ; (4.5)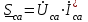 . .полная мощность 3-фазной цепи 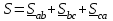 . .При симметричной нагрузке в фазах потребителя 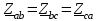 ; фазные токи ; фазные токи 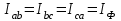 ; линейные токи ; линейные токи 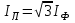 ; полная мощность трехфазной цепи ; полная мощность трехфазной цепи 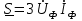 . .Таблица 4.1 Значение токов и напряжений исследуемой цепи
По результатам замеров построить векторные диаграммы напряжений и токов. Для опыта 2.1. – «Нагрузка, симметричная во всех фазах», сделать следующий расчет: напряжения источника (потребителя) 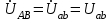 ; ;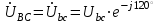 ; ;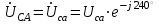 ; ;фазные токи потребителя: 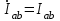 ; ;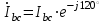 ; ;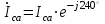 ; ;линейные токи потребителя: 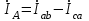 ; ;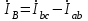 ; ;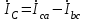 ; ;– найти соотношение действующих значений линейных и фазных токов: 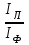 ; ;– сумма фазных токов: 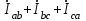 ; ;– сумма линейных токов: 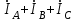 . .По результатам расчета для опыта 2.1 построить векторные диаграммы напряжений и токов в одной системе координат. Для опытов 2.2 и 2.3 расчет не производится, диаграммы строятся аналогично опыту 2.1. Порядок построения векторных диаграмм напряжений и токов сактивной нагрузкой По результатам измерений опытов 2.1; 2.2; 2.3 – осуществляется построение диаграмм напряжений и токов в следующей последовательности: строятся векторы напряжений в выбранном масштабе напряжений 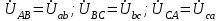 ; ;2) строятся векторы токов 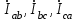 , так как нагрузка в фазах активная, ток и напряжение совпадают по фазе, начала векторов тока и напряжения находятся в одной точке; , так как нагрузка в фазах активная, ток и напряжение совпадают по фазе, начала векторов тока и напряжения находятся в одной точке;3) строятся векторы линейных токов путем векторного сложения (масштаб тот же, что и для фазных токов), (рис. 4.3, 4.4): 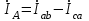 ; ;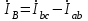 ; ;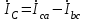 . .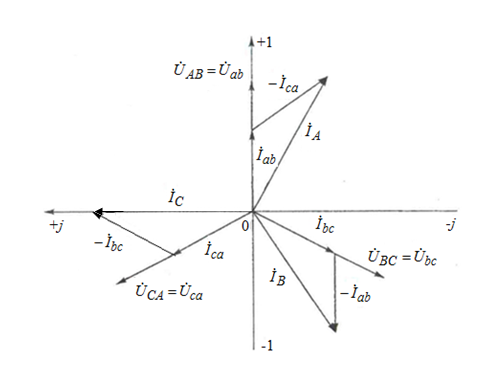 Рис. 4.3. Векторная диаграмма напряжения и токов с симметричной активной нагрузкой в фазах потребителя 2. По результатам измерений опыта 2.4. – «Обрыв фазы потребителя» – осуществляется построение диаграммы напряжений и токов в следующей последовательности: 1) строятся векторы напряжений 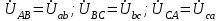 ; ;2) строятся векторы токов 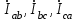 ; ;3) путем векторного сложения, согласно системе уравнений, строятся линейные токи 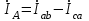 ; ;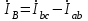 ; ;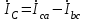 ; ;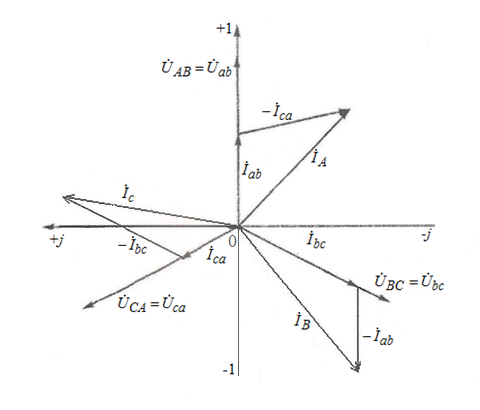 Рис. 4.4. Векторная диаграмма напряжения и токов при несимметричной нагрузке в фазах потребителя 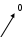 Пример. Обрыв фазы аb (рис. 4.5), Пример. Обрыв фазы аb (рис. 4.5), 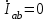 , система уравнений (4.4) приобретает следующий вид: , система уравнений (4.4) приобретает следующий вид: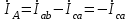 ; ; 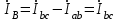 ; ;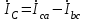 . .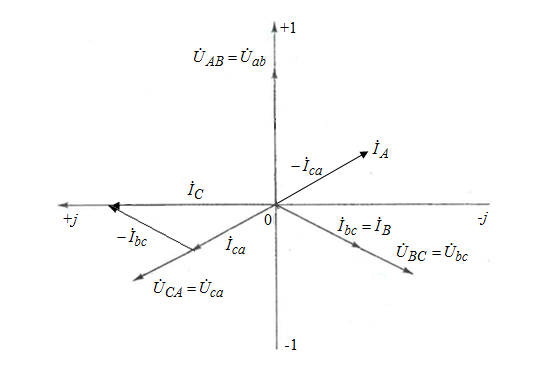 Рис. 4.5. Векторная диаграмма напряжений и токов при обрыве фазы ab 3. По результатам измерений опыта 2.5 – «Обрыв линейного провода» – строится диаграмма напряжений и токов с учетом изменений, произошедших на схеме. Схема, полученная после обрыва, должна быть представлена в отчете. Пример. Оборван линейный провод А-а, полученная схема (рис. 4.6) 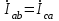 – один и тот же ток, протекающий через резисторы Rab и Rca; – один и тот же ток, протекающий через резисторы Rab и Rca;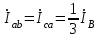 ; ;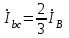 . .Вместо 3-фазной цепи при соединении фаз потребителя в треугольник получилась разветвленная однофазная цепь с последовательно-параллельным соединением трех резисторов, причем Rab = Rbc = Rca. 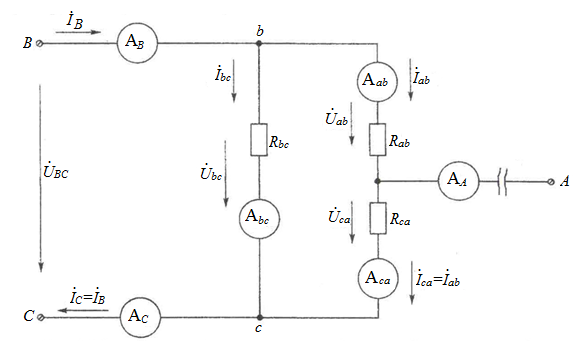 Рис. 4.6. Разветвленная цепь нагрузки при обрыве линейного провода А–а Согласно схемы, напряжения потребителя 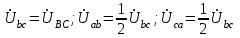 . (4.6) . (4.6)Порядок построения диаграммы при обрыве линейного провода А–а: строится напряжение источника 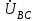 (расположение вектора как в 3-фазной цепи, до обрыва); (расположение вектора как в 3-фазной цепи, до обрыва);строятся напряжения и токи, полученные в результате измерений в опыте 2.5, так как нагрузка носит активный характер, следовательно, в однофазной цепи все напряжения и токи совпадают по фазе (все векторы накладываются друг на друга), рис. 4.7. 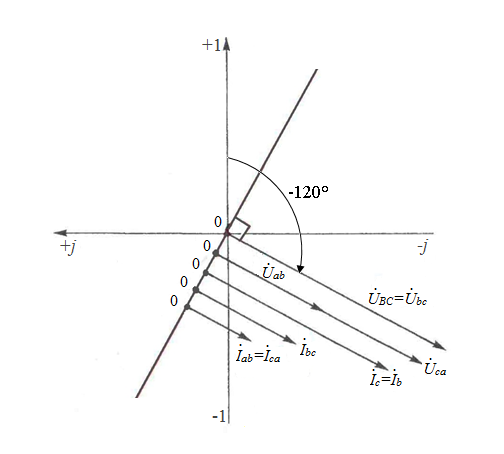 Рис. 4.7. Векторная диаграмма напряжений и токов при обрыве линейного провода А–а 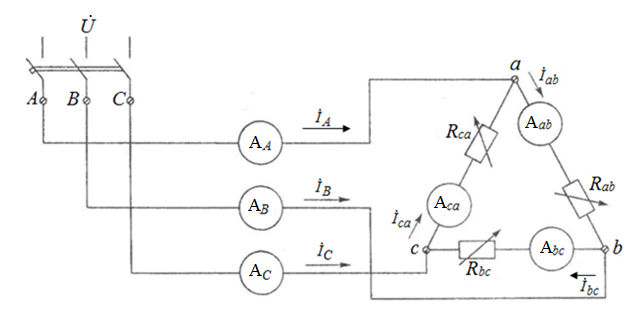 Рис. 4.8. Схема опыта по исследованию трехфазной цепи при соединении фаз потребителя треугольником  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
