Ряды. Исследовать сходимость числовых рядов с помощью интегрального пр. Исследовать сходимость числовых рядов с помощью интегрального признака
 Скачать 70.5 Kb. Скачать 70.5 Kb.
|
|
Исследовать сходимость числовых рядов с помощью интегрального признака  Найти 3 первых отличных от нуля члена разложения в степенной ряд решений дифференциального уравнения: При данных начальных условиях решение уравнения будем искать в виде разложения в ряд Маклорена. Осталось только определить коэффициенты ряда. Первые два коэффициента уже известны – это начальные условия. Для определения третьего коэффициента подставим начальные условия в исходное дифференциальное уравнение: 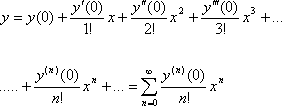 Таким образом, первые три члена разложения равны нулю. Придется много дифференцировать, чтобы найти отличные от нуля члены разложения. А т.к. уравнение нелинейное то другие способы решения (например, метод сравнения неопределенных коэффициентов) применять нельзя. Для нахождения следующих членов разложения дифференцируем по х обе части исходного дифференциального уравнения: Таким образом, найден первый ненулевой член разложения: Для нахождения следующего члена разложения опять дифференцируем только что полученное выражение по х. Находим значение в нуле и т.д. пока не получим еще два ненулевых члена разложения. 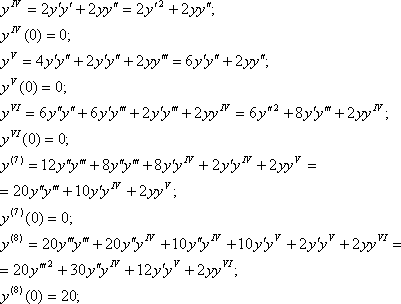 Нашли второй ненулевой член разложения: 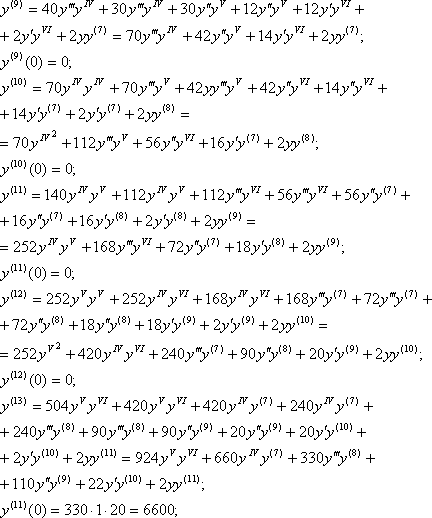 Теперь найден третий ненулевой член разложения: Получаем, что решение дифференциального уравнения имеет вид: Подставим полученный результат в исходное уравнение: 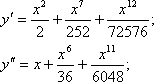 Как видно, при х достаточно близких к начальным условиям, последние три слагаемых практически равны нулю, и равенство выполняется. |
