Исследовательская работа по геометрии. Исследовательская работа по геометрии по теме Многоугольники. Сумма углов выпуклого многоугольника 8 класс. Цель Закрепление знаний при определении многоугольника. Вывод формулы суммы углов многоугольника

• Название: Исследовательская работа по геометрии по теме Многоугольники. Сумма углов выпуклого многоугольника 8 класс. Цель Закрепление знаний при определении многоугольника. Вывод формулы суммы углов многоугольника
• Анкор: Исследовательская работа по геометрии
• Дата: 17.09.2017
• Размер: 58 Kb.
• Имя файла: Исследовательская работа по геометрии.doc
• Тип: Исследовательская работа; #32991
• Категория: Математика

Свиридова Елена Сергеевна

Исследовательская работа по геометрии по теме «Многоугольники. Сумма углов выпуклого многоугольника» 8 класс.

Цель: Закрепление знаний при определении многоугольника. Вывод формулы суммы углов многоугольника.
Определение. Многоугольником называется фигура, составленная из отрезков таким образом, что смежные отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек.
1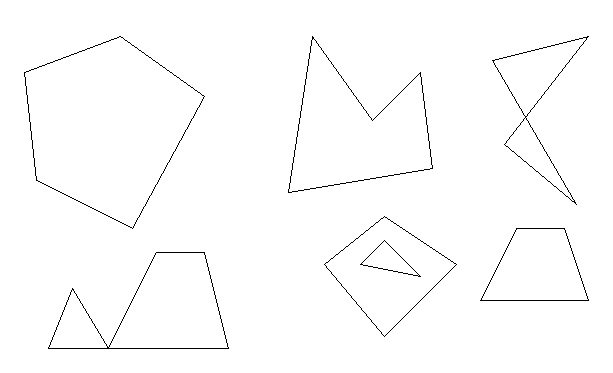. Обозначить фигуры. Пользуясь определением, исследовать фигуры и сделать вывод какие фигуры являются многоугольником, какие не являются. Данные занести в таблицу.

№ фигуры	Ход рассуждений	вывод

2. 
   Вывод формулы суммы углов выпуклого многоугольника.
   

Вывод формулы суммы углов выпуклого многоугольника вытекает из ранее полученных знаний о сумме углов произвольного треугольника.
1. Составить выпуклый многоугольник из 2- х треугольников.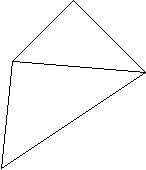



Так как сумма углов в треугольнике равна 180◦, то сумма

Углов в четырехугольнике равна 360◦ .


2. Составить выпуклый многоугольник из 3-х треугольников, 4-х и т.д.

2. 
   Занести данные в таблицу:
   

Фигура	Количество треугольников	Число сторон в многоугольнике	формула
четырехугольник	2	4	180(4-2)
Пятиугольник	3	5	180(5-2)
шестиугольник	4	6	180
семиугольник	5	7	180
n - угольник	n -2	n	180

Решить задачи:

1. 
   В выпуклом многоугольнике три угла по 80 градусов, а остальные - 150 градусов. Сколько углов в выпуклом многоугольнике?
   
2. 
   Какое количество вершин может иметь многоугольник, если величина каждого из углов менее 120 градусов?
   

Решение: -------------------------------------------------------------------------------------------------

Решение:

Для решения данной задачи воспользуемся теоремой о сумме углов выпуклого многоугольника.
Теорема гласит: Для выпуклого n-угольника сумма углов равна 180°(n-2).
Значит, для нашего случая:
180(n-2)=3*80+x*150, где
3 угла по 80 градусов нам даны по условию задачи, а количество остальных углов нам пока неизвестно, значит обозначим их количество как x.
Однако, из записи в левой части мы определили количество углов многоугольника как n, поскольку из них величины трех углов мы знаем по условию задачи, то очевидно, что x=n-3.
Таким образом уравнение будет выглядеть так:
180(n-2)=240+150(n-3)

Решаем полученное уравнение

180n - 360 = 240 + 150n - 450

180n - 150n = 240 + 360 - 450

30n = 150

n=5

Ответ: 5 вершин
2.Для решения данной задачи воспользуемся теоремой о сумме углов выпуклого многоугольника.
Теорема гласит: Для выпуклого n-угольника сумма всех углов равна 180°(n-2).
Значит, для нашего случая необходимо сначала оценить граничные условия задачи. То есть, сделать допущение, что каждый из углов равен 120 градусам. Получаем:
180(n-2)=120n

180n - 360 = 120n

180n - 120n = 360 (это выражение рассмотрим отдельно ниже)

60n = 360

n=6

Исходя из полученного уравнения, делаем вывод: при величине углов менее 120 градусов, количество углов многоугольника менее шести.
Объяснение:

Исходя из выражения 180n - 120n = 360 , при условии, что вычитаемое правой части будет менее 120n, разность должна быть более 60n. Таким образом, частное от деления всегда будет менее шести.
Ответ: количество вершин многоугольника будет менее шести.