|
|
КР. Истечение газа через суживающееся сопло и сопло Лаваля. Истечение газа через суживающееся сопло и сопло Лаваля. Скачки уплотнения
Истечение газа через суживающееся сопло и сопло Лаваля. Скачки уплотнения
Параметры истечения. Потенциальная энергия в кинетическую (схема 1) преобразуется в сопловых аппаратах, или просто соплах. В предыдущем параграфе указывалось, что для получения скоростей, меньших или равных критическим, применяют суживающиеся сопла, а для получения сверхкритических скоростей — сопла с суживающейся и расширяющейся частями, называемые соплами Лаваля (см. рис. 4.1, а).
Рассмотрим случай истечения упругой жидкости при постоянных начальных параметрах среды и при начальной скорости, близкой к нулю (№', =0).
Построим по (4.6) зависимость скорости потока от величин Р = р2/Р и (Зкр = рщУРх для сопла Лаваля (рис. 4.3, а).

Рис. 4.3. Зависимость скорости (а) и расхода (б) потока рабочего тела от отношения давлений
Как следует из рис. 4.3, а, скорость возрастает во всем диапазоне значений р. При Р = Ркр кривая скорости имеет перегиб.
На этом же графике приведена кривая скорости для суживающихся сопел (пунктирная линия). От Р = 1 до Р = Ркр кривые скорости для обоих сопел совпадают. При Р < Ркр кривая скорости для суживающихся сопел параллельна оси абсцисс с ординатой, равной критической скорости. В таких соплах нельзя получить скорости выше критических, поэтому в формулу (4.6) при Р < Ркр подставляют величину Ркр. Суживающиеся сопла при Р < Ркр применять нецелесообразно, поскольку перепад давлений (рис. 4.4) не может быть использован полностью.
Формула расчета величины критического отношения давлений выводится из соотношения
 
Рис. 4.4. Использование перепада давлений в суживающихся соплах
Используя соотношение параметров в адиабатном процессе (2.15), выразим критические параметры через начальные и (Зкр, подставим их в формулу расчета величины критического отношения давлений, освободимся от радикалов и получим
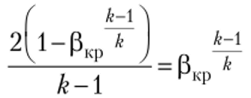
или

Критическое отношение давлений (Зкр = Ркр/Р зависит только от физических свойств газа (от его показателя адиабаты) и может быть вычислено.
Формула для получения критической скорости получается подстановкой значений ркр в (4.6):

где — постоянная величина, зависящая от показателя адиабаты (табл. 4.1).
При заданных начальных параметрах жидкости массовый расход М5 достигает максимальной величины М™ах при скорости истечения, равной критической, которая, как известно, имеет место в сечении Атт сопла (рис. 4.3, б). Поэтому при р > ркр расход определяется по (4.8), а когда Р < ркр - по формуле при р = ркр:

где а2 — постоянная величина, зависящая от показателя адиабаты & (табл. 4.1). Значения коэффициентов (3|ф, а{ и а2 приведены в табл. 4.1.
Таблица 4.1
Постоянные для вычисления критической скорости и максимального расхода газа
Рабочее тело
|
Показатель адиабаты к
|
Ркр
|
«1
|
сс2
|
Газ (двухатомный)
|
1,40
|
0,528
|
1,08
|
0,686
|
Перегретый пар
|
1,30
|
0,546
|
1,055
|
0,667
|
Сухой насыщенный пар (в пределах от 0 до 150°С)
|
1,135
|
0,577
|
1,03
|
0,623
|
Для сопла Лаваля массовый расход определяется в минимальном сечении при критической скорости по (4.14). Наиболее просто скорость истечения водяного пара находят по (4.5) с помощью ?5-диаграммы, приведенной на рис. 4.5. Проведя адиабату из точки 7, характеризующей начальное состояние рабочего тела до изобары р2, определяют начальное и конечное
значения энтальпии, а затем и скорость истечения по (4.5). Критическую скорость определяют по энтальпии при критическом давлении ркр = Ркр/^1 •

Рис. 4.5. Процесс расширения пара в сопле Лаваля на ?5-диаграмме:
/г, — адиабатный перепад энтальпий
Таким образом, сопло Лаваля способно обеспечить достижение сверхзвуковой скорости, используя весь перепад давления, но расход газа при этом не возрастает выше расхода при критической скорости.
Принципиальная схема струйного аппарата для пневмотранспорта
и изменение давления по его длине приведены на рис. 4.6. В соответствии с данной схемой рабочий воздух с давлением р{ подводится к соплу 1. Поскольку обычно (3 < (Зкр, то сопло имеет расширяющуюся часть (сопло Лаваля). В нем давление воздуха снижается до р2, а скорость возрастает до 1^2 > в выходном сечении сопла. Рабочий воздух, выходящий из сопла в приемную камеру 3 со скоростью инжектирует из приемного патрубка 2 сыпучий материал и передает ему часть кинетической энергии. Смесь воздуха и транспортируемого материала поступает в камеру смешивания 4У где ноле скоростей выравнивается и давление повышается до /?3. Далее смесь поступает в диффузор 5 — и давление потока в данном сечении повышается до рс.

Рис. 4.6. Принципиальная схема струйного аппарата для пневматического транспорта
Струйные аппараты рассчитываются на основании законов термодинамики, гидро- и газодинамики.
Геометрические размеры сопел струйных аппаратов определяют но формулам термодинамики.
При отношении давлений р2/Р < Р1ф рабочее сопло аппарата выполняется расширяющимся. Критическое сечение сопла Лт1п находят из уравнения сплошности:

В (4.15) величина М5 задана, Укр определяют из уравнения адиабаты:  а критическую скорость вычисляют по (4.13). а критическую скорость вычисляют по (4.13).
Выходное сечение сопла Лаваля также вычисляют по уравнению сплошности:

где 1У2 — скорость на выходе ив сопла, определяемая но (4.6).
Удельный объем находят из уравнения адиабаты:

Определив величины Ат[п и А2 и задавшись углом конусности 10—12°, можно найти длину расширяющейся части сопла.
Профиль и длину входной части сопла до критического сечения выбирают из конструктивных соображений.
Скачок уплотнения. Когда в потоке газа под влиянием какого-либо возмущения (обтекания препятствия и т.н.) происходит резкая, практически мгновенная перестройка течения, резкое торможение и сжатие сверхзвукового потока и переход его к дозвуковому, такую перестройку потока называют адиабатическим скачком уплотнения. Подобные скачки уплотнения весьма распространены в реальных сверхзвуковых течениях. После скачка уплотнения происходит возрастание статического давления, температуры и плотности газа, но резкое снижение полного давления (давление торможения) /?* и плотности торможения р*.
Если плоскость скачка уплотнения располагается перпендикулярно движению потока, то адиабатический скачок уплотнения называется прямым. В сверхзвуковых потоках, как показывает опыт, возникают и косые скачки, расположенные под углом к направлению потока. В косом скачке меняется не только величина, но и направление скорости движения.
При полете летательного аппарата со сверхзвуковой скоростью при входе воздуха в воздухозаборный канал имеют место значительные потери полного давления, связанные с образованием скачков уплотнения. Работоспособность воздуха в двигателе будет тем больше, чем меньше эти потери, поэтому организация входа воздуха, создание оптимальных скачков уплотнения имеют решающее значение для применения таких аппаратов.
Тепловой скачок. В тех случаях, когда на весьма малом участке канала происходит выделение теплоты, вызывающее мгновенную перестройку течения, то говорят о тепловых скачках. Для дозвуковой области течения выделение теплоты приводит к однозначному изменению состояния: расширению газа и увеличению скорости (числа Маха). Для сверхзвуковой области течения возникают сложные тепловые скачки.
Значительный интерес могут представлять два вида тепловых скачков: распространение детонации горения и так называемые скачки конденсации.
Детонационное горение. В отличие от медленного горения, детонационное горение распространяется с огромными скоростями (порядка нескольких километров в секунду) и сопровождается значительными разрушительными действиями. Последнее свидетельствует о возникновении в самой волне (и особенно при обтекании ею препятствий) весьма высоких давлений. Известно, что скорость распространения детонационной волны превосходит скорость звука в начальной смеси.
По мнению Л. А. Вулиса, детонационная волна представляет собой два последовательных скачка: адиабатический, переводящий газ из сверхзвукового движения в дозвуковое, и тепловой — в дозвуковом потоке. Схема детонационной волны представлена на рис. 4.7. Так, на участке 1—2 происходит адиабатический скачок уплотнения, а в зоне горения 2—3 — тепловой скачок во фронте пламени. (Более подробные сведения можно почерпнуть из специальной литературы.)

Рис. 4.7. Схема детонационной волны во фронте пламени
Для сравнения работы сопла Лаваля при расчетном и нерасчетных режимах работы рассмотрим реакцию струи, когда из ракетного двигателя (рис. 4.8) происходит истечение жидкости или газа со скоростью XVа.
При сверхкритическом истечении (Ма >1) давление на срезе сопла не зависит от величины противодавления и определяется начальным давлением в камере и процессом изменения состояния в сопле.
Расчетный режим истечения — частный случай равенства давлений на срезе сопла и в окружающей среде: ра = рИ (рис. 4.8, а). В таком сопле возникает результирующая сила (тяга) Рк, направленная в сторону, противоположную истечению и, в общем случае, пропорциональная XV — скорости движения жидкости вдали от выходного сечения сопла аппарата.
Истечение с недорасгиирением. В случае ра > р/, (рис. 4.8, б) происходит педорасширение до скорости XVа («укороченное» сопло), потеря энергии и недополучение требуемой тяги.
Истечение с перерасгиирением. В случае ра < рИ (рис. 4.8, б) происходит перерасширение, давление газовой струи на выходе из сопла становится равным давлению окружающей среды путем одного или нескольких скачков уплотнения. Максимум величины М7' приходится на расчетный режим, поскольку и при нерерасширении и скачках уплотнения скорость потока замедляется, а тяга Рк надает.

Рис. 4.8. Влияние режима истечения на величину реакции струи:
а — расчетный режим; б — истечение с недорасширением; в — истечение с перерасширением; ра — давление в выходном сечении сопла; р/, — давление в окружающей среде; Рк — результирующая сила (тяга)
|
|
|
|
 Скачать 208.54 Kb.
Скачать 208.54 Kb.