Курсовой. РТЦиС_Кр_18ПР3_РожковЕО. История создания гелийнеонового лазеров зарубежом и в ссср. Принцип действия
 Скачать 1.83 Mb. Скачать 1.83 Mb.
|
Приложение 3.МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ «УТВЕРЖДАЮ» Зав. кафедрой РТиРЭС д.т.н., профессор ______________А.В. Светлов ЗАДАНИЕ на курсовую работу по дисциплине «Радиотехнические цепи и сигналы» Тема: «Определение спектров модулированных колебаний» ВАРИАНТ 53-04 График модулирующего колебания  показан на рисунке З.1. показан на рисунке З.1.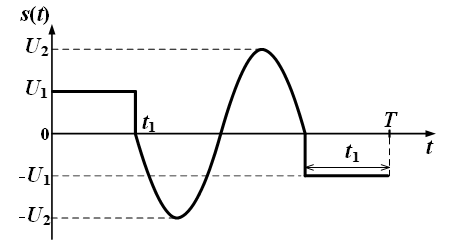 Рисунок З.1. Временная диаграмма заданного колебания Параметры заданного колебания: U1 = 4 В, t1 = 80 мкс, U2= 2 В, T = 400 мкс, где T - период колебания  ; t1, U1 – длительность и амплитуда прямоугольного видеоимпульса; U2 – амплитуда синусоидального колебания. ; t1, U1 – длительность и амплитуда прямоугольного видеоимпульса; U2 – амплитуда синусоидального колебания.РАСЧЕТНОЕ ЗАДАНИЕ Определить характеристики модулирующего колебания  согласно номеру колебания и номеру варианта индивидуального задания. согласно номеру колебания и номеру варианта индивидуального задания.Используя исходные данные, описать модулирующее колебание  на интервале, длительность которого равна периоду на интервале, длительность которого равна периоду  данного колебания, как кусочно-непрерывную функцию данного колебания, как кусочно-непрерывную функцию  времени. времени.Построить график кусочно-непрерывной функции  , сравнить его с графиком заданного модулирующего колебания. , сравнить его с графиком заданного модулирующего колебания.Описать периодическое продолжение кусочно-непрерывной функции 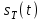 , определить частоту , определить частоту 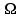 полученного периодического колебания полученного периодического колебания  . .Построить график периодического продолжения  кусочно-непрерывной функции кусочно-непрерывной функции 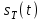 . .Используя формулы Фурье-Эйлера, разложить колебание  в тригонометрический ряд Фурье. в тригонометрический ряд Фурье. Определить постоянную составляющую 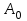 анализируемого колебания анализируемого колебания  . .Определить коэффициенты 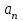 ряда Фурье, которые представляют синфазные амплитуды гармоник колебания ряда Фурье, которые представляют синфазные амплитуды гармоник колебания  Определить коэффициенты 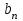 ряда Фурье, которые представляют квадратурные амплитуды ряда Фурье, которые представляют квадратурные амплитуды 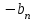 гармоник колебания гармоник колебания  с обратным знаком. Для колебания, которое описывается четной или нечетной функцией, а также для колебания с другим видом симметрии проверить полученные значения с обратным знаком. Для колебания, которое описывается четной или нечетной функцией, а также для колебания с другим видом симметрии проверить полученные значения 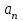 и и 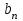 на их соответствие свойствам рядов Фурье симметричных колебаний. на их соответствие свойствам рядов Фурье симметричных колебаний.Результаты, полученные с помощью методов численного интегрирования, проверить, используя символические вычисления определенных интегралов. Определить амплитуды 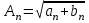 гармоник колебания гармоник колебания  . .Определить начальные фазы 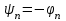 гармоник с обратным знаком с учетом номера квадранта, в котором находится вектор гармоник с обратным знаком с учетом номера квадранта, в котором находится вектор 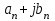 , где , где 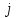 - мнимая единица. Проверить полученные результаты, определяя начальные фазы - мнимая единица. Проверить полученные результаты, определяя начальные фазы  гармоник как аргументы комплексных величин гармоник как аргументы комплексных величин 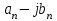 . Значения . Значения  и и  должны отличаться только знаком. должны отличаться только знаком.Построить графики амплитудно-частотной и фазо-частотной характеристик модулирующего колебания, учитывая, что постоянная составляющая характеризуется не начальной фазой, а знаком. Исследовать сходимость ряда Фурье. Аппроксимировать модулирующее колебание частичной суммой ряда Фурье 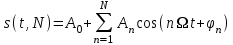 , где , где  - число гармоник частичной суммы. Исследовать сходимость ряда Фурье качественно, совместив графики функций - число гармоник частичной суммы. Исследовать сходимость ряда Фурье качественно, совместив графики функций  и и 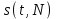 при различном числе при различном числе  гармоник в частичных суммах. Сделать выводы о сходимости ряда Фурье в среднем и в различных точках, обращая особое внимание на точки разрыва функции гармоник в частичных суммах. Сделать выводы о сходимости ряда Фурье в среднем и в различных точках, обращая особое внимание на точки разрыва функции  . .Для количественной оценки сходимости ряда Фурье в точках области определения функции  определить погрешность определить погрешность 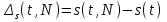 аппроксимации данной функции частичной суммой ряда Фурье как функцию времени и числа аппроксимации данной функции частичной суммой ряда Фурье как функцию времени и числа  слагаемых частичной суммы. Построить временные диаграммы данной погрешности при различном числе слагаемых частичной суммы. Построить временные диаграммы данной погрешности при различном числе  и оценить сходимость ряда в точках непрерывности, точках разрыва функции и ее производной, в положительных и отрицательных окрестностях точек разрыва при их наличии. и оценить сходимость ряда в точках непрерывности, точках разрыва функции и ее производной, в положительных и отрицательных окрестностях точек разрыва при их наличии.При наличии точек разрыва функции  построить графики зависимостей погрешности аппроксимации в точках разрыва, в положительной и отрицательной окрестностях точек построить графики зависимостей погрешности аппроксимации в точках разрыва, в положительной и отрицательной окрестностях точек 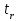 разрыва от числа разрыва от числа  . Сопоставить данные зависимости и сделать выводы о временной зависимости погрешности аппроксимации и сходимости ряда Фурье в окрестностях точек разрыва функции . Сопоставить данные зависимости и сделать выводы о временной зависимости погрешности аппроксимации и сходимости ряда Фурье в окрестностях точек разрыва функции  : :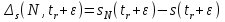 , , 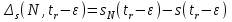 . (З.8.3) . (З.8.3)Построить график зависимости относительной среднеквадратической погрешности аппроксимации от числа  и сделать вывод о сходимости ряда Фурье колебания и сделать вывод о сходимости ряда Фурье колебания  в среднем: в среднем: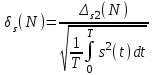 , (З.8.4) , (З.8.4)где  - среднеквадратическая погрешность. - среднеквадратическая погрешность.Определить мощности 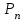 спектральных составляющих колебания спектральных составляющих колебания  - мощность - мощность 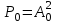 постоянной составляющей постоянной составляющей 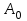 и мощности и мощности 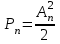 гармоник, построить график спектра мощности гармоник, построить график спектра мощности 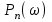 , , 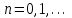 , данного колебания. , данного колебания.Рассчитать полную мощность 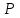 колебания колебания  , усредненную на его периоде, и долю , усредненную на его периоде, и долю  полной мощности, где полной мощности, где  - положительное число, меньшее единицы. Суммируя последовательно мощности спектральных составляющих, начиная с мощности - положительное число, меньшее единицы. Суммируя последовательно мощности спектральных составляющих, начиная с мощности 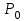 постоянной составляющей, и сравнивая получаемые суммы постоянной составляющей, и сравнивая получаемые суммы  с долей с долей 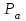 полной мощности полной мощности 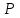 , определить эффективную ширину спектра , определить эффективную ширину спектра 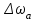 заданного колебания. Эффективная ширина спектра равна частоте заданного колебания. Эффективная ширина спектра равна частоте 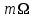 составляющей, при суммировании мощности которой значение составляющей, при суммировании мощности которой значение  становится не меньше значения становится не меньше значения 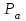 . Сопоставить график зависимости мощности . Сопоставить график зависимости мощности 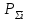 колебания, описываемого частичной суммой ряда Фурье, от числа колебания, описываемого частичной суммой ряда Фурье, от числа  суммируемых гармоник с уровнями полной мощности суммируемых гармоник с уровнями полной мощности 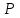 и ее доли и ее доли 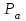 при различных значениях при различных значениях  . Сделать выводы о характере зависимости эффективной ширины спектра от той доли, которую составляет мощность колебания с ограниченным спектром в полной мощности колебания. . Сделать выводы о характере зависимости эффективной ширины спектра от той доли, которую составляет мощность колебания с ограниченным спектром в полной мощности колебания.Описать двухполосные амплитудно-модулированные колебания 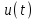 и и  , используя в качестве модулирующих сигналов заданное колебание , используя в качестве модулирующих сигналов заданное колебание  и его аналог и его аналог 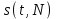 с ограниченным спектром. с ограниченным спектром.Задать несущую частоту 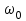 , которая должна быть не менее чем в два раза больше эффективной ширины , которая должна быть не менее чем в два раза больше эффективной ширины 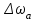 спектра модулирующего колебания. спектра модулирующего колебания.Определить амплитуду 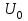 несущего колебания как величину, пропорциональную сумме амплитуд гармоник ограниченного спектра модулирующего колебания: несущего колебания как величину, пропорциональную сумме амплитуд гармоник ограниченного спектра модулирующего колебания: 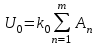 , где , где  - положительный коэффициент. - положительный коэффициент.Задать начальную фазу 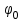 несущего колебания равной нулю при неотрицательной постоянной составляющей несущего колебания равной нулю при неотрицательной постоянной составляющей 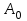 модулирующего колебания и модулирующего колебания и 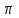 - при отрицательном значении - при отрицательном значении 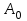 . .Описать модулированное колебание формулой  , (З.11.4) , (З.11.4)где 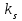 - коэффициент, характеризующий глубину модуляции, значение которого выбирается из условия - коэффициент, характеризующий глубину модуляции, значение которого выбирается из условия 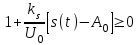 . Построить график модулированного колебания . Построить график модулированного колебания 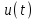 и сравнить формы огибающей данного колебания и модулирующего колебания и сравнить формы огибающей данного колебания и модулирующего колебания  . .Для записи колебания  , модулированного сигналом , модулированного сигналом 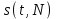 с ограниченным спектром, определить парциальные коэффициенты модуляции с ограниченным спектром, определить парциальные коэффициенты модуляции 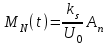 . .Описать колебание  , модулированное сигналом , модулированное сигналом 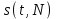 , формулой , формулой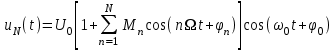 . (З.11.6) . (З.11.6)Построить графики колебаний при различных числах  и сделать вывод о характере изменения огибающей модулированного колебания при увеличении числа спектральных составляющих модулирующего сигнала. и сделать вывод о характере изменения огибающей модулированного колебания при увеличении числа спектральных составляющих модулирующего сигнала.Определить спектр двухполосного АМ-колебания, модулированного сигналом с ограниченным спектром. Вычислить амплитуды 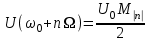 и начальные фазы и начальные фазы 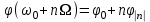 спектральных составляющих верхней ( спектральных составляющих верхней (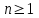 ) и нижней ( ) и нижней ( ) боковых полос (ВБП и НБП). ) боковых полос (ВБП и НБП).Проверить полученные значения 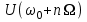 и и 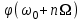 , для чего описать АМ-колебание как сумму его спектральных составляющих: , для чего описать АМ-колебание как сумму его спектральных составляющих: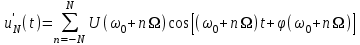 , (З.12.2) , (З.12.2)где 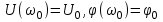 . Построить график колебания . Построить график колебания  и сравнить его с графиком колебания и сравнить его с графиком колебания  . .Используя полученные данные, построить спектры амплитуд и фаз АМ-колебания, модулированного сигналом с ограниченным спектром. Определить ширину спектра модулированного колебания  и сравнить полученное значение с шириной спектра модулирующего сигнала и сравнить полученное значение с шириной спектра модулирующего сигнала 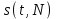 . .Определить энергетические характеристики двухполосного АМ-колебания, модулированного сигналом с ограниченным спектром. Определить мощности  спектральных составляющих, мощности спектральных составляющих, мощности 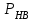 и и  верхней и нижней боковых полос, а также суммарную мощность верхней и нижней боковых полос, а также суммарную мощность 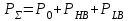 колебания колебания  : : , (З.13.1) , (З.13.1)где  . .Определить энергетический к.п.д. передатчика двухполосного АМ-колебания, модулированного сигналом с ограниченным спектром: 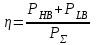 . (З.13.2) . (З.13.2)Определить характеристики колебания с балансной модуляцией, используя в качестве модулирующего сигнала периодическое колебание  и его аналог и его аналог 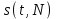 с ограниченным спектром. с ограниченным спектром.Представить колебание  с балансной модуляцией как результат перемножения несущего колебания и модулирующего сигнала без постоянной составляющей. Построить график данного колебания, сравнить формы его огибающих с графиком модулирующего сигнала с балансной модуляцией как результат перемножения несущего колебания и модулирующего сигнала без постоянной составляющей. Построить график данного колебания, сравнить формы его огибающих с графиком модулирующего сигнала  . Сделать вывод о характере изменения фазы высокочастотного заполнения в моменты пересечения переменной составляющей сигнала . Сделать вывод о характере изменения фазы высокочастотного заполнения в моменты пересечения переменной составляющей сигнала  нулевого уровня. нулевого уровня.Описать колебание 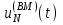 с балансной модуляцией как двухполосное амплитудно-модулированное колебание с подавленным несущим колебанием: с балансной модуляцией как двухполосное амплитудно-модулированное колебание с подавленным несущим колебанием: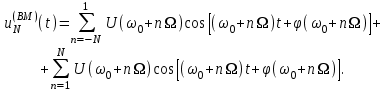 (З.14.2) (З.14.2)Построить графики данного колебания для различных чисел  и сравнить формы полученных огибающих с огибающей колебания и сравнить формы полученных огибающих с огибающей колебания  . .Определить спектр амплитуд и фаз колебания с балансной модуляцией, учитывая, что в спектре данного колебания отсутствует несущее колебание. Построить соответствующие спектральные диаграммы. Определить ширину спектра колебания  с балансной модуляцией как разницу верхней и нижней граничных частот. Сравнить полученное значение с шириной спектра модулирующего сигнала с балансной модуляцией как разницу верхней и нижней граничных частот. Сравнить полученное значение с шириной спектра модулирующего сигнала 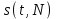 . .Используя значения мощностей нижней и верхней боковых полос 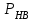 и и  двухполосного амплитудно-модулированного колебания, определить полную мощность двухполосного амплитудно-модулированного колебания, определить полную мощность 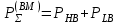 колебания с балансной модуляцией как сумму мощностей его боковых полос и коэффициент полезного действия передатчика данного колебания. колебания с балансной модуляцией как сумму мощностей его боковых полос и коэффициент полезного действия передатчика данного колебания.Определить характеристики однополосного амплитудно-модулированного колебания с верхней боковой полосой (ВБП), используя в качестве модулирующего сигнала периодическое колебание 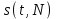 с ограниченным спектром. с ограниченным спектром.Описать однополосное амплитудно-модулированное колебание с ВБП во временной области как сумму несущего и верхних боковых колебаний: 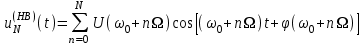 . (З.15.1) . (З.15.1)Построить график данного колебания и сравнить форму его огибающей с графиком модулирующего сигнала. Определить спектры амплитуд и фаз однополосного колебания с ВБП, учитывая, что в спектре данного колебания отсутствует НБП. Построить соответствующие спектральные диаграммы. Определить ширину спектра однополосного колебания 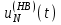 с ВБП как разницу верхней и нижней граничных частот. Сравнить полученное значение с шириной спектра модулирующего сигнала с ВБП как разницу верхней и нижней граничных частот. Сравнить полученное значение с шириной спектра модулирующего сигнала 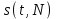 . .Определим полную мощность 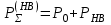 однополосного колебания с ВБП как сумму мощностей несущего колебания и верхней боковой полосы, а также коэффициент полезного действия передатчика данного колебания, учитывая, что информация о модулирующем сигнале переносится только составляющими верхней боковой полосы модулированного колебания, а несущее колебание передается в неизменном виде даже при отсутствии сигнала сообщения. однополосного колебания с ВБП как сумму мощностей несущего колебания и верхней боковой полосы, а также коэффициент полезного действия передатчика данного колебания, учитывая, что информация о модулирующем сигнале переносится только составляющими верхней боковой полосы модулированного колебания, а несущее колебание передается в неизменном виде даже при отсутствии сигнала сообщения.Определить характеристики однополосного амплитудно-модулированного колебания с верхней боковой полосой (ВБП) и подавленным несущим, используя в качестве модулирующего сигнала периодическое колебание 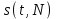 с ограниченным спектром. с ограниченным спектром.Описать однополосное амплитудно-модулированное колебание 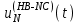 с ВБП и подавленным несущим во временной области как сумму верхних боковых колебаний: с ВБП и подавленным несущим во временной области как сумму верхних боковых колебаний: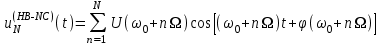 . (З.16.2) . (З.16.2)Построить график данного колебания и сравнить форму его огибающей с графиком модулирующего сигнала. Определить спектр амплитуд колебания 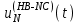 , учитывая, что в спектре данного колебания отсутствуют нижние боковые и несущее колебания. Построить спектральные диаграммы амплитудно-модулированного колебания с ВБП и подавленным несущим. , учитывая, что в спектре данного колебания отсутствуют нижние боковые и несущее колебания. Построить спектральные диаграммы амплитудно-модулированного колебания с ВБП и подавленным несущим.Определить ширину спектра колебания 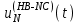 как разницу верхней и нижней граничных частот и полученное значение с шириной спектра модулирующего сигнала как разницу верхней и нижней граничных частот и полученное значение с шириной спектра модулирующего сигнала 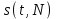 . .Определить полную мощность 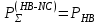 однополосного колебания с ВБП и подавленным несущим как мощность верхней боковой полосы, а также коэффициент полезного действия передатчика данного колебания, учитывая, что информация о модулирующем сигнале переносится составляющими верхней боковой полосы модулированного колебания. однополосного колебания с ВБП и подавленным несущим как мощность верхней боковой полосы, а также коэффициент полезного действия передатчика данного колебания, учитывая, что информация о модулирующем сигнале переносится составляющими верхней боковой полосы модулированного колебания.ЗАДАНИЕ ПО МОДЕЛИРОВАНИЮ* Используя систему «Matlab+Simulink», построить структурно-функциональные модели генератора модулирующего колебания, амплитудных модуляторов и детекторов для формирования и демодуляции сигналов с двухполосной, балансной, однополосной (ВБП) модуляцией, однополосной (ВБП) модуляцией с подавленным несущим колебанием. Характеристики моделируемых узлов – генератора, модуляторов и детекторов следует выбирать в соответствии с заданием на курсовую работу и результатами расчетов. Сравнить результаты моделирования в виде временных и спектральных диаграмм модулирующего колебания, модулированных сигналов и результатов их детектирования с результатами расчетов по пунктам 3 – 16 расчетного задания. ЗАДАНИЕ ПО РАЗРАБОТКЕ ВИРТУАЛЬНЫХ ПРИБОРОВ* Используя среду графического программирования LabVIEW, разработать и виртуальные приборы (ВП) генератора модулирующего колебания, амплитудных модуляторов и детекторов для формирования и демодуляции сигналов с двухполосной, балансной, однополосной (ВБП) модуляцией, однополосной (ВБП) модуляцией с подавленным несущим колебанием. Характеристики ВП – генератора, модуляторов и детекторов следует выбирать в соответствии с заданием на курсовую работу и результатами расчетов. Используя разработанные ВП в качестве виртуальных подприборов (ВПП), объединить их в ВП более высокого уровня. Сравнить результаты работы ВП в виде временных и спектральных диаграмм модулирующего колебания, модулированных сигналов и результатов их детектирования с результатами расчетов по пунктам 3 – 16 расчетного задания. Руководитель работы, доцент _______________ С.К. Куроедов 7 сентября 2020 г. Задание получил, студент группы 18ПР-3 ____________ Е.О. Рожков 7 сентября 2020 г. Примечание: Дополнительные разделы задания отмечены звездочкой * |
