Курсовой. РТЦиС_Кр_18ПР3_РожковЕО. История создания гелийнеонового лазеров зарубежом и в ссср. Принцип действия
 Скачать 1.83 Mb. Скачать 1.83 Mb.
|
Основная часть1. Определение и анализ спектров модулирующего сигналаПараметры заданного колебания: U1 = 4 В, U2 = 2 В, t1 = 80 мкс, T = 400 мкс, где T - период колебания  ; t1 и U1 – длительность и амплитуда положительного и отрицательного прямоугольных видеоимпульсов; U2 – амплитуда волны противофазного синусоидального колебания. ; t1 и U1 – длительность и амплитуда положительного и отрицательного прямоугольных видеоимпульсов; U2 – амплитуда волны противофазного синусоидального колебания.Oпишем колебание 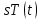 нa интервале oт 0 дo T, используя операторы Add Line и if. Данное описание представлено формулой (3): нa интервале oт 0 дo T, используя операторы Add Line и if. Данное описание представлено формулой (3):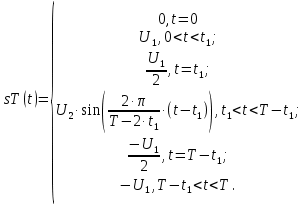 (3) (3)Построим график модулирующего колебания 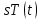 . График изображён на рис. 1. . График изображён на рис. 1.  Рис. 1. График модулирующего колебания sT(t) Функция является непрерывной, периодической. Колебание имеет три точки разрыва в моменты времени 0, 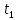 и и 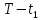 . .Построим график периодического продолжения 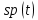 колебания колебания 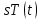 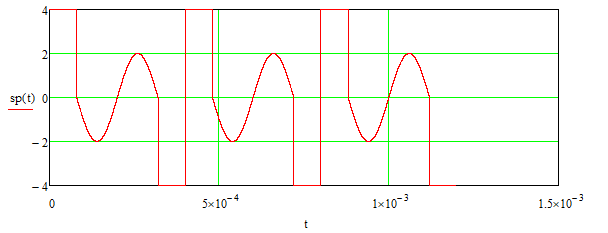 Рис. 2. График периодического продолжения Рис. 2. График периодического продолжения 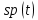 колебания колебания 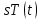 Разложим колебание 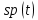 в ряд Фурье и определяем его коэффициенты в ряд Фурье и определяем его коэффициенты 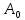 , , 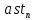 , , 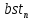 по формулам Фурье-Эйлера . по формулам Фурье-Эйлера .Вычисление постоянной составляющей 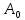 осуществляется по формуле (4): осуществляется по формуле (4):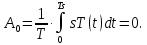 (4) (4)Вычисление синфазных амплитуд 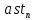 гармоник осуществляется по формуле (5): гармоник осуществляется по формуле (5):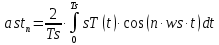 (5) (5)Вычисление квадратурных амплитуд 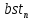 гармоник осуществляется по формуле (6): гармоник осуществляется по формуле (6):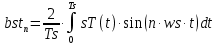 (6) (6)Полученные в результате численного интегрирования значения коэффициентов синфазных и квадратурных амплитуд отличны от нуля. Значения синфазных и квадратурных амплитуд, а также амплитуд 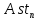 и неполных фаз и неполных фаз 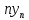 гармоник приведены в приложении 1 (стр. 34-36). гармоник приведены в приложении 1 (стр. 34-36).График амплитудно-частотной характеристики модулирующего колебания изображён на рис. 3. 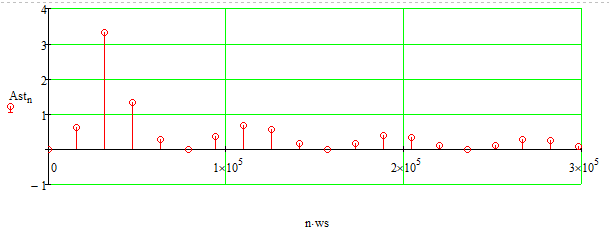 Рис. 3. График АЧХ модулирующего колебания График фазочастотной характеристики модулирующего колебания изображён на рис. 4. 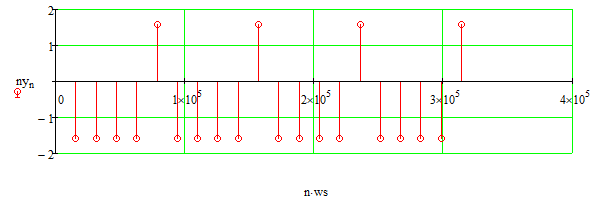 Рис. 4. График ФЧХ модулирующего колебания Для проверки получившихся результатов, графики модулирующего колебания 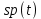 и частичной суммы ряда Фурье и частичной суммы ряда Фурье 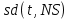 отображаются на одном графике, при различных значениях числа гармоник NS. Данные графики отображены в Приложении 1 (с. 37-38). отображаются на одном графике, при различных значениях числа гармоник NS. Данные графики отображены в Приложении 1 (с. 37-38).При сравнении графиков заданного колебания 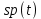 и частичной суммы рядa Фурье и частичной суммы рядa Фурье 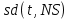 , при различном числе , при различном числе 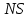 , можно сделать вывод о сходимости рядa Фурье в области определения , можно сделать вывод о сходимости рядa Фурье в области определения 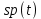 среднем и вo всех точках. среднем и вo всех точках.Для количественной оценки сходимости ряда Фурье определяется погрешность аппроксимации колебания частичной суммой членов этого ряда как функцию времени и числа членов ряда, затем строятся временные диаграммы погрешности 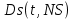 при различных значениях числа членов ряда. Графики временных диаграмм погрешности аппроксимации при различных значениях числа членов ряда отображены в Приложении 1 (с. 39-41). при различных значениях числа членов ряда. Графики временных диаграмм погрешности аппроксимации при различных значениях числа членов ряда отображены в Приложении 1 (с. 39-41).По графикам временных диаграмм, можно сделать вывод о том, что погрешность аппроксимации с ростом числа членов ряда Фурье в его частичной сумме, уменьшается во всех точках непрерывности модулирующего колебания за исключением точек в положительных и отрицательных окрестностях точек разрыва. В окрестностях точек разрыва наблюдаются выбросы погрешности 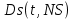 , длительности которых с увеличением числа NS членов ряда уменьшается, a амплитуды при достаточно большом значении NS практически не изменяются. , длительности которых с увеличением числа NS членов ряда уменьшается, a амплитуды при достаточно большом значении NS практически не изменяются.Для анализа сходимости ряда Фурье в среднем определяется относительная среднеквадратичная погрешность 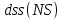 аппроксимации колебания аппроксимации колебания 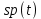 частичной суммой ряда Фурье как функция числа членов ряда. График зависимости частичной суммой ряда Фурье как функция числа членов ряда. График зависимости 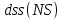 показан на рис.5. показан на рис.5.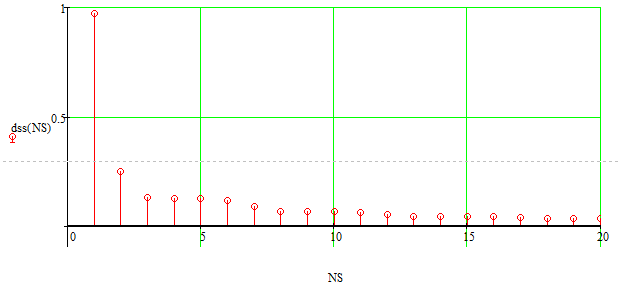 Рис. 5. График зависимости относительной среднеквадратической погрешности аппроксимации колебания частичной суммой ряда Фурье от числа слагаемых По данному графику, можно сделать вывод о том, что при увеличении числа членов ряда среднеквадратическая погрешность аппроксимации модулирующего колебания частичной суммой ряда Фурье монотонно уменьшается, асимптотически стремясь к нулю. Это свидетельствует о сходимости ряда Фурье в среднем. Мощность 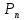 каждой спектральной составляющей определяется как ее энергия, усреднённая на периоде каждой спектральной составляющей определяется как ее энергия, усреднённая на периоде 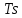 колебания. колебания. Мощность 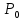 постоянной составляющей постоянной составляющей 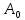 определяется по формуле (7): определяется по формуле (7):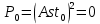 . (7) . (7)Значения мощностей спектральных составляющих гармоник приведены в Приложении 1 (с. 42). График спектра мощности 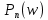 колебания колебания 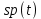 изображён на рис. 6. изображён на рис. 6.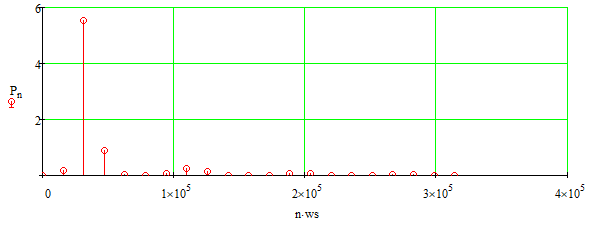 Рис. 6. График спектра мощности 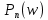 Для того чтобы определить эффективную ширину 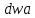 спектра модулирующего колебания по уровню спектра модулирующего колебания по уровню 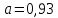 от полной мощности, рассчитывается полная мощность от полной мощности, рассчитывается полная мощность 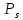 колебания по формуле (8) и её доля колебания по формуле (8) и её доля 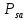 по формуле (9). по формуле (9). 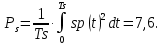 (8) (8)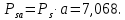 (9) (9)График зависимости суммы 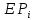 мощностей спектральных составляющих колебания мощностей спектральных составляющих колебания 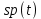 от числа i его гармоник изображён на рис.7. от числа i его гармоник изображён на рис.7.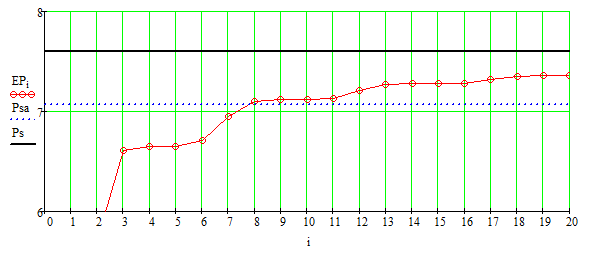 Рис. 7. График зависимости суммы мощностей спектральных составляющих модулирующего колебания от числа гармоник Из графика зависимости суммы мощностей спектральных составляющих колебания от числа его гармоник, следует, что при 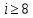 - EPiне меньше Psa. Следовательно, суммарная мощность постоянной составляющей и первых восьми гармоник составляет не менее 93% от полной мощности колебания. При увеличении числа спектральных составляющих модулирующего колебания их суммарная мощность стремится к полной мощности данного колебания, что является следствием равенства Парсиваля. - EPiне меньше Psa. Следовательно, суммарная мощность постоянной составляющей и первых восьми гармоник составляет не менее 93% от полной мощности колебания. При увеличении числа спектральных составляющих модулирующего колебания их суммарная мощность стремится к полной мощности данного колебания, что является следствием равенства Парсиваля. |
