Изгиб. Изгиб. Расчеты на прочность и жесткость при изгибе 10. 1 Чистый изгиб
 Скачать 287.47 Kb. Скачать 287.47 Kb.
|
Изгиб. Расчеты на прочность и жесткость при изгибе10.1 Чистый изгибРасчетные формулы для определения нормальных напряжений при изгибе обычно выводят из рассмотрения плоского чистого изгиба, который является наиболее простым случаем изгиба (рис.10.1).  Рис. 10.1 Плоский чистый изгиб Чистый изгиб – такой вид нагружения, при котором в поперечных сечениях бруса возникают только изгибающие моменты Мх, а Q=0. Чистый изгиб характерен тем, что из шести компонентов внутренних усилий только изгибающий момент не равен 0, а поперечные и нормальные силы отсутствуют. Для тех участков стержня, где соблюдается это условие, изгибающий момент остается постоянным (М = const). Изгибающий момент численно равен сумме моментов всех внешних сил, действующих на отсеченную часть балки относительно оси Ох. Эпюра изгибающих моментов строится на сжатом волокне. При этом изгибающий момент в балках считается положительным, если сжаты верхние волокна, т. е. элемент изгибается выпуклостью вниз. Рассмотрим три стороны задачи об изгибе: 1. Статическая сторона задачи: Условия чистого изгиба могут возникать при различных внешних нагрузках. Характерный пример показан на рисунке (простейший двухопорный стержень, нагруженный силами Р) (рис. 10.2). 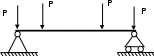  M   Чистый изгиб Рис. 10.2 Напряжения при чистом изгибе Рассмотрим условие равновесия, связывающее напряжения и внутренние усилия в поперечном сечении балки (рис. 10.3), опуская индекс x y момента, получим 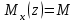 (1) (1)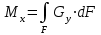 (2) (2)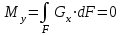 (3) (3)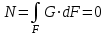 (4) (4)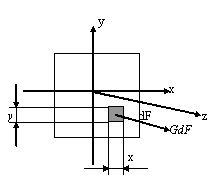 Рис. 10.3 Поперечное сечение балки 2. Геометрическая сторона задачи: При изгибе под действием моментов М ось балки искривляется (установлено экспериментально). 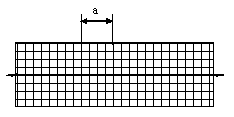 Рис. 10.4 Сетка, предварительно нанесенная на балку Наблюдая за деформацией сетки, предварительно нанесенной на балку (рис. 10.4), можно заметить, что продольные линии при чистом изгибе искривляются по дуге окружности, контуры поперечных сечений остаются плоскими кривыми, пересекая продольные линии под прямыми углами (рис. 10.5). Это говорит о том, что при чистом изгибе поперечные сечения остаются плоскими и, поворачиваясь, становятся нормальными к изогнутой оси балки. Фактически это есть доказательство того, что все сечения однородной балки при чистом изгибе не искривляются, а лишь поворачиваются. Это утверждение, будучи точным, для чистого изгиба, в общем случае является приближенным и именуется гипотезой плоских сечений (Бернулли). 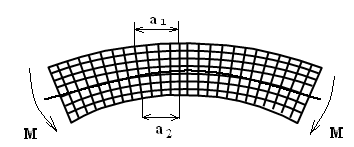 Рис. 10.5 Деформация участка балки при чистом изгибе Поворот плоских поперечных сечений одного относительно другого является результатом образования деформаций при чистом изгибе. В сжатой области (сверху) волокна укорачиваются, а в зоне растяжения удлиняются. Зона растяжения в сечении балки разделяются нейтральным слоем с радиусом кривизны ρ. Длина нейтрального слоя при изгибе остается неизменной. Рассмотрим два смежных сечения a и b, расположенных между собой на расстоянии dz (рис. 10.6). Предположим, что левая часть неподвижна, а правая поворачивается относительно левого участка. 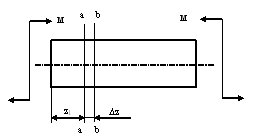 Рис. 10.6 Поворот правого участка относительно левого При чистом изгибе найдем из рассмотрения деформации участка балки длиной dz относительное удлинение некоторого волокна, находящегося на расстоянии у от нейтрального слоя 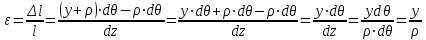 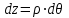 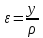 (5) -относительное удлинение участка (5) -относительное удлинение участка3. Физическая сторона задачи: При чистом изгибе вводится предположение о ненадавливаемости продольных слоев (рис.10.7). 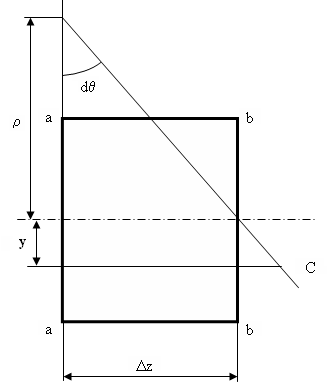 Рис. 10.7 Деформация участка балки длиной dz = 0 – касательное напряжение 0 – нормальное напряжение Так как = 0, то это значит, что волокна балки находятся в линейно напряженном состоянии  (6) - применяем закон Гука (6) - применяем закон Гука4. Объединяем три стороны задачи: (5)(6) 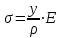 (7) (7)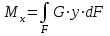 (7)(2)  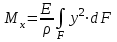 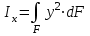 - осевой момент инерции, зависит от формы, размеров. - осевой момент инерции, зависит от формы, размеров.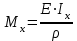 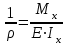 (8), где Е∙Ix - жесткость сечения при изгибе (8), где Е∙Ix - жесткость сечения при изгибеИзменяется по высоте сечения по линейному закону: 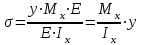 Напряжения при изгибе: 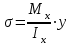  (9) – нормальные напряжения при изгибе. (9) – нормальные напряжения при изгибе.Рис. 10.8 Сечение не имеющее горизонтальной оси симметрии Максимальное напряжение при изгибе возникает в точках, наиболее удаленных от нейтральной линии. 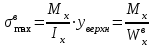 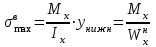 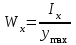 - осевой момент сопротивления сечения - осевой момент сопротивления сечения(9)(4) 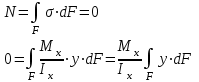 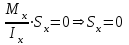 - статический момент инерции - статический момент инерцииЗначит, ось х – центральная. Таким образом, центр инерции проходит через центр тяжести сечения. 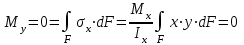 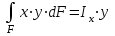 - центробежный момент инерции - центробежный момент инерции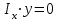 Через ось у проходит силовая плоскость, значит, оси x и у – главные центральные оси. Мы получили условия существования прямого изгиба (когда деформирование бруса происходит в силовой плоскости). Для сечений с двойной симметрией унижн=уверхн=уmax 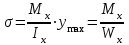 , где , где 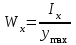 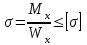 - условие прочности при изгибе. - условие прочности при изгибе.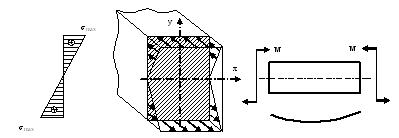  Рис. 10.9 Эпюра нормальных напряжений и сечение с горизонтальной осью симметрии Пример (Рис. 10.10) П 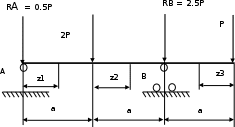 одобрать номер двутавра одобрать номер двутавраРис. 10.10 Расчетная схема Дано: P=40 кН A=1 м []=160 МПа Решение: Растяжение – сжатие: 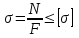 Кручение: 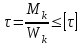 Изгиб: 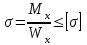 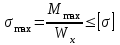 - условие «экономичности» - условие «экономичности»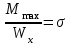 , , 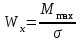 Строим эпюры Q и M (рис. 10.11)(эпюра М строится на сжатых волокнах) Q     2P RA    RB M   Рис. 10.11 Построение эпюр Q и M Для этого определяем реакции RA,RB, используя уравнения равновесия 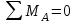 , , 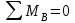 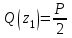 , ,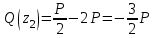 , ,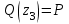 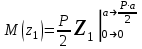 , , 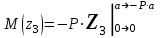 Опасное сечение над опорой В 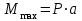 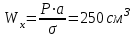 Двутавр №22, 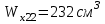 Для №22 перегрузка 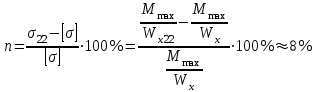 Пример (И-1) Для балки (Рис. 10.12) из расчета на прочность по нормальным напряжениям подобрать сечение в двух вариантах а) двутавровое б) полый прямоугольник. Проверить прочность балки по касательным напряжениям для двух вариантов. Построить эпюру касательных напряжений для прямоугольного сечения. Определить вертикальное перемещение сечения С. сравнить вес балок с прямоугольным и двутавровым сечением.  Рис. 10.12 Прямоугольное полое сечение и расчетная схема y 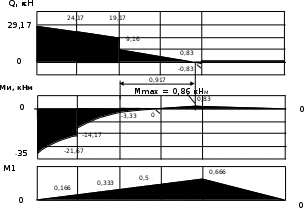 Рис.10.13 Построение эпюр Q и M Дано: 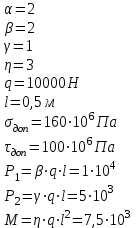 Решение: Y: 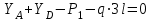 (у правой) 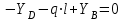 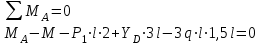 (MD правой) 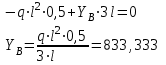 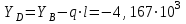 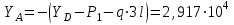 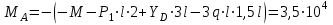 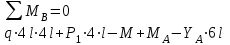     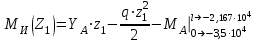 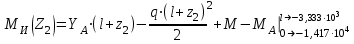 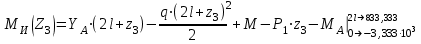 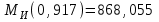 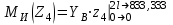 На третьем участке определяем максимум для момента: 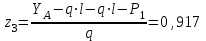 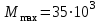 Находим величину момента сопротивления: 1)для двутавра 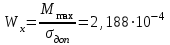 подбираем номер двутавра №22 Wx.22=232·10-6 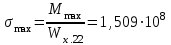 Проверка: 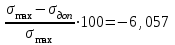 % (недонапряжение) % (недонапряжение)Подбираем номер двутавра №20а Wx.20а=203·10-6 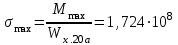 Проверка: 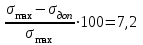 % (перенапряжение) % (перенапряжение)Т.к. на практике допускаются перенапряжения до 5 %, то выбираем № 22 2)для специального сечения 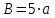 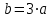 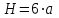 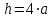 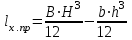 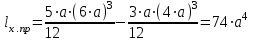 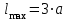 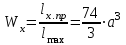  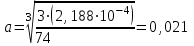 м м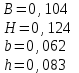 Определим площадь этого сечения: 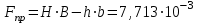 м2 м2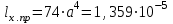 Проверим прочность балки по касательным напряжениям для двух вариантов сечений: 1)для двутавра 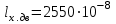 м м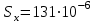 м м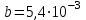 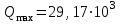 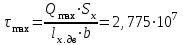 Па (меньше τдоп) Па (меньше τдоп)Двутавр удовлетворяет требованиям прочности 2)для прямоугольника τ1=0 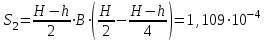 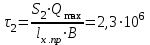 Па Па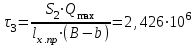 Па Па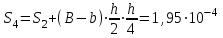 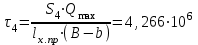 Па Па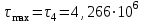 Па ПаОпределим вертикальное перемещение в сечении с: 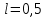 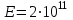 Па Па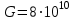 Па Па1-й участок 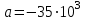 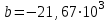 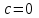 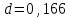 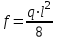 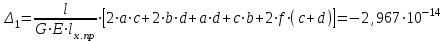 2-й участок     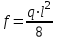 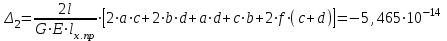 3-й участок  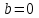 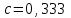 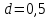 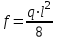 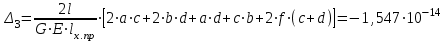 4-й участок 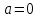 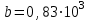 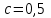 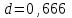 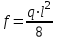 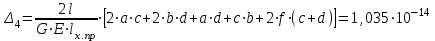 5-й участок 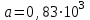 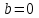 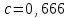  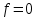 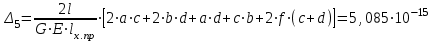 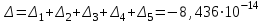 Определяем металлоемкость: 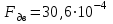 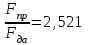 Таким образом, балка двутаврового сечения обладает меньшей металлоемкостью, чем балка в виде прямоугольника(рис.10.14 и рис.10.15).  Рис. 10.14 Эпюра касательных напряжений для прямоугольного сечения  y max 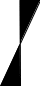      max = 27.75Па max Рис. 10.15 Двутаврное сечение балки 10.2 Поперечный изгибПоперечный изгиб – это такой вид нагружения, при котором в поперечных сечениях бруса возникают не только изгибающие моменты Мх, но и поперечные силы Qу. Эта сила представляет собой равнодействующую элементарных распределенных сил, лежащих в плоскости сечения. В этом случае в поперечных сечениях возникают не только нормальные, но и касательные напряжения. 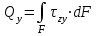 Возникновение касательных напряжений τ сопровождается появлением угловых деформаций. Поэтому, кроме основных смещений, свойственных чистому изгибу, каждая элементарная площадка сечения dF получает еще некоторые дополнительные угловые смещения, обусловленные сдвигом (рис. 10.16). 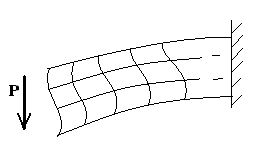 Рис. 10.16 Искривление поперечных сечений Касательные напряжения распределены по сечению неравномерно, поэтому неравномерно будут распределены и угловые смещения. Это значит, что при поперечном изгибе в отличие от чистого изгиба поперечные сечения не остаются плоскими. Найдем закон изменения касательных напряжений zy= при поперечном изгибе. Для этого сначала рассмотрим случаи поперечного изгиба (рис. 10.17): 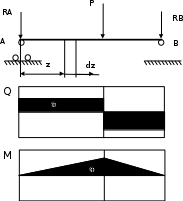 Рис. 10.17 Эпюры Q и M при поперечном изгибе Вычислить касательные напряжения проще всего через парные им напряжения, возникающие в продольных сечениях стержня. Выделим из бруска элемент длиной dz (рис. 10.18).  Нейтральный слой Рис. 10.18 Распределение касательных напряжений элемента бруска При поперечном изгибе моменты, возникающие в левом и правом сечениях элемента, не одинаковы и отличаются на dM. Продольным горизонтальным сечением, проведенным на расстоянии у от нейтрального слоя, разделим элемент на две части и рассмотрим условия равновесия верхней части. Равнодействующая нормальных сил 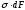 в левом сечении в пределах заштрихованной площади (отсеченной части) равна в левом сечении в пределах заштрихованной площади (отсеченной части) равна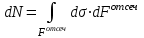 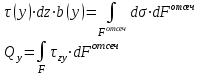 Полагая, что справедливо распределение в виде: 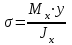 , получим , получим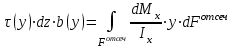 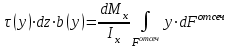 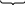 , ,где через у обозначена текущая ордината площадки dF. Разность нормальных сил в правом и левом сечении должна уравновешиваться касательными силами, возникающими в продольном сечении элемента (рис. 10.19) 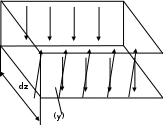 Рис. 10.19 Распределение касательных напряжений τ(у) на участке dz Полученный интеграл представляет собой статистический момент относительно оси х части площади, расположенной выше продольного сечения. Обозначим этот статистический момент через 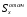 , тогда , тогда 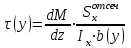 Учитывая, что 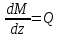 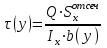 Полученная формула носит название формулы Журавского. Она позволяет вычислить касательные напряжения, возникающие в продольных сечениях стержня. 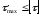 Полный расчет балки на прочность при поперечном изгибе: 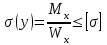 и 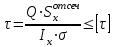 , ,где Iх – осевой момент инерции сечения относительно центральной оси х; b(y) – ширина живого сечения на уровне у; Sхотсеч – статический момент площади, отсеченной уровнем у. Пример Н  айти закон изменения касательного напряжения у на уровне у (рис. 10.20). айти закон изменения касательного напряжения у на уровне у (рис. 10.20).Рис. 10.20 Расчетная схема 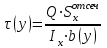 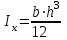 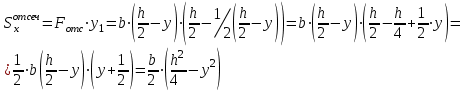 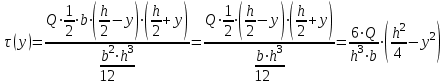 Закон изменения представляет собой параболу. 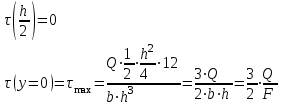  F |
