Гидравлика курсовая работа. курсовая 1. Изм Лист докум
 Скачать 379.54 Kb. Скачать 379.54 Kb.
|
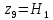 , ,  . Предположим, что по трубопроводу течёт идеальная жидкость, что позволяет не учитывать потери напора . Предположим, что по трубопроводу течёт идеальная жидкость, что позволяет не учитывать потери напора 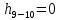 . . ; ;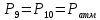 так как емкости открытые. так как емкости открытые.Запишем уравнение Бернулли (25) с учетом всех утверждений:  Зная расход можно определить  : : Подставляя (27) в (26), получим:  В действительности при прохождении жидкости в ёмкости через насадок возникают потери напора, учтём их с помощью коэффициента расхода 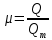 , подставив его в формулу (28): , подставив его в формулу (28):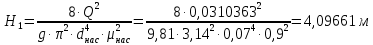 3.6Определение разности показания манометров Для сечений 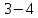 уравнение Бернулли имеет вид: уравнение Бернулли имеет вид: 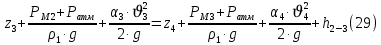 где 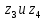 - расстояние от сечений - расстояние от сечений 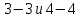 соответственно до некоторой произвольно выбранной горизонтальной плоскости; соответственно до некоторой произвольно выбранной горизонтальной плоскости; - давления в сечениях - давления в сечениях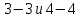 соответственно; соответственно;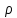 - плотность циркулирующей жидкости; - плотность циркулирующей жидкости;g - ускорение свободного падении;  - скорость течения жидкости в сечениях - скорость течения жидкости в сечениях 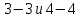 соответственно; соответственно; - коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях - коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях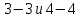 соответственно; соответственно; - потери напора на участках между выбранными сечениями. - потери напора на участках между выбранными сечениями.Выберем ось трубопровода за начало отсчета, тогда  , так как трубопровод горизонтален. , так как трубопровод горизонтален.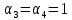  , так как расход и площадь поперечного сечения одинаковы для сечений , так как расход и площадь поперечного сечения одинаковы для сечений 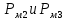 . В итоге формула (29) примет вид: . В итоге формула (29) примет вид: Потери напора по длине трубопровода определяется по формуле Дарси - Вейсбаха:  Подставим (31) в (30): 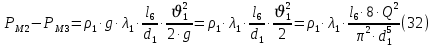  3.7Определение суммарных потерь напора в местных сопротивлениях Потери напора в местных сопротивлениях складываются из потерь на фланце, в угольниках, расходомера Вентури, на задвижках и выходе из трубы. Из справочника найдём значения коэффициента местных сопротивлений:  Запишем формулу Вейсбаха для нагнетательной линии:  где − n количество местных сопротивлений на рассматриваемом участке. В нашем случае имеем:  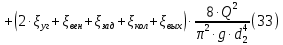   Потери напора в местных сопротивлениях можно выразить через эквивалентную длину, т.е. такую длину трубопровода, для которой 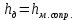 и и  Суммарная эквивалентная длина определяется по формуле:    3.8Определение необходимого диаметра самотечного трубопровода Для определения 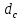 используется графоаналитический способ решения с использованием ПК (программа MicrosoftExcel). Задаемся интервалом используется графоаналитический способ решения с использованием ПК (программа MicrosoftExcel). Задаемся интервалом 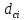 от 1 мм до 200 мм с шагом 5 мм. И для каждого варианта рассчитываются потери напора, возникающие при прохождении жидкости по самотечному трубопроводу. от 1 мм до 200 мм с шагом 5 мм. И для каждого варианта рассчитываются потери напора, возникающие при прохождении жидкости по самотечному трубопроводу.Потери напора определяются по формуле: 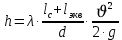 где 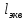 - суммарная эквивалентная длина местных сопротивлений самотечного трубопровода. - суммарная эквивалентная длина местных сопротивлений самотечного трубопровода.По результатам вычисления ПК 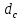 составить таблицу и построить график зависимости h=f( составить таблицу и построить график зависимости h=f(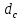 ). ).Где требуется найти: 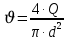 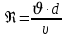 для ламинарного режима движения,  2000/2300 2000/2300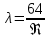 для турбулентного режима движения (формула Альтшуля),  2000/2300 2000/2300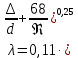 Пример расчета: Вычислим поэтапно потери напора для  =5мм =5мм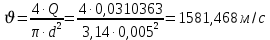 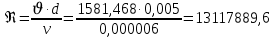 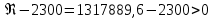 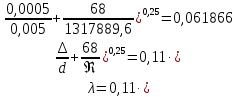 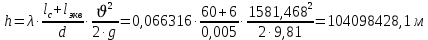 Таблица 3 –Таблица вычисленных потерь напора
Продолжение таблицы 3
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
