Гидравлика курсовая работа. курсовая 1. Изм Лист докум
 Скачать 379.54 Kb. Скачать 379.54 Kb.
|
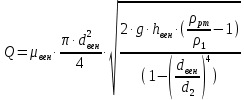 (10) (10)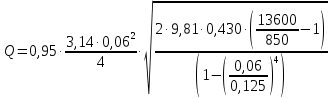 = 0,0310363 = 0,0310363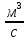 3.1.2 Определение потерь напора Определение величины потерь напора при движении реальных жидкостей является одной из основных задач практической гидравлики. При движении реальной жидкости энергия движения (напор) жидкости будет убывать по направлению движения. Причиной этого являются затраты энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости. В гидравлике различают два основных вида сопротивлений: местные потери напораи потери напора по длине, т.е. сопротивления, проявляющиеся по всей длине потока, обусловленные силами трения частиц жидкости друг о друга и о стенки, ограничивающие поток. Это линейные потери. Они определяются по формуле Дарси-Вейсбаха: 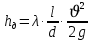 (11) (11)где 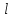 - длина трубы (или участка трубы) на котором определяются потери напора; - длина трубы (или участка трубы) на котором определяются потери напора;d - диаметр трубы; 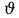 – средняя скорость в трубе; – средняя скорость в трубе;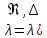 /d) – коэффициент гидравлического сопротивления трения. /d) – коэффициент гидравлического сопротивления трения.Коэффициент гидравлического сопротивления трения ( 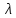 ) зависит от двух безразмерных параметров Rе – числа Рейнольдса и ) зависит от двух безразмерных параметров Rе – числа Рейнольдса и 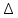 /d–относительной шероховатости трубы. Число Рейнольдса определяется по формуле: /d–относительной шероховатости трубы. Число Рейнольдса определяется по формуле: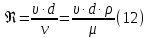 где, 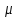 - динамическая вязкость жидкости, Па - динамическая вязкость жидкости, Па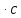 ; ;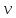 - кинематическая вязкость жидкости, - кинематическая вязкость жидкости, 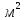 /c; /c;Для определения коэффициента гидравлического сопротивления трения существуют много различных формул. Удобно пользоваться следующими формулами. Для ламинарного режима движения: 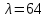 /Re, Re<2000/2300 /Re, Re<2000/2300Для турбулентного режима движения (формула Альтшуля): 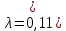 68/Re+ 68/Re+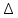 /d /d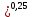 , Re> 2000/2300 , Re> 2000/2300Местные потери напора, так называемые местные сопротивления, обусловленные различного рода препятствиями, устанавливаемыми в потоке (задвижка, кран, колено), приводящими к изменениям в величине или направлении скорости течения жидкости. Потери напора на местных сопротивлениях определяются по формуле: 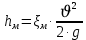 (13) (13)где 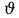 - средняя скорость движения жидкости; - средняя скорость движения жидкости; 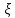 – коэффициент местного сопротивления. – коэффициент местного сопротивления.Потеря напора на местном сопротивлении может определяться как по скорости до местного сопротивления, так и по скорости после местного сопротивления. Так как скорости по величине могут быть разными, то в этих случаях для одного и тогоже местногосопротивления будут разные значения 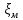 . Принято определять потери напора по скорости после местного сопротивления. Исключение составляет расширение трубопровода (выход потока из трубы в бак), где потери определяются по скорости до местного сопротивления. . Принято определять потери напора по скорости после местного сопротивления. Исключение составляет расширение трубопровода (выход потока из трубы в бак), где потери определяются по скорости до местного сопротивления.Для определения потерь напора по данной курсовой работе будем учитывать, как потери напора по длине трубопровода, так и местные сопротивления. 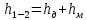 (14) (14)где 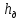 - потери напора по длине трубопровода, м; - потери напора по длине трубопровода, м;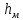 - потери напора от местных сопротивлений. - потери напора от местных сопротивлений.а) Вначале определим 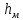 – потери напора от местных сопротивлений. Для этого сложим все местные сопротивления на рассматриваемом участке: – потери напора от местных сопротивлений. Для этого сложим все местные сопротивления на рассматриваемом участке: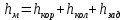 где, 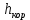 - потери напора на коробке всасывающей линии; - потери напора на коробке всасывающей линии;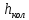 - потери напора на колене всасывающей линии; - потери напора на колене всасывающей линии;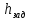 - потери напора на задвижке всасывающей линии. - потери напора на задвижке всасывающей линии.Используя формулу (13) получим: 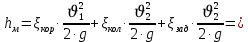 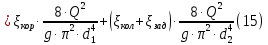 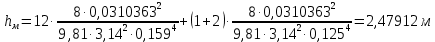 б) Теперь рассчитаем 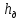 – потери напора по длине трубопровода. Они определяются как сумма потерь напора на участке трубопровода – потери напора по длине трубопровода. Они определяются как сумма потерь напора на участке трубопровода 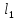 и потерь напора на участке трубопровода и потерь напора на участке трубопровода 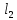 : :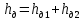 (16) (16)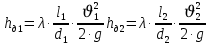 где 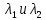 - коэффициенты гидравлического сопротивления 1 и 2 участков. - коэффициенты гидравлического сопротивления 1 и 2 участков.Для определения 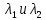 необходимо определить режим течения жидкости на соответствующих участках трубопровода. Для этого определимчисла необходимо определить режим течения жидкости на соответствующих участках трубопровода. Для этого определимчисла Рейнольдса для этих участков по формуле (12): 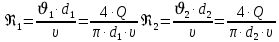 где 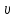 - кинематическая вязкость циркуляционной жидкости. - кинематическая вязкость циркуляционной жидкости.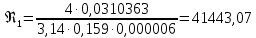 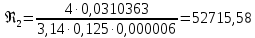 По полученным результатам вычисления чисел Rе определяем режим течения – турбулентный или ламинарный. Затем определим тип трубопровода (шероховатый или гладкий) на участках трубопровода 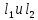 . Для этого находим значения величин обратной относительной шероховатости для обоих рассматриваемых участков по данным значениям dи . Для этого находим значения величин обратной относительной шероховатости для обоих рассматриваемых участков по данным значениям dи 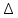 : :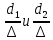 Оба участка принадлежат смешанным зонам труб, если их числа Rе принадлежат промежуткам: 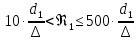 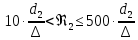 3180<41443,07  159000 1590002500<52715,58  125000 125000Оба числа Рейнольдса удовлетворяют условию. Для определения 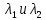 - воспользуемся формулой Альтшуля: - воспользуемся формулой Альтшуля: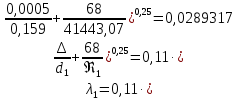 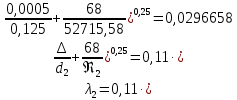 Теперь, когда известны все величины, можно найти суммарные потери напора на участках 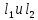 по формуле (16): по формуле (16):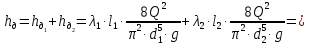 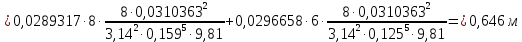 Подставив в формулу (14), получим: 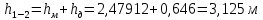 Найдем геометрическую высоту всасывания насоса 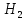 , воспользуемся формулой (4) из раздела 3.1: , воспользуемся формулой (4) из раздела 3.1: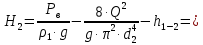 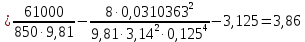 3.2Определение показания дифманометра скоростной трубки Для выполнения задания достаточно уравнения Бернулли для осевой трубки: 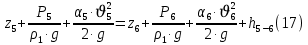 где 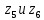 - расстояние от сечений 5-5 и 6-6соответственно до некоторой произвольно выбранной горизонтальной плоскости; - расстояние от сечений 5-5 и 6-6соответственно до некоторой произвольно выбранной горизонтальной плоскости;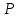 – давления в сечениях 5-5 и 6-6соответственно; – давления в сечениях 5-5 и 6-6соответственно;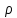 - плотность циркулирующей жидкости; - плотность циркулирующей жидкости;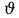 - скорость течения жидкости в сечении 5-5 и 6-6; - скорость течения жидкости в сечении 5-5 и 6-6;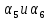 -коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях 5-5 и 6-6соответственно; -коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях 5-5 и 6-6соответственно;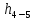 - потери напора на участках между выбранными сечениями; - потери напора на участках между выбранными сечениями;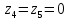 , если выбираем ось трубопровода за начало; , если выбираем ось трубопровода за начало;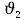 =0, так как жидкость внутри дифманометра почти неподвижна; =0, так как жидкость внутри дифманометра почти неподвижна;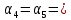 1. 1.В итоге имеем: 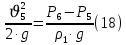 Из рисунка 1 видно разность давлений: 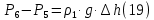 В результате уравнение (18) примет вид: 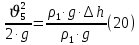 Имеем расчетную формулу для определения показания дифманометра: 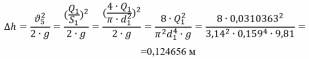 3.3 Построение эпюр скоростей Анализируя схему циркуляционной установки можно сделать вывод, что расход жидкости постоянный в любом сечении трубопровода. Следовательно, режим течения жидкости зависит от диаметра трубопровода нарассматриваемом участке. Это, в свою очередь, говорит об идентичности режима течения на участках трубопровода с одинаковыми диаметрами. В месте установки скоростной трубки режим течения идентичен режиму течения на участке трубопровода всасывающей линии. Следовательно, мы имеем турбулентный режим течения, который происходит в зоне сопротивления шероховатых труб. Формула для распределения скоростей в круглой трубе при турбулентном режиме в зоне шероховатых труб имеет следующий вид: 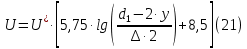 гдеU- местная скорость в данной точке сечения; 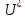 - динамическая скорость; - динамическая скорость;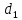 - диаметр трубопровода; - диаметр трубопровода;y- расстояние от оси трубопровода; 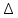 - эквивалентная шероховатость стенок труб; - эквивалентная шероховатость стенок труб;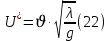 где, 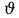 - средняя скорсоть течения жидкости; - средняя скорсоть течения жидкости;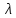 - коэффициент гидравлического сопротивления; - коэффициент гидравлического сопротивления;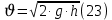 где h- показание дифманометра (или дифпьезометра) скоростной трубки. Подставив (22) и (23) в (21), получим: 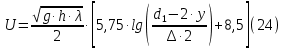 где − h показание дифманометра скоростной трубки. Для построения эпюры скоростей зададим значения у в интервале от 0 до 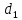 /2 с шагом 4,1 мм. Вычислим для каждого значения у местную скорость. Если количества полученных точек недостаточно для определения траектории кривой, то необходимо взять больше значений. По результатам составим таблицу и построим график. /2 с шагом 4,1 мм. Вычислим для каждого значения у местную скорость. Если количества полученных точек недостаточно для определения траектории кривой, то необходимо взять больше значений. По результатам составим таблицу и построим график.Вычислим значение местной скорости при y=4,1мм 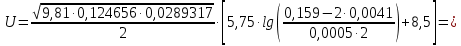 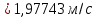 Таблица 2 – Таблица вычисленных местных скоростей
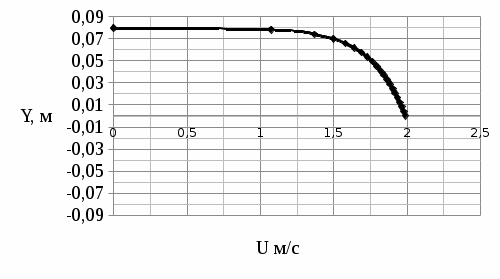 Рисунок 2 – Эпюра скоростей 3.5Определение установившегося уровня жидкости Для определения установившегося уровня жидкости в промежуточной емкости 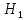 составим уравнение Бернулли для сечений 8-8 и 9-9 : составим уравнение Бернулли для сечений 8-8 и 9-9 :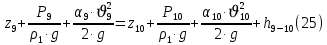 где 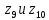 - расстояние от сечений 9-9и 10-10 соответственно до некоторой произвольно выбранной горизонтальной плоскости; - расстояние от сечений 9-9и 10-10 соответственно до некоторой произвольно выбранной горизонтальной плоскости;р - давления в сечениях 9-9и 10-10соответственно; 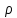 - плотность циркулирующей жидкости; - плотность циркулирующей жидкости;g - ускорение свободного падения; 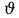 - скорость течения жидкости в сечениях 9-9и 10-10соответственно; - скорость течения жидкости в сечениях 9-9и 10-10соответственно;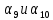 - коэффициенты Кориолиса, которые учитываютнеравномерность распределения скоростей в сечениях 9-9и 10-10 соответственно; - коэффициенты Кориолиса, которые учитываютнеравномерность распределения скоростей в сечениях 9-9и 10-10 соответственно;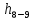 - потери напора на участках между выбранными сечениями. - потери напора на участках между выбранными сечениями.Плоскость сравнения совместим с сечением 2-2, тогда |
