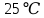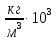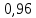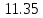№13 «Определение коэффициента вязкости жидкости». Отчет по лабораторной работе 13 Определение коэффициента вязкости жидкости
 Скачать 87.81 Kb. Скачать 87.81 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» Кафедра общей и технической физики Отчет по лабораторной работе №13 «Определение коэффициента вязкости жидкости» Выполнил: студент _____________ (подпись) Проверил: _____________ (подпись) Дата выполнения работы: Санкт-Петербург 2022 Цель работы Определить коэффициент вязкости жидкости методом Стокса. Краткое теоретическое содержание Процесс, изучаемый в работе В работе производится измерение вязкости жидкости по измерению скорости установившегося равномерного движения маленьких твердых шариков при их падении в исследуемой жидкости. Основные определения явлений, процессов, величин Вязкость (внутреннее трение) - есть свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одного слоя вещества относительно другого. Градиент скорости - отношение /у, характеризующее быстроту изменения скорости, где и у - разница в скорости и расстояние между соседними слоями соответственно. Равномерное прямолинейное движение – это движение, при котором за любые равные промежутки времени тело совершает равные перемещения. Скорость – это физическая векторная величина, равная отношению пути ко времени. Ускорение – это физическая величина, численно равная изменению скорости в единицу времени. Основные законы и соотношения, лежащие в основе вывода расчетных формул При движении плоских слоев сила трения между ними согласно закону Ньютона, Н:  где  - коэффициент пропорциональности, называемый коэффициентом вязкости или динамической вязкостью; S - площадь соприкосновения слоев; - коэффициент пропорциональности, называемый коэффициентом вязкости или динамической вязкостью; S - площадь соприкосновения слоев; 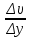 – градиент скорости. – градиент скорости.Выталкивающая сила по закону Архимеда для шарика, Н  Где 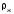 - плотность жидкости; - плотность жидкости;  – объём шарика; – объём шарика; – ускорение свободного падения; r- радиус шарика. – ускорение свободного падения; r- радиус шарика.Закон Стокса, Н  Где - коэффициент вязкости; r- радиус шарика; 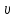 - скорость движения шарика; - скорость движения шарика;Второй закон Ньютона, Н  Где  – действующие на тело силы; m – масса тела; – действующие на тело силы; m – масса тела; 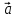 – ускорение, приобретаемое телом. – ускорение, приобретаемое телом.Схема экспериментальной установки 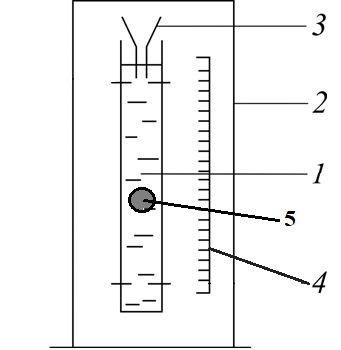 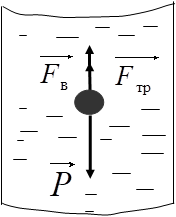 1 – Жидкость  Сила внутреннего трения Сила внутреннего трения 2 – Установка  Выталкивающая сила Выталкивающая сила3 – Воронка  Сила тяжести Сила тяжести4 – Линейка 5 – Шарик Основные расчетные формулы Сила внутреннего трения между слоями жидкости (закон Стокса), Н : 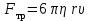 , ,где 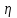 - коэффициент вязкости; r- радиус шарика; - коэффициент вязкости; r- радиус шарика; 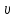 - скорость движения шарика; - скорость движения шарика;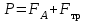 , ,где Р- сила тяжести; действующая на шарик; FА- сила Архимеда; Fтр- сила внутреннего трения; Сила тяжести, Н 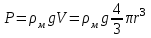 , ,где м - плотность материала шарика; V – объем шарика;  – ускорение свободного падения; r- радиус шарика; – ускорение свободного падения; r- радиус шарика;Выталкивающая сила, Н  , ,где 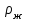 - плотность жидкости; - плотность жидкости;  – объём шарика; – объём шарика; – ускорение свободного падения; r- радиус шарика; – ускорение свободного падения; r- радиус шарика;Коэффициент вязкости жидкости, 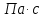  . .Где  – плотность материала шарика; – плотность материала шарика;  – плотность жидкости; – плотность жидкости; 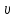 - скорость движения шарика; r- радиус шарика; - скорость движения шарика; r- радиус шарика;  – ускорение свободного падения; – ускорение свободного падения;Скорость, 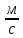 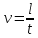 Где 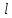 – расстояние, которое преодолел шарик; t – время. – расстояние, которое преодолел шарик; t – время.Радиус, м  Где d – диаметр шарика. Формулы для расчёта погрешности косвенных измерений 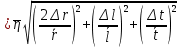 где 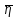 - среднее значение коэффициента вязкости, - среднее значение коэффициента вязкости,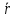 – среднее значение радиуса шарика, – среднее значение радиуса шарика,  – среднее значение пройденного пути, – среднее значение пройденного пути, 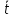 – среднее значение времени. – среднее значение времени.Таблицы «Технические данные прибора» Таблица 1
«Результаты измерений» Таблица 2
Исходные данные:  ; ; 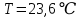 ; ; 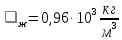 ; ;  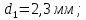 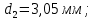     Погрешности прямых измерений:  = 0,02 м = 0,02 м  = 1 с = 1 с   Вычисления Пример вычислений для таблицы 2, опыта 1: Радиус, м:  Скорость, 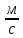 : : 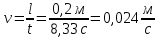 Коэффициент вязкости, 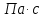 : :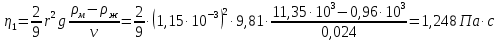 Вычисляем погрешность косвенных измерений  : :Среднее значение коэффициента вязкости 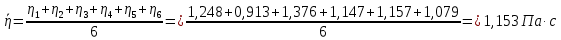 Среднее значение радиуса шарика 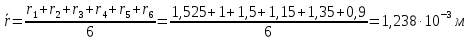 Среднее значение времени  Погрешность косвенных измерений 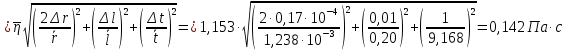 Результаты Вывод: В данной работе экспериментально был определен коэффициент вязкости жидкости. Получили:  ; ;Путем постановки 6 опытов со стальными и свинцовыми шариками, удалось установить, что скорость шарика, движущегося в сосуде с жидкостью, зависит от размеров и плотности шарика. Полученные результаты имеют небольшую погрешность, что позволяет говорить о точности расчетной формулы и о незначительных погрешностях при измерениях и вычислениях. Коэффициент вязкости при  равен равен 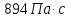 . В среднем . В среднем 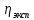 больше больше  на 28% (опыт №1: на 28% (опыт №1: 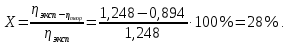 |