Лабораторная работа-m12-2. Лабораторная работа m1 Определение ускорения свободного падения на широте города Владивостока Выполнил студент соис18
 Скачать 44.25 Kb. Скачать 44.25 Kb.
|
|
Министерство образования и науки РФ ВЛАДИВОСТОКСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЭКОНОМИКИ И СЕРВИСА АКАДЕМИЧЕСКИЙ КОЛЛЕДЖ ВГУЭС ЛАБОРАТОРНАЯ РАБОТА M-1 Определение ускорения свободного падения на широте города Владивостока Выполнил студент СО-ИС-18 Мазур Денис Олегович__________ Проверил Доценко Б.А.__________ Владивосток 2018 ЦЕЛЬ РАБОТЫ: Рассчитать ускорение свободного падения с помощью маятника. Оценить погрешность измерения. Выяснить зависимость ускорения свободного падения g от уровня высоты h. ОБОРУДОВАНИЕ: линейка, секундомер, металлический шарик, нить. Теоретическая часть Ускорение свободного падения Ускорение свободного падения – это ускорение, придаваемое любому телу силой тяжести, которая складывается из гравитационного притяжения планеты (или другого астрономического тела) и центробежных сил, вызванных её вращением. Это ускорение зависит от географической широты местности, высоты над уровнем моря h, плотности земных пород и ряда других факторов. Поскольку Земля является не точным шаром, а эллипсоидом, несколько сплюснутым у полюсов, и, кроме того, на тела действуют центробежные силы, особенно заметные на экваторе, то величина g зависит от географической широты и на полюсе несколько больше, чем на экваторе. Справочные данные:
Математический маятник Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке, и совершающую под действием силы тяжести гармонические колебания в вертикальной плоскости. Как известно, период малых колебаний математического маятника выражается формулой: Т = 2π√ где g – ускорение свободного падения (м/с²); π = 3,14; l = длина нити (м); N – число колебаний за время t, измеренное с помощью секундомера. Из последней формулы видно, что для определения ускорения свободного падения необходимо знать длину маятника и период его колебаний. Длину маятника можно измерить непосредственно с помощью линейки, а период колебаний можно определить по формуле Тср. = Тогда для определения ускорения свободного падения получим следующую формулу: gср. = Расчетная формула: g= 4π 2n2l t2 Экспериментальная часть
1. Измерить длину маятника, то есть расстояние от точки подвеса до центра шарика. Записать полученный результат в таблицу №1 «Измерение на 1 уровне». 2. Отклонить маятник от положения равновесия, аккуратно отпустить, запустить секундомер и засечь время 10 полных колебаний. Результаты внести в таблицу №1. 3. Вычислить ускорение свободного падения по формуле g= 4π 2n2l t2 4. Рассчитать относительную и абсолютную погрешности ускорения свободного падения. Записать результат в таблицу№1. Расчетные формулы: ∆ g= 4,3* 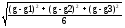 Относительная погрешность ﻉ=(∆ g/ g)100% 5. Изменить длину маятника и повторить эксперимент в той же последовательности. Все измерения занести в таблицу№1. 6. Повторить эксперимент на 2 уровне и записать полученные результаты в таблицу №2.
Таб.1 g1= 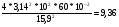 g2= 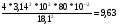 g3= 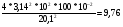 ∆ g= 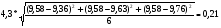 ﻉ= 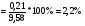 Таб.2 g1=  g2= 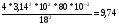 g3= 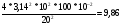 ∆ g=  ﻉ= 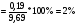 Чем больше длина нити, тем меньше относительная ошибка, допущенная при измерении длины маятника. Чем больше длина нити по сравнению с диаметром шарика, тем точнее его можно принять за математический маятник. Следовательно, в данной работе длину маятника надо брать по возможности большой. При малых углах отклонений период колебания математического маятника пропорционален квадратному корню из длины маятника, обратно пропорционален квадратному корню из ускорения свободного падения и не зависит от амплитуды колебаний и массы маятника. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
