Изобр. схем. Изображение схем релейной защиты на чертежах
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
|
Изображение схем релейной защиты на чертежах. Условные обозначения. Для изображения на чертежах схем релейной защиты применяются специальные условные обозначения электрических машин, аппаратов, реле, приборов и др. Рис.1. 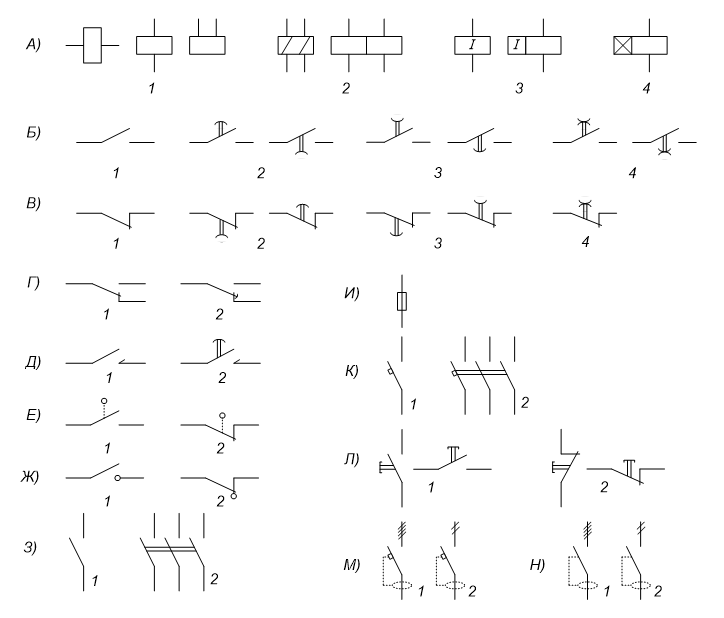 Рис.1. А) – обмотки реле, контакторов: 1 – однообмоточных; 2 – двухобмоточных; 3 – реле тока; 4 – реле времени. Б) – контакты реле замыкающие: 1 – без замедления; 2 – с замедлением на замыкания; 3 – с замедлением на размыкание; 4 – с замедлением на замыкание и размыкание. В) – контакты реле размыкающие: 1 – без замедления; 2 – с замедлением на размыкание; 3 – с замедлением на замыкание; 4 – с замедлением на замыкание и размыкание. Г) – контакты реле переключающие: 1 – с размыканием цепи; 2 – без размыкания цепи. Д) – контакты реле замыкающие кратковременно (импульсные): 1 – быстродействующий; 2 – с замедлением. Е) – контакты путевого выключателя: 1 – замыкающий; 2 – размыкающий (используется для обозначения вспомогательных контактов на приводах выключателей, разъединителей). Ж) – контакты без самовозврата (указательных реле): 1 – замыкающий; 2 – размыкающий. З) – рубильник: 1 – однофазный; 2 – трехфазный. И) – предохранитель К) – автоматический выключатель: 1 – однофазный; 2 – трехфазный. Л) – кнопки: 1 – замыкающие; 2 – размыкающие. М) – дифавтомат: 1 – трехфазный; 2 – однофазный. М) – УЗО: 1 – трехфазное; 2 – однофазное. Условные обозначения периодически пересматриваются и вводятся для обязательного применения государственным стандартом (ГОСТ). В разной литературе или схемах изданные в разное время условные обозначения одних и тех же элементов могут отличатся. Все аппараты на схемах изображаются в положениях, соответствующих отсутствию напряжения во всех цепях. Изображение схем релейной защиты на чертежах. В зависимости от назначения применяются три основных вида схем релейной защиты: принципиальные, монтажные и структурные. Принципиальные схемы релейной защиты и цепей управления выключателями выполняются по отдельным цепям: тока, напряжения, оперативного тока, сигнализации и т.д. В этих схемах реле и другие аппараты изображаются в расчленённом виде, т.е. обмотки реле изображаются в одной части схемы, контакты – в другой и т.д. Схемы внутренних соединений реле, их зажимы и источники оперативного тока на принципиальных схемах не показываются. Сложные схемы поясняются надписями, указывающими назначение отдельных цепей. Пример. 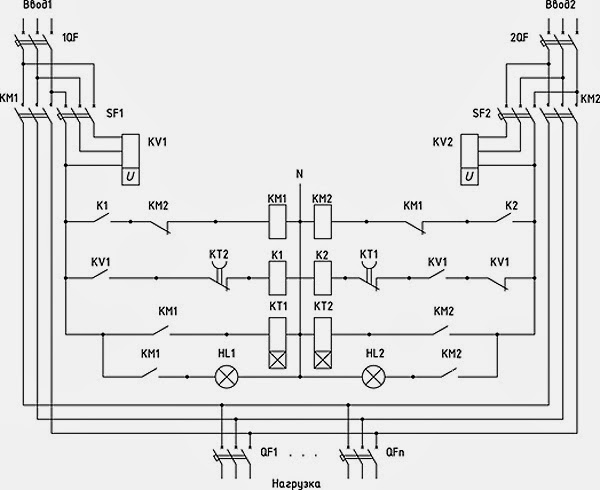 Монтажные схемы представляют собой рабочие чертежи, по которым производится монтаж панелей релейной защиты, автоматики, управления, сигнализации и др. На монтажных схемах реле, приборы, зажимы и соединяющие их провода располагаются, как на панели, и маркируются. Монтажные схемы, на которых отражены все фактические соединения, выполненные при монтаже и наладке, называются исполнительными. Пример. 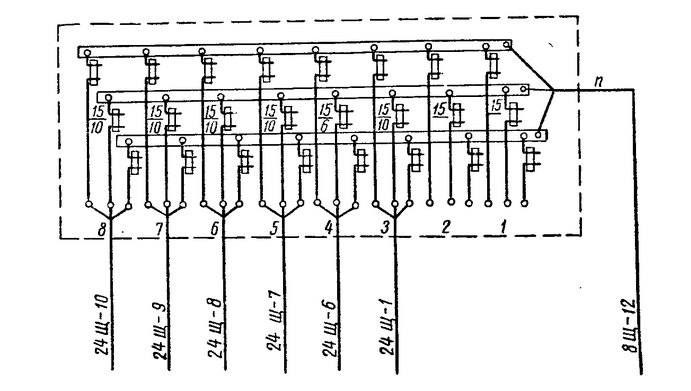 Структурные схемы применяются для изображения общей структуры устройств релейной защиты и автоматики без выделения отдельных реле и других аппаратов. Они изображаются не с помощью приведенных выше условных обозначений, а в виде целых узлов или органов устройства и взаимных связей между ними. Узлы и органы обычно изображаются прямоугольниками, в которые помещаются надписи или условные индексы, поясняющие назначение данного узла или органа. Для изображения структурных схем используются также условные обозначения логических элементов. Пример. 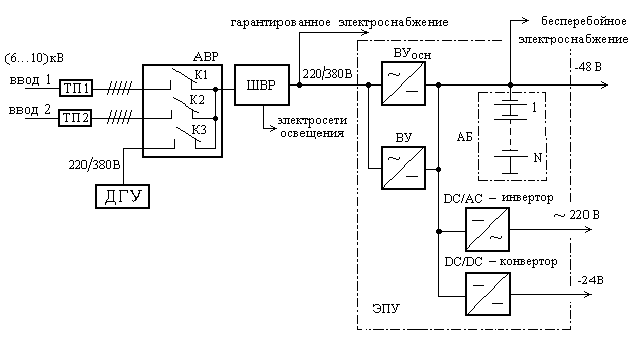 Векторные диаграммы при наличии трансформации. Векторные диаграммы при наличии трансформации. При наличии в электрической цепи трансформаторов необходимо ввести дополнительные условия, для того чтобы сопоставлять векторные диаграммы токов и напряжений на разных сторонах трансформатора. Положительные направления токов при этом следует задавать с учетом полярности обмоток трансформатора. В зависимости от направления намотки обмоток трансформатора взаимное направление токов в них меняется. Для того чтобы определять направление токов в обмотках силового трансформатора и сопоставлять их между собой, обмоткам трансформатора дают условные обозначения «начало» и «конец». В схеме, приведенной на рис.1.6, между источником ЭДС и нагрузкой включим трансформатор (рис.1.12, а). Обозначим начала обмоток силового трансформатора буквами А и а, концы – Х и х. При этом следует иметь в виду, что начало одной из обмоток принимается произвольно, а второй – определяется на основании условных положительных направлений токов, заданных для обеих обмоток трансформатора. 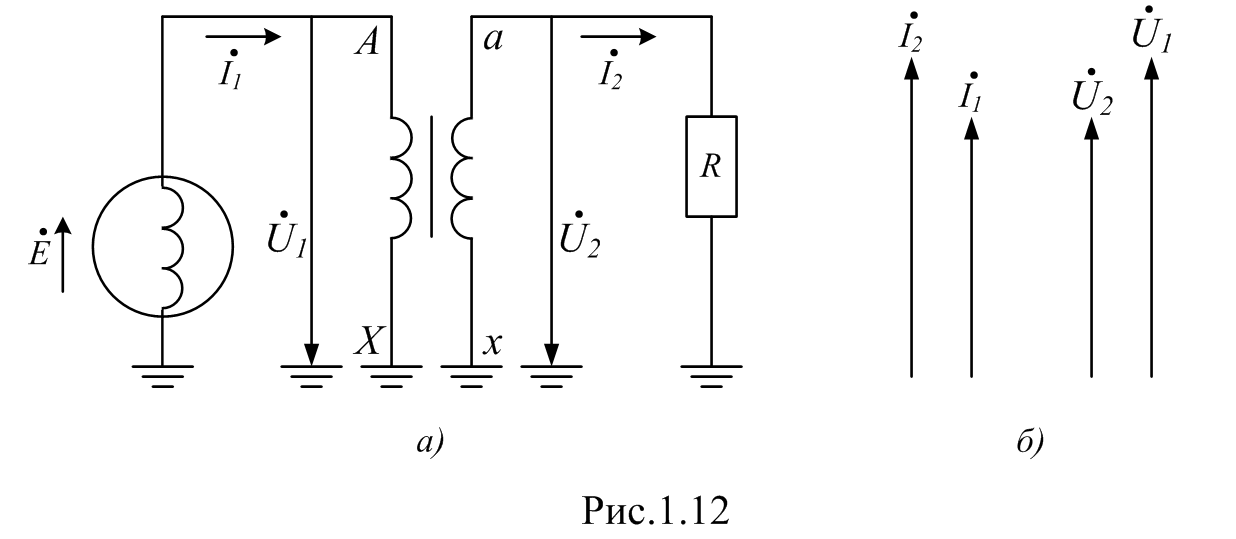 На рис.1.12, а показаны положительные направления токов в обмотках силовых трансформаторов. В первичной обмотке положительным считается направление тока от начала к концу, а во вторичной – от конца к началу. При таких условно принятых положительных направлениях токов в обмотках трансформатора направление тока в нагрузке остается таким же, каким оно было бы при отсутствии трансформатора и непосредственном подключении нагрузки к генератору (см. рис.1.6 и 1.12). При этом, поскольку магнитные потоки, создаваемые в магнитопроводе трансформатора обоими токами (первичным и вторичным), направлены встречно (рис.1.13), для идеального трансформатора, пренебрегая током намагничивания, можно записать следующее равенство:  или  где  – магнитные потоки в магнитопроводе трансформатора, а – магнитные потоки в магнитопроводе трансформатора, а 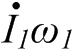 и и 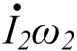 – магнитодвижущие силы (МДС), создающие эти потоки. – магнитодвижущие силы (МДС), создающие эти потоки.Из последнего уравнения: 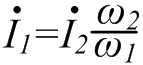 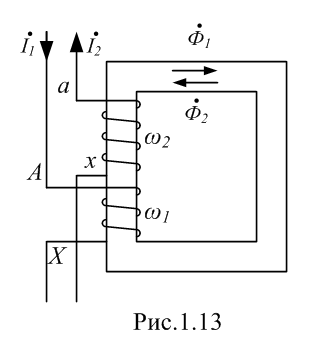 Согласно последнему равенству векторы В рассматриваемом случае имеет место соединение обмоток трансформатора по схеме 1/1-12. Соответственно для трехфазного трансформатора Y/Y-12 схема соединений и векторная диаграмма токов и напряжений показаны на рис.1.14. 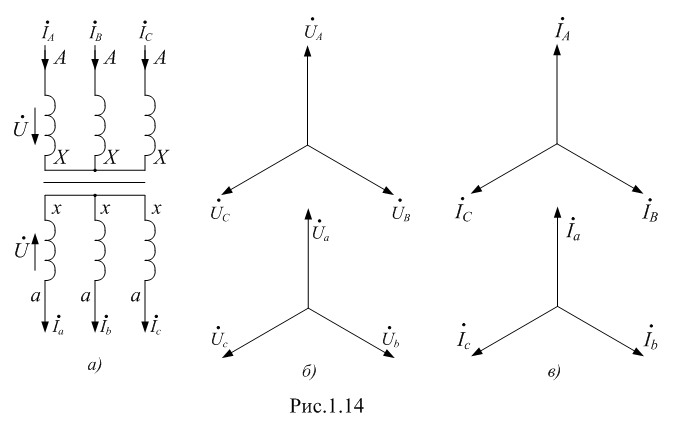 На рис.1.15, б построены векторные диаграммы напряжений, соответствующие схеме соединения трансформатора Y/Δ-11. На стороне высшего напряжения, где обмотки соединены в звезду, междуфазные напряжения в √3 раз превышают фазные напряжения. На стороне же низшего напряжения, где обмотки соединены в треугольник, междуфазные и фазные напряжения равны. Векторы междуфазных напряжений стороны низшего напряжения опережают на 30о аналогичные векторы междуфазных напряжений стороны высшего напряжения, что и соответствует схеме соединений Y/Δ-11. 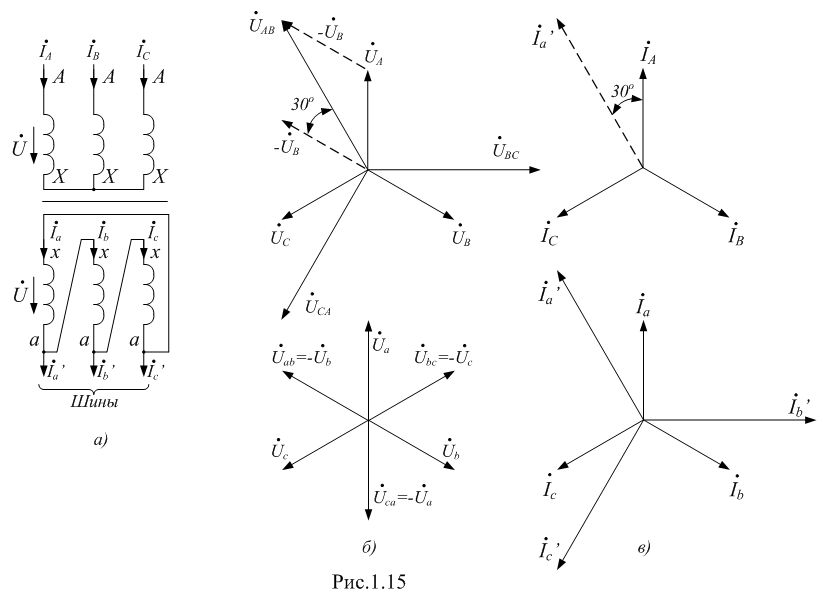 Для рассматриваемой схемы соединений обмоток трансформатора можно построить и векторные диаграммы токов, проходящих с обеих его сторон. При этом следует иметь в виду, что на основании принятых нами условий определяются только положительные направления токов в обмотках трансформатора. Положительные же направления токов в линейных проводах, соединяющих выводы обмоток низшего напряжения трансформатора с шинами, могут быть приняты произвольно независимо от положительных направлений токов, проходящих в треугольнике. Так, например, если принять положительные направления токов в фазах на стороне низшего напряжения от выводов, соединенных в треугольник, к шинам (рис.1.15, а), можно записать следующие равенства: 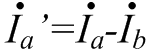 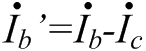 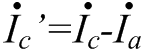 Соответствующая векторная диаграмма токов показана на рис.1.15, в. Аналогично можно построить векторную диаграмму токов и для случая, когда положительные направления токов приняты от шин к выводам треугольника (рис.1.16, а). Этому случаю соответствует следующие равенства: 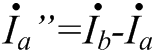 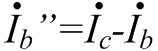 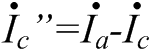 и векторные диаграммы, приведенные на рис.1.16, б. 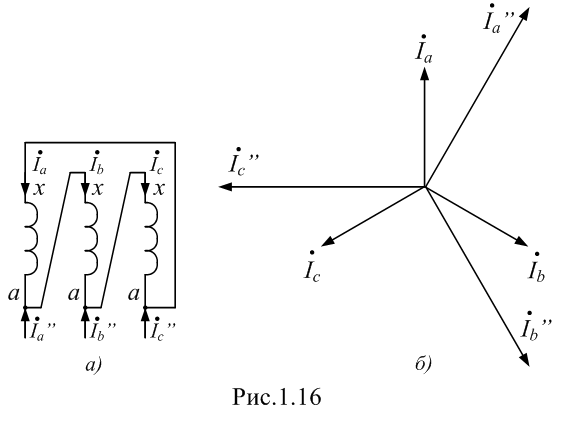 Сравнивая диаграммы токов, приведенные рис.1.15, в и 1.16, б, можно сделать вывод, что векторы фазных токов, проходящих в проводах, соединяющих выводы обмоток низшего напряжения трансформатора и шины, находятся в противофазе. Конечно, как те, так и другие диаграммы верны. Таким образом, при наличии в схеме обмоток, соединенных в треугольник, необходимо задаваться положительными направлениями токов как в самых обмотках, так и в линейных проводах, соединяющих треугольник с шинами. В рассматриваемом случае при определении группы соединений силового трансформатора удобно за положительные принимать направления от выводов низшего напряжения к шинам, так как при этом векторные диаграммы токов совпадают с принятым обозначением групп соединения силовых трансформаторов (см.рис.1.15, б и в). Аналогично могут быть построены векторные диаграммы токов и для других групп соединения силовых трансформаторов. Сформулированные выше правила построения векторных диаграмм токов и напряжений в схемах с трансформаторами действительны и для измерительных трансформаторов тока и напряжения. Вопросы для самопроверки: Что следует учитывать при добавлении трансформатора в цепь, чтобы сопоставлять векторные диаграммы токов и напряжений на разных сторонах трансформатора? Чем отличаются векторные диаграммы трансформаторов Y/Y-12 и Y/Δ-11? Векторные диаграммы Понятие о векторах. На рис.1.4 приведена кривая изменения переменного тока во времени. Ток сначала растет от нуля (при φ=0º) до максимального положительного значения + Imax (при φ=90о), затем убывает, переходит через нуль (при φ=180о), достигает максимального отрицательного значения – Imax (при φ=270о) и, наконец, возвращается к нулю (при φ=360о). после этого цикл изменения тока повторяется. Кривая изменения переменного тока во времени, приведенная на рис.1.4, называется синусоидой. Время Т, в течение которого происходит полный цикл изменения тока, соответствующий изменению угла на 360о, называется периодом переменного тока. Число периодов за 1 секунду называется частотой переменного тока. В промышленных установках и в быту в на территории бывшего СССР и в других странах Европы используется главным образом переменный ток частотой 50 Гц. Этот ток 50 раз в секунду принимает положительное и отрицательное направление. Изменение переменного тока во времени можно записать в следующем виде. Где i – мгновенное значение тока, т.е. значение тока в каждый момент времени; Imax – максимальное значение тока; ω=2πf – угловая частота переменного тока, f=50 Гц, ω=2π·50=314; α – начальный угол, соответствующий моменту времени, с которого начинается отсчет времени (при t=0). Для частного случая, показанного на рис.1.4, α=0о. Анализируя действие устройств релейной защиты и автоматики, необходимо сопоставлять токи и напряжения, складывать или вычитать их, определять углы между ними и производить другие операции. Пользоваться при этом кривыми, подобными приведенной на рис.1.4, неудобно, поскольку построение синусоид тока и напряжения занимает много времени и не дает простого и наглядного результата. Поэтому для упрощения принято изображать токи и напряжения в виде отрезков прямых линий, имеющих определенную длину и направление, - так называемых векторов (А0 на рис.1.4). один конец вектора закреплен на точке 0 – начало координат, а второй вращается против часовой стрелки. 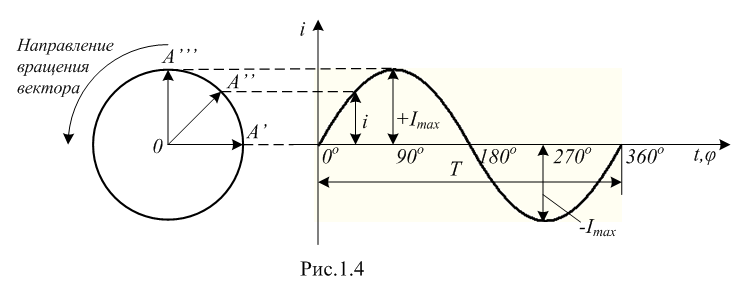 Мгновенное значение тока или напряжения в каждый момент времени определяется проекцией на вертикальную ось вектора, длина которого равна максимальному значению тока или напряжения. Эта проекция будет становится то положительной, то отрицательной, принимая максимальные значения при вертикальном расположении вектора. За время Т, равное периоду переменного тока, вектор совершит полный оборот по окружности (360о), занимая последовательно положения 0А’,0A”, 0A’’’ и т.д. При частоте переменного тока 50 Гц вектор будет совершать 50 об/с. Таким образом, вектор тока или напряжения – это отрезок прямой, равный по величине максимальному значению тока или напряжения, вращающийся относительно точки 0 против движения часовой стрелки со скоростью, определяемой частотой переменного тока. Зная положение вектора в каждый момент времени, можно определить мгновенное значение тока или напряжения в данный момент. Так, для положения вектора тока 0А, показанного на рис.1.5, его мгновенное значение определяется проекцией на вертикальную ось, т.е. 0А”=0А sin φ. 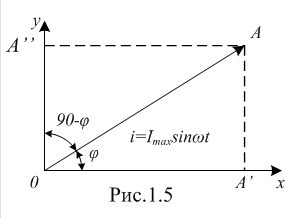 На основании рис.1.5 можно также сказать, что ток в данный момент времени имеет положительное значение. Однако это ещё не дает полного представления о протекании процесса в цепи переменного тока, так как неизвестно, что значит положительный или отрицательный ток, положительное или отрицательное напряжение. Для того чтобы векторные диаграммы токов и напряжений давали полную картину, их нужно увязать с фактическим протеканием процесса в цепи переменного тока, т.е. необходимо предварительно принять условные положительные направления токов и напряжений в рассматриваемой схеме. Без выполнения этого условия, если не заданы положительные направления токов и напряжений, любая векторная диаграмма не имеет никакого смысла. Рассмотрим простую однофазную цепь переменного тока, приведенную на рис.1.6, а. От однофазного генератора энергия предается в активное сопротивление нагрузкиR. Зададимся положительными направлениями токов и напряжений в рассматриваемой цепи. За условное положительное направление напряжения и ЭДС примем направление, когда потенциал вывода генератора или нагрузки, связанного с линией, выше потенциала вывода, соединенного с землей. В соответствии с правилами, принятыми в электротехнике, положительное направление для ЭДС обозначено стрелкой, направленной в сторону более высокого потенциала (от земли к линейному выводу), а для напряжения – стрелкой, направленной в сторону более низкого потенциала (от линейного вывода к земле). 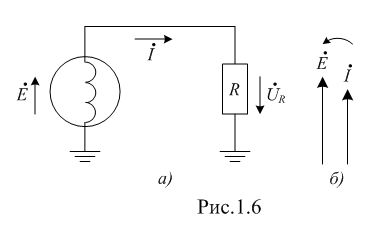 Переменный ток будет считать положительным, когда во внешней цепи он проходит от шин генератора к нагрузке (обозначено стрелкой). Построим векторы ЭДС и тока, характеризующие работу рассматриваемой цепи (рис.1.6, б). Вектор ЭДС произвольно обозначим вертикальной линией со стрелкой, направленной вверх. Для построения вектора тока запишем для цепи уравнение согласно второму закону Кирхгофа: отсюда 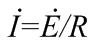 Поскольку знаки векторов тока и ЭДС в выражении совпадают, вектор тока будет совпадать с вектором ЭДС и на рис.1.6, б. Здесь и в дальнейшем при построении векторов будем откладывать их по величине равным эффективному значению тока и напряжения, что удобно для выполнения различных математических операций с векторами. Как известно, эффективные значения тока и напряжений в √2 раз меньше соответствующих максимальных (амплитудных). При заданных положительных направлениях тока и напряжения однозначно определяется и знак мощности. Положительной в рассматриваемом случае будем считать мощность, направленная от шин генератора в линию: так как векторы тока и ЭДС на рис.1.6, б совпадают. Аналогичные соображения могут быть высказаны и для трехфазной цепи переменного тока, показанной на рис.1.7, а. В этом случае во всех фазах приняты одинаковые положительные направления, чему соответствует симметричная диаграмма токов и напряжений, приведенная на рис.1.7, б. Отметим, что симметричной называется такая трехфазная система векторов, когда все три вектора равны по величине и сдвинуты относительно друг друга на угол 120о. 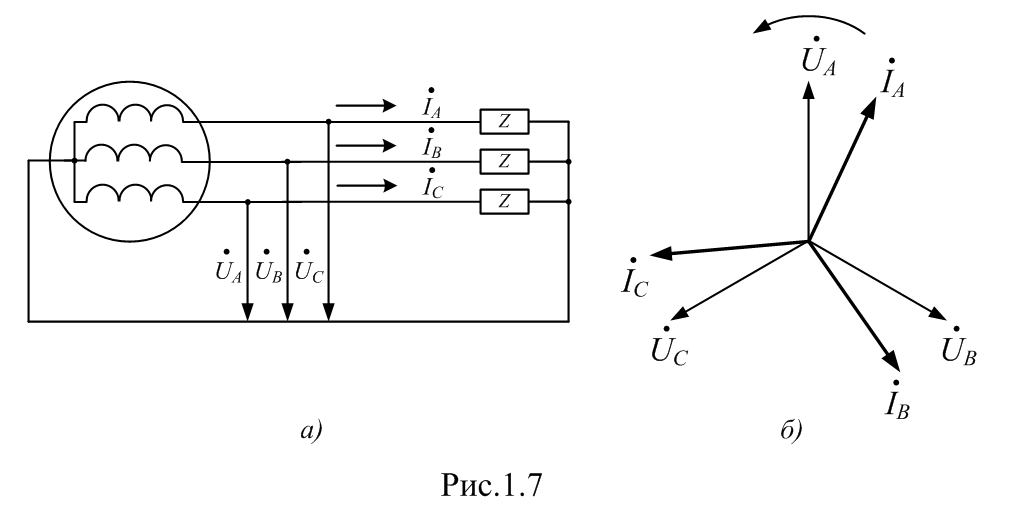 Операции с векторами. Когда мы рассматриваем только одну кривую тока или напряжения, начальное значение угла, с которого начинается отсчет, или, иначе говоря, положение вектора на диаграмме, соответствующее начальному моменту времени, может быть принято произвольным. Если же одновременно рассматриваются два или несколько токов и напряжений, то, задавшись начальным положением на диаграмме одного из векторов, мы тем самым уже определяем положение всех других векторов. Все три вектора фазных напряжений: Сложение векторов производится геометрическим суммированием по правилу параллелограмма, как показано на рис.1.8, а, на котором построена сумма токов ( 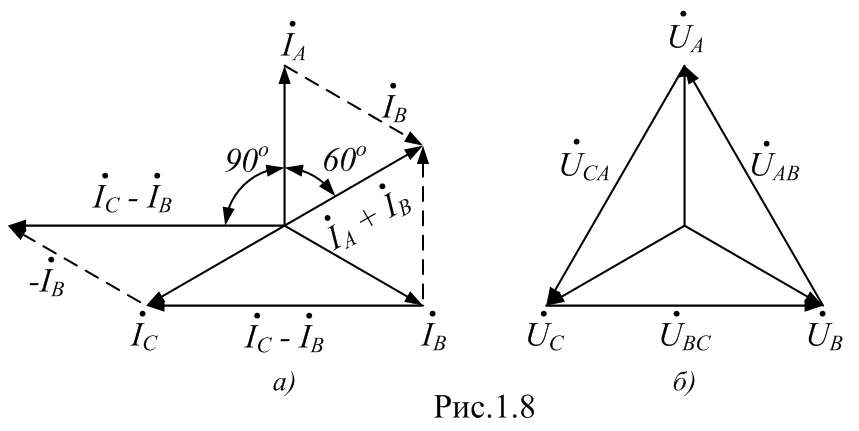 Аналогично строится векторная диаграмма межфазных напряжений, например, 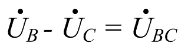 (рис.1.8, б). (рис.1.8, б).Очевидно, что положение вектора на плоскости определяется его проекциями на две любые оси. Так, например, для того чтобы определить положение вектора 0А(рис.1.9), достаточно знать его проекции на взаимно перпендикулярные оси: 0A’= 0A cos φ; 0A’’= 0A sin φ = 0A cos (90o – φ). Отложим на осях координат проекции векторов 0А’ и 0А’’ и восстановим из точек А’ и A’’ перпендикуляры к осям. Точка пересечения этих перпендикуляров и есть точка А – один конец вектора, вторым концов которого является точка 0 – начало координат. 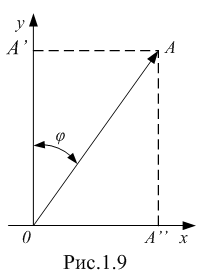 Назначение векторных диаграмм. Работникам, занимающимся проектированием и эксплуатацией релейной защиты, часто приходится использовать в своей работе так называемые векторные диаграммы – векторы токов и напряжений, построенные на плоскости в определенном сочетании, соответствующем электрическим процессам, происходящим в рассматриваемой схеме. Анализ векторных диаграмм токов и напряжений является одним из важных, а в ряде случаев единственным способом проверки правильности соединения цепей тока и напряжения и включения реле в схемах дифференциальных и направленных защит. По сути построение векторной диаграммы целесообразно во всех случаях, когда к рассматриваемому реле подаются две или более электрические величины: разность токов в максимальной токовой или дифференциальной защите, ток и напряжение в реле направления мощности или в направленном реле сопротивления. Векторная диаграмма позволяет сделать заключение о том, как рассматриваемая защита будет работать при КЗ, т.е. оценить правильность ее включения. Взаимное расположение векторов токов и напряжений на диаграмме определяется характеристикой рассматриваемой цепи, а также условно принятыми положительными направлениями токов и напряжений. Для примера рассмотрим две векторные диаграммы. На рис.1.10 показана однофазная цепь переменного тока, состоящая из генератора и последовательно соединенных емкостного, активного и индуктивного сопротивлений (примем при этом, что индуктивное сопротивление больше емкостного ХL > XC). Положительные направления токов и напряжений, так же как и в случаях, рассмотренных выше, обозначены на рис.1.10, а стрелками. 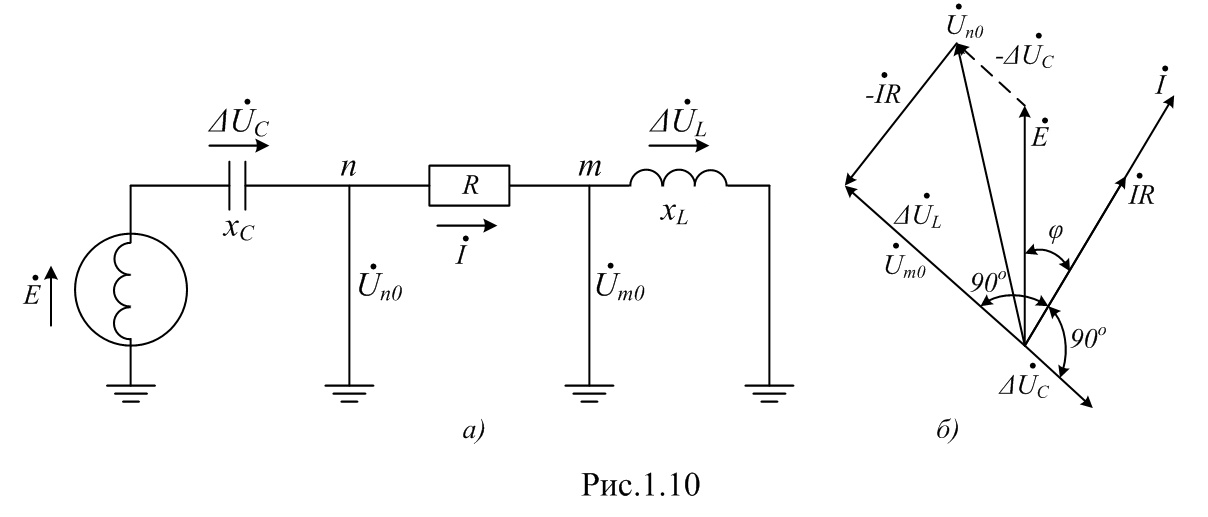 Построение векторной диаграммы начнем с вектора ЭДС Е, который расположим на рис.1.10, б вертикально. Ток, проходящий в рассматриваемой цепи, определится из следующего выражения: 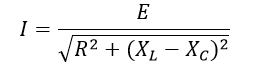 Поскольку в рассматриваемой цепи имеются активные и реактивные сопротивления, причем ХL > XC, вектор тока отстает от вектора напряжения на угол φ: 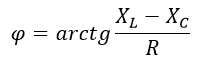 Напряжение в точке n на рис.1.10, а определится согласно следующему выражению: 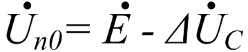 На рис.1.10, б построен вектор 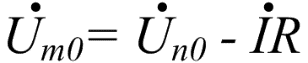 Как видно из рис.1.10, б, этот последний вектор Рассмотрим другую цепь переменного тока, приведенную на рис.1.11, а, и построим векторную диаграмму, характеризирующую распределение токов в параллельных ветвях. Для построения диаграммы примем, что активное и емкостное сопротивление равны R=XC. 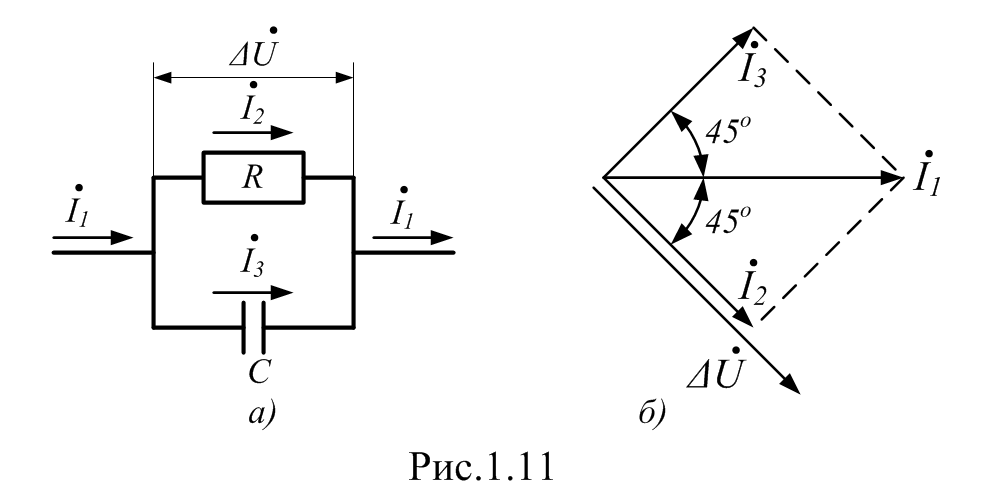 Построение векторной диаграммы начнем с вектора 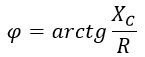 В рассматриваемом случае φ=45о. Вектор тока Вопросы для самопроверки: Что такое вектор? Зачем нужны векторные диаграммы? Что такое частота переменного тока? Что означает, когда говорят, что один вектор «опережает» или «отстает» от другого вектора? Как производится сложение и вычитание векторов? |
