ИЗУЧЕНИЕ КИНЕМАТИКИ И ДИНАМИКИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ НА МАШИНЕ АТВУДА. Физика лаба 1.1 - Литвинов. изучение кинематики и динамики поступательного движения на машине атвуда
 Скачать 86.8 Kb. Скачать 86.8 Kb.
|
|
ОТЧЁТ о лабораторной работе № 1.1 «ИЗУЧЕНИЕ КИНЕМАТИКИ И ДИНАМИКИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ НА МАШИНЕ АТВУДА» Студента группы: ИНБ-б-о-21-1 Литвинова Егора Романовича Цель работы: изучение кинематики и динамики поступательного движения. Измерительные приборы и их характеристики
Принадлежности и материалы: тетрадь, карандаш, грузики (m=10г, 20г, 30г, 40г) Краткая теория. При поступательном движении все точки тела движутся одинаково, и его движение задается и изучается так же, как движение одной точки. Основными кинематическими характеристиками движущейся точки являются скорость и ускорение, которые определяются по законам динамики. Массы грузов одинаковы (М1 = М2 = М), поэтому для того, чтобы вывести систему из равновесия, на груз 2 кладут перегрузок 5 массой m. На каждый груз действуют две силы: сила тяжести Mg или (M + m)g и сила реакции нити T1 или T2. Под действием этих сил грузы будут двигаться поступательно в противоположных направлениях. Ускорение грузов а может быть определено из второго закона Ньютона который можно записать для первого груза в виде: А для второго груза: Если пренебречь силами трения, а также массами нити и блока, то силы реакции нити T1 и T2 равны по величине: T1 = T2 = T. С учетом этих упрощений запишем уравнения (1) и (2) в проекциях на вертикальную ось: 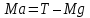 (3) (3)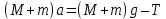 Исключив из системы (3) силу реакции Т, получим:  (4) (4)В случае равноускоренного движения скорость грузов v и перемещение h, грузов за время t определяются уравнениями 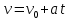  Так как начальная скорость v0 = 0, то 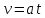 (5) (5)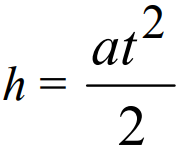 (6) (6)Соотношение (6) можно проверить экспериментально, сняв зависимость h от t. Зависимость h(t), как следует из (6), нелинейная. Поэтому для удобства экспериментальной проверки эту зависимость следует линеаризовать. Используя график линеаризованной зависимости h = f1(t2), можно определить величину ускорения а через угловой коэффициент прямой.  (7) (7)Соотношение (4) также может быть проверено экспериментально. Если брать перегрузки массой m << M, то 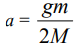 (8) (8)т.е. зависимость a = f2(m) должна быть линейной. Схема установки. 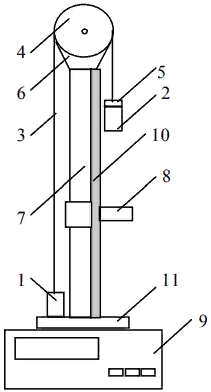 1,2 – грузы 1,2 – грузы3 – нить 4 – легкий блок 5 – кольцевой перегрузок 6 – верхний кронштейн 7 – стойка 8 – фотодатчик 9 – электронный миллисекундомер 10 – линейка 11– нижний кронштейн Таблицы измерений
Расчет измеряемых величин. 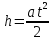 ⇒ ⇒ 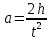 Оценка погрешностей: 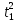 Найдём среднеарифметическое значение отдельных измерений по формуле 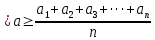 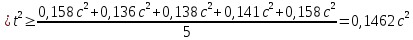 Точность соответствия среднего значения истинному зависит от ряда факторов, в первую очередь – от точности каждого отдельного измерения и от числа этих измерений. Укажем интервал значений измеряемой величины a = ± ∆a, в пределах которого с определенной вероятностью может оказаться истинное значение измеряемой величины.  Рассчитаем отклонения от среднеарифметического каждого значения измеряемой величины: 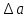 1= 1= 1; 1;  =0,1462- 0,158 = -0,0118c2 =0,1462- 0,158 = -0,0118c2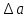 2= 2= 2; 2; 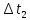 = 0,1462 – 0,136 = 0,0102c2 = 0,1462 – 0,136 = 0,0102c2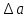 3= 3= 3; 3; 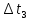 = 0,1462 – 0,138 = 0,0082c2 = 0,1462 – 0,138 = 0,0082c2. . . 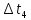 = 0,1462 – 0,141 = 0,0052c2 = 0,1462 – 0,141 = 0,0052c2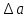 n= n= n n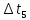 = 0,1462 – 0,158 = -0,0118c2 = 0,1462 – 0,158 = -0,0118c2Рассчитать среднеквадратичную погрешность результатов измерений 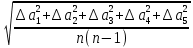 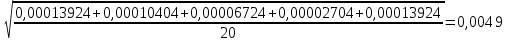 с сРассчитать полуширину доверительного интервала по формуле: 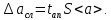 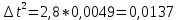 c2 c22) 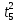 Найдём среднеарифметическое значение отдельных измерений по формуле 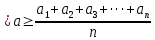  Точность соответствия среднего значения истинному зависит от ряда факторов, в первую очередь – от точности каждого отдельного измерения и от числа этих измерений. Укажем интервал значений измеряемой величины a = ± ∆a, в пределах которого с определенной вероятностью может оказаться истинное значение измеряемой величины.  Рассчитаем отклонения от среднеарифметического каждого значения измеряемой величины: 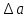 1= 1= 1; 1;  = 0,7474-0,743 = 0,0044c2 = 0,7474-0,743 = 0,0044c2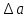 2= 2= 2; 2; 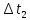 = 0,7474– 0,746 = 0,0014c2 = 0,7474– 0,746 = 0,0014c2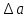 3= 3= 3; 3; 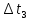 = 0,7474– 0,745= 0,0024c2 = 0,7474– 0,745= 0,0024c2. . . 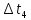 = 0,7474– 0,748 = −0,0006c2 = 0,7474– 0,748 = −0,0006c2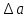 n= n= n n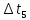 = 0,7474– 0,755 = −0,0076c2 = 0,7474– 0,755 = −0,0076c2Рассчитать среднеквадратичную погрешность результатов измерений 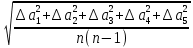 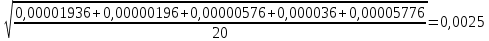 c cРассчитать полуширину доверительного интервала по формуле: 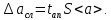 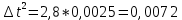 c2 c2Вывод: в процессе проведения лабораторной работы изучил кинематику и динамику поступательного движения. График экспериментальной зависимости h = f1(t 2 ) оказался прямой линией (в пределах погрешности измерений), проходящей через начало координат, следовательно зависимость (6) подтверждена экспериментально. График экспериментальной зависимости a = f2(m) оказался прямой линией (в пределах погрешности измерений), проходящей через начало координат, следовательно, зависимость (4) подтверждена экспериментально, а следовательно, справедлив второй закон Ньютона, взятый за основу при выводе этого выражения. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
