кр. КР №2. Изучение рациональных чисел в курсе математики основной школы
 Скачать 1.84 Mb. Скачать 1.84 Mb.
|
|
Изучение рациональных чисел в курсе математики основной школы Сформулируйте определения рационального числа, десятичной дроби. Рациональное число – это число, которое можно представить в виде обыкновенной дроби 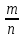 , числитель m – целое число, а знаменатель n – натуральное число. , числитель m – целое число, а знаменатель n – натуральное число.Десятичная дробь – это дробь со знаменателем 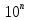 , где n — натуральное число. , где n — натуральное число.Какие из следующих чисел являются дробными числами, дробями, десятичными дробями: 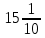 ; ; 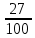 ; 9,04; 17,00; ; 9,04; 17,00; 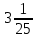 ? ?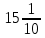 – дробное число, дробь, десятичная дробь; – дробное число, дробь, десятичная дробь; 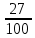 – дробное число, дробь, десятичная дробь; – дробное число, дробь, десятичная дробь;9,04 – дробное число, дробь, десятичная дробь; 17,00 – дробь, десятичная дробь; 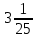 – дробное число, дробь. – дробное число, дробь.7,3500=7,35. Какое теоретическое положение лежит в основе приведенного упрощения десятичной дроби? Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби. ВНИМАНИЕ!!! Нельзя удалять нули, расположенные не в конце десятичной дроби!!!! Способ записи десятичных дробей является обобщением записи натуральных чисел. В записи натурального числа значение цифры зависит от того, в каком разряде она находится. Единицы двух соседних разрядов отличаются друг от друга в 10 раз. Для записи десятичных дробей используют новые разряды, которые пишут справа от разряда единицы, поставив после него запятую. При чтении десятичной дроби сначала называют её часть, стоящую до запятой с добавлением «целых», а затем часть, стоящую после запятой, с добавлением последнего разряда. Из приведенного примера 7,3500=7,35 видно, что в десятичной дроби после запятой стоит столько же цифр, сколько цифр в числителе дробной части соответствующей ей обыкновенной дроби. 3500/10000=35/100Если в первой дроби мы числитель и знаменатель разделим на 100, тогда увидим, что эти дроби равны. Может ли десятичная дробь быть неправильной? Нет. Понятие правильной и неправильной дроби относятся к обыкновенным дробям. Можно ли при округлении десятичной дроби до сотых получить натуральное число? Да. Например: 5, 997 ≈ 6. При округлении дробной части десятичной дроби пользуемся правилами округления. Подчёркиваем цифру округляемого разряда. Вертикальной чертой отделяем все цифры, стоящие справа от округляемого разряда. Если справа от подчёркнутой цифры стоит цифра 0, 1, 2, 3или4, то подчёркнутую цифру оставляем без изменений, а все цифры после вертикальной черты отбрасываем. Если справа от подчёркнутой цифры стоит цифра 5, 6, 7, 8или 9, то к подчёркнутой цифре добавляем 1, а все цифры после вертикальной черты отбрасываем. Округлим 41,998 до сотых. 41,998 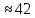 Мы видим, что при округлении десятичной дроби, как в нашем примере, до сотых можно получить натуральное число. Мы видим, что при округлении десятичной дроби, как в нашем примере, до сотых можно получить натуральное число.Представьте в виде обыкновенной дроби число -7,8(4). -7,8(4) = 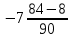 = = 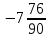 = = 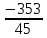 В смешанных периодических дробях между запятой, отделяющей целую часть от дробной, и периодом могут присутствовать другие цифры. Смешанные периодические дроби следуют немного другим законам перевода в обыкновенные. Количество знаков в знаменателе остаётся равным количеству знаков после запятой, включая в период, но теперь знаменатель будет состоять не только из 9, но и из 0, где количество 9 – это количество цифр в периоде, а количество 0 – это количество цифр между запятой и периодом. Числитель же рассчитывается через разность числа записанного после запятой, включая период, и числа, представляющего набор цифр между запятой и периодом. Если каждому действительному числу поставить в соответствие пятую цифру после запятой в его десятичной записи, то будет ли это соответствие функцией? Ответ поясните. Нет, т.к. нарушается единственность образа. Например: 8 = 8,000000 = 7,(9) Запишите в виде бесконечной десятичной дроби сумму 0,(31) и 2,(125). 0,313131+2,125125=2,(438256) Различны ли понятия дроби и дробного числа? Различны. Дробь — это число, составленное из целого числа долей единицы. Дробное число — это рациональное число вида 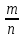 , где m – целое число, n – натуральное.Следует заметить, что в учебнике иногда происходит смешение понятий «дробь» и «дробное число». Так, в младших классах дробь трактуется как число, составленное из нескольких долей единицы. Одно и то же число можно записать разными дробями. Так, например, дроби 2/3, 6/9, 22/33, являются записями одного и того же числа. Дроби 8/8,24/3, служат для записи целых чисел, дроби 7/8, или 8/23, служат для записи дробных чисел. Таким образом, дробь может служить записью не только дробного, но и целого числа. , где m – целое число, n – натуральное.Следует заметить, что в учебнике иногда происходит смешение понятий «дробь» и «дробное число». Так, в младших классах дробь трактуется как число, составленное из нескольких долей единицы. Одно и то же число можно записать разными дробями. Так, например, дроби 2/3, 6/9, 22/33, являются записями одного и того же числа. Дроби 8/8,24/3, служат для записи целых чисел, дроби 7/8, или 8/23, служат для записи дробных чисел. Таким образом, дробь может служить записью не только дробного, но и целого числа.Какие виды десятичных дробей рассматриваются в школьном курсе математики? Бесконечные чистые периодические; 23,123456789123456789…=23,(1233456789). Бесконечные непериодические; 3,12986579498123… Смешанные периодические; 113,4578905905…905…=113,4578(905) Не смешанные; Правильные; 0,7 Не правильные; 7,2 С каким числовым множеством связано множество бесконечных периодических дробей? Множество действительных чисел - рациональных. С каким числовым множеством связано множество бесконечных непериодических дробей? Множество действительных чисел - иррациональных. Выполняя совместные действия с обыкновенными и десятичными дробями, учащиеся часто осуществляют перевод обыкновенной дроби в десятичную. Сформулируйте признак возможности перевода обыкновенной дроби в конечную десятичную. Приведите примеры, иллюстрирующие применение этого признака. Если знаменатель обыкновенной дроби не содержит никаких простых множителей, кроме 2 и 5, то эту дробь можно перевести в десятичную. Если знаменатель обыкновенной дроби содержит хотя бы один простой множитель отличный от 2 и 5, то эту дробь нельзя перевести в десятичную. 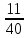 = = 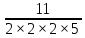 = 0,275 = 0,275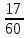 = = 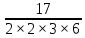 нельзя преобразовать в конечную десятичную дробь, потому что в её знаменателе кроме множителей 2 и 5, есть 3. нельзя преобразовать в конечную десятичную дробь, потому что в её знаменателе кроме множителей 2 и 5, есть 3.Как бы вы объяснили учащимся, что такое десятичная дробь? Какие знания необходимо актуализировать с учащимися для введения понятия десятичной дроби? Неизвестная нам до этого времени форма записи чисел, например: 98,7; 103,5; 5,29, получила название «десятичная дробь». Известно, что единица каждого разряда в натуральном числе, кроме разряда единиц, состоит из десяти единиц разряда, которые находятся справа. Другими словами, единица каждого такого разряда в десять раз больше, чем единица разряда, которая стоит справа, и в десять раз меньше, чем единица, стоящая слева, т.е. составляет его 10-тую часть. С помощью десятичных дробей можно записывать дробные числа. В этом случае слева от запятой стоят цифры целой части числа, справа – дробной части. Цифры дробной части называются десятичными знаками. Число 1,695 состоит из трёх десятичных знаков: 6, 9 и 5.Чтоб прочитать десятичную дробь, надо:- прочитать целую часть дроби как натуральное число и сказать слово «целых»;- прочитать, дробную часть как натуральное число не обращая внимания на нули в начале дробной части, сказать название последнего разряда дробной части. Чтобы десятичную дробь записать в виде обыкновенной дроби, нужно:1) то, что стоит до запятой, записать целой частью числа;2) то, что стоит после запятой, записать в числитель дробной части, а в знаменатель после единицы записать столько нулей, сколько цифр после запятой. Десятичную дробь и читают так же, как обыкновенную. Например, 7,63 – семь целых шестьдесят три сотых; 0,107 – нуль целых сто семь тысячных; 3,005 – три целых пять тысячных. Место темы «Десятичные дроби» в логике построения содержания различных курсов математики 5-6-х классов. Цели обучения теме. Учебник: Математика 5 класс: учебник для общеобразовательных учреждений. / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд –3 — 31-е изд., испр. и доп – М.: Мнемозина, 2013. До изучения темы «Десятичные дроби» изучается тема «Обыкновенные дроби». После изучения темы «Десятичные дроби» изучается тема «Умножение и деление десятичных дробей». Цели обучения теме. выделить методические особенности в обучении теме «Десятичные дроби»; разработать методику изучения фрагментов содержания: Ввести понятие десятичной дроби. Вести работу по формированию навыков чтения и записи десятичных дробей (изучение и первичное закрепление алгоритма чтения и записи десятичных дробей). Разработайте методику введения правила сложения обыкновенных дробей. Сформулируйте вопросы, на которые необходимо ответить при разработке этой методики. Сложение дробей с одинаковыми знаменателями. Для этого нужно начертить на доске квадрат и разделить его на 9 равных частей (долей), для того чтобы учащиеся убедились, что каждая часть (доля) может выражаться дробью. Предложить учащимся закрасить две такие части одним цветом, три части - другим цветом и поставить перед ними вопрос: «Сколько всего закрашенных частей». Ученики ответят, что закрашено 5 частей. Если записать сказанное в виде дроби, то получится 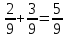 После этого учащиеся сами смогут сформулировать правило сложения дробей с одинаковыми знаменателями. (Чтобы сложить обыкновенные дроби с одинаковыми знаменателями, надо составить дробь, у которой числитель равен сумме числителей данных дробей, а знаменатель остается без изменения. Это правило записывается так: 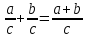 ). ). Замечание: Если в результате сложения дробей получится сократимая дробь, то её можно сократить.Пример 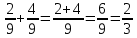 Далее можно переходить к правилу сложения дробей с разными знаменателями. Чтобы сложить обыкновенные дроби с разными знаменателями, нужно сначала привести их к наименьшему общему знаменателю, затем, используя правило сложения дробей с одинаковыми знаменателями, продолжать выполнять сложение.Например, чтобы найти сумму дробей 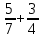 , нужно найти наименьшее общее кратное знаменателей данных дробей. НОК (7,4) = 28. Следовательно, наибольшим общим знаменателем дробей , нужно найти наименьшее общее кратное знаменателей данных дробей. НОК (7,4) = 28. Следовательно, наибольшим общим знаменателем дробей 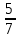 и и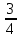 является число 28. Дополнительные множители 28:7=4 и 28:4=7. является число 28. Дополнительные множители 28:7=4 и 28:4=7.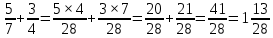 Вопросы, на которые необходимо ответить при разработке этой методики Что хотим донести до ребят при объяснение данной темы? Какими примерами будем пользоваться при объяснение данной темы? Какой аппаратурой будем пользоваться? Какие цели и задачи поставили перед тем как начать объяснения? Проанализируйте достоинства и недостатки методики изучения действий с десятичными дробями до изучения действий с обыкновенными дробями. При введении десятичных дробей раньше обыкновенных, удобством будет то, что: Десятичные дроби могут быть введены при рассмотрении десятичной системы нумерации целых положительных чисел (первая разделяющая единица после запятой – десятые доли единицы, а следующая – сотые и т.д.); Все арифметические действия выполняются для десятичных дробей проще; Десятичные дроби имеют большое практическое применение, чем обыкновенные. Минусом будет то, что из частного случая нельзя делать общие выводы и придётся всю теорию для обыкновенных дробей объяснять заново. Составьте набор упражнений, способствующих усвоения различий между понятиями «дробь» и «дробное число»? Какие из следующих чисел являются дробными числами, дробями? 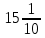 ; ; 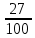 ; 9,04; 17,00; ; 9,04; 17,00; 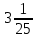 Выберите дроби равные двум 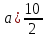 ; ; 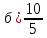 ; ; 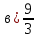 ; ; 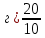 ; ; 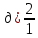 Что должны уметь делать ученики после изучения понятия десятичной дроби? Приведите примеры упражнений для проверки перечисленных вами умений. Ученики должны:Определять понятие десятичной дроби. Читать и записывать десятичную дробь. Записывать обыкновенную дробь со знаменателем 10, 100 ,1000, и т.д. в виде десятичной дроби. Знать принцип записи цифр после запятой. Примеры упражнений: Прочитать дроби 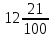 ; ; 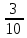 ; ; 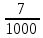 . .Записать в виде десятичной дроби 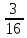 ; ; 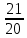 ; ; 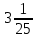 Записать в виде десятичной дроби 4 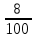 ; ; 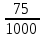 ; ; 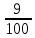 ; ;Какие ошибки могут допускать учащиеся при сложении десятичных дробей (два-три примера). Покажите методику работы по их преодолению. Неправильная запись: 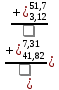 Правильная запись: 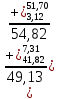 Если исходные десятичные дроби имеют разное количество знаков (цифр) после запятой, то к дроби с меньшим количеством десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять в дробях количество знаков после запятой. Методика работы: уравниваем количество знаков после запятой; записываем десятичные дроби друг под другом так, чтобы запятые были друг под другом; выполняем сложение десятичных дробей, не обращая внимания на запятые, по правилам сложения в столбик натуральных чисел; ставим в ответ запятую под запятыми. Разработайте фрагмент урока: «Введение понятия десятичной дроби». Разработка должна содержать: цель урока, планируемые результаты, описание оборудования, разработку этапов: 1) мотивационно-целевой; 2) процессуально-познавательный; 3) рефлексивно-оценочный. Класс: 5Тип урока: изучение нового материала. Цель урока: Ознакомить учащихся с понятием десятичной дроби, формировать умение читать и записывать десятичные дроби. Оборудование: Учебник: (Математика 5 класс: учебник для общеобразовательных учреждений. / И.И.Зубарева, А.Г.Мордкович. –14-е изд., испр. и доп – М.: Мнемозина, 2013.) Проектор, компьютер. Планируемые результаты: Метапредметные результаты: умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи в учёбе и познавательной деятельности, развивать мотивы и интересы своей познавательной деятельности; умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками; работать индивидуально и в группе; формулировать, аргументировать и отстаивать своё мнение. Личностные результаты: способность к планированию собственной индивидуальной и групповой деятельности; повышение своего образовательного уровня и уровня готовности к продолжению обучения с использованием десятичных дробей; владение способами записи обыкновенной дроби в виде десятичной; формирование ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию; формирование осознанного, уважительного и доброжелательного отношения к другому человеку, его мнению, мировоззрению. Регулятивные результаты: видеть, понимать, решать учебную задачу урока (под руководством учителя), учиться самоконтролю и самоанализу Познавательные результаты: дать целостное представление об изучаемом понятии, научить правильно читать и записывать обыкновенные дроби, применять полученные знания при решении задач, применять полученные знания вне урока. Коммуникативные результаты: умение слышать, слушать и понимать товарища, планировать и согласованно выполнять совместную деятельность, распределять роли, взаимно контролировать действия друг друга, уметь договариваться, вести дискуссию, правильно выражать свои мысли, оказывать поддержку друг другу, эффективно сотрудничать как с учителем, так и со сверстниками. Этапы: Мотивационно-целевой Выполняются задания со слайда, обсуждение результатов происходит фронтально. Данный вид работы позволяет повторить понятие смешанного числа, алгоритм выделения целой части в неправильной дроби. В каждом столбике последние два задания представляет собой примеры по новой теме и потому их решение наталкивает на проблему, решение которой предлагается рассмотреть на уроке. Таким образом, учащиеся приходят к выводу о недостатке знаний по теме «Десятичная запись дробных чисел», в частности, их записи и чтения. Предлагают рассмотреть «Десятичную запись дробных чисел» в качестве темы и самостоятельно формулируют цель урока. Процессуально-познавательный Работая с именованными числами, ребята опять встречаются с «особыми» дробями и необходимостью записывать их иначе, чем обыкновенные дроби. При работе с новым материалом используется информационный модуль и слайды. Далее ученики делают вывод о том, что любое число, знаменатель дробной части которого выражается единицей с одним или несколькими нулями, можно записать в виде десятичной дроби. Используя этот же ЭОР (электронные образовательные ресурсы), читаем десятичные дроби. Рефлексивно-оценочный В ходе подведения итогов изученного на уроке обсуждаем, что нового узнали на уроке, достигли ли поставленной в начале урока задачи. Учащиеся повторяют изученный материал, анализируют причины своих ошибок, проговаривая их. Выясняют, вопрос о достижении (или не достижении) задач, поставленных в начале урока. Изучение действительных чисел Может ли сумма двух иррациональных чисел быть рациональным числом? Если да, приведите примеры. Может. Например: Число А = 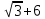 . Число В = - . Число В = -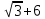 . Сумма чисел А и В = 12 . . Сумма чисел А и В = 12 .Может ли произведение двух иррациональных чисел быть рациональным числом? Если да, приведите примеры. Может. Например: Число А = 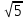 . Число В = . Число В = 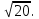 Произведение чисел А и В = 10 Произведение чисел А и В = 10Каких чисел больше – рациональных или иррациональных? Если рациональных чисел бесконечное множество, и иррациональных чисел подобное же множество. Но на каждое ОДНО рациональное число приходится множество дополнительных иррациональных чисел (путём математического сложения, умножения или деления этого рационального с множеством иррациональных). Таким образом, иррациональных чисел больше! Приведите пример иррационального числа, заключенного между числами 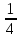 и 0,3. и 0,3.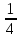 < x < 0,3 < x < 0,30,25< x < 0,3 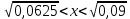 Пример x : 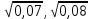 Постройте с помощью чертежных инструментов 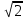 , , 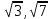 . .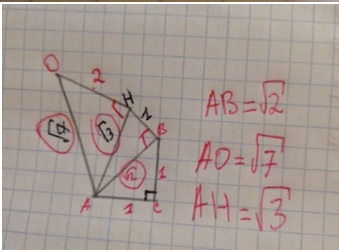 Какое действие, выполнимое на множестве действительных чисел, не выполняется на множестве комплексных чисел? Сравнение чисел. Докажите, что 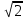 не является рациональным числом. не является рациональным числом.Пусть √2 рациональное, т.е. √2 = a/b, где a и b - целые числа, не имеющие общих делителей. Тогда 2 = a²/b², т.е. a² = 2b². Следствие - a² - четное. Но если a² - четное, то и а - четное, т.е. а = 2x. Тогда 4x² = 2b² => b² = 2x², т.е. b - тоже четное. А это противоречит исходной посылке (a и b не имеют общих делителей). Следовательно √2 нельзя представить в виде a/b, значит это число не является рациональным. Выделите подходы к введению понятия «иррациональное число» в учебниках разных авторских коллективов. В некоторых учебниках (Д. К. Фаддеев и др.) используется подход Кантора. Второй подход к введению понятия реализован в учебнике алгебры по ред. С. А. Теляковского(геометрический подход). Третий подход реализован в учебниках алгебры Ш. А. Алимова и др.(Сформулировано определение. Приведены примеры). Приведите примеры использования геометрического материала при введении квадратных корней из неотрицательных чисел. Постройте с помощью чертежных инструментов 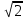 , , 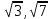 . .Предложите вариант методики введения понятия «Арифметический квадратный корень из неотрицательного числа». Методика введения квадратного корня из неотрицательного числа (Н.Я. Виленкин). 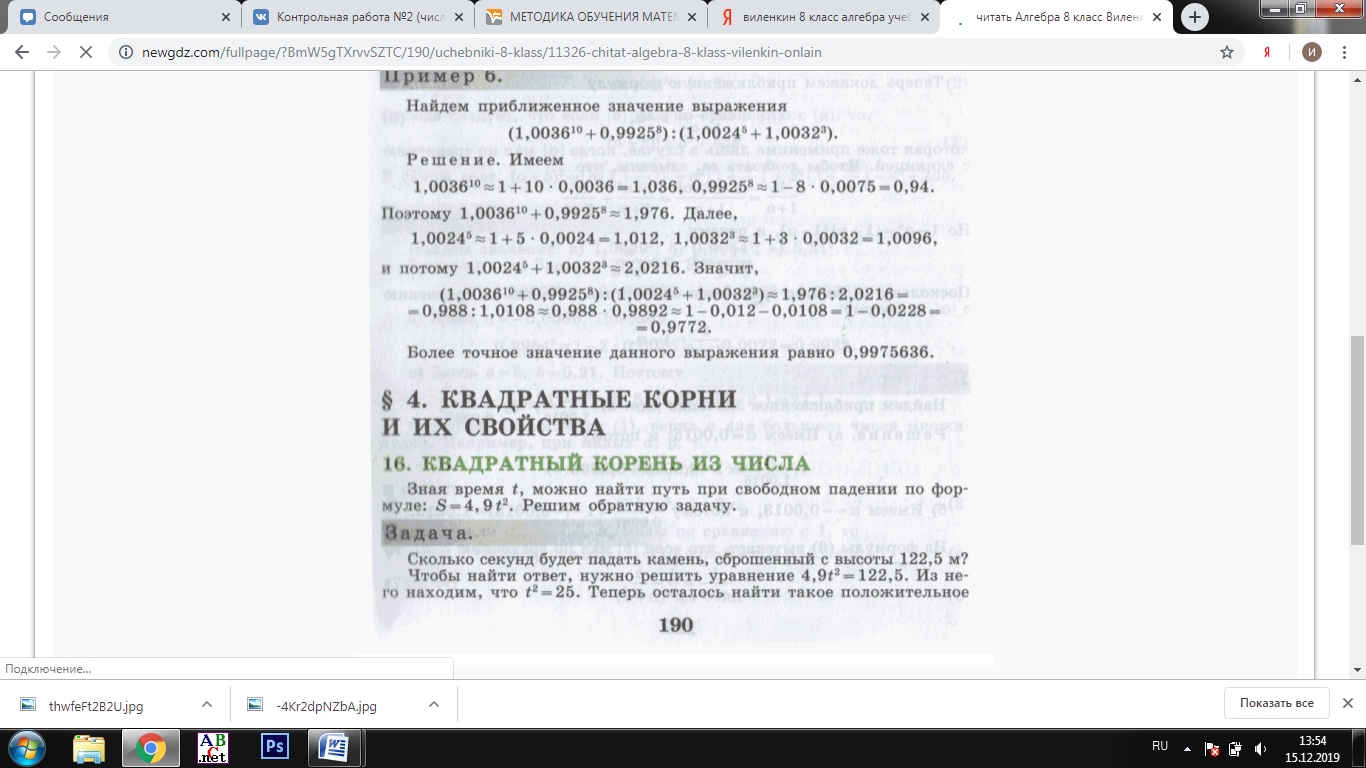 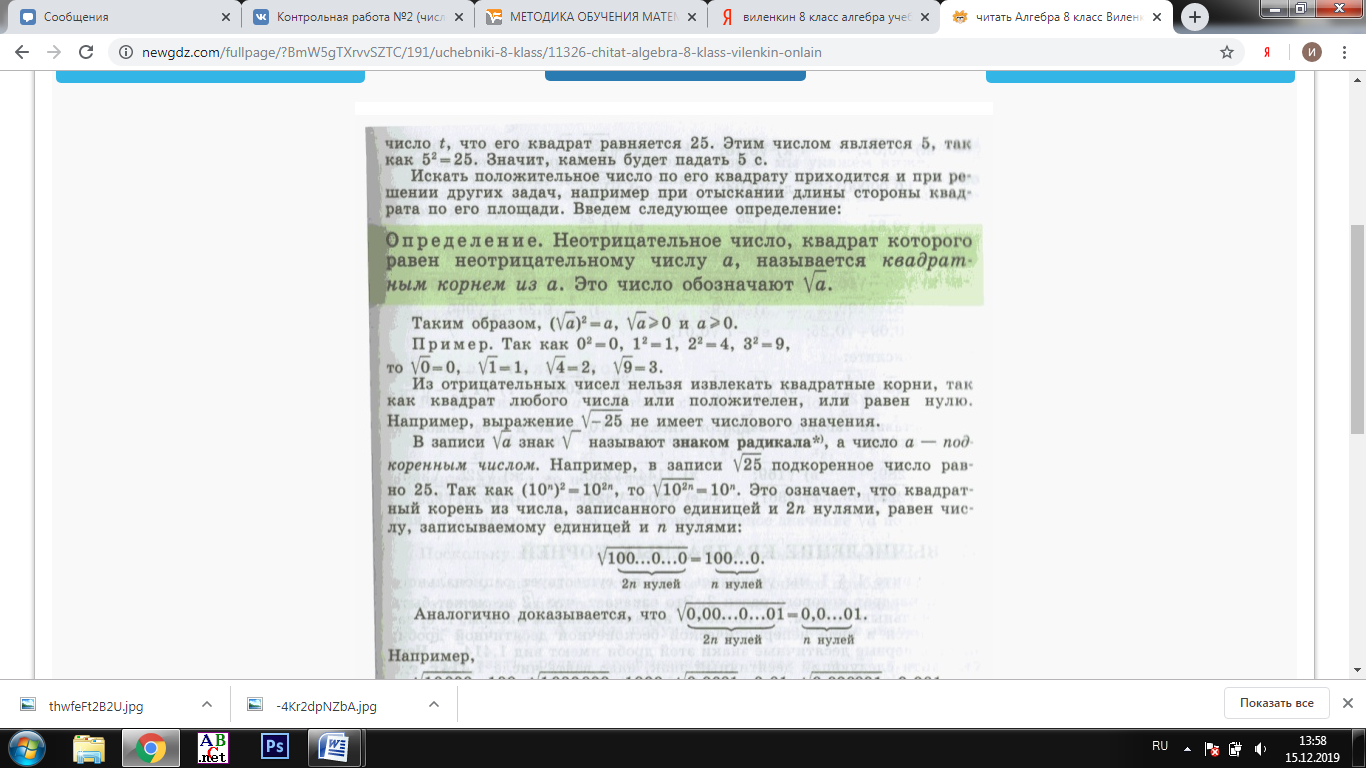 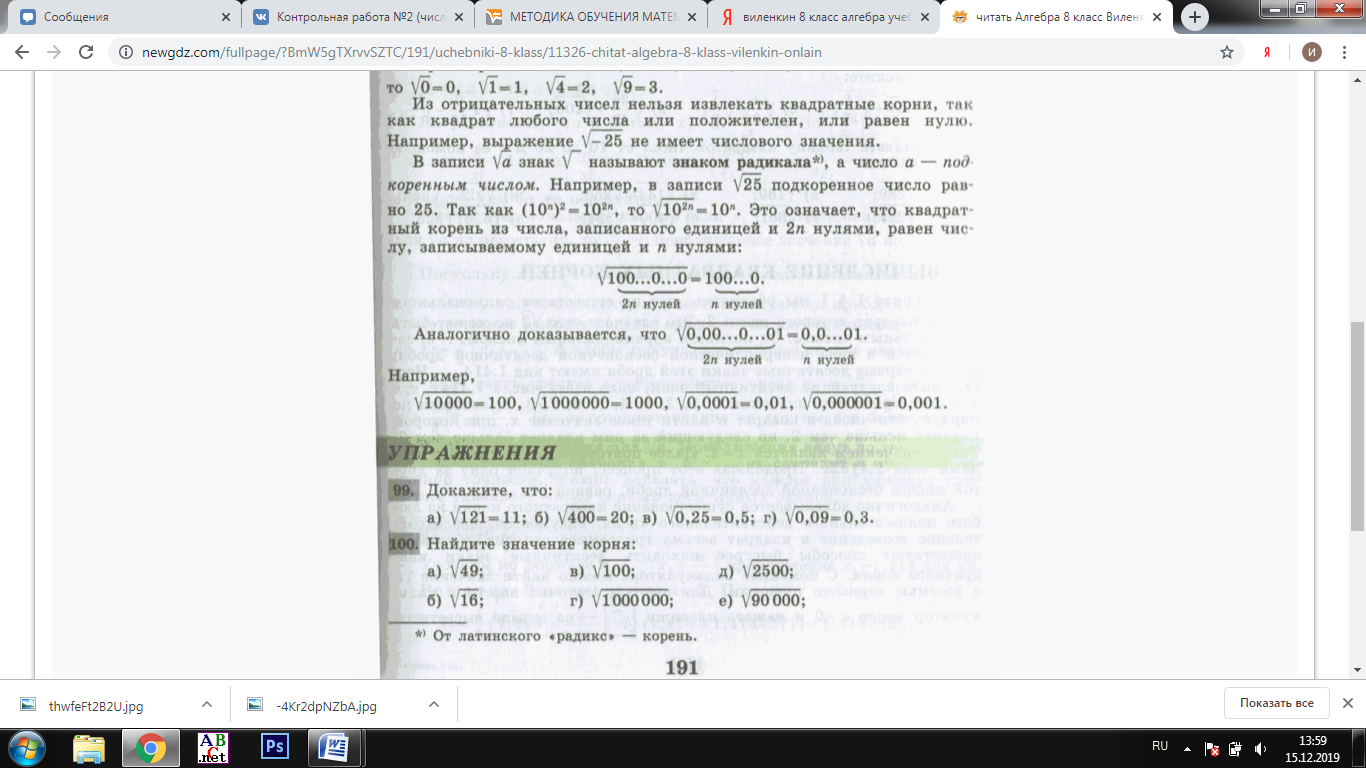 Предложите вариант дифференцированной контрольной работы по теме «Арифметический квадратный корень из неотрицательного числа». Работа на 3 Сравните числа: а) Внесите множитель под знак корня: а) Вычислите: а) Работа на 4 Внесите множитель под знак корня: а) Упростите выражение: а) Вынесите множитель из-под знака корня Работа на 5: Упростите выражение: Расположить числа в порядке возрастания: а) Упростите выражение: Что больше 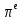 или или 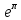 ? ?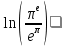 = = 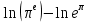 = =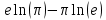 = = 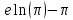  = = 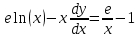 x = x = 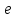 при x> при x>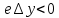 следовательно следовательно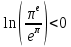 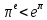 |
