емтихан. жауаптары емтихан алгебра. Жиын. Жиындара мысалдар. Жиындарды берілу тсілдері. Жиын трлері. Санды жиындар. Жиын
 Скачать 95.1 Kb. Скачать 95.1 Kb.
|
Жиын. Жиындарға мысалдар. Жиындардың берілу тәсілдері. Жиын түрлері. Сандық жиындар. Жиын деп белгілі бір объектінің белгілі қасиеттеріне байланысты топтастырылуы.Жиын деп белгілі математикалық объектілердің жиынтығын түсінеміз. Ол объектілер жиынның элементтері деп аталып, кіші әріптермен, ал жиынның өзі бас әріппен белгіленеді. а элементі А жиынына тиістілігін а Жиі қолданылатын кванторлар: х - кез келген, ׃ ( | ) – мынадай, қасиетін сипаттау үшін; Жиынға енетін элементтер саны шенеулі немесе шексіз көп болуы мүмкін. 1-мысал: а) қазақ алфавитінің әріптер жиыны (42 элемент бар); ә) натурал сандар жиыны ( Жиын түрлері. Ақырлы жиындеп осы жиынның элементтерінің санына тең болатын натурал сан табылатын жиынды айтады. Ақырлы емес жиын ақырсыз жиын деп аталады. Ақырлы А және В жиындары тек қана бірдей элементтерден құралса, тең жиындар деп аталып, А=В деп белгіленеді. Егер ақырлы А жиынында ақырлы В жиынына тиісті емес элемент бар болса, және керісінше, онда олар тең емес жиындар деп аталады. 2-мысал. {0, 1, 2}={1, 2, 0}, {0, 1} Жиындардың берілу тәсілдері. Мүшелерін (элементтерін) тізіп жазу арқылы. Ақырлы жиын 2. Сипаттау арқылы. Мысалы жиынның кез келген х мүшесі р(х) қасиетіне ие болсын, онда осы элементтерден тұратын С жиыны былай беріледі: С={х Осы сияқты анықталған жиындар Q={ А және В жиындары берілсін. Егер А жиынының кез келген х элементі В жиынында да жатса, онда А жиыны В жиынының ішкі жиыны деп аталады. А Егер В жиынының А ішкі жиыны В жиынынан және Ø-ден өзгеше болса, онда ол меншікті ішкі жиыныдеп аталады. Кванторлар тілінде, А Ø кез келген жиынның ішкі жиыны болады: Ø Қасиеттері: а) А ә) А б) А В жиынының В және Ø ішкі жиындары оның меншіксіз ішкі жиындарыдеп аталады. Егер жиын ең болмағанда екі элементтен тұрса, онда оның меншікті ішкі жиындары болады. Мысалы: А = {а, в} жиынының ішкі жиындары: {а}, {в}, {Ø}, {а, в}. Бұл ішкі жиындардың ішінде {а}, {в}- меншікті, ал {а, в}, {Ø}- меншіксіз болып табылады. 2. Жиындар үстінде амалдар.Жиындардың бірігуі, қиылысуы, айырмасы және жиындардың декарттық көбейтіндісі. Эйлер-Винн диаграммасы. U (универсум) деп кең жиынды белгілейік, яғни элементтер осы жиыннан алынып отыратын болсын. Эйлер 1. Ең болмағанда А жиынына немесе В жиынына тиісті элементтер жиынын А және В жиындарының бірігуі(қосындысы) (А 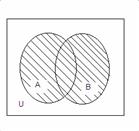 А А А «Бірігу» амалын жалпыласақ, 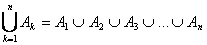 2. А жиынына да, В жиынына да тиісті элементтер жиынын А және В жиындарының қиылысуы(көбейтіндісі) (А А
А «Қиылысу» амалын жалпыласақ, 3. А жиынына тиісті, бірақ В жиынына тиісті емес элементтер жиынын А және В жиынының айырымы (А\В) деп айтады. А\В = {х:х
А \ В={2,4}, В \ С={1,3}, А\С=А. 4. А және В жиындарының симметриялық айырмасы (А А
5. U\A жиыны А жиынының толықтауышы деп аталып, 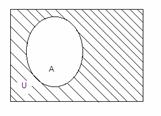 Унивесум U={1,2,3,4,5,6,7,8,9} болса, онда Жиындардың декарттық (тура) көбейтіндісі Математикада жиындардың жай элементтері ғана емес, сонымен бірге олардың реттелген жұп элементтері де кездеседі. (а1,а2,...,аn) элементтері реттелген жиын берілсін, оны жиынтық, вектор, кортеж деп те атайды, аі –жиынның і-ші мүшесі. (а1,а2,...,аn) – жиынтығының ұзындығы деп n компоненталар санын айтамыз. А және В жиындарының тура немесе декарттық көбейтіндісі деп (а,в) жұбының жиынын айтамыз. Мысалдарқарастырып өтейік. 1. A={1,2}, B={1,2,3} жиындары берілсін. Бұл жиындар үшін тура көбейтінділер 2. R – нақты сандар жиыны берілсін. Онда 3.Группа. Сақина. Өріс. Алгебралық амалдар. Алгебралық амалдардың қасиеттері. Бейтарап элементтер. Анықтама. Группа деп а×в бинарлы операциясы үшін, келесі шарттар орындалатын G жиындарды айтамыз. Ассоциативтілік: (ав)с=а(вс) кез келген екі g1€G және g2€G элементтері үшін әрбір Кез-келген G-ның а элементі жиын үшін мына элементтері орындалса: а€G, а-1€G, аа-1= а-1a=e Группа анықтамасындағы кері амалдың болуы шартын келесі шарттармен ауыстыруға болады: 10. Кез келген 20. Әрбір g€G элементі үшін gOf=e, fOg=e теңдіктерін қанағаттандыратын f кері элементі бар болады. Анықтама. Егер P жиынының кез келген a,b,c элементтері үшін жоғарыдағы 10 – 50 қасиеттері орындалатын болса, онда қосу және көбейту амалдары анықталған P жиыны сақина деп аталады және егер P жиынында 0 -ден өзгеше элементтер болып, жоғарыдағы 10 – 70 қасиеттері орындалатын болса, онда P жиыны өріс деп аталады. С1) С2) С3) С4) С5) С6) С7) Нақты сандарды қосуға, көбейтуге және кері амалдарды алу және бөлуге болады. Нақты сандар келесі үш қасиеттке ие: Қосу бойынша коммутативті группа құрайды, бірлік элемент ретінде 0-ді алады және солай аталады. Егер 0-ді алып тастаса, көбейту бойынша коммутативті группа құрайды. Кез келген а, в, с үшін диструбутивті заңға бағынады: а(в+с)=ав+вс Анықтама: Егер қандай да бір жиында жоғарыда мысалда көрсетілген екі бинарлы амал қолданса, онда мұндай жиын өріс д.а Анықтама. Егер кез келген a€A элементі үшін e€A элементі табылып Анықтама. A жиынындағы алгебралық амал деп A2 -нің әрбір Мысалы, қосу, көбейту және азайту амалдарын R нақты сандар жиынындағы амалдар ретінде қарастыруға болады. Сонымен қатар, үш өлшемді кеңістіктің векторлар жиынындағы векторлық көбейтінді амалы, Z+ бүтін оң сандар жиынындағы дәрежеге шығару амалы, алгебралық амалдар болып табылады. Алгебралық амалдарды белгілеу үшін 15.16. Пікірлер және пікірлер үстінде амалдар. Пікірлер алгебрасының формулалары. Пікір деп тек не «ақиқат», тек не «жалған» болатын сөйлемді айтады. Математикалық логикада пікірдің не тек ақиқат, тек не жалған болу қасиеті ғана маңызды роль атқарады, ал оның формасы мен құрылымы дерлік ешқандай роль атқармайды. Мысал. Келесі пікірлерді карастырайық: «Париж-Италияның астансы»,«3<5», «әрбір үшбұрышта биссектриса қарама –қарсы қабырғаны қақ бөледі». Пікірлер үлкен латын әріптерімен белгіленеді: А,В,..., ал олардың мәндерін «ақиқат» немесе «жалған» деп белгілейміз. Кез келген А және В екі пікір берілген болсын: 1.Бұл екі пкір үшін бірінші амал нәтижесіндегі алынған пікірді А&В деп белгілейміз және бұл пікір А ның да В ның да «ақиқат» пікір болғанда ғана «ақиқат » болады. Бұл амал логикалық көбейту деп аталады. Кәдімгі сөйлеуде бұл амалға «және» деген шылау сәйкес келеді. 2. А және В пікірлерге қолданылатын екінші амал А˅В деп өрнектеледі және былай анықталады: ол алғашқы пікірлерді ең болмаса біреуі «ақиқат» болса, ақиқат болады.Бұл амал логикалық қосу деп аталады. Кәдімгі сөйлеуде бұл амалға «немесе» шылауы сәйкес келеді. Бірақ «немесе» шылау «не, не» деген мағынаны бермейді. 3. Келесі амал А→В мен белгіленіп, бұл пікір тек А ақиқат , ал В жалған болғанда ғана жалған болады. А- себеп, В- салдар деп аталады. Бұл амал логикалық еру деп аталады. Кәдімгі сөйлеуде бұл амал «егер, онда » байланысқа сәйкес келеді. Бұл А→В пікір А жалған болғанда, В ақиқат болғанса да жалған болғанса да ақиқат болады. Бұдан жалғаннан ақиқатта жалғанда келіп шығатынын көреміз. Кәдімгі сөйлеуде , егер А жалған болса, «егер А болса, онда В» деген сөйлемнің мағынасы болмайды. Бірақ математикалық логикада мұндай түсінік қабылданбайды. 4. Келесі амал терістеу амалы деп аталады және 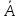 деп белгіленеді. Бұл А ақиқат болса, онда деп белгіленеді. Бұл А ақиқат болса, онда 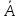 жалған, ал А жалған болса, онда жалған, ал А жалған болса, онда 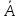 болатынын білдіреді. болатынын білдіреді. 5. Келесі амал эквиваленттік амал деп аталады және А  В деп белгіленед. Ол тек А және В ның екеуі бірдей ақиқат, не екеуі бірдей жалған болғанда ғана ақиқат болады. В деп белгіленед. Ол тек А және В ның екеуі бірдей ақиқат, не екеуі бірдей жалған болғанда ғана ақиқат болады. X,Y,Z,U,V,W, … кез келген пікірлер болсын олар тек не ақиқат («А») және жалған («Ж») мән қабылдайтын болсын. Бұлардан &, ˅, →, ͞ және амалдар арқылы күрделі пікірлер құрастыруымызға болады. Жоғарыда келтірілген амалдар басқашада аталады: &-амалы коньюкция амалы, ˅- дизьюнкция, → - импликация, ͞ - инверсия және - логикалық бірмәнділік деп те аталады. Бұл амалдар басқашада белгіленеді: & - ˄ және ∩ мен , ˅- 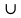 мен, → - ⸧ мен, ͞ - ⅂ мен, ал - ↔ және ≡ мен белгіленеді. мен, → - ⸧ мен, ͞ - ⅂ мен, ал - ↔ және ≡ мен белгіленеді.Пікірлер үстінде келтірілген амалдар арқылы басқа да барынша күрделі пікірлерді құруға болады. Мысалы, (А&В)˅С; ((А→В) 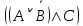 ). ).Әрбір формула оған кіретін А,В, ... әріптердің функциясы болады. Біз U және B формулаларды егер Х1,Х2,...,Хn - U және B ға кіретін барлық айнымалылардың жиынтығы болып, Х1,Х2,...,Хn дердің кез келген мәндерінде бұл формулалар бірдей мән қабылдаса, мәндес фомулалар деп атаймыз. Мәндес формулалаға тағыда бірнееше мысал келтірейік. 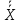 формула Х формулаға мәндес; формула Х формулаға мәндес; Х&У формула У&Х формулаға мәндес; Х&У формула У&Х формулаға мәндес;(Х&У)&Z формула Х&(Y&Z) формулаға мәндес; X˅Y формула Y˅Х формулаға мәндес; (X˅Y)˅Z формула Х˅(Y˅Z) формулаға мәндес; X&(Y˅Z) формула (Х&Y)˅(X&Z) формулаға мәндес; X˅(Y&Z) формула (Х˅Y)&(X˅Z) формулаға мәндес; 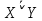 формула формула 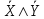 формулаға мәндес; формулаға мәндес;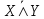 формула формула 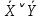 формулаға мәндес; формулаға мәндес;X˅X формула Х формулаға мәндес; X&X формула Х формулаға мәндес; X&„А” формула Х формулаға мәндес; X˅„А” формула „А” формулаға мәндес; Формулалар: 1. ⅂⅂X≡ Х ; екі рет терістеу заңы,  2. Х˄У ≡У˄Х ; коньюнкцияның коммутативтік заңы. 2. Х˄У ≡У˄Х ; коньюнкцияның коммутативтік заңы.3. X˅Y ≡Y˅Х; дизьюнкцияның коммутативтік заңы. 4. (Х˄У) ˄Z ≡ Х˄ (Y˄Z); коньюнкцияның ассоциативтік заңы. 5. (X˅Y)˅Z ≡Х˅(Y˅Z); дизьюнкцияның ассоциативтік заңы. 6. X˄(Y˅Z) ≡ (Х˄Y)˅(X˄Z); бірінші дистрибутивтік заңы. 7. X˅(Y˄Z) ≡ (Х˅Y)˄(X˅Z); екінші дистрибутивтік заңы. 8. ⅂ (X˅Y) ≡⅂X˄⅂Y; де Морган заңы. 9. ⅂ (X˄Y) ≡⅂X˅⅂Y; де Морган заңы. 10. X˅ Х ≡X; коньюнцияның идемпоненттік заңы. 12. X˄X ≡ Х; дизьюнцияның идемпоненттік заңы. 13. X˅⅂X≡„А” ; үшіншіні алып тастау заңы. 14. X˄⅂X≡„Ж”; қарама-қайшылық заңы. 15. X˅„А”≡ „А”; „А” мен „Ж” мәндердің қатысуымен амалдар заңы. 16. X˄„Ж”≡ „Ж”; „А” мен „Ж” мәндердің қатысуымен амалдар заңы. 17. X˅„Ж” ≡X; „А” мен „Ж” мәндердің қатысуымен амалдар заңы. 18. X˅„А”≡„А” ; „А” мен „Ж” мәндердің қатысуымен амалдар заңы. 19. X˄„А”≡X; „А” мен „Ж” мәндердің қатысуымен амалдар заңы. 20. X˅(X˄Y)≡X; жұту заңы. 21. X˄(X˅Y)≡X; жұту заңы. 22. X→Y≡⅂Y→⅂X; контропозиция заңы. |