|
|
Решение неравенств. К арточка 1. Справка Линейные неравенства
К арточка №1. Справка арточка №1. Справка
Линейные неравенства
ах 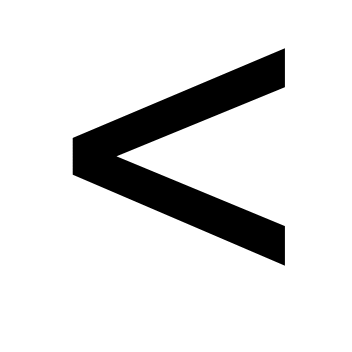 b (ах b (ах 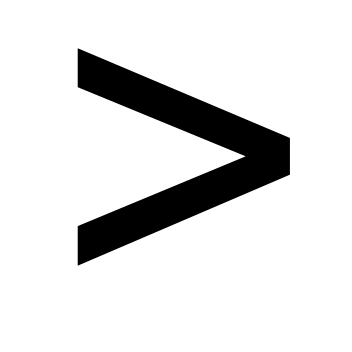 b, ах b, ах 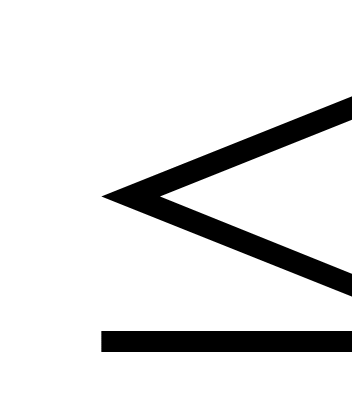 b, ах b, ах 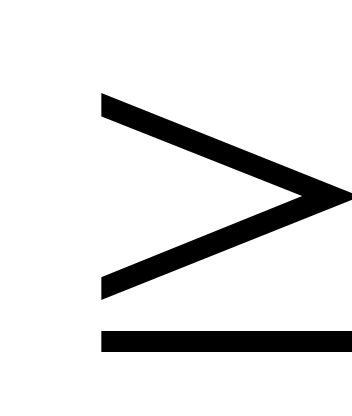 b) b)
х – переменная,
а, b – числа.
Неизвестное х в первой степени.
Как решать ах 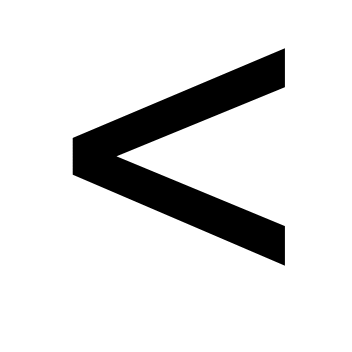 b b
1) а >0, х< 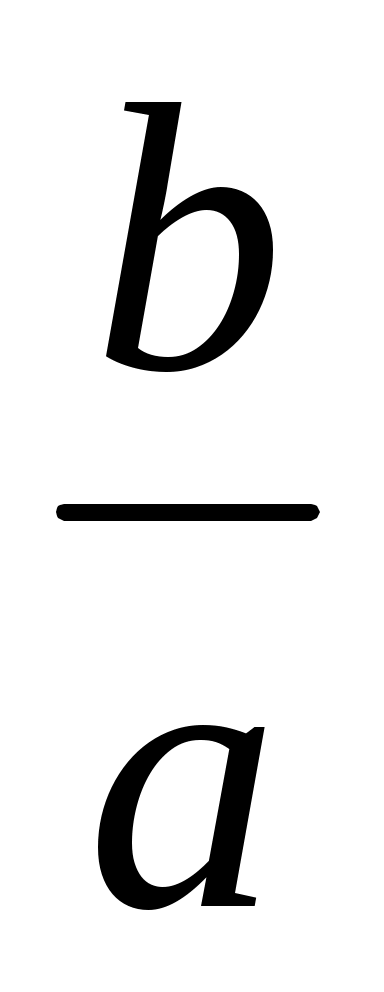 ;ах < b ;ах < b
2) а <0, х>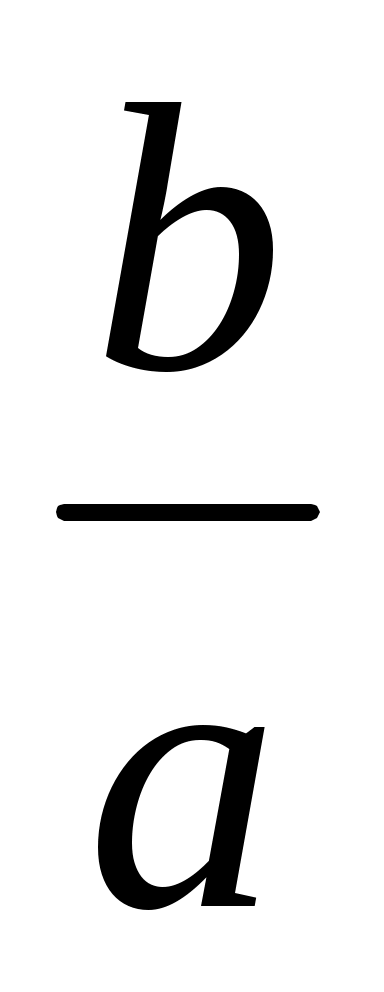 ; Меняем знак при отрицательном а ; Меняем знак при отрицательном а
  
|
К
Решить неравенство:
25х<125
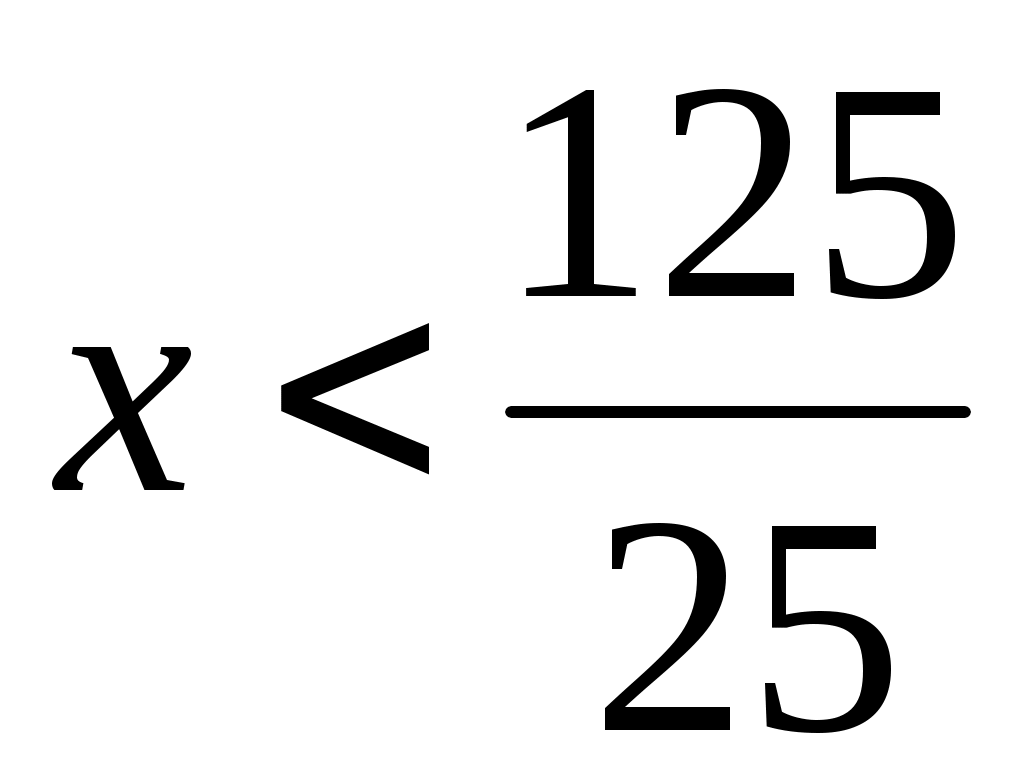
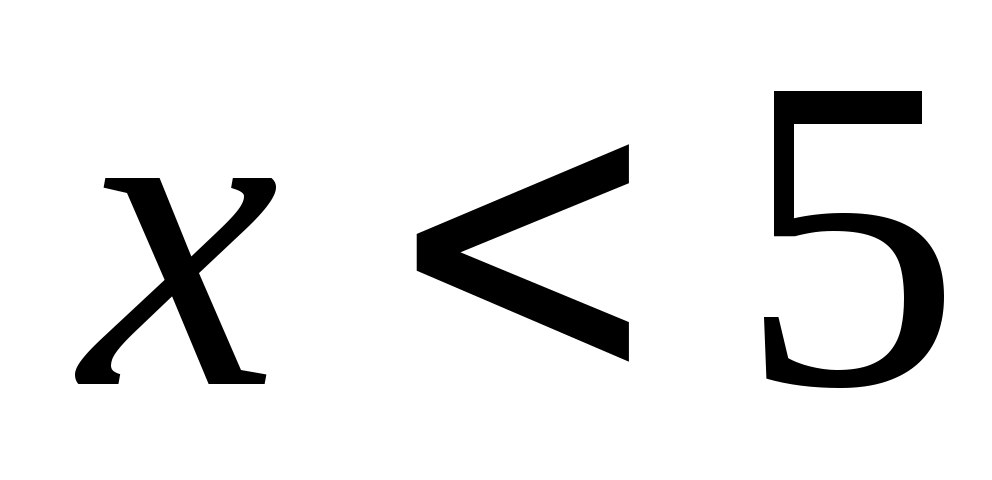 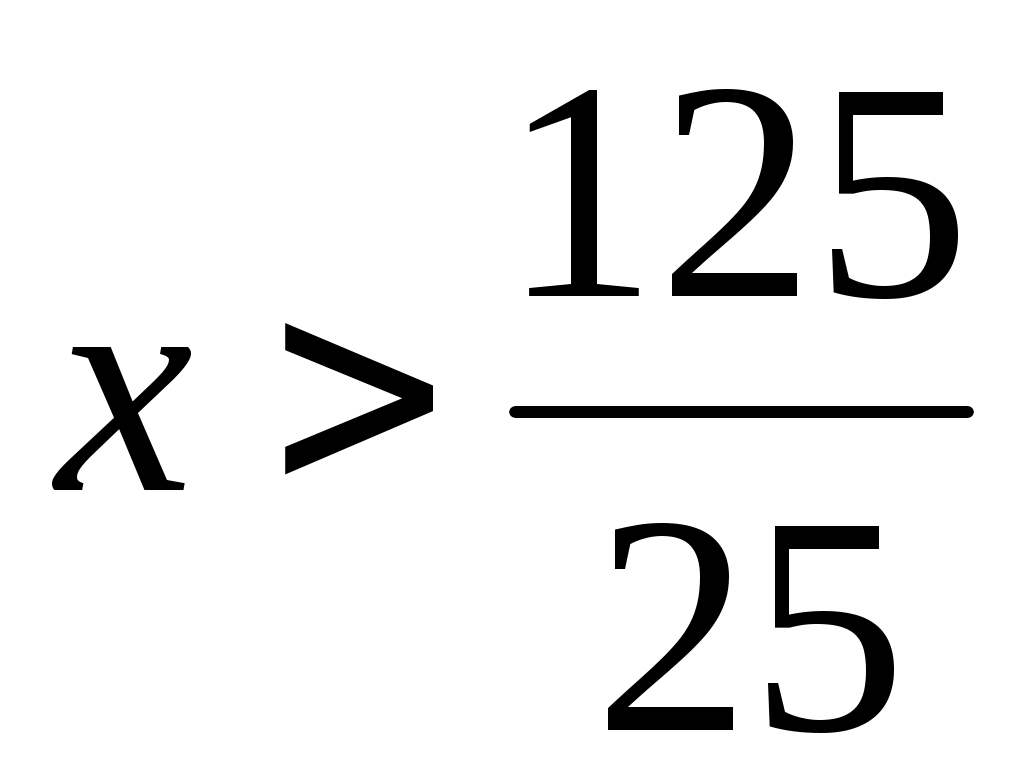 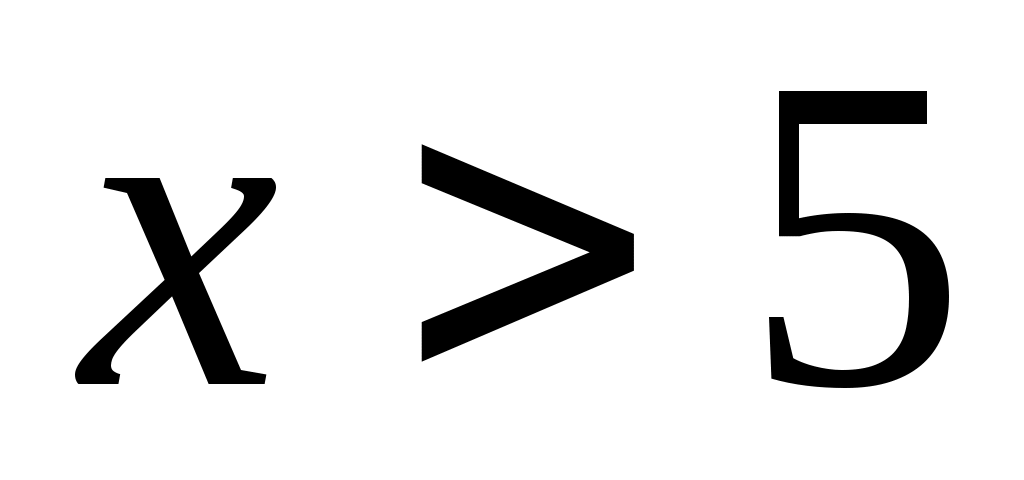

Раскрыть скобки
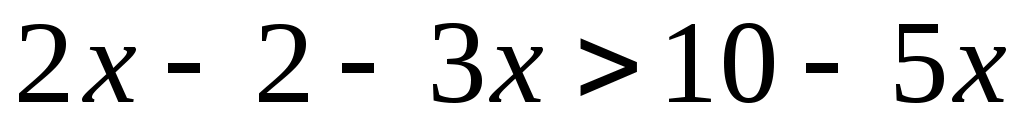
Переносим слаг. с х в лев. часть, а без х в прав.
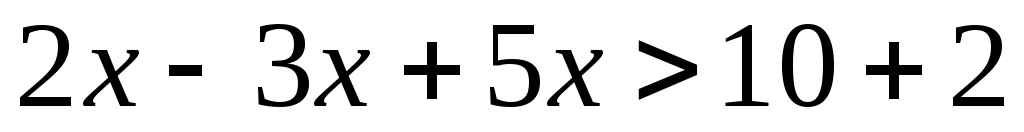
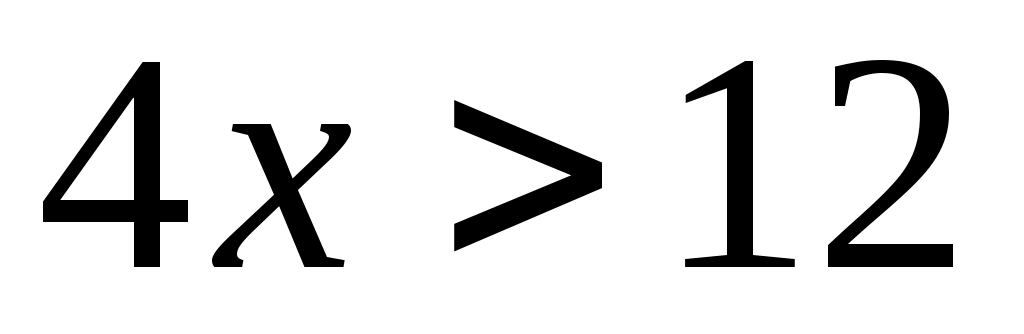 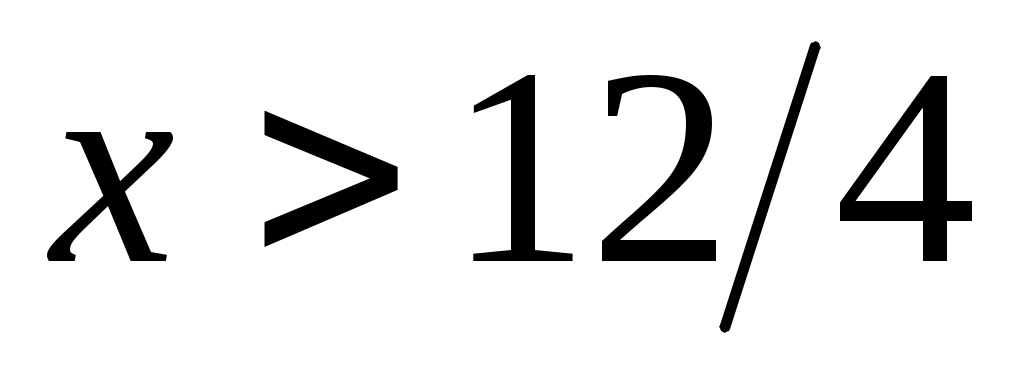 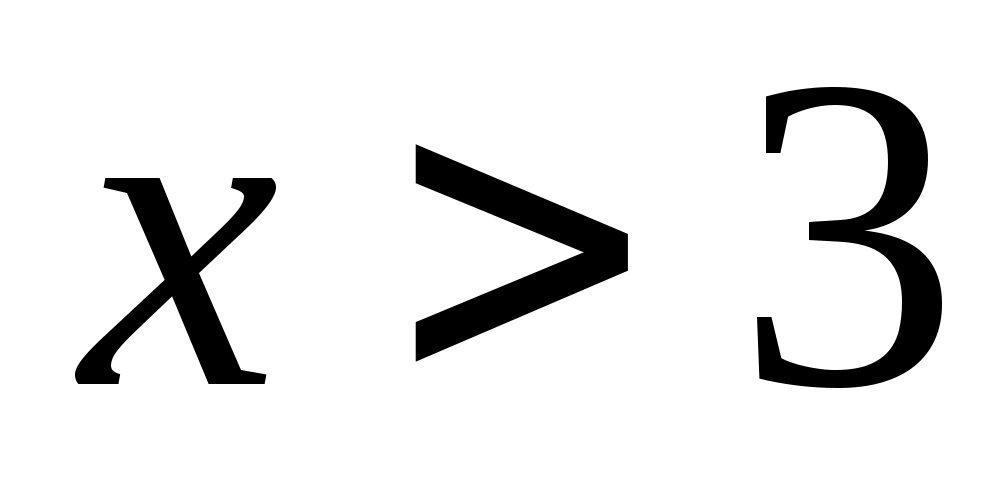

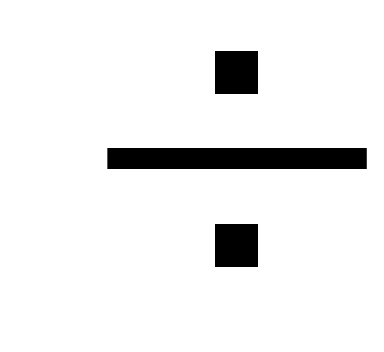

с обратным знаком
-25 x<125
-25x-125<0
Так как -25<0, то меняем знак
>
>
арточка №2. Инструкция
|
К 
Образец:
12-4(3-2х)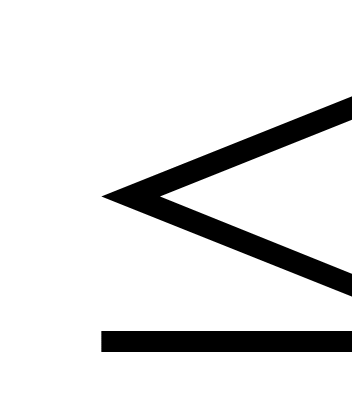 3(5+х) 3(5+х)
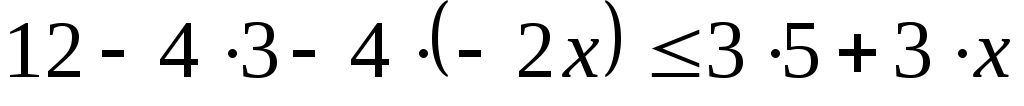
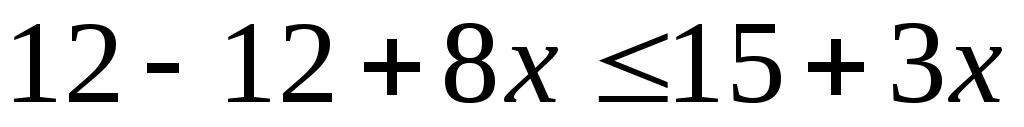
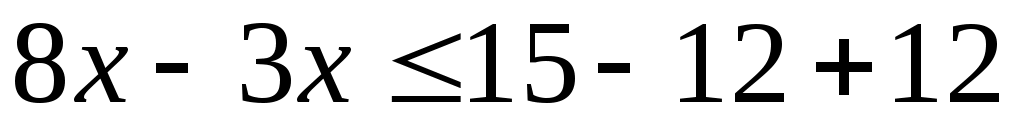
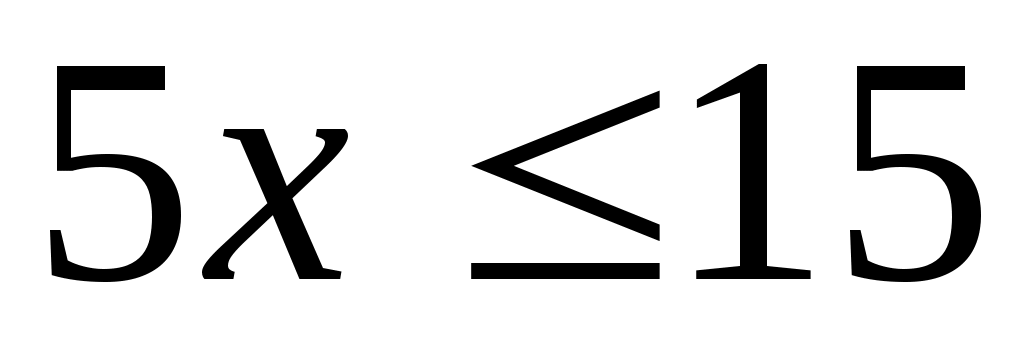

Реши уравнение и сравни результат с ответом
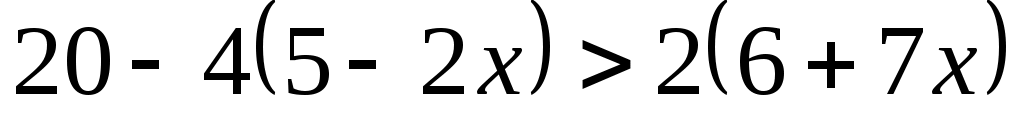 Отв. Отв. 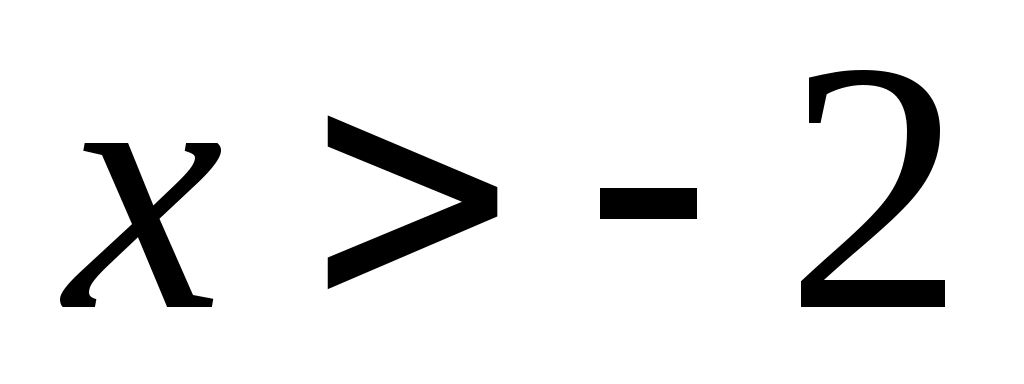
арточка №3. Выполни по образцу
3
 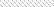
Х

|
К
Решите неравенство:
а) 6х – 18;
б) – 4х > 36;
в) 0,5(х – 2) + 1,5х < х + 1
г) 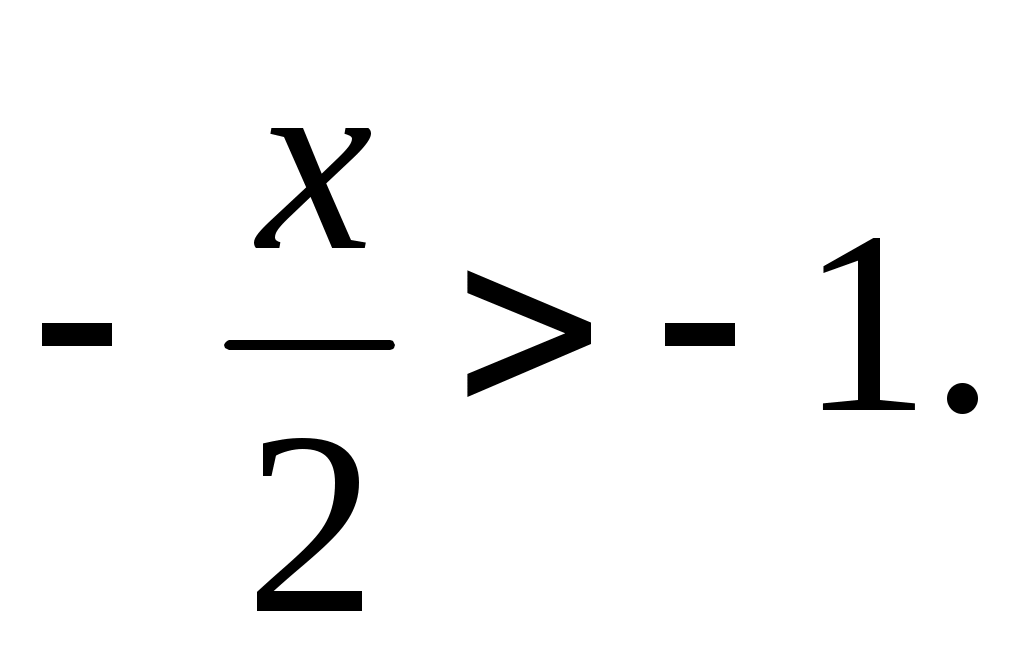
арточка №4. Реши самостоятельно
|
К  арточка №5. Проверь себя арточка №5. Проверь себя
Решите неравенство:
а) 5х > – 45;
б) – 6х 42;
в) 1,2(х + 5) + 1,8х > 7 + 2х
Отв. а) x>-9 б) x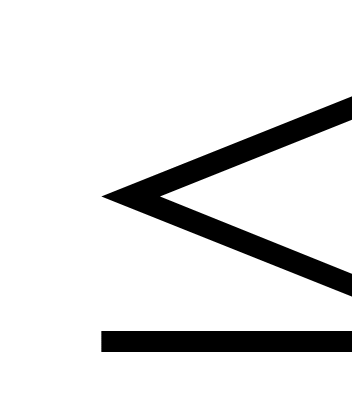 -7 в) x>1 -7 в) x>1
|
К
Решите неравенство
12х+7 > 14х + 5.
13х+8 < 15х + 4.
6+8х>5х-3.
6-6х>-12-8х
7х+5<4х-7.
арточка №6. Контрольная работа
|
К
Эскиз графика
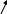 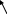 арточка №1. Справка арточка №1. Справка
Квадратные неравенства
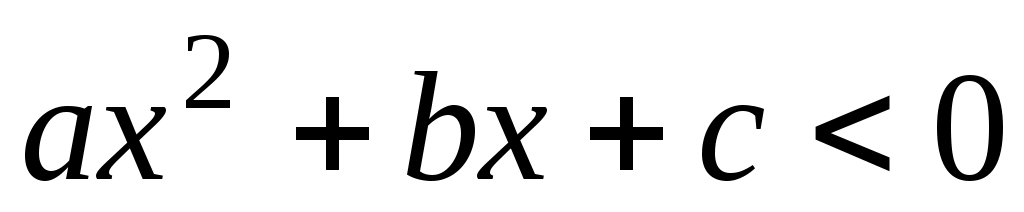
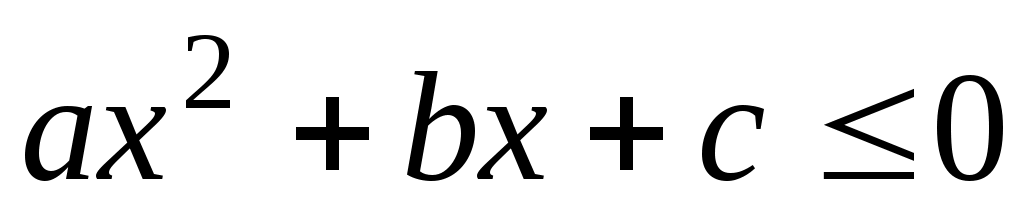
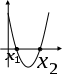 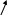  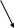 
Выше 0Х
Ниже ОХ
|
К
>
Приравнять квадратный трехчлен к нулю.
Найти дискриминант и сравнить с нулем
Найти корни уравнения (если есть)
Изобразить эскиз параболы:
Определить направление ветвей
(а>0, ветви вверх
a<0 ветви вниз)
Отметить точки пересечения с ОХ (если есть корни)
Схематично нарисовать параболу
По эскизу определить нужные значения х
арточка №2. Инструкция
|
К 
Образец: 2х2 – 13х + 6 < 0;
2х2 – 13х + 6 = 0;
D = 169 – 48 = 121>0;
х1 =  , х2 = , х2 = = 6 = 6
у = 2х2 – 13х + 6.Ветви параболы напр. вверх.
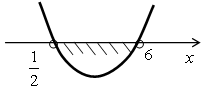 О т в е т: О т в е т:  . .
Реши и сравни с ответом
2х2 + 5х – 7 < 0;
Отв. (–3,5; 1).
арточка №3. Выполни по образцу

|
К
Решите неравенство:
х2 + 2х – 15 < 0;
10 – 3х2 ≤ 5х – 2;
(3х – 2)2 – 4х (2х – 3) > 0
арточка №4. Реши самостоятельно
|
К  арточка №5. Проверь себя арточка №5. Проверь себя
Решите неравенство:
а) 2х2 – х – 15 > 0;
б) х2 – 25 > 0;
в) 5х2 – 4х + 21 > 0.
Отв.
а) (–∞;–2,5)  (3; +∞). (3; +∞).
б) (–∞; –5)  (5; +∞) (5; +∞)
в) (–∞; +∞)
|
К
Решите неравенство
а) 5х2 + 3х – 8 > 0;
б) х2 – 9 > 0;
в) 3х2 – 6х + 32 > 0.
арточка №6. Контрольная работа
|
К арточка №1. Справка арточка №1. Справка
Метод интервалов
Решить неравенство
(х + 2) (х – 2) (х + 1) > 0;
Решаем уравнение
(х + 2) (х – 2) (х + 1) =0;
х1 = –2, х2 = 2, х3 = –1.
Наносим корни уравнения на числовую прямую, разбивая ее на промежутки. Определяем знак левой части неравенства на каждом промежутке
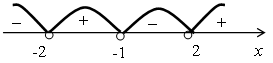
Выбираем ответ х  (–2; –1) (–2; –1)  (2; +∞). (2; +∞).
|
К
>
Преобразовать неравенство, чтобы в правой части остался ноль.
Разложить левую часть на множители (для дробных неравенств - разложить на множители числитель и знаменатель дроби)
Приравнять левую часть к нулю и найти корни (для дробных – еще определить при каких х знаменатель равен нулю)
Нанести найденные числа на прямую
Определить знак лев. части на каждом промежутке
Выбрать ответ
арточка №2. Инструкция
|
К 
Образец:
(х – 6) (х + 5) (х + 8) < 0
(х – 6) (х + 5) (х + 8) =0
х1 = 6, х2 = –5, х3 = –8.

х  (–∞; –8) (–∞; –8)  (–5; 6) (–5; 6)
Реши и сравни с ответом
(4 – х) (х – 2) ≤ 0; х  (–∞; 2) (–∞; 2)  (4; +∞). (4; +∞).
–(х – 3) (х + 5) > 0; х  (-5;3) (-5;3)
арточка №3. Выполни по образцу

|
К
Решите неравенство:
(х + 6) (х + 2) (3х – 1) > 0;
(х + 8) (5х + 4) (1 – 2x) > 0;
х2 + 4х – 5 < 0;
х 2x. 2x.
арточка №4. Реши самостоятельно
|
К  арточка №5. Проверь себя арточка №5. Проверь себя
Решите неравенство:
а) (х – 3) (х2 – 3х + 2) > 0.
б) (х2 – 1) (х – 2) (х + 3) ≤ 0.
в) (х2 – 3х – 4) (х2 + х – 2) < 0.
Отв. а) (0; 2)  (2; 3). (2; 3).
б) [–3; –1]  [1; 2]. [1; 2].
в) (–2; –1)  (1; 4). (1; 4).
|
К
Решите неравенство
а) (х + 6) (х + 2) (3х – 1) > 0;
б) (х + 8) (5х + 4) (1 – 2x) > 0;
в) (х + 6) (х + 2) (3х – 1) > 0;
г) (х + 8) (5х + 4) (1 – 2x) > 0;
д) 16 – 40x + 25х2 > 0.
арточка №6. Контрольная работа
|
К арточка №1. Справка арточка №1. Справка
Метод интервалов
Решить неравенство
(х + 2) (х – 2) (х + 1) > 0;
Решаем уравнение
(х + 2) (х – 2) (х + 1) =0;
х1 = –2, х2 = 2, х3 = –1.
Наносим корни уравнения на числовую прямую, разбивая ее на промежутки. Определяем знак левой части неравенства на каждом промежутке

Выбираем ответ х  (–2; –1) (–2; –1)  (2; +∞). (2; +∞).
|
К
>
Преобразовать неравенство, чтобы в правой части остался ноль.
Разложить левую часть на множители (для дробных неравенств - разложить на множители числитель и знаменатель дроби)
Приравнять левую часть к нулю и найти корни (для дробных – еще определить при каких х знаменатель равен нулю)
Нанести найденные числа на прямую
Определить знак лев. части на каждом промежутке
Выбрать ответ
арточка №2. Инструкция
|
К 
Образец:
 > 0; > 0;  < 0. < 0.

О т в е т: (–∞; –1)  (2; 4). (2; 4).
Реши и сравни с ответом
 ≥ 0. О т в : (–2; 1) ≥ 0. О т в : (–2; 1)  [2; 3]. [2; 3].
арточка №3. Выполни по образцу

|
К
Решите неравенство:
в) < 0;
г) 
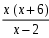
0
арточка №4. Реши самостоятельно
|
К  арточка №5. Проверь себя арточка №5. Проверь себя
Решите неравенство:
 ≤ 0 ≤ 0
 ≥ 0 ≥ 0
 ≤ 0 ≤ 0
Отв. а) (–∞; –1)  [0; 2] [0; 2]
б) (–∞; –3)  [–2; 2) [–2; 2)
в) (–∞; –6]  (–1; 1,5) (–1; 1,5)
|
К
Решите неравенство


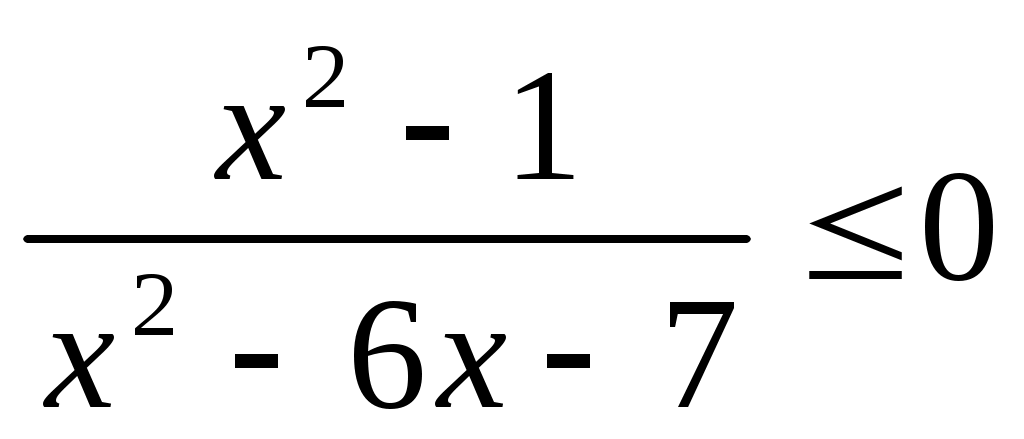
арточка №6. Контрольная работа
0
<0
| |
|
|
 Скачать 199 Kb.
Скачать 199 Kb.