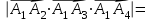Витте Математика Вариант 4. РР1 математика_Вар-4. Кафедра Математика и информатика
 Скачать 245.45 Kb. Скачать 245.45 Kb.
|
 Кафедра ___Математика и информатика_________________________ Рейтинговая работа _______________________________________________ (домашняя творческая работа, расчетно-аналитическое задание, реферат, контрольная работа) по дисциплине _________________________________________________ Задание/вариант № ____________ Тема* ______________________________________________________________ Выполнена обучающимся группы __________ __________________________________________________________________ (фамилия, имя, отчество) Преподаватель ____________________________________________________ (фамилия, имя, отчество) Москва – 201__ г. * при наличии Вариант 4 1) Даны матрицы 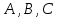 и число и число 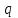 . Найти матрицу . Найти матрицу 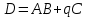 . .4). 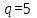 , , 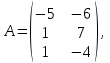 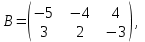 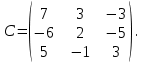 Решение: Произведением А 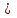 В матрицы размера m В матрицы размера m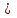 n и матрицы размера n n и матрицы размера n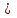 р является матрица размера m р является матрица размера m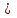 p , элементы dij которой равняются сумме произведений элементов і-й строки матрицы А на соответствующие элементы j-го столбца матрицы В : p , элементы dij которой равняются сумме произведений элементов і-й строки матрицы А на соответствующие элементы j-го столбца матрицы В :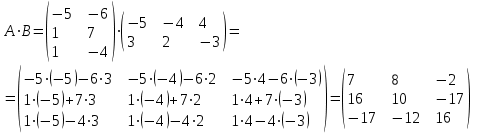 Произведением матрицы на число является матрица, элементы которой равняются произведениям элементов матрицы и числа, то есть: 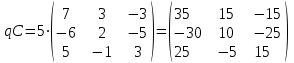 Алгебраической суммой (разностью) матриц одинакового размера m 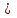 n является матрица размера m n является матрица размера m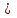 n, элементы которой равняются алгебраической сумме (разности) соответствующих элементов данных матриц: n, элементы которой равняются алгебраической сумме (разности) соответствующих элементов данных матриц: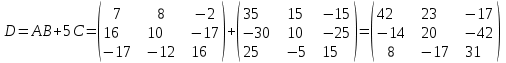 . .Ответ: 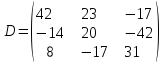 . .2) Дана система линейных алгебраических уравнений Найти решение этой системы любым методом. 4). 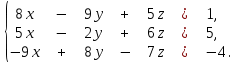 Решение: Решаем эту систему линейных уравнений методом Крамера. Формулы Крамера: 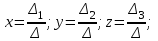 где где 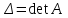 - определитель матрицы системы, - определитель матрицы системы, 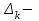 это вспомогательный определитель, который получаем из основного определителя это вспомогательный определитель, который получаем из основного определителя 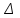 путем замены его k-го столбца на столбец свободных членов системы. Вычислим все эти определители с помощью разложения по элементам 1-й строки: путем замены его k-го столбца на столбец свободных членов системы. Вычислим все эти определители с помощью разложения по элементам 1-й строки:
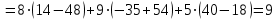
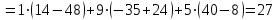
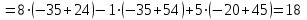
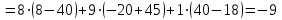 Тогда по формулам Крамера: 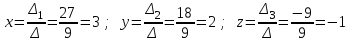 Ответ: 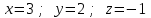 . .3) Известны координаты (см. таблицу 1) в прямоугольной системе координат 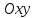 трех точек трех точек 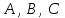 , являющихся вершинами треугольника. Изобразить треугольник , являющихся вершинами треугольника. Изобразить треугольник 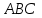 в этой прямоугольной системе координат и найти: в этой прямоугольной системе координат и найти:3.1 координаты векторов 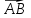 , , 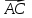 и их длины; и их длины;3.2 скалярное произведение векторов 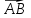 , , 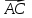 и угол и угол 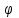 между векторами между векторами 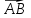 , , 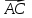 ; ;3.3 векторное произведение векторов 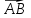 , , 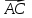 и площадь треугольника и площадь треугольника 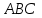 3.4 значение параметра 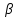 , при котором векторы , при котором векторы 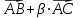 и и 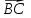 будут коллинеарны; будут коллинеарны;3.5 координаты точки 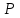 , делящей отрезок , делящей отрезок 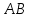 в отношении в отношении 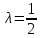 ; ;3.6 каноническое уравнение стороны 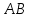 ; ;3.7 уравнение с угловым коэффициентом и угловой коэффициент прямой, проходящей через точку 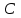 параллельно прямой параллельно прямой 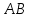 . .Таблица 1
Решение: 3.1. найдем координаты векторов 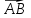 , , 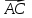 и их длины. и их длины.Координаты и длина 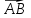 : :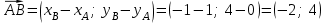 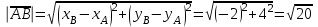 Координаты и длина 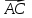 : :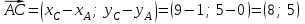 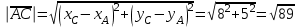    L 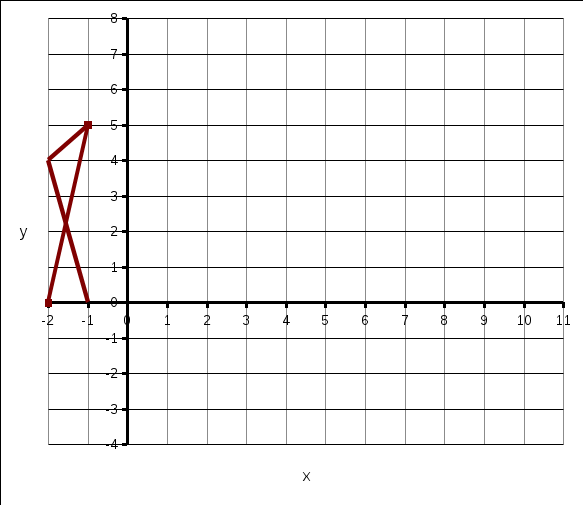 3.2 Найдем скалярное произведение векторов 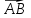 , , 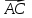 и угол и угол 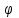 между векторами между векторами 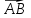 , , 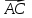 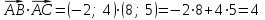 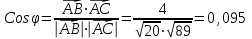 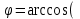 0,095) ≈ 84,6. 0,095) ≈ 84,6.3.3 найдем векторное произведение векторов 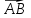 , , 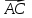 и площадь треугольника и площадь треугольника 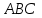 Векторным произведением вектора a на вектор b называется вектор c, длина которого численно равна площади параллелограмма построенного на векторах a и b, перпендикулярный к плоскости этих векторов. Треугольник 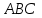 построен на векторах построен на векторах 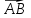 и и 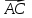 Его площадь равняется половине площади параллелограмма, построенного на этих векторах, которая, в свою очередь равняется модулю векторного произведения этих векторов: 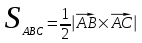 . .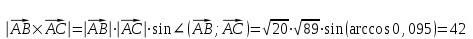 Тогда площадь 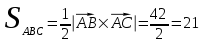 . .3.4 найдем значение параметра 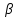 , при котором векторы , при котором векторы 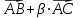 и и 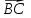 будут коллинеарны. будут коллинеарны.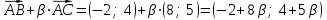 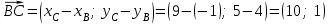 Векторы будут коллинеарны, если их координаты пропорциональны: 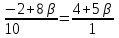 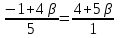 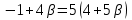 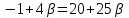 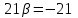 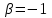 . .3.5 найдем координаты точки 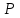 , делящей отрезок , делящей отрезок 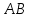 в отношении в отношении 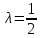 , если , если 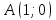 , , 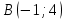 , т.е. , т.е. 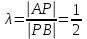 . .Координаты точки 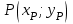 , которая делит отрезок АВ в отношении , которая делит отрезок АВ в отношении 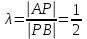 , выражаются формулами: , выражаются формулами: 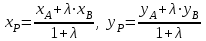 , т.е. , т.е.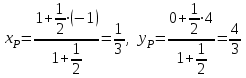 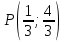 . .3.6 найдем каноническое уравнение стороны 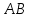 . .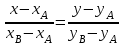 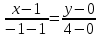 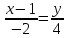 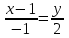 - это каноническое уравнение. - это каноническое уравнение. 3.7 найдем уравнение с угловым коэффициентом и угловой коэффициент прямой, проходящей через точку 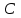 параллельно прямой параллельно прямой 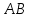 . .Сначала составим уравнение с угловым коэффициентом прямой АВ, если каноническое уравнение имеет вид 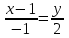 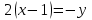 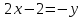 уравнение с угловым коэффициентом : уравнение с угловым коэффициентом : 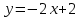 Прямая L, параллельная прямой АВ, имеет тот же угловой коэффициент, что и прямая АВ, т.е. уравнение с угловым коэффициентом 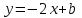 . Константу b находим из условия, что искомая сторона проходит через точку С(9; 5), т.е. при х = 9: у = 5. Подставляем эти координаты в уравнение: . Константу b находим из условия, что искомая сторона проходит через точку С(9; 5), т.е. при х = 9: у = 5. Подставляем эти координаты в уравнение: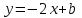 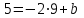 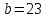 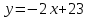 . .Угловой коэффициент k = -2. 4) Известны координаты (см. таблицу 2) в прямоугольной системе координат  вершин пирамиды вершин пирамиды 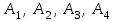 . .4.1 найти смешанное произведение векторов 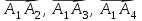 и объем пирамиды и объем пирамиды 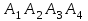 ; ;4.2 найти каноническое уравнение прямой 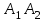 ; ;4.3 найти общее уравнение плоскости 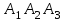 . .Таблица 2
Решение: 4.1. Координаты вектора А1А2:
Координаты вектора А1А3 :
Координаты вектора А1А4 :
Объем пирамидыравняется 1/6 от объема параллелепипеда, построенного на векторах 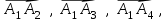 который, в свою очередь равняется модулю смешанного произведения этих трех векторов. который, в свою очередь равняется модулю смешанного произведения этих трех векторов.Находим смешанное произведение этих векторов:
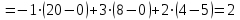 То есть объем пирамиды : V = 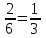 (ед3). (ед3).4.2 найдем каноническое уравнение прямой 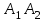 . .Уравнение прямой A1A2 : 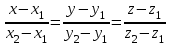 , где A1(2,4,3), A2(1,1,5) , где A1(2,4,3), A2(1,1,5) 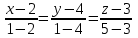 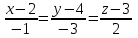 . .4.3. Уравнение плоскости 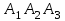 : : 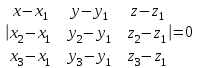
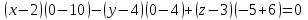 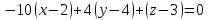 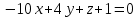 . .Это искомое уравнение плоскости. Литература 1. Ильин В.А., Позняк Э.Г., Аналитическая геометрия, М., Наука, 1988. 2. Беклемишев Д.В., Курс аналитической геометрии и линейной алгебры, М, Наука, 1984. 3. Канатников А.Н., Крищенко А.П., Аналитическая геометрия, М., Изд. МГТУ им. Н.Э. Баумана, 1999. 4. Бахвалов С.В., Моденов П.С., Пархоменко А.С., Сборник задач по аналитической геометрии, М., Наука, 1976. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

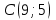
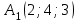
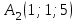
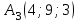
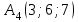
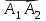 =(
=(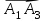 =(
=(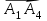 =(
=(