теория игр. ROS матан. Кафедра менеджмента и бизнеса Применение теории игр как экономикоматематического метода для решения экономических задач Выполнили, специальность
 Скачать 51.02 Kb. Скачать 51.02 Kb.
|
|
кафедра менеджмента и бизнеса Применение теории игр как экономико-математического метода для решения экономических задач Выполнили:, специальность , Содержание: 1. Определение сферы использования и описание теоретических основ экономико-математического метода…………………………………………….3 1.1 Минимаксный критерий……………………………………………………...5 1.2 Критерий Лапласа…………………………………………………………….5 1.3 Критерий Сэвиджа…………………………………………………................5 2. Применение метода теории игр на примере задачи выбора производственного решения……………………………………………………..7 2.1 Поиск решения с помощью минимаксного критерия……………………....7 2.2 Поиск решения с помощью критерия Байеса – Лапласа…………………………………………………………………………….7 2.3 Поиск решения с помощью критерия Сэвиджа……………………………………………………………………………8 Заключение………………………………………………………………………...9 1. Определение сферы использования и описание теоретических основ экономико-математического метода Теория игр рассматривает наилучшие стратегии для предприятий. Стратегии подбираются под ситуации, которые относятся к выбору положительных производственных решений системы научных и хозяйственных экспериментов, с созданием статистического контроля, хозяйственных взаимоотношений между предприятиями промышленности и других отраслей. Если конфликтным ситуациям придавать форму математической задачи, то их можно интерпретировать, как игру двух или более игроков, где задача каждого игрока максимально увеличить свою выгоду, используя средства остальных. Это является причиной использования именно теории игр в поиске производственно-хозяйственных решений. Для решения подобных задач обязательно составление четкой формулировки условий: установления количества игроков и правил игры, рассмотрения возможных стратегий игроков, возможных выигрышей, а также проигрышей. Главенствующую часть в условии задачи занимает стратегия, т.е. совокупность правил, определяющих выбор действия игрока в той или иной ситуации. Каждый игрок выбирает для себя свое количество стратегий, которое может варьироваться от одного до бесконечности, в зависимости от этого игры могут так же иметь конец и быть бесконечными. Если игра считается конечной, то для нее создаются матрицы выигрышей, а если игра бесконечная, то для нее создаются функции выигрышей. Для предприятий промышленного типа теория игр используется для нахождения оптимальных решений, к примеру, для определения оптимального количества материалов, запасов сырья, полуфабрикатов, а также в различных экономических ситуациях, например, в выборе качества сырья. В первом случае сравниваются две направленности выбора: увеличения запасов, в том числе и страховых, которые будут обеспечивать постоянную работу производства; сокращения запасов, которые будут требовать меньше затрат на их хранение и поддержку качества; во втором случае желание выпускать большее количество продукции, которое ведет к уменьшению трудовых затрат; к улучшению качества, которое часто влечет за собой уменьшение количества продукции, а также увеличение трудовых затрат. Например, в машиностроительном производстве сталкиваются два направления: первое, где преследуется цель затрачивания малого количества металла в изделии конструкции, и второе, где целью является повышение безопасности конструкции. Очень часто природные условия становятся главным фактором, влияющим на эффективность работы предприятий промышленного типа. Такие условия называются условиями неопределенности. Для выбора решения в условиях неопределенности данные обычно назначаются в виде матрицы, где значения в строках являются возможными действиям, а столбцы – возможными состояниями системы. Пример: Пусть мы имеем определенный материал, из которого нужно изготовить изделие, но износоустойчивость мы не можем определить при допустимых затратах, а известны только нагрузки. Необходимо найти объем, который должно иметь изделие, изготовленное из данного материала. Варианты решения таковы: Е1 – выбор объема для большей износоустойчивости; Еm – выбор объема для меньшей износоустойчивости; Ei – промежуточные решения. Условия требующие рассмотрения таковы: F1 – условия, которые помогают получить максимальную износоустойчивость; Fn – условия, которые помогают получить минимальную износоустойчивость; Fi – промежуточные условия. eij = е(Ei ; Fj) – по этому результату можно понять оценку, соответствующую варианту Ei условиям Fj характеризующие прибыль, полезность или надёжность. Тогда семейство (матрица) решений
Для нахождения однозначного и по мере возможности самого выгодного решения нужно ввести оценочную (целевую) функцию. При этом матрица решений При выявлении наилучших решений, беря во внимание особенность игр, используют различные критерии, которые помогают в принятии решения, давая некие логические схемы. Критерии дают возможность рассмотреть решение с разных сторон, тем самым они помогают обходить критические ошибки в хозяйственной деятельности. 1. 1 Минимаксный критерий Правило нахождения решения, которое будет соответствовать минимаксному критерию (ММ-критерию), объясняется следующим образом: Минимальные результаты каждой строки идут в дополнение к матрице решений в виде дополнительного столбца. Далее смотрим наибольшее значение в этом столбце и выбираем соответствующие строки вариантов. Такой способ выбора позволяет полностью избежать рисков, т.е. тот, кто принимает решение, не столкнется с проигрышным результатом. Таким образом ММ-критерий можно считать самым надежным. Применять ММ-критерий следует только в определенной ситуации, которая соответствует одному из следующих: 1. О возможности появления внешних состояний Fj ничего не известно; 2. Приходится считаться с появлением различных внешних состояний Fj; 1.2 Критерий Лапласа Если игрок не имеет точной информации о априорных вероятностях природных условий, то приемлемой стратегией будет та, что обеспечит наибольший средний выигрыш 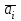 игрока при условии равенства всех вероятностей игрока при условии равенства всех вероятностей 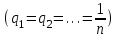 . Это и есть принцип недостаточного основания Лапласа. . Это и есть принцип недостаточного основания Лапласа.В этом случае к матрице решений 1.3 Критерий Сэвиджа 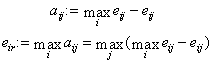 aij представляется как максимальный дополнительный выигрыш, а он получает если при условии Fj заменить вариант Ei на какой-либо другой, подходящий для этого условия. Так же величину aij допустимо трактовать как потери (штрафы), которые появляются при условии Fj, когда заменяется подходящий для него вариант на вариант Ei. Во втором варианте представлены максимально возможные (по всем внешним состояниям Fj, j= Правило, подходящее под критерий Сэвиджа можно теперь интерпретировать так: 1) От самого большого результата max 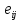 соответствующего столбца отнимается каждый элемент матрицы решений соответствующего столбца отнимается каждый элемент матрицы решений 2) Из разности aij образуется матрица остатков Данные критерии дают понять, что из-за того, что их исходные позиции достаточно жесткие, их можно применить исключительно для приближенных к идеалу практических решений. Так же возможно одновременное поочередное применение разных критериев, но такое подходит под случай, когда вероятна достаточно сильная идеализация. Затем выбирается конечное решение из нескольких допустимых вариантов. Данный метод дает возможность погрузиться вглубь всех связей проблем с выбором решений, а также уменьшает воздействие субъективных факторов. 2. Применение метода теории игр на примере задачи выбора производственного решения При открытии любого предприятия самым первым и самым важным вопросом является, что производить. После того, как будет определено направление продукции и ассортимент, следует подсчитать с помощью теории игр на основе статистики или на основе информации предприятий, которые уже присутствуют на рынке, какой вид продукта будет самым прибыльным из возможных. Например, предприятию, которое занимается производством кроссовок, нужно принять решение, из какого материала производить кроссовки (натуральная кожа, синтетическая кожа, сеточный материал), в зависимости от погодных условий, будет ли погода дождливая или умеренная. Далее представлены примерные доходы при двух исходах, в млн. тенге:
Нужно принять решение относительно того, в какое направление вложить деньги, чтобы оно принесло максимальную прибыль. 2.1 Поиск решения с помощью минимаксного критерия Составляется платежная матрица:
Из которой следует, что нижняя чистая цена игры 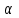 = max = max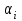 = 1,5, а верхняя - = 1,5, а верхняя - 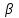 = min = min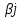 = 1. Следовательно, мы видим, что α ≠ β, а это значит, что нет точки равновесия. Далее если следовать ММ-критерию, то необходимо провести полную проверку, так как платежную матрицу не сделать проще, потому что в ней нет стратегии, которая бы доминировала над остальными. Так как мы ведем игру, в которой предприятие зависит от природных условий, мы не можем исключать те или иные погодные условия, потому что это контролировать невозможно. = 1. Следовательно, мы видим, что α ≠ β, а это значит, что нет точки равновесия. Далее если следовать ММ-критерию, то необходимо провести полную проверку, так как платежную матрицу не сделать проще, потому что в ней нет стратегии, которая бы доминировала над остальными. Так как мы ведем игру, в которой предприятие зависит от природных условий, мы не можем исключать те или иные погодные условия, потому что это контролировать невозможно.2.2 Критерий Байеса – Лапласа Так как в задаче вероятность дождливой погоды и умеренной равны, то мы имеем 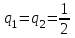 . Средние выигрыши помещены в столбце . Средние выигрыши помещены в столбце 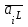 . .
Чистая стратегия Е2 по Байесу-Лапласу оказывается самой наилучшей. Так же для полной объективности можно рассмотреть среднее значение вероятностей 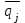 , которые будут определены специалистами, основывающимися на собственном опыте. , которые будут определены специалистами, основывающимися на собственном опыте.Из этого следует, что критерий Байеса-Лапласа оптимистичнее ММ-критерия, но он подразумевает под собой обладание большей информации и довольно-таки продолжительную реализацию. 2.3 Критерий Сэвиджа Так как природа может создать любые условия, то определить наверняка ничего невозможно, поэтому мы переходим к матрице рисков, которая показывает преимущества одних стратегий над другими.
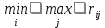 = = 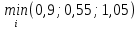 = 0,55 = 0,55 В данном случае оптимальной будет стратегия Е2, в которой наименьшая величина риска. Из выше указанных критериев мы можем сделать вывод, что самым прибыльным вариантом производства является производство кроссовок из натуральной кожи, вне зависимости от погодных условий. Заключение: Теория игр является одним из разделов исследования операций и представляет собой теорию математических моделей, которая позволяет выбирать наилучшее решение в различных ситуациях. Она построена на исследовании ситуаций, в которых главной целью является выбор самого выгодного решения для производственной, организационной, хозяйственной и различных других проблем предприятий. Актуальность данного метода растет в соответствии с развитием предпринимательства, так как метод является очень практичным. Применение теории игр в таких областях как экономика и социальные науки за последние несколько лет значительно возросло. Например, в экономике она нашла широкое применение в решении общехозяйственных задач, проблем стратегического назначения, а также решение в организационной структуре и систем форсирования предприятий. В своей работе мы представили пример применения теории игр, где мы смогли рассчитать производство какого из видов продукции, принесет больше всего прибыли, в условии неопределенности. Таким образом мы наглядно показали применение теории игр как экономико-математического метода для решения экономической задачи. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||