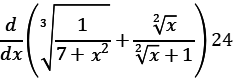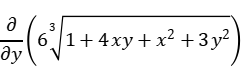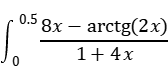Кафедра сау отчет по лабораторной работе 4 по дисциплине Математические пакеты в инженернотехнических расчетах тема основы символьных вычислений и операций над полиномами Вариант 8 Студент гр. 9498 Тао Сяовэй
 Скачать 395.52 Kb. Скачать 395.52 Kb.
|
|
МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) Кафедра САУ ОТЧЕТ по лабораторной работе № 4 по дисциплине «Математические пакеты в инженерно-технических расчетах»ТЕМА: основы символьных вычислений и операций над полиномамиВариант 8 Студент гр. 9498 Тао Сяовэй Преподаватель Илатовская Екатерина Вадимовна. Санкт-Петербург 2023 г. Цель работы: получение навыков работы с символьными вычислениями и операциями с полиномами в MATLAB. 4.1. Основные сведенияSymbolic Math Toolbox позволяет пользоваться символьной математикой и вычислениями с плавающей точкой в MATLAB. Пакет включает вычислительное ядро пакета Maple V, разработанного фирмой «Waterloo Maple Software». Extended Symbolic Math Toolbox предоставляет пользователю дополнительную возможность программирования на Maple и обеспечивает доступ к специализированным библиотекам Maple. 4.2. Программа работы4.2.1. Символьные вычисления1. Создание символьных переменных и массивов возможно двумя способами: c помощью команды sym (x = sym('x'); y = sym('y'); z = sym('z')) и с помощью команды syms (syms a b c). Создайте символьную матрицу 3 × 3 и вычислите ее определитель. Создайте символьную диагональную матрицу и вычислите ее след. Код: clc syms a b c d A=[1 a b 4;d c 12 3;a 3 5 6;b 3 4 5] det(A) Результаты бега: A = [1, a, b, 4] [d, c, 12, 3] [a, 3, 5, 6] [b, 3, 4, 5] ans = 144*b - 144*a + c + 12*d - 48*a*b + 16*a*c - a*d - 20*b*c - 3*b*d + 6*b^2*c + 48*a^2 - 9*b^2 - 5*a*b*c + 27 2. Существует возможность графического построения символьных функций – команда ezplot. Пример: % Область определения по умолчанию от –2*pi до 2*pi >> syms t % определение символьной переменной >> f1= sin(t); >> ezplot(f1), grid Код: syms x; X=1:0.05:10; y=sin(x); ezplot(y),grid Результаты бега: 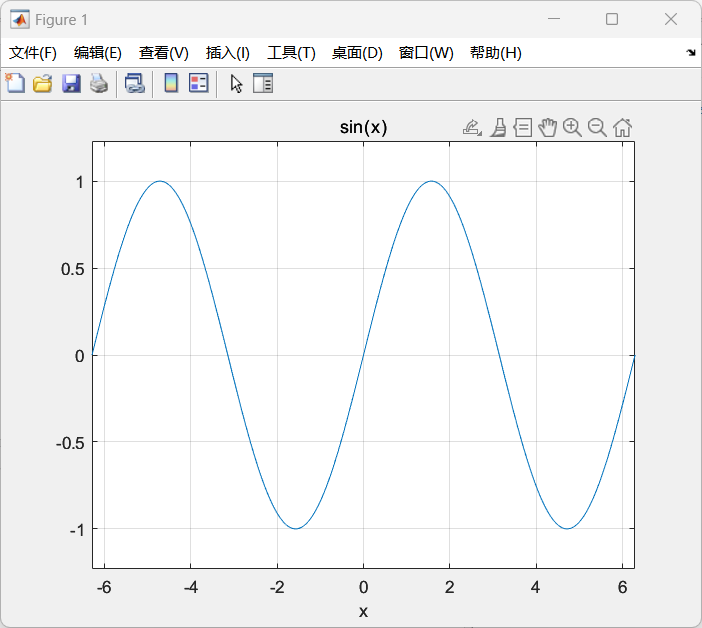 Рис 1 Результаты 3. Для решения символьных конечных уравнений предназначена функция solve. Пример: >> syms x % задание символьной переменной х >> solve('x^2+2*x–8=0') % решение квадратного уравнения >> solve('x–sin(x)–0.25=0') % решение нелинейного уравнения При решении системы уравнений аргументы функции solve увеличиваются в соответствии с числом этих уравнений. Например: >> syms x1, x 2 >> [X1,X2]=solve('x1+3*log(x1)-x2^2=0,2*x1-x1*x2-5*x1+1=0'); >> simplify([X2,X1]) % для упрощения результата Код: syms x0; solve(7*x0^3+x0^2-28*x0-4==0,x0) syms x y; [x,y]=solve(x^2+y^2-17==0,x*y+4==0); simplify([x,y]) Результаты бега: ans = -2 -1/7 2 ans = [ 1, -4] [ 4, -1] [-4, 1] [-1, 4] 4. Другими типовыми функциями вычислений над символьными переменными являются: вычисления предела – функция limit (табл. 4.1); дифференцирование функций одной переменной — функция diff; интегрирование функции одной переменной — функция int. Таблица 4.1
Вычислите Для нахождения n-й производной функции f(x) по переменной h необходимо записать: diff(f(x),h,n). Вычислите Вычисление неопределенного интеграла функции f(x) по переменной h: int(f(x),h). Вычисление определенного интеграла функции f(x) по переменной h в пределах от a до b: int(f(x),h,a,b). Вычислите Код: syms x; y=(x+3)^2/x; int(y,x) int(y,x,1,8) Результаты бега: ans = 6*x + 9*log(x) + x^2/2 ans = 27*log(2) + 147/2 4.2.2. Операции с полиномами1. Представление полинома р(х) = аn хn + an−1 xn−1+ ... + а2 x2 + а1 х + а0 в MATLAB осуществляется следующим образом: p=[ аn an-1... а2 а1 а0]. Также возможно построение многочлена по заданным корням (при помощи функции poly). Создайте два полинома пятой степени двумя способами. Для символьного отображения полинома по вектору заданных коэффициентов служит команда poly2sym: >> c=[1 2 3 4 5]; >> poly2sym(c) % вектор коэффициентов может быть непосредственно введен в poly2sym: ans = 1*x^4+2*x^3+3*x^2+4*x+5. Код: p=[2 3 0 16 24]; poly2sym(p) Результаты бега: ans = 2*x^4 + 3*x^3 + 16*x + 24 Умножение и деление полиномов осуществляются при помощи функций conv и dconv соответственно. Произведите обе эти операции над созданными полиномами. Для помощи по синтаксису функций используйте команду help. Код: p=[2 3 0 16 24]; roots(p) q=[2 0 1]; conv(p,q) deconv(p,q) Результаты бега: ans = 1.0000 + 1.7321i 1.0000 - 1.7321i -2.0000 + 0.0000i -1.5000 + 0.0000i ans = 4 6 2 35 48 16 24 ans = 1.0000 1.5000 -0.5000 3. Приближение данных полиномом осуществляется с использованием функции polyfit(x, y, n), где x и y – это заданные значения аргумента и функции, n – порядок полинома. Выполните приведенный пример приближения данных полиномом третьего порядка: >> x=1:7; % заданный аргумент >> y=[15, 10, 2, 47, 23, 78, 10]; % заданная функция >> p=polyfit(x,y,3); % формирование полинома >> x2=1:0.1:7; % точки для построения полинома >> y2=polyval(p,x2); % вычисление значений функции >> plot(x,y,x2,y2) % построение результата Код: x=1:7; y=[15, 10, 2, 47, 23, 78, 10]; p=polyfit(x,y,3); x2=1:0.1:7; y2=polyval(p,x2); plot(x,y,x2,y2) Результаты бега: 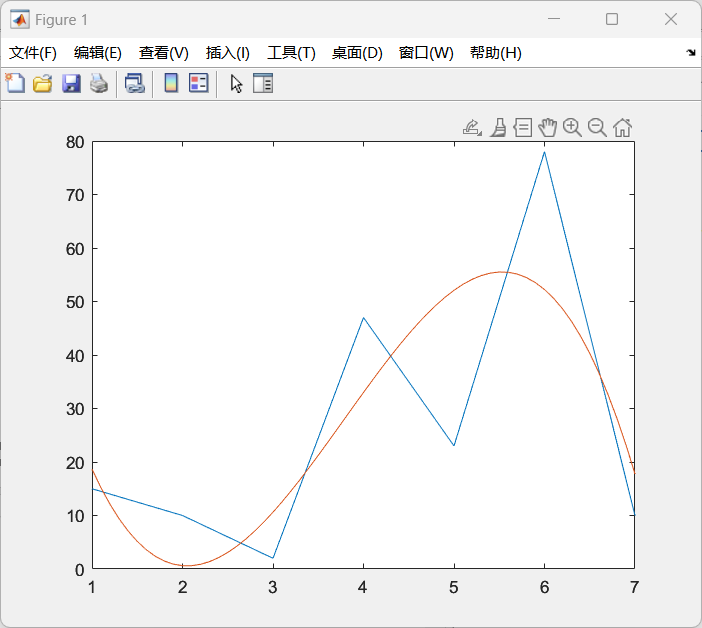 Рис 2 Результаты 4.2.3. Задание на самостоятельную работу1. Вычислите в соответствии с вариантом:
Код: syms y x a=6^2*sqrt(1+4*x*y+x^2+3*y^2) int(a,y) Результаты бега: a = 36*(x^2 + 4*x*y + 3*y^2 + 1)^(1/2) ans = 36*(x/3 + y/2)*(x^2 + 4*x*y + 3*y^2 + 1)^(1/2) - 2*3^(1/2)*log((x^2 + 4*x*y + 3*y^2 + 1)^(1/2) + (3^(1/2)*(2*x + 3*y))/3)*(x^2 - 3) >> 2. Аппроксимируйте с наименьшей среднеквадратической ошибкой полиномом произвольного порядка зависимость a sin(kx)+bcos(lx) y на интервале от 0 до 2π. Значения коэффициентов возьмите из табл. 4.2. Таблица 4.2
Формула для вычисления среднеквадратической ошибки для двух векторов x1 и x2 длиной n: 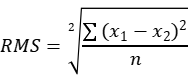 Код: syms x1 y1 y1=4*sin(2*x)+7*cos(1.6*x) x=1:0.1:6 y=4*sin(2*x)+7*cos(1.6*x) o=polyfit(x,y,8) x2=1:0.1:6 y2=polyval(o,x2) plot(x,y,x2,y2) y3=y-y2 frms=rms(y3) Результаты бега: 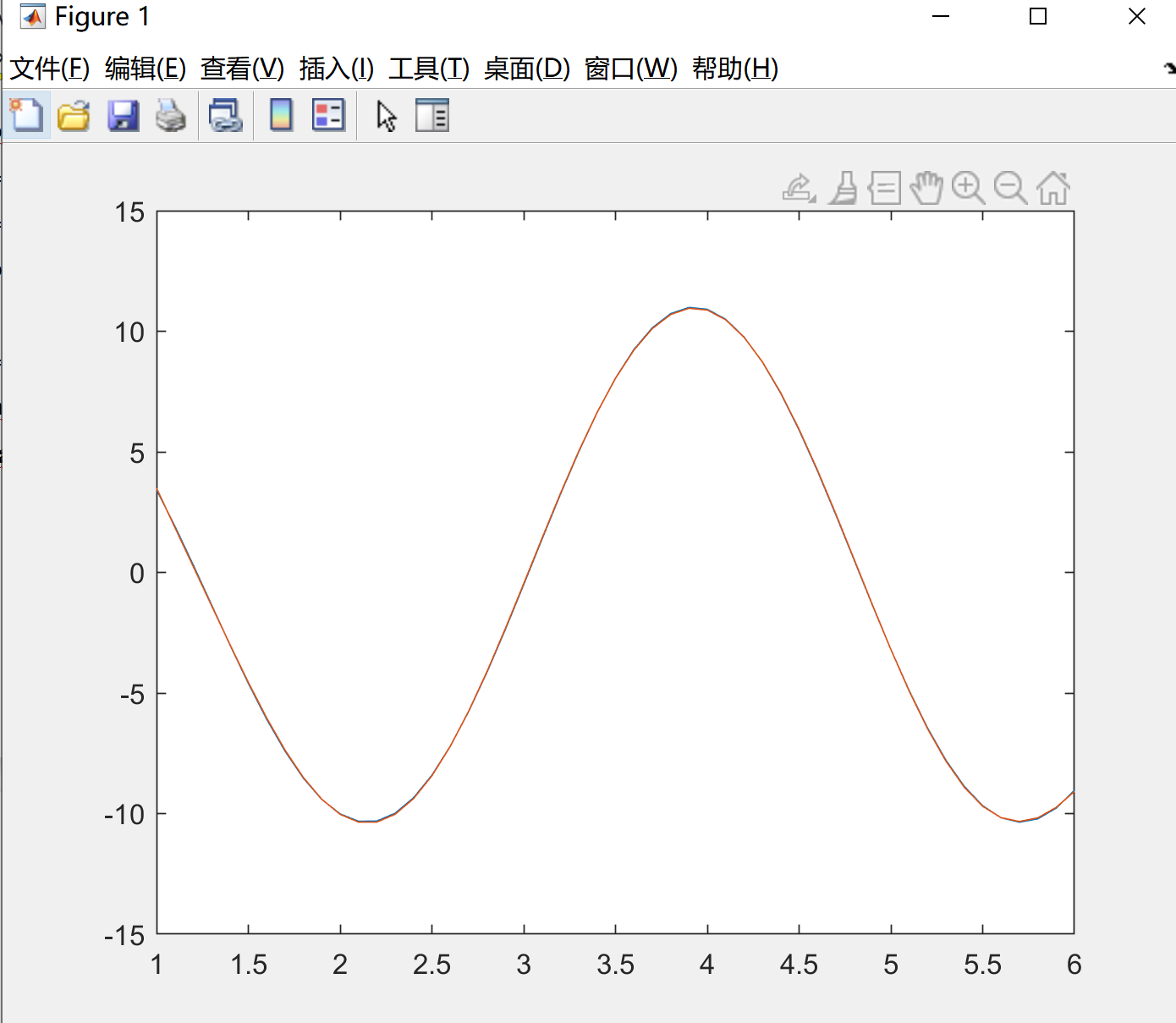 Рис 3 Результаты frms = 0.0304 Вывод: Научитесь использовать команду sym для вычисления различных функций и создания соответствующих изображений для получения результатов | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||