|
|
задания на построение сечений. Задания на построение сечений1. Как получить дополнительный балл при решении стереометрической задачи
«Школа успеха» по математике, 2019 г.
Задачи для подготовки к ЕГЭ (профильный уровень) по теме
«Как получить дополнительный балл при решении стереометрической задачи»
|
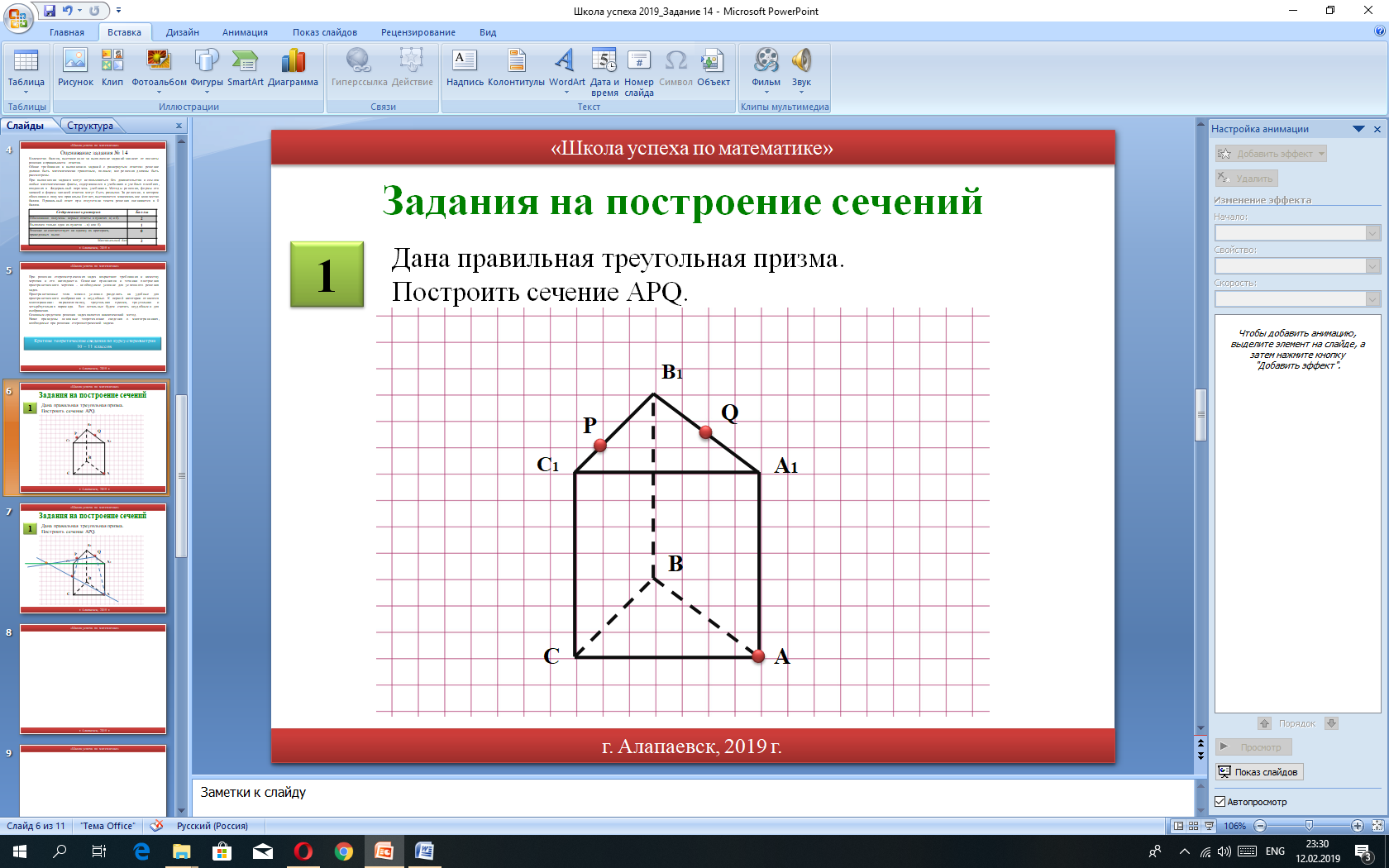
1
|
Дана правильная треугольная призма. Построить сечение APQ.
|
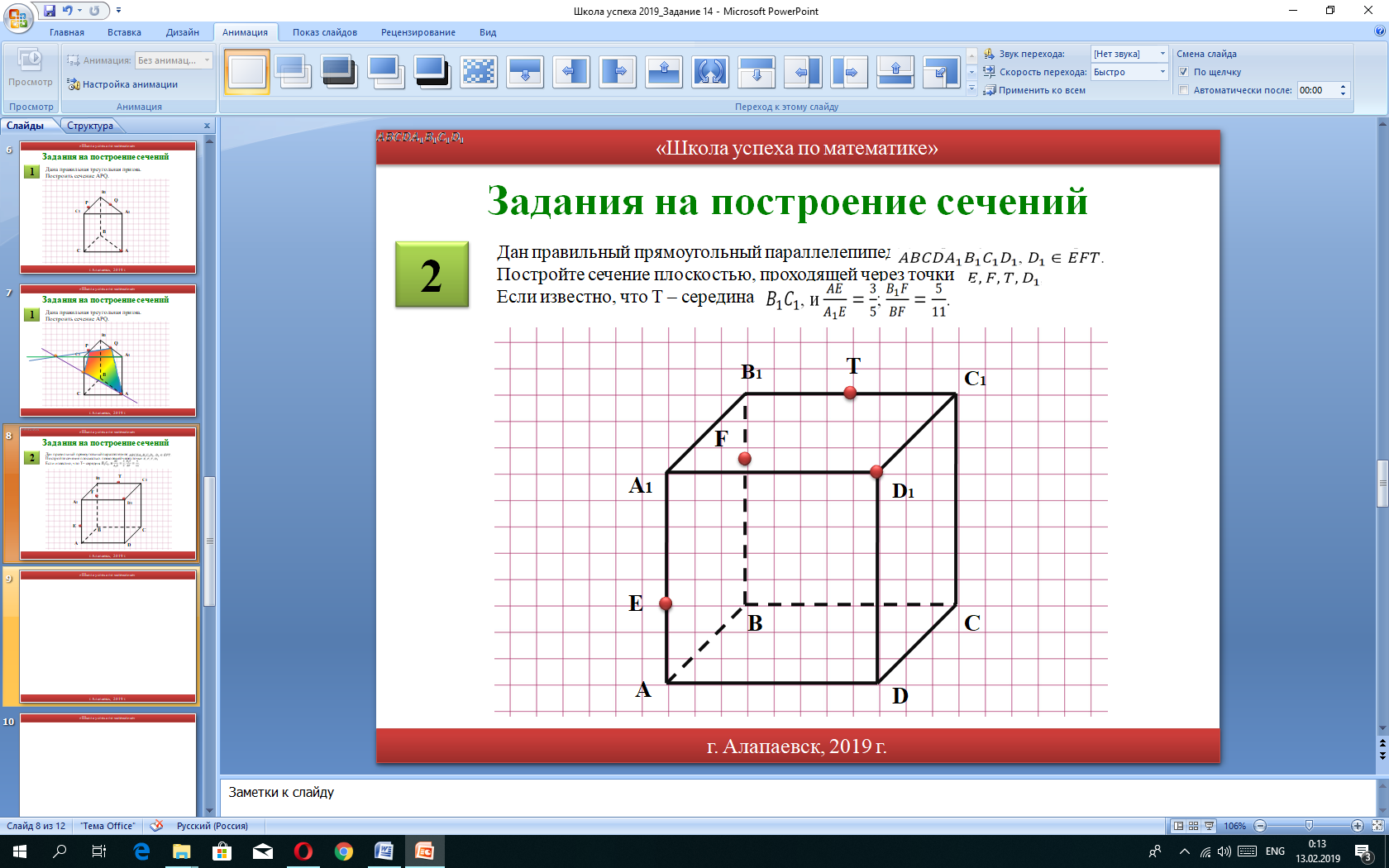
2
|
Дан правильный прямоугольный параллелепипед 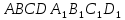 . Постройте сечение плоскостью, проходящей через точки . Постройте сечение плоскостью, проходящей через точки  и выяснить, принадлежит ли точка и выяснить, принадлежит ли точка  сечению EFT, если известно, что сечению EFT, если известно, что  - середина - середина  , и , и  ; ; 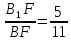 . .
|
|
|
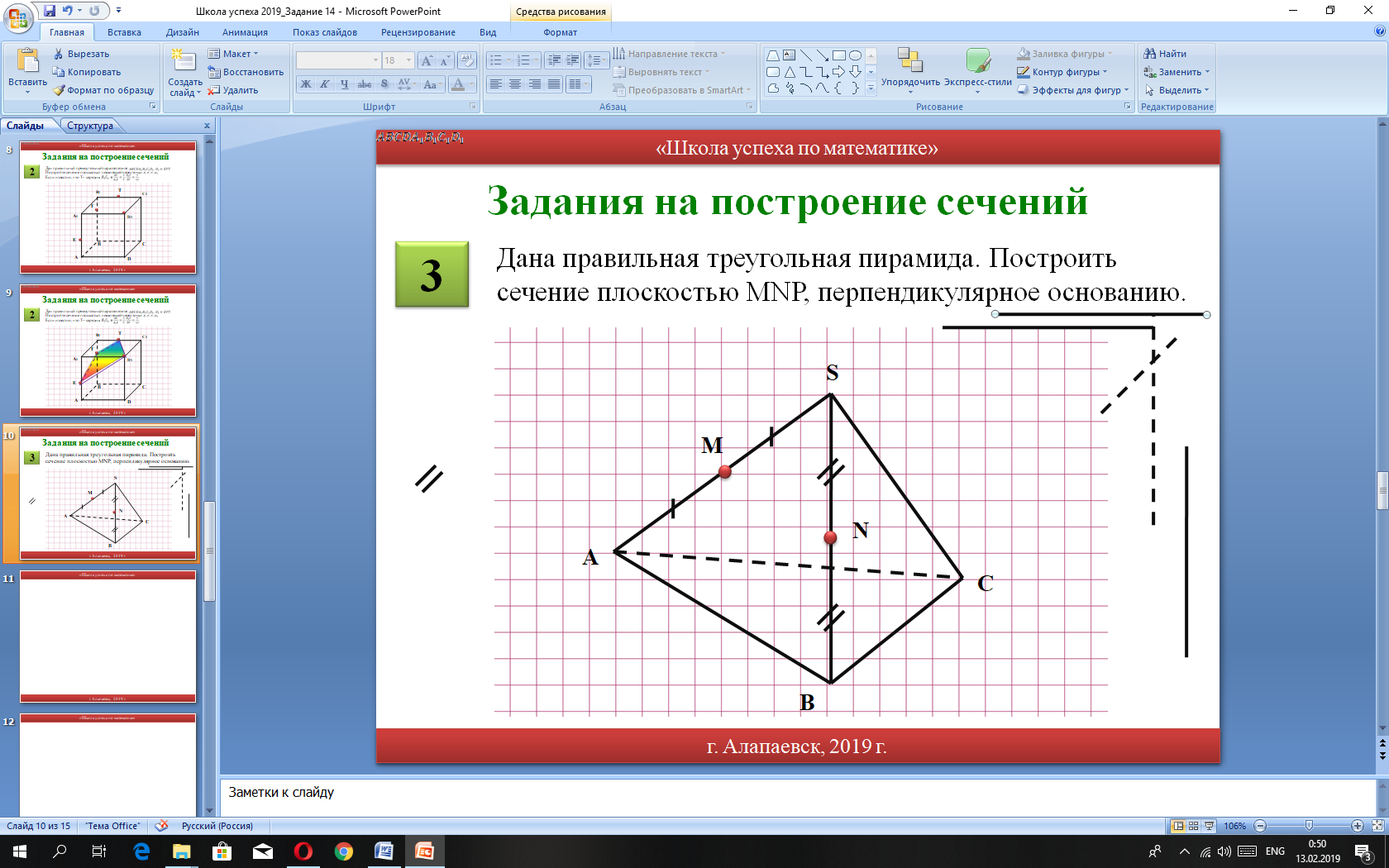
3
|
Дана правильная треугольная пирамида. Построить сечение плоскостью MNPQ, где P принадлежит BC и Q принадлежит AC, перпендикулярное основанию
|
4
|
Дан шар, построить сечение под углом 30° к осевому сечению.

|
|
|
Домашнее задание
|
1
|
Дана прямая призма. M – середина  , N – середина , N – середина  . Построить сечение . Построить сечение  . .

|
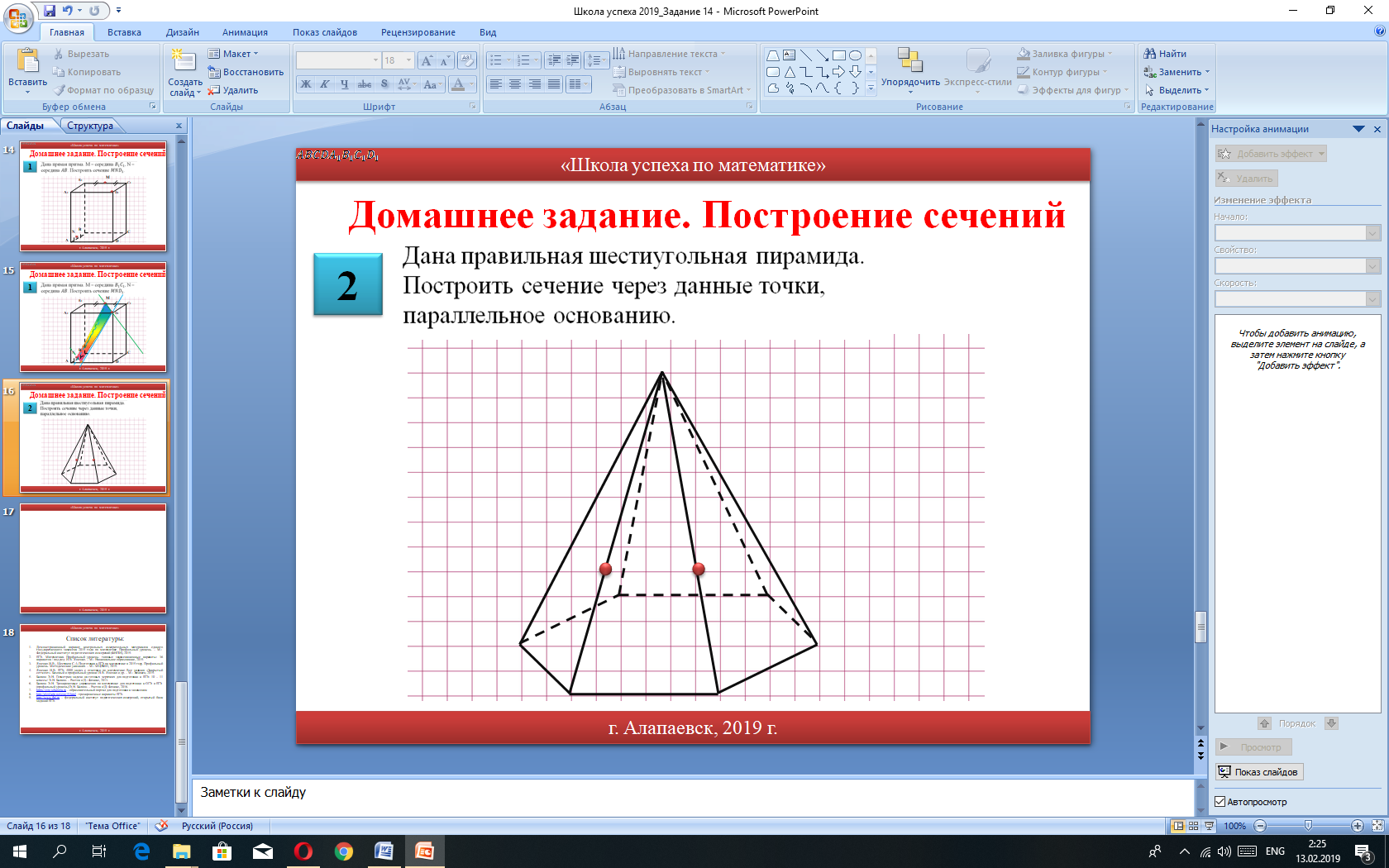
2
|
Дана правильная шестиугольная пирамида. Построить сечение через данные точки, параллельное основанию.
|
|
|
Задания № 14. Стереометрическая задача
1
|
Точка A, B,C лежат на окружности основания конуса с вершиной S, причём A и C диаметрально противоположные . Точка М середина ВС.
Докажите, что прямая SM образует с плоскостью ABC такой же угол, как и прямая AB с плоскостью SBC;
Найдите угол между прямой SA и плоскостью SBC, если AB = 2, BC = 4 и SC = 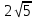 . .
|
2
|
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований выбраны точки А,В,С, а на окружности другого основания – точка С1, причём СС1 – образующая цилиндра, а АС – диаметр основания. Известно, что ∠АСВ = 450, АВ =3 , СС1 = 6. , СС1 = 6.
Докажите что угол между прямыми АС1 и ВС равен 600 .
Найдите расстояние от точки В до прямой АС1 .
|
3
|
На ребре SA правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка М, причём SM :MA = 5 : 1. Точки P и Q – середины рёбер BC и AD соответственно.
Докажите, что сечение пирамиды плоскостью MPQ является равнобедренной трапецией.
Найдите отношение объёмов многогранников, на которые плоскость MPQ разбивает пирамиду.
|
4
|
В правильной шестиугольной призме А…F1, все ребра которой равны 1, найти угол между плоскостями АВС и FBD1.
|
5
|
Задание из ФИПИ (демоверсия)
Все рёбра правильной треугольной призмы ABCA1B1C1 имеют длину 6. Точки M и N середины рёбер AA1 и A1C1 соответственно.
Докажите, что прямые BM и MN перпендикулярны.
Найдите угол между плоскостями BMN и ABB1 .
|
Домашнее задание
|
1
|
Точки А, В и С лежат на окружности основания конуса с вершиной S, причём А и С диаметрально противоположны. Точка М середина ВС.
Докажите, что прямая SM образует с плоскостью АВС такой же угол, как и прямая АВ с плоскостью SBC.
Найдите угол между прямой SA и плоскостью SBC, если АВ = 6, ВС = 8 и SC = 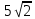 . .
ОТВЕТ: arcsin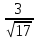
(Смотри решение задачи № 1)
|
2
|
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований выбраны точки А,В,С, а на окружности другого основания – точка С1, причём СС1 – образующая цилиндра, а АС – диаметр основания. Известно, что ∠АСВ = 300, АВ = , СС1 = , СС1 = 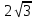 . .
Докажите что угол между прямыми АС1 и ВС равен 450 .
Найдите объём цилиндра.
ОТВЕТ: r =  , V = 12 , V = 12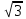 π π
(Смотри решение задачи № 2)
|
3
|
Точки А, В и С лежат на окружности основания конуса с вершиной S, причём А и С диаметрально противоположны. Точка М середина ВС.
Докажите, что прямая SM образует с плоскостью АВС такой же угол, как и прямая АВ с плоскостью SBC.
Найдите угол между прямой SA и плоскостью SBC, если АВ = 6, ВС = 10 и SC =  . .
ОТВЕТ : h =  . .
(Смотри решение задачи № 1)
|
4
|
На ребре SA правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка М, причём SM :MA = 1 : 2. Точки P и Q – середины рёбер BC и AD соответственно.
Докажите, что сечение пирамиды плоскостью MPQ является равнобедренной трапецией.
Найдите отношение объёмов многогранников, на которые плоскость MPQ разбивает пирамиду.
ОТВЕТ :  . .
(Смотри решение задачи № 3)
| |
|
|
 Скачать 1.88 Mb.
Скачать 1.88 Mb.