зачёт номер 3. зачёт 3. Карточка 1
 Скачать 128.58 Kb. Скачать 128.58 Kb.
|
|
Карточка 1. 1. Т. Площадь боковой поверхности призмы равна произведению периметра основания на высоту призмы. Sбок=Pосн*h Д 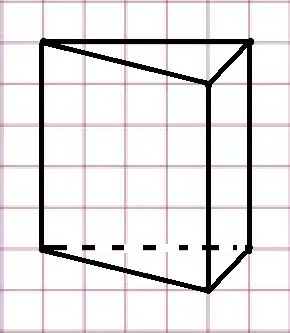 h a1 a2 a3 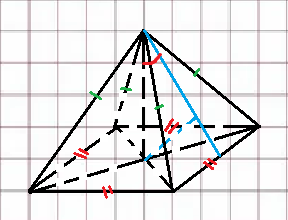 α S A D B C O K M -во: боковые грани прямоугольной призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте h призмы. Площадь боковой поверхности призмы равна сумме площадей указанных прямоугольников, т.е. равна сумме произведений сторон основания на высоту h. Вынося множитель n за скобки, получим в скобках сумму сторон основания призмы, т.е. его периметр P. Итак Sбок=Ph. 2. 305. Д 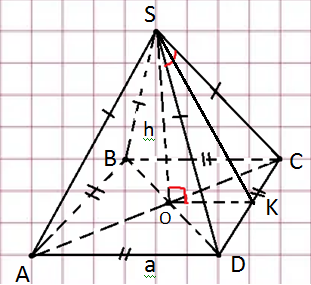 α  ано: SABCD – правильная пирамида, SO – высота = h, CSD =α ано: SABCD – правильная пирамида, SO – высота = h, CSD =α Найти: Sбок Решение: 1) тк SABCD - правильная пирамида, то SO – высота пирамиды, все боковые рёбра равны. Все боковые грани – равные треугольники (равны по 3 сторонам), тогда Sбок = 4* SDSC. Найдем SDSC. Для этого построим ОК DC. По т. о 3-ех перпендикулярах имеем SК DC 2 h ) SDSC = 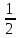 DC* SК. Пусть DA=a, DK=KC= DC* SК. Пусть DA=a, DK=KC=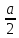 , тк SК-высота, а значит и медиана в равнобедренном DSC , тк SК-высота, а значит и медиана в равнобедренном DSC3 O K ) Из DSC имеем: 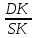 =tg =tg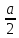 SК= DK* ctg 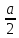 = = 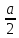 *ctg *ctg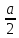 , ОК= , ОК=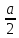 4) из прямоугольного SОК по т Пифагора имеем SО2+ОК2=SК2 h2+ 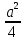 = = 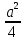 ctg2 ctg2 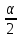 , a2= , a2= 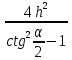 ctg2 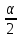 -1= -1=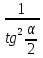 - 1= - 1=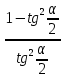 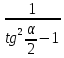 = =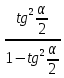 = =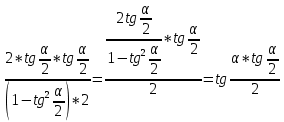 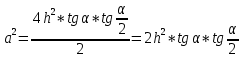 SDSC= 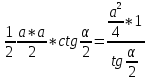 SDSC= 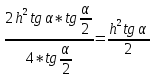 5) Sбок=4SDSC= 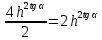 306. Дано: SABCD – правильная четырёхугольная пирамида, SO- высота=h, (SO;DSC) =α Найти: Sполн.поверх.пирамиды Решение: 1) тк SABCD – прав пирамида, SO-высота, то все боковые рёбра равны, все боковые грани – равные треугольники ( по трем сторонам) 2) построим OK⟂CD, соединим т.S и т. K. SO – высота, SK-наклонная, OK -проекция. SK⟂CD ( по т. о 3ёх перпенд.) построим в (SOK) OM⟂SK. SM-проекция SM на (DSC), значит ∠OSM -угол между прямой SO и (DSC)=α 3) из прямоугольного ∆SKO имеем SK= 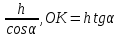 AD=CD=2OK=2htg 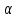 SDCS= 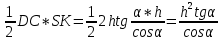 S 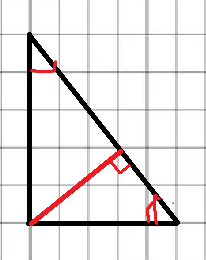 M S 90◦-α бок=4 SDCS=4* 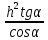 Sосн=SABCD=AD2= 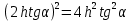 Sполн= Sбок+Sосн= 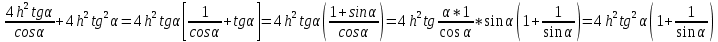 3. |
