Расчетно-Графическая работа. Решение1. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид

• Название: Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид
• Анкор: Расчетно-Графическая работа
• Дата: 15.05.2022
• Размер: 95 Kb.
• Имя файла: Решение1.doc
• Тип: Документы; #530156

Задание.

Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид: x(t) =

Найти:

1. 
   Среднюю скорость V_xср за интервал времени от t₁ до t₂; t₁=3c; t₂=8,4с;
   
2. 
   Среднюю путевую скорость V_ср за тот же интервал времени;
   
3. 
   Среднее ускорение.
   

Построить графики зависимостей х(t) и V_x(t).

Краткие теоретические сведения:

Материальная точка – это тело, размерами, которых можно пренебречь по сравнению с расстоянием до других тел.

Средней скоростью материальной точки в промежутке времени от t до t + t называется вектор (V), равный отношению пройденного пути за этот промежуток времени к его продолжительности t.

Ускорение – векторная физическая величина, характеризующая быстроту изменения скорости и равная первой производной от времени t от скорости V в этой точке.

Координата - это совокупность чисел или независимых переменных, которые определяют положение точки в пространстве.

Основные расчетные формулы:

При равнопеременном движении координата материальной точки по оси х имеет вид:

;

Скорость:



Производная координаты по времени есть скорость:

;

Средняя скорость, которой пройден путь S за интервал времени от t₁ до t₂:

;

Путевая скорость V за тот же промежуток времени:

;

При данном условии задачи ускорение остается постоянным: a = const.



Производная скорости по времени есть ускорение:

Расчеты:

1) S = x(t₁) – x(t₂);

x(t₁) = = (м);

x(t₂) = 78,4+2 = 81,38(м);

S = 33,6 -81,38= -47,78 (м);



2) Берем производную:

V(t) = ;

=7+43-0,6 = 13,6(м/с);

= = -1,736 (м/с);

Знак минус показывает, что тело движется в сторону противоположную направлению оси. В формулу подставляем по модулю.



3)

Так как движение у нас равнопеременное, то для проверки возьмем производную:

a = V(t) = ( ) = 4 -1,2t(м/с²)
Знак минус показывает, что движение равнозамедленное.

Графики.

График зависимости x(t): x(t) =7t+2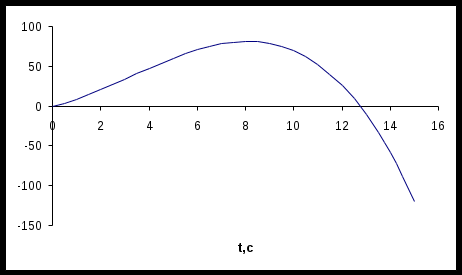

График зависимости a(t):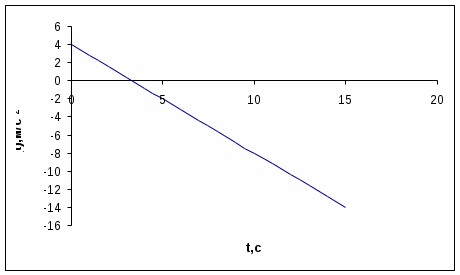

Окончательный ответ:

1)

2)

3) a = м/с².

Вывод.

В результате проделанной работы можно сказать, что при данном кинематическом уравнении движения материальной точки по прямой точка двигалась сначала равнозамедленно, затем остановилась и начала равноускоренное движение в обратную сторону. В расчетах были использованы основные физические формулы движения материальной точки по прямой и дифференцирование.