Кинематика точки. Линник (виправлення знову) (1). Кінематика точки
 Скачать 59.99 Kb. Скачать 59.99 Kb.
|
|
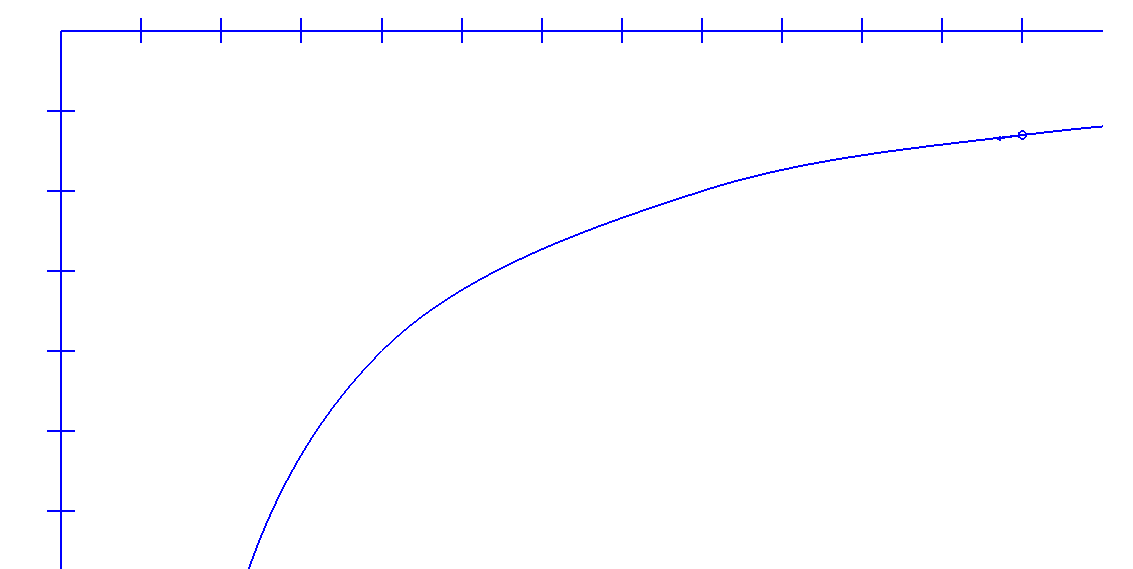
Міністерство освіти і науки України КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ БУДІВНИЦТВА І АРХІТЕКТУРИ Кафедра теоретичної механіки Розрахунково-графічна робота № 1 На тему : «Кінематика точки» Варіант №15 Виконала : студентка будівельного факультету групи ПЦБ 12с Линник Юлія Юріївна Перевірила: асистент Плохута Руслана Олександрівна Київ 2020 Варіант № 15 Дано: 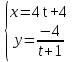 Знайти:y(x); v; a; aτ; an; ρ. Точка рухається у площині xy згідно з рівняннями: 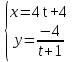 . .Визначити рівняння траєкторії точки; величину і напрям її швидкості; величину і напрям повного, дотичного, нормального прискорення і радіус кривизни для моменту часу t = 2c. Розв’язок: Для визначення рівняння траєкторії руху точки потрібно у рівняннях руху позбутися змінного параметру tта виразити залежність однієї координати через іншу. Перетворюємо рівняння руху: 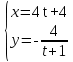 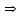 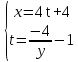 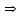 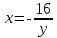 – це рівняння гіперболи,яка знаходиться в Ⅳ четверті. Початкова точка відліку при t0= 0 c; – це рівняння гіперболи,яка знаходиться в Ⅳ четверті. Початкова точка відліку при t0= 0 c; х0 = 4*0+4= 4 м; у0 = - 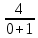 = -4м, тоді М0 (4;-4) = -4м, тоді М0 (4;-4)Будуємо дану гіперболу з відповідністю до рівняння (рис. 1.1.). Для визначення напрямку руху знаходимо початкове положення точки при t0 = 0 c на траєкторії та кінцеве при t1 = 2 c. Отримаємо: 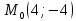 , , М1(12;-1,3). Зобразимо їх на траєкторії (рис. 1.2.). Рис. 1.1.
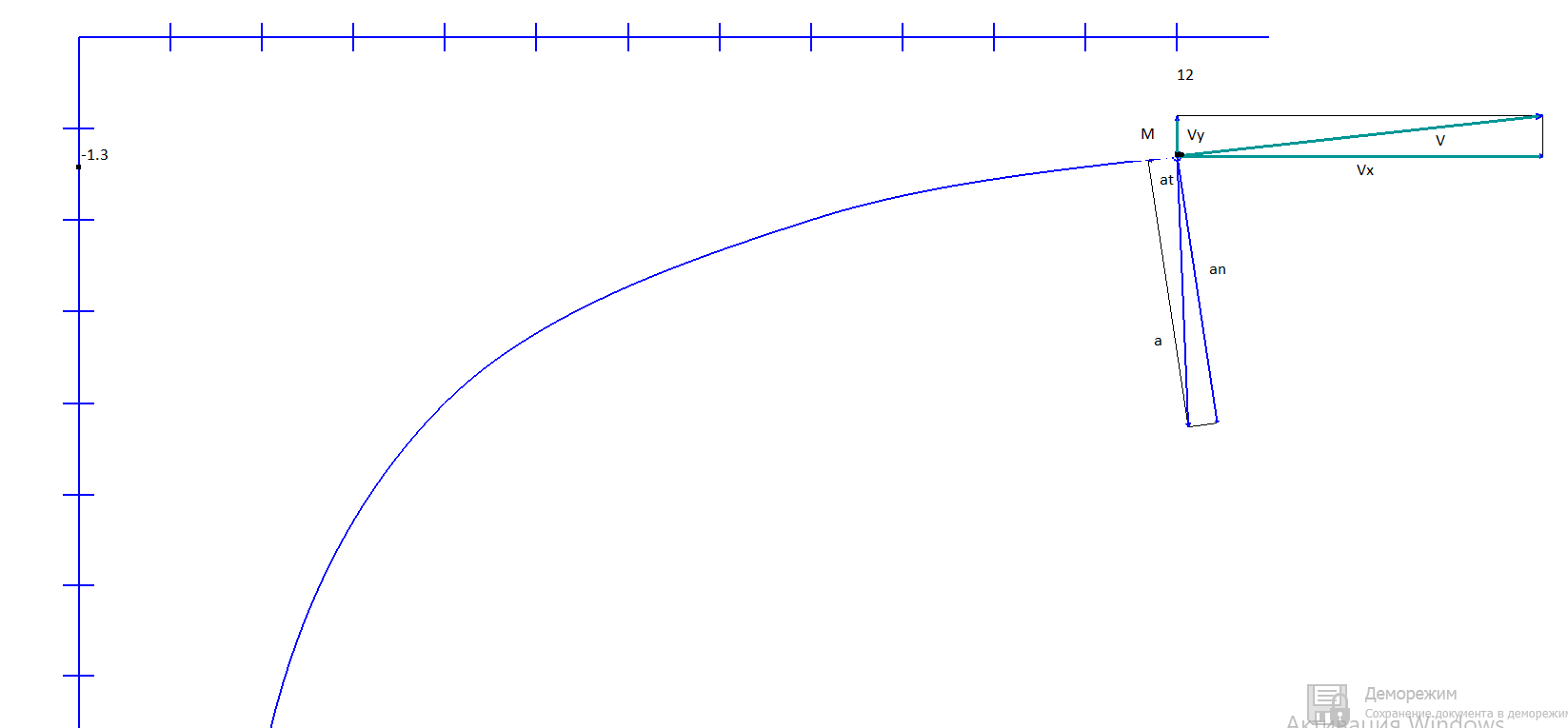
Для визначення швидкості точки візьмемо похідну за часом від рівнянь руху : 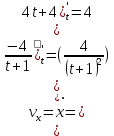 ; при t1 = 2 с ; при t1 = 2 с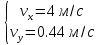 . .Проекції швидкості направлені паралельно відповідним осям. Вектор повної швидкості зображується за правилом паралелограма. Знайдемо повну швидкість точки: 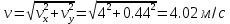 . .Для визначення прискорення візьмемо похідну за часом від рівнянь швидкості: 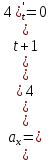 ; при t1 = 2 с ; при t1 = 2 с 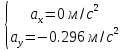 . .Зобразимо проекції прискорень паралельно відповідним осям з врахуванням знаків. Вектор повного прискорення точки будуємо за правилом паралелограма. Зображаємо вектори у масштабі.
Рис.1.4 Знайдемо значення повного прискорення точки: 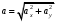 ; ;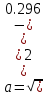 Так як, траєкторія руху точки – крива, то прискорення розкладається на складові : 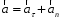 . .Для визначення тангенційного прискорення точки використаємо формулу: 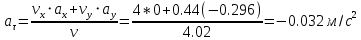 . .Дотичне прискорення спрямоване по дотичній до траєкторії руху точки в напрямку вектору повної швидкості (враховуючи знак «+»). Значення нормального прискорення знайдемо з формули: 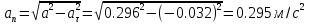 . .Вектор нормального прискорення направляємо перпендикулярно дотичному до центру кривизни. Визначимо радіус кривизни за формулою: 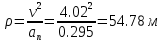 . .Відповідь: 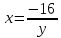 ; ; 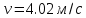 ; ; 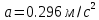 ; ; 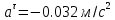 ; ; 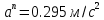 ; ; 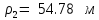 . . | ||||||||