Практика_2. Классы точности средств измерений
 Скачать 1.07 Mb. Скачать 1.07 Mb.
|
|
Практическая работа №2 Тема: классы точности средств измерений Учебная цель: - научиться определять классы точности средств измерений. Студент должен: уметь: - определять классы точности средств измерений знать: - определения прямых и косвенных измерений - какие систематические, прогрессирующие, абсолютные и относительные погрешности. - что такое основная и дополнительная погрешность прибора. Порядок выполнения работы 1. Повторить основные теоретические положения. 2.Рассчитать абсолютную и приведенную погрешность, определить приведенную относительную погрешность, определить какому классу точности соответствуют показания прибора. 3. Ответить на контрольные вопросы. Теоретический материал Мера — средство измерений в виде тела или устройства, предназначенного для воспроизведения величины одного или нескольких размеров, значения которых она содержит с необходимой для измерений точностью. Мерами являются, например, гири, мерные колбы, концевые меры длины. Мера позволяет воспроизвести величины, значения которых связаны с принятой единицей этой величины известным соотношением. Некоторые измерительные приборы могут применяться только с мерами. • По способу получения числового значения измеряемой величины все измерения подразделяют на четыре основные вида: прямые, косвенные, совокупные и совместные. Прямое измерение — это измерение, при котором искомое значение величины получают непосредственно от средства измерений: например, измерение длины линейкой, температуры — термометром, массы — взвешиванием и т. д. Косвенное измерение — определение искомого значения величины на основании результатов прямых измерений других величин, функционально связанных с искомой величиной. Совокупные измерения — одновременные измерения нескольких одноименных величин, при которых искомую величину определяют решением уравнений, получаемых при прямых измерениях различных сочетаний этих величин. Совместные измерения — одновременные измерения двух или нескольких разнородных (не одноименных) величин для нахождения зависимостей между ними. Под классом точности понимается обобщенная характеристика данного типа средств измерения, как правило, отражающая уровень их точности, выражаемая пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность. Общие положения деления средств измерений на классы точности установлены в ГОСТ 8.401 – 80 «Классы точности средств измерений». Основная погрешность средств измерений определяется погрешностью в нормальных условиях его применения. Дополнительная погрешность средств измерений – составляющая погрешности средств измерений, дополнительно возникающая из-за отклонения какой из влияющих величин (температуры и др.) от ее нормального значения. Погрешности измерений классифицируются по следующим признакам. По способу математического выражения погрешности делятся на абсолютные погрешности и относительные погрешности. - Абсолютная погрешность – это значение, вычисляемое как разность между значением величины, полученным в процессе измерений, и настоящим (действительным) значением данной величины. Абсолютная погрешность меры – это значение, вычисляемое как разность между числом, являющимся номинальным значением меры, и настоящим (действительным) значением воспроизводимой мерой величины. Значение погрешности измерения некоторой величины X принято характеризовать: - Относительная погрешность – это число, отражающее степень точности измерения. Относительная погрешность выражается в процентах. - Приведенная погрешность – это значение, вычисляемое как отношение значения абсолютной погрешности к нормирующему значению. - Систематической погрешностью называется составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же величины. При этом предполагается, что систематические погрешности представляют собой определенную функцию неслучайных факторов, состав которых зависит от физических, конструкционных и технологических особенностей средств измерений, условий их применения, а также индивидуальных качеств наблюдателя. Пределы допускаемой абсолютной основной погрешности устанавливают по формуле: Δ= ±a (1) или Δ =±(a+ bx) , (2) где Δ - пределы допускаемой абсолютной основной погрешности, выраженной в единицах измеряемой величины на входе (выходе) или условно в делениях шкалы; х - значение измеряемой величины на входе (выходе) средств измерений или число делений, отсчитанных по шкале; a, b - положительные числа, не зависящие от х. В обоснованных случаях пределы допускаемой абсолютной погрешности устанавливают по более сложной формуле или в виде графика либо таблицы. Пределы допускаемой приведенной основной погрешности следует устанавливать по формуле: 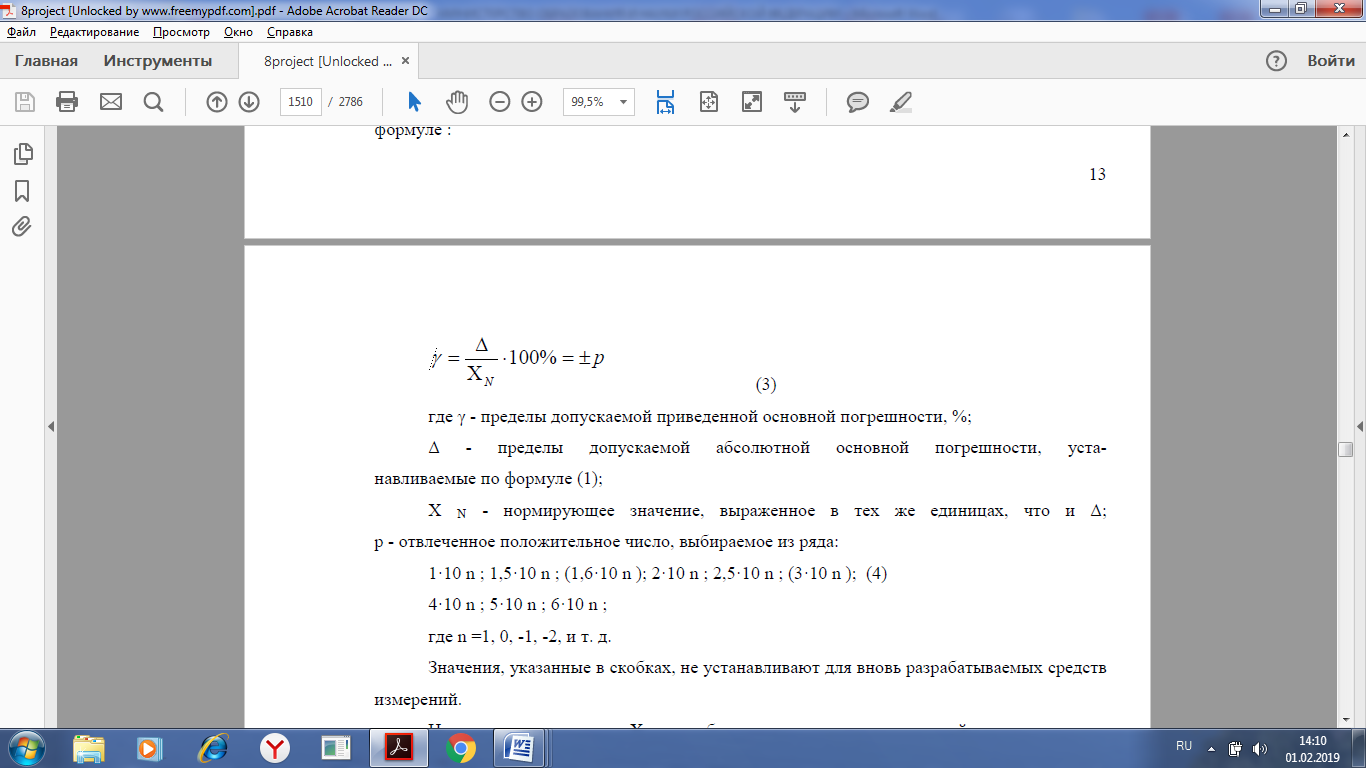 (3) (3)где γ - пределы допускаемой приведенной основной погрешности, %; Δ - пределы допускаемой абсолютной основной погрешности, устанавливаемые по формуле (1); XN - нормирующее значение, выраженное в тех же единицах, что и Δ; р - отвлеченное положительное число. Для измерительных приборов введено 8 классов точности: 0,05; 0,1; 0,5; 1,0; 1,5; 2,0; 2,5; 4. (4) Чем ближе измеряемая величина к номиналу, тем более точным будет результат измерения. Максимальная точность (т.е. наименьшая относительная ошибка), которую может обеспечить данный прибор, равна классу точности. Это обстоятельство необходимо учитывать при использовании многошкальных приборов. Шкалу надо выбирать с таким расчетом, чтобы измеряемая величина, оставаясь в пределах шкалы, была как можно ближе к номиналу. Если класс точности для прибора не указан, то необходимо руководствоваться следующими правилами: Абсолютная погрешность приборов с нониусом равна точности нониуса. Абсолютная погрешность приборов с фиксированным шагом стрелки равна Абсолютная погрешность цифровых приборов равна единице минимального разряда. Для всех остальных приборов абсолютная погрешность принимается равной половине цены деления. Нормирующее значение XN для большинства средств измерений определяется по формуле: XN = Xmax − Xmin, (5) где Xmax, Xmin – верхний и нижний предел шкалы измерительного средства. В ГОСТ 8.401 – 80 предусмотрены так же другие способы определения нормируемого значения (для приборов имеющих неравномерную шкалу, имеющих номинальное значение измеряемой величины и пр). Пределы допускаемой относительной основной погрешности устанавливают по формуле: 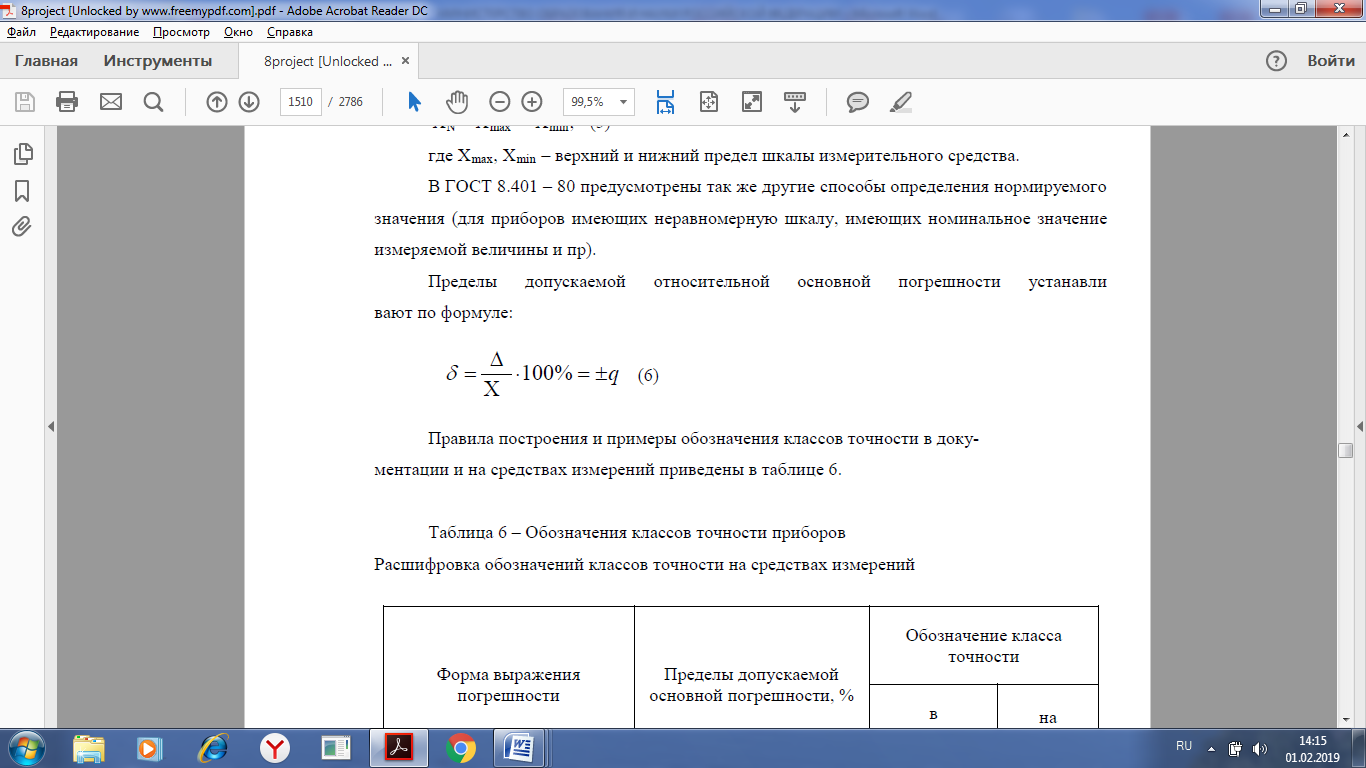 (6) (6)ЗАДАНИЕ Рассчитать абсолютную и приведенную погрешность по формулам (7) и (9), результат занести в таблицу 1. Название прибора, диапазон шкалы и результаты измерений взять из таблицы 2. По варианту. Абсолютная погрешность – определяется разницей между измеренным Хизм и истинным значением физической величины Хист Δ = Хизм – Xист (7) Абсолютной погрешностью – разностью между найденным на опыте (измеренным) Xизм и истинным значением Xист некоторой величины Абсолютная погрешность показывает, на сколько мы ошибаемся при измерении некоторой величины Х. Относительная погрешность определяется отношением абсолютной погрешности к истинному значению измеряемой величины, % 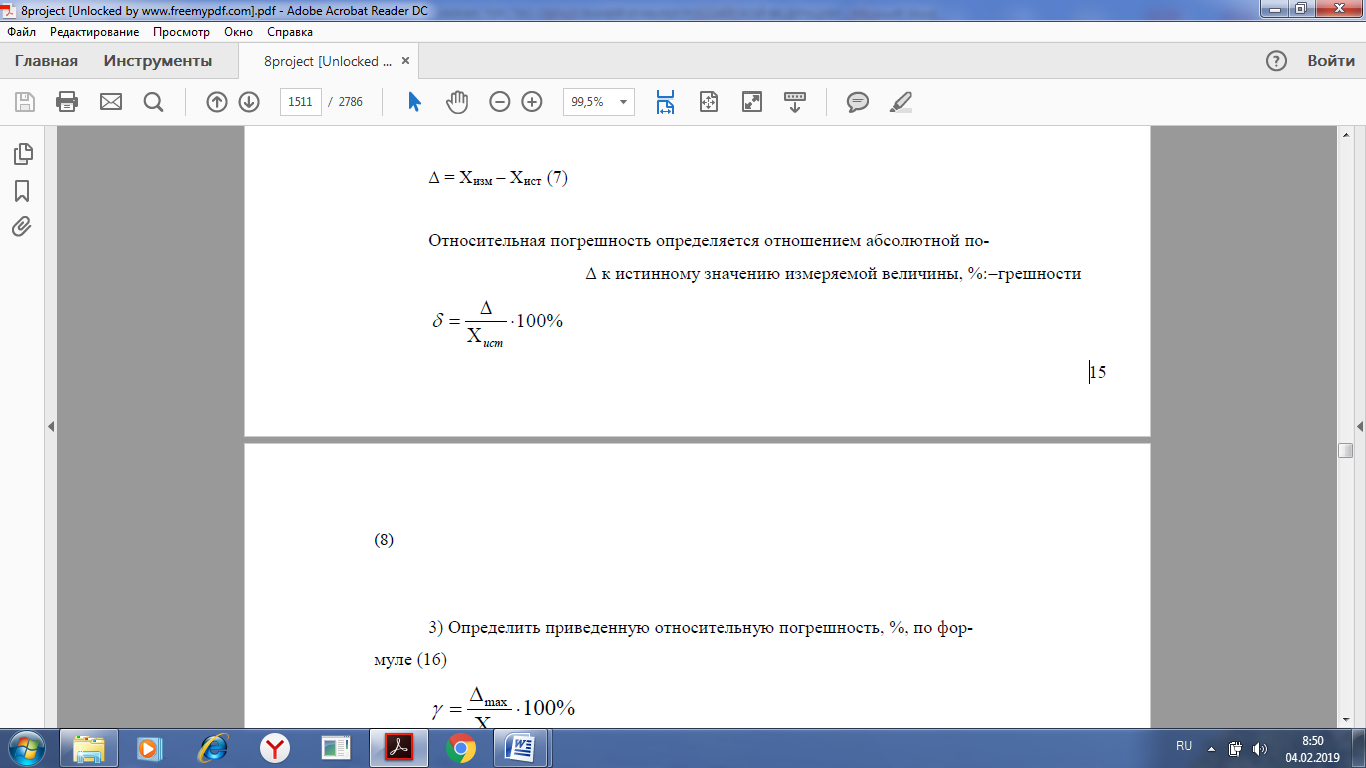 (8) (8)Относительная погрешность показывает, на какую долю от истинного значения величины Х мы ошибаемся. Определить приведенную относительную погрешность, %, по формуле (9) 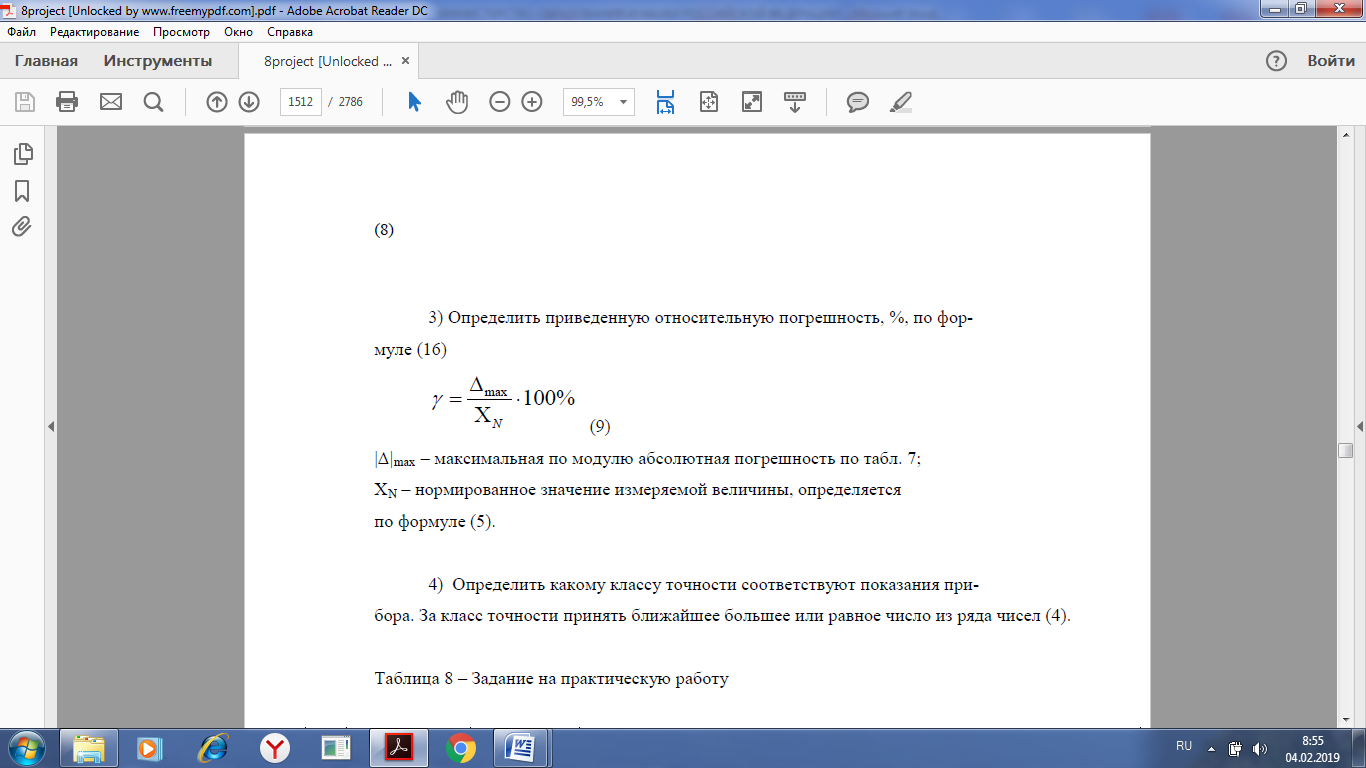 (9) (9)|Δ|max – максимальная по модулю абсолютная погрешность по таблице 1; XN – нормированное значение измеряемой величины, определяется по формуле (5). Определить какому классу точности соответствуют показания прибора. За класс точности принять ближайшее большее или равное число из ряда чисел (4). КОНТРОЛЬНЫЕ ВОПРОСЫ 1) Прямые и косвенные измерения. 2) Совокупные и совместные измерения 3) Систематические погрешности. 4) Основная погрешность прибора. 5) Абсолютные и относительные погрешности. 6) Дополнительная погрешность прибора. Таблица 1 - Расчет погрешностей измерений 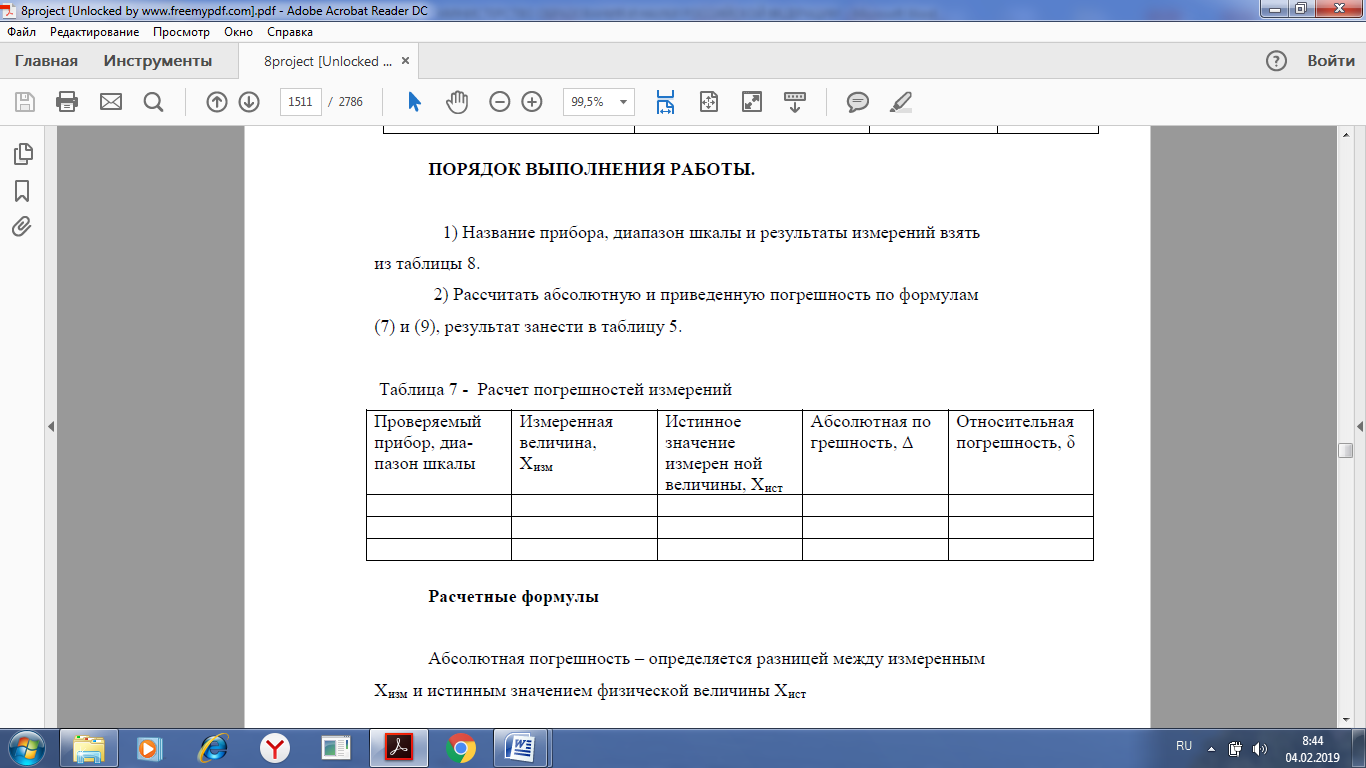 Таблица 2 - Варианты 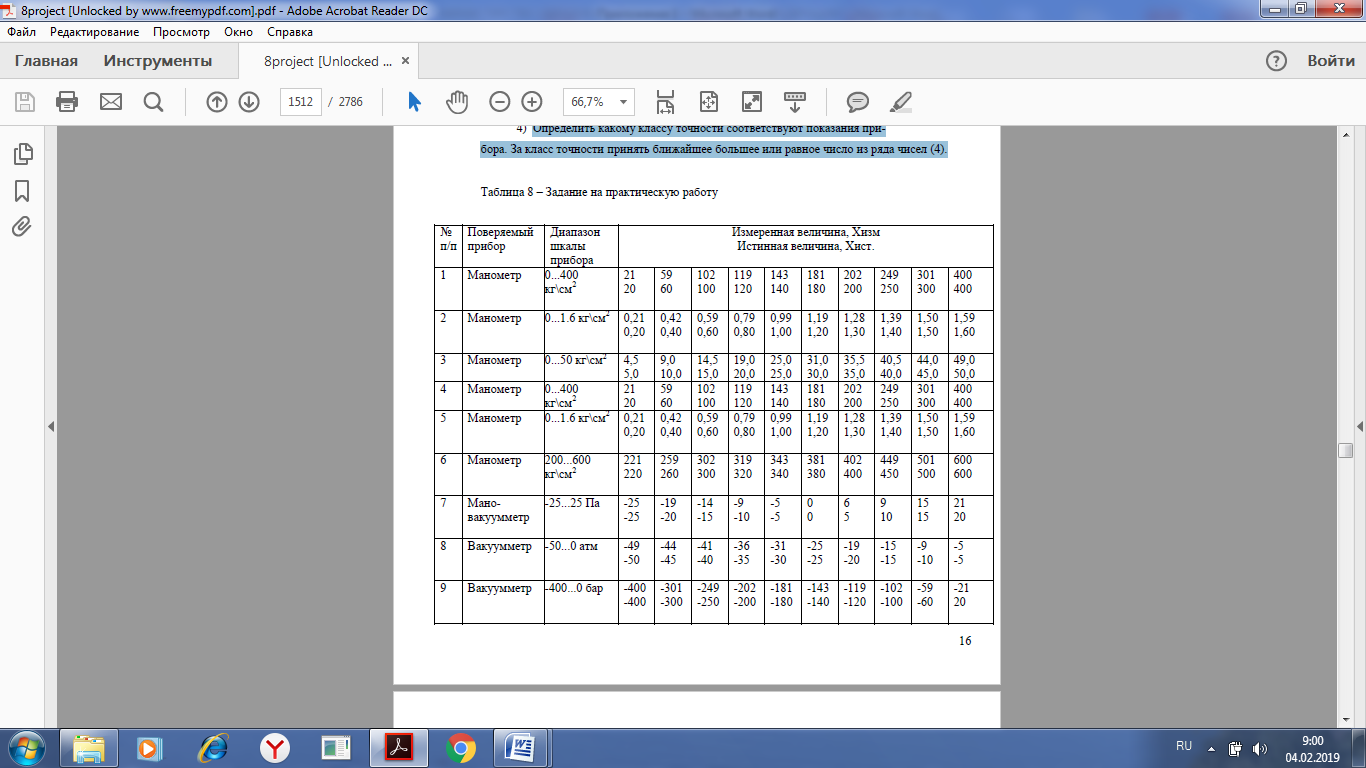  |
