квалиметия. Maple практика. Компьютерная математика и инженерное программирование

• Название: Компьютерная математика и инженерное программирование
• Анкор: квалиметия
• Дата: 17.03.2022
• Размер: 180.5 Kb.
• Имя файла: Maple практика.doc
• Тип: Документы; #401135

министерство образования и науки российской федерации

Федеральное государственное бюджетное образовательное учреждение высшего

образования

«Тихоокеанский государственный университет»

Кафедра «Технологическая информатика и информационные системы»
Maple практика

на тему «Компьютерная математика и инженерное программирование»

Вариант № 1

Номер группы: ОНГ (аб)зу-91

Выполнил: студент Ашуров Х. М.

Номер зачетной книжки: 190014001

Проверил: ____________________
Хабаровск, 2021

Задание 1. Векторы и матрицы.

а) Даны два вектора. Найти сумму этих векторов, скалярное и векторное произведение, угол между ними и длину векторов.

a(0, 5, 3); b(1, 2, 8)

б) Дана система линейных уравнений. Записать систему уравнений в матричной форме: АХ = В.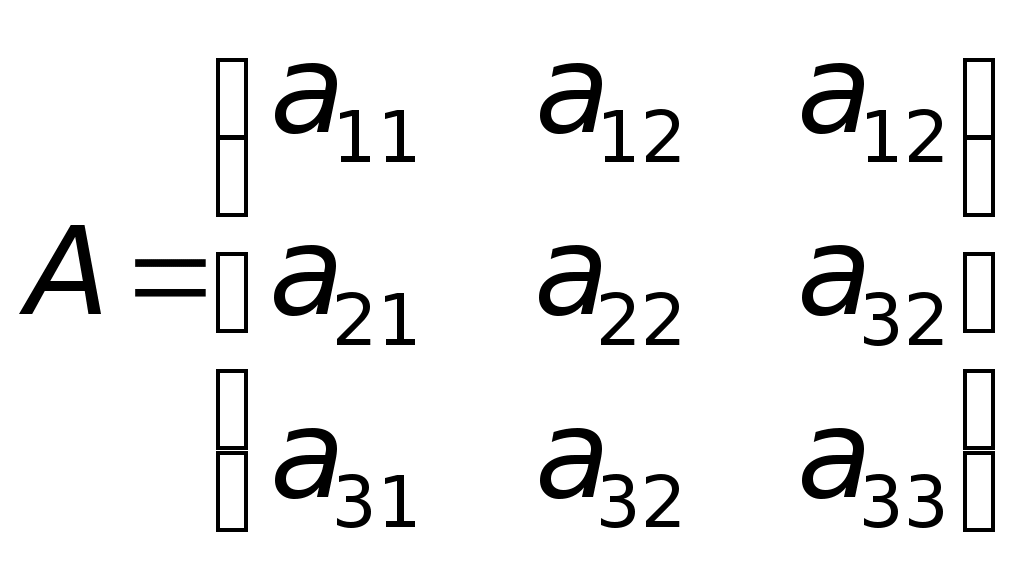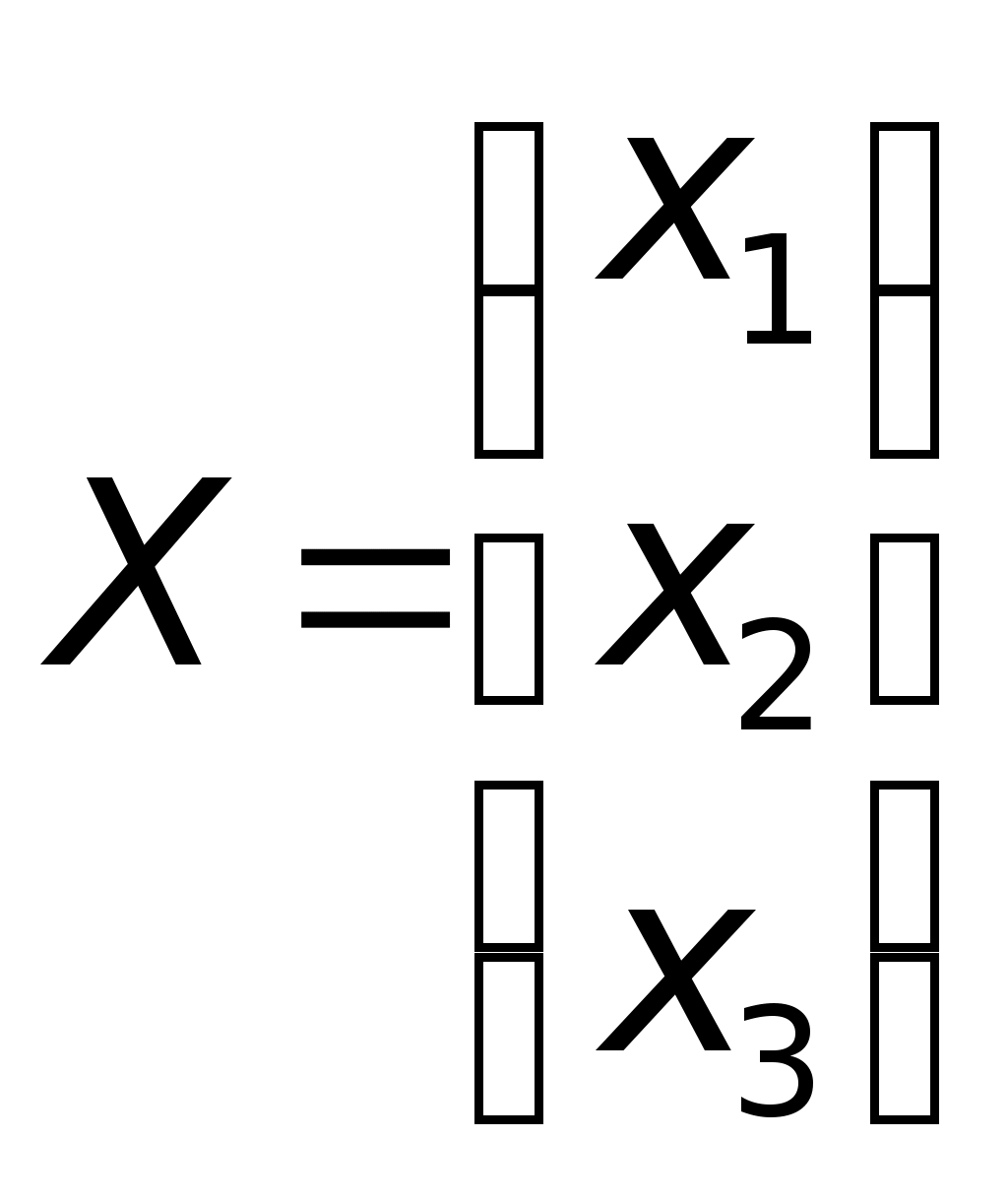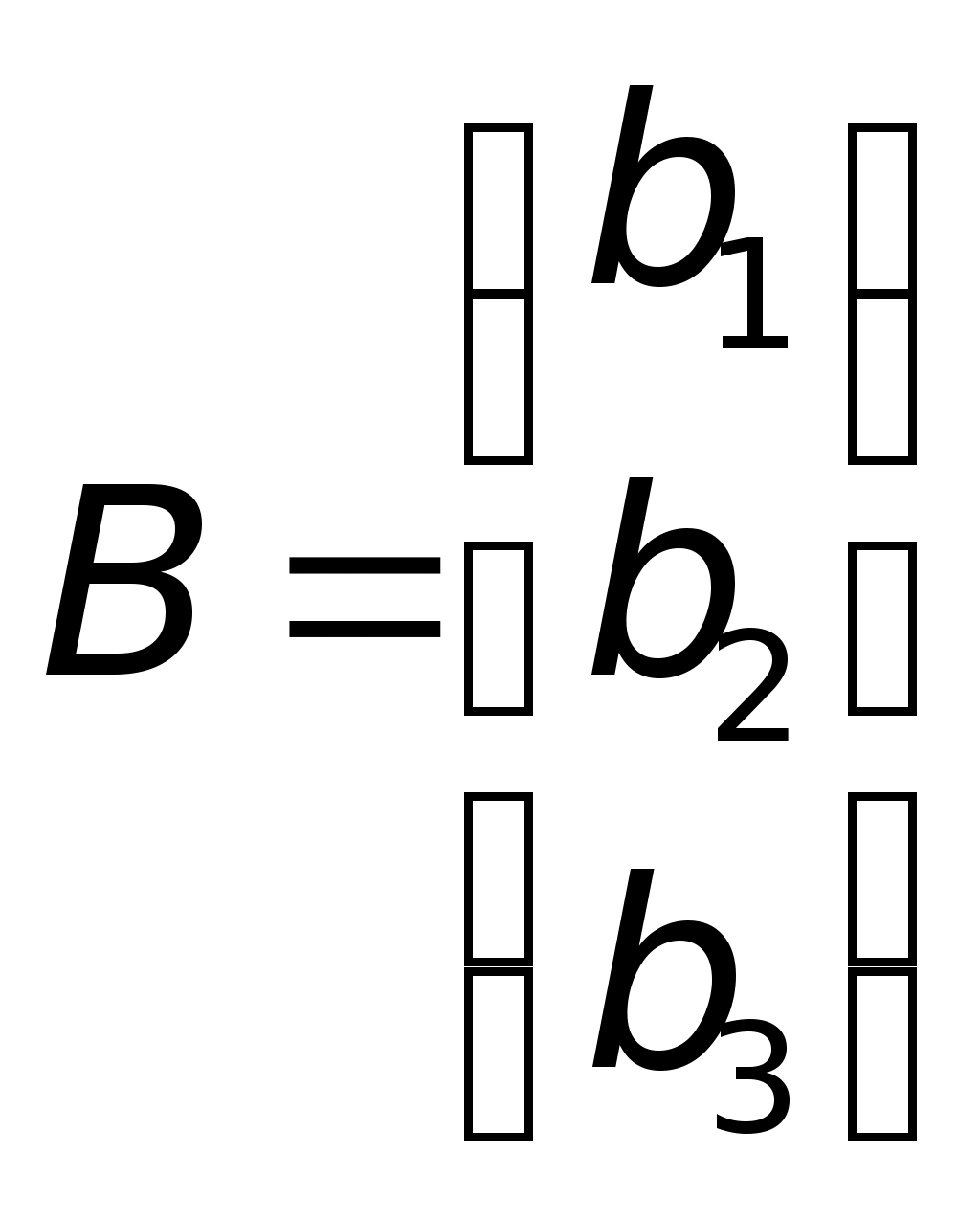

, ,

Найти определитель матрицы А и миноры. Записать матрицу, обратную матрице А и произвести проверку: АА^-1 = Е (где Е – единичная матрица). Найти матрицу X по формуле: X = А^-1В.

3x₁ + 2x₂ – 5x₃ = 10

7x₁ + 3x₂ – x₃ = 2

x₁ + 2x₂ – 8x₃ = 4

Решение: а) Подключаем библиотеку linalg и определяем векторы:



Находим сумму векторов, скалярное и векторное произведение, угол между ними и длину векторов.



б) Определяем матрицы A, B и X:



Находим определитель матрицы А и миноры.



Вычисляем обратную матрицу: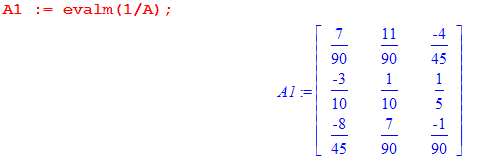



Выполняем проверку: АА^-1 = Е (где Е – единичная матрица).



Находим матрицу X по формуле: X = А^-1В:



Задание 2. Пределы.

Вычислить пределы функции f(x). Найти предел справа и слева от точки х.



Решение: Вычислим предел функции f(x), а также пределы справа и слева от точки х:



Задание 3. Производные.

а) Найти производную f (x) функции f(x) и затем проинтегрировать ее.



б) Найти первые и вторые производные f(х, у) по x; f(х, у) по у; f(х, у) по х;

f(x, y) по у.



Решение: а) Находим производную f (x) функции f(x) и затем проинтегрируем ее.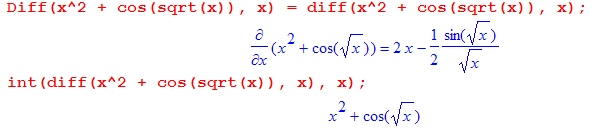



б) Определяем функцию f(x,y) и находим производные: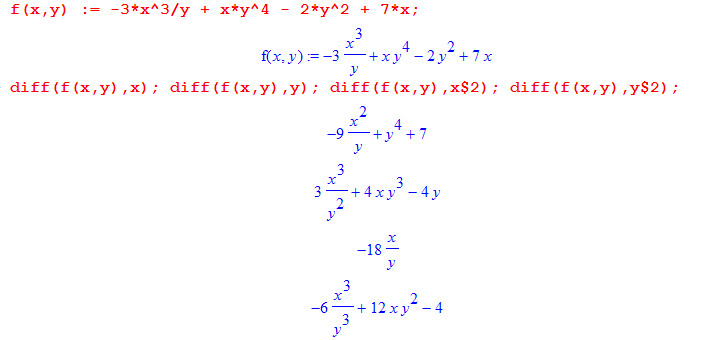



Задание 4. Решить уравнение

а) нелинейное уравнение



б) тригонометрическое уравнение



Решение: а) Для решения уравнения применяем функцию solve:



б) Для получения всех решений тригонометрического уравнения определяем константу _EnvAllSolutions и применяем функцию solve.



Задание 5. Построить графики:

а) кривую, заданную параметрически. Задать толщину линий 2, цвет зеленый.

sin(3t), cos(5t), t = 0..2

б) кривую в полярной системе координат. Задать стиль линий – точки, стиль символа – ромб, цвет – синий.

 = 1 – sin(t), t = 0..2

Решение: а) Построим кривую sin(3t), cos(5t), x = 0..2, заданную параметрически. Толщину линий задаем с помощью опции thickness, цвет задаем с помощью опции color: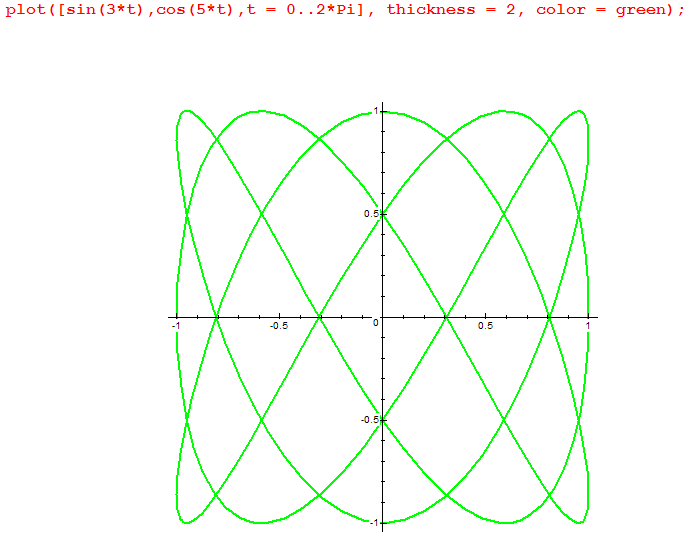



б) Построим кривую  = 1 – sin(t), t = 0..2, заданную в полярной системе координат. Стиль линий задаем с помощью опции style, цвет задаем с помощью опции color, стиль символа задаем с помощью опции symbol.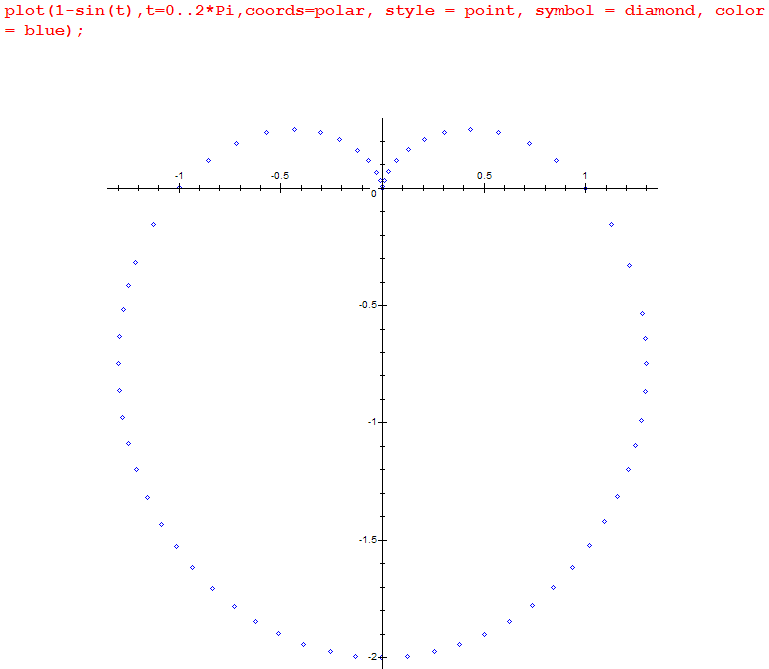



Примечание: Решения получены с помощью математического пакета Maple V Release 4.