Комплекс сандар рісі. Комплекс сандара амалдар олдану. Комплекс сандарды тригонометриялы формасы
 Скачать 147.45 Kb. Скачать 147.45 Kb.
|
|
Комплекс сандар өрісі. Комплекс сандарға амалдар қолдану. Комплекс сандардың тригонометриялық формасы. Жоспар. Комплекс сандар туралы түсінік Комплекс сандарға амалдар қолдану. Комплекс саннан түбір табу және дәрежеге шығару. 1. Комплекс сандар туралы түсiнiк Анықтама. Реттелген нақты сандар жұбы (x,y) комплекс сандар деп аталады және былай белгiленедi: 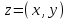 . .Мұнда х пен y нақты сандарын комплекс санның нақты және жорамал бөлiктерi деп атайды да, мына 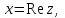 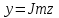 символдарымен белгiлейдi. Сонда символдарымен белгiлейдi. Сонда 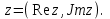 Oxy координаталар жазықтығында комплекс сан 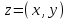 -тiң геометриялық бейнесi нүкте М(х,у) не вектор -тiң геометриялық бейнесi нүкте М(х,у) не вектор 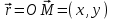 болады. Комплекс сандар жиыны мен Oxy жазықтығының нүктелерi арасында бiрмәндi сәйкестiк болатындығы дәлелденген. Сондықтан да Оxy - ты шартты түрде комплекс жазықтық деп атайды. болады. Комплекс сандар жиыны мен Oxy жазықтығының нүктелерi арасында бiрмәндi сәйкестiк болатындығы дәлелденген. Сондықтан да Оxy - ты шартты түрде комплекс жазықтық деп атайды. Жорамал бөлiгiнiң таңбалары қарама-қарсы болып келген екi комплекс сан 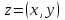 және және 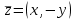 түйiндес сандар деп аталады. түйiндес сандар деп аталады. 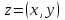 комплекс санын бейнелейтiн нүктенiң полярлық координаттары комплекс санын бейнелейтiн нүктенiң полярлық координаттары 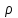 және және 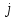 болсын дей отырып келесi түсiнiктердi ендiрелiк (2-cурет). болсын дей отырып келесi түсiнiктердi ендiрелiк (2-cурет).Анықтама. 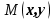 нүктесiнiң полярлық радиусы нүктесiнiң полярлық радиусы 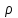 -ны -ны 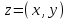 комплекс санының модулi деп атайды және былай белгiленедi комплекс санының модулi деп атайды және былай белгiленедi 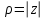 . . Демек, 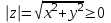 . Онда . Онда 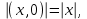 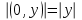 болады. болады.
Мына теңсiздiктi 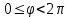 қанағаттандыратын қанағаттандыратын 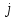 мәндерiн комплекс санның бас мәнi деп атап, мәндерiн комплекс санның бас мәнi деп атап, 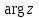 деп белгiлейдi.Егер деп белгiлейдi.Егер 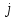 мына аралықта мына аралықта 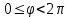 өзгерсе, онда өзгерсе, онда
болады . (0.1) түрiндегi комплекс сан жорамал бiрлiк деп аталып, i символымен белгiленедi. Демек, 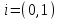 , , 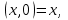 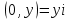 болатындығын ескерсек, онда кез келген комплекс санды былай жазамыз болатындығын ескерсек, онда кез келген комплекс санды былай жазамыз 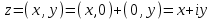 . .Комплекс санның мына түрде 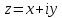 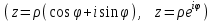 жазылуын, оның алгебралық (тригонометриялық, көрсеткiштiк) түрлерде жазылуы деп атайды. 2. Комплекс сандарға амалдар қолдану. 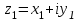 және және 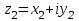 комплекс сандары берiлсiн. комплекс сандары берiлсiн. 1. 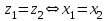 және және 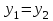 . .2. 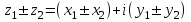 . .3. 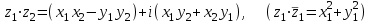 . .Демек, алгебралық түрде жазылған комплекс сандарды қосу мен көбейту көпмүшелiктердi қосу мен көбейту сияқты орындалады, тек қана 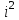 -ын (-1) санымен алмастыру керек. -ын (-1) санымен алмастыру керек.4. 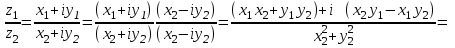 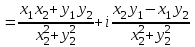 . .Алгебралық түрде жазылған комплекс сандарды бөлу үшiн, бөлшектiң алымы мен бөлiмiн бөлiмiнiң түйiндесiне көбейтiп, оның нақты және жорамал бөлiктерiн анықтау керек, яғни бөлiмiн жорамалдықтан құтқару керек. Егер комплекс сандар тригонометриялық (көрсеткiштiк) түрде 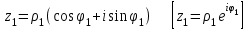 , , 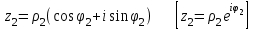 берiлсе, онда көбейту мен бөлу келесi формулалар бойынша ықшамды орындалады: 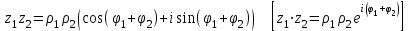  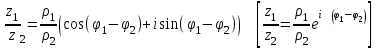 . .3. Комплекс саннан түбір табу және дәрежеге шығару. Комплекс сан 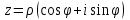 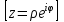 берiлсе, онда берiлсе, онда 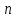 дәрежеге шығару мен дәрежеге шығару мен 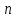 дәрежелi түбiр табу төмендегi формулаларға негiзделген ( дәрежелi түбiр табу төмендегi формулаларға негiзделген (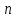 натурал сан): натурал сан): 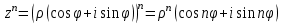 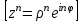 , ,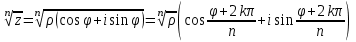 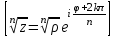 (*) (*)Мұндағы 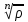 арифметикалық түбiр және арифметикалық түбiр және 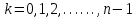 мәндерiн қабылдайды . мәндерiн қабылдайды .Мысал. 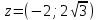 cанын комплекс жазықтықта бейнелеп, оның алгебралық, тригонометриялық және көрсеткiштiк түрде жазып және cанын комплекс жазықтықта бейнелеп, оның алгебралық, тригонометриялық және көрсеткiштiк түрде жазып және 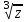 есептеп, бейнесiн табу керек. есептеп, бейнесiн табу керек.Шешуi: Мұнда 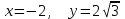 . Берiлген комплекс санның бейнесi M-нүктесi болады (3-cурет) және модулi мен аргументi былай анықталады: . Берiлген комплекс санның бейнесi M-нүктесi болады (3-cурет) және модулi мен аргументi былай анықталады: 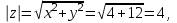 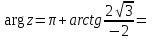
 Сонда Сонда 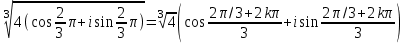 , , 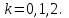 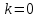 болғанда, болғанда,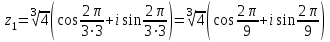 , , 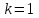 болғанда, болғанда, 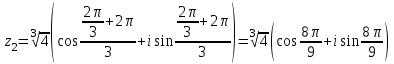 , , 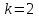 болғанда, болғанда, 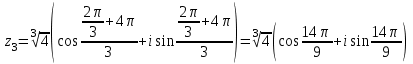 . .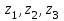 түбiрлерi 24-суретте бейнеленген . түбiрлерi 24-суретте бейнеленген .Мысал. 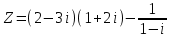 комплекс санының Rez және Jmz бөлiктерiн табу керек. комплекс санының Rez және Jmz бөлiктерiн табу керек.Шешуi: Көрсетiлген амалдарды орындаймыз: 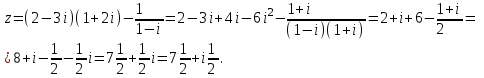 Демек, 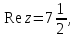 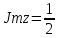 . .Бақылау сұрақтары. 1. Комплекс сан дегеніміз қандай сан? 2. Комплекс сандарға қандай негізгі амалдарды қолдануға болады? 3. Комплекс санды дәрежеге шығару қалай орындалады? 4. Комплекс саннан түбір табу? ҰСЫНЫЛҒАН ӘДЕБИЕТТЕР Әжібеков Қ., Әшірбаев Н., Каратаев Ж. Жоғары математика есептері мен жаттығулары. Шымкент, ОҚМУ, 2005-27 бет Әшірбаев Н.Қ., Сұлтанбек Т.С., Каратаев Ж. Жоғары математика тест тапсырмалары. Шымкент, ОҚМУ, 2006-201 бет. Көпеш Б., Әшірбаев Н.Қ. Жоғары математика курсының негіздері. Шымкент, ҚККА, 2005-283 бет. Әшірбаев Н.,Дуйсебаева П.,Сұлтанбек. Т.,Қаратаев Ж.. Сызықты алгебра және аналитикалық геометрия есептері мен жаттығулары.Шымкент 2007. Хасеинов К.А. Математика канондары.Алматы-2004,691 бет. Минорский В.С. Сборник задач по высшей математике. М., «Наука», 1977. |

 у
у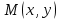 нүктесiнiң полярлық бұрышы
нүктесiнiң полярлық бұрышы 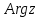 , яғни
, яғни 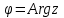 . Полярлық бұрыштың бiрмәндi анықталмайтындығы белгiлi (
. Полярлық бұрыштың бiрмәндi анықталмайтындығы белгiлi ( ) (қосындысына дейiнгi дәлдiкпен анықталады), сондықтан да комплекс санның аргументi де бiрмәндi анықталмайды.
) (қосындысына дейiнгi дәлдiкпен анықталады), сондықтан да комплекс санның аргументi де бiрмәндi анықталмайды.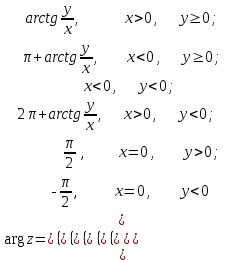
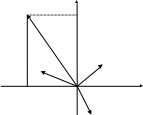 у
у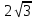
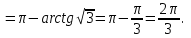
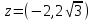 санының алгебралық, тригонометриялық және көрсеткiштiк түрлерi былай болады:
санының алгебралық, тригонометриялық және көрсеткiштiк түрлерi былай болады: 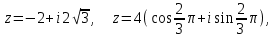
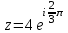 .
.